钢筋混凝土箱型墩的双向恢复力特性

夏樟华　 宗周红

(1福州大学土木工程学院, 福州350108)(2东南大学土木工程学院, 南京210096)



钢筋混凝土箱型墩的双向恢复力特性

夏樟华1宗周红2

(1福州大学土木工程学院, 福州350108)(2东南大学土木工程学院, 南京210096)

为了建立钢筋混凝土箱型墩在双向地震作用下弹塑性响应的简化分析模型,对其在双向反复荷载作用下的荷载-位移恢复力特性进行了研究.首先介绍了钢筋混凝土箱型墩双向拟静力试验的基本情况及其破坏模式.其次,结合双向压弯作用下钢筋混凝土箱型截面的弯矩曲率分析,建立了箱型墩构件峰值位移、极限位移和残余变形的计算方法,并提出了钢筋混凝土箱型墩荷载-位移三折线骨架曲线和卸载刚度的计算公式,建立了相应的理论恢复力模型.最后,利用试验结果,对理论恢复力模型进行分析和验证.结果表明,钢筋混凝土箱型墩在双向荷载作用下以弯曲破坏为主,实测和计算骨架曲线、滞回曲线吻合良好,考虑双向荷载作用的理论恢复力模型能够反映钢筋混凝土箱型墩的基本抗震性能.

钢筋混凝土箱型墩;双向拟静力试验;残余变形;骨架曲线;滞回曲线

钢筋混凝土箱型墩在桥梁结构中得到了越来越多的应用,但其抗震性能的研究大都基于单向拟静力试验[1-5],多向荷载作用下的箱型墩抗震性能试验研究较少[6-7],基本没有涉及到恢复力特性的研究.因此,有必要研究考虑多向荷载作用的钢筋混凝土箱型墩恢复力特性.目前建立考虑多向荷载作用恢复力模型的方法有2种：① 按照经典弹塑性理论,将单轴应力应变关系扩展到多轴应力应变关系,这种方法比较复杂[8-10].② 利用纤维模型,将截面细化为若干纤维单元，并由各个截面中纤维的应力应变关系计算得到对应截面的力与变形关系，能够较好地处理双向弯曲和轴力耦合的问题.对采用纤维模型建立多向加载作用的恢复力模型研究有：张素梅等[11]利用斜向加载拟静力试验和纤维模型建立了方钢管混凝土压弯构件的弯矩-曲率和荷载-位移恢复力模型.任亮等[12]通过3个施加常轴力的活性粉煤灰混凝土(RPC)箱型桥墩试件的水平反复荷载试验,建立了RPC箱型墩考虑双轴耦合效应的恢复力模型.邓江东等[13]基于双向拟静力试验对粘钢加固箱型墩的双向恢复力模型进行了研究.

本文针对水平双向荷载作用下钢筋混凝土箱型墩恢复力特性研究方面的不足,结合双向拟静力试验开展相关研究,以进一步认识多维地震动作用下钢筋混凝土箱型墩的抗震性能.

1　双向拟静力试验

1.1试验概况

以60 m钢筋混凝土箱型墩为原型,设计为1∶14.3比例的缩尺模型.选取对钢筋混凝土箱型墩滞回特性影响较大剪跨比、轴压比和配箍率等3个主要参数,共设计了11个试件,见表1.按纵筋和箍筋配筋率相等原则，配置模型墩的钢筋.其中，纵筋采用28φ8 mm.对于模型墩B1～B11，墩底区域受力最大，因此在距墩底350 mm墩高范围内，箍筋配置为φ6 mm@50 mm，其他区域箍筋配置为φ6 mm@100 mm；对于模型墩B4，墩底区域的箍筋配置为φ6 mm@70 mm，其他区域为φ6 mm@100 mm；对于模型墩B5，墩底区域的箍筋配置为φ6 mm@100 mm，其他区域箍筋配置为φ6 mm@150 mm.箱型墩截面尺寸为440 mm×320 mm，其中空心部分截面尺寸为260 mm×180 mm，具体见图1.试验中，X方向试件的刚度较大，为强轴方向.相应地，Y方向试件刚度较小，为弱轴方向.采用竖向轴力模拟上部结构质量,有效高度指加载点至墩底距离.实测材料力学性能见表2和表3.试验首先进行预加载，通过在墩顶施加竖向恒载,模拟墩顶质量产生的轴压力.试验中，X与Y方向均采用水平位移等幅逐级加载，每级循环2次.加载过程为：试件屈服前，以2 mm逐级加载；试件屈服后，加载幅值为3 mm；当试件达到极限荷载以后，加载幅值调整为5 mm，直至试件破坏，具体参见文献[7].

表1　桥墩试件设计参数

图1　典型截面钢筋布置图(单位:mm)

表3　钢筋材性参数　MPa

1.2试件破坏模式

本文试验模拟在一定轴力下桥墩在水平双向往复荷载作用下的受力性能和损伤机理.在这种受力状态下,水平荷载较小时,箱型墩构件以受压为主,截面受压;随着水平荷载的增大,箱型墩构件受到较大的压弯作用,截面受到拉压循环荷载作用.其中,墩角位置拉压应力最大.在试验中,观察到11个试件的试验现象基本相似,均呈现出弯曲破坏形态，破坏过程见图2.首先混凝土发生开裂，其中主裂缝出现在2个位置：① 墩底；② 实心段和空心段交界处(见图2(a));钢筋屈服,裂缝沿墩高方向发展(见图2(b))；墩角混凝土剥落(见图2(c))，混凝土压碎,最后形成塑性铰(见图2(d)).所有试件最终破坏形态为墩角混凝土被压碎，并且纵筋发生屈曲和拉断.但裂缝分布范围、剪切裂缝的分布以及塑性破坏的位移和区域均有所不同.其中，试件轴压比越大，则最终的裂缝分布高度越小，剪切裂缝分布也越显著.典型试件B9的破坏形态见图3.试件最终破坏形态图中黑色区域为压碎区域.

(a) 出现横向裂缝　(b) 钢筋屈服

(c) 墩角混凝土剥落　(d) 构件破坏

(a) 最终破坏图片　(b) 最终破坏绘图

2　考虑双向荷载作用的截面弯矩曲率分析

利用OpenSees开放程序进行双向荷载作用的箱型截面弯矩曲率分析.混凝土本构关系采用OpenSees程序自带的混凝土的本构模型Concrete 02，即修正的Kent-Park模型[14].

OpenSees程序包含了2种钢材的本构模型，即Steel 01和Steel 02.其中，Steel 01模型为双线性随动强化模型.强化段的弹性模量取为0.001Es,Es为钢筋初始弹性模量,加卸载时，刚度取初始弹性模量，不考虑钢筋软化.Steel 02和Steel 01均采用Giuffre-Menegotto-Pinto模型，但Steel 02可以考虑等向应变硬化影响，并反映包辛格效应[15].因此,钢筋采用Steel 02材料模型,主要参数包括:钢筋屈服强度fyh、初始弹性模量Es、应变硬化率、双线性模型中弹塑性段分支点附近弧度变化的材料参数R0,CR1，CR2(分别取18,0.925,0.15).

弯矩曲率分析采用牛顿-拉夫森方法，计算结束的应变限值为混凝土的极限压应变.其中,混凝土极限压应变εcu按照下式计算:

(1)

(2)

式中,fyh为箍筋屈服强度.

3　荷载-位移恢复力模型

3.1屈服位移和峰值位移、极限位移

恢复力模型要能够反映结构或构件的非线性特征.一般地,从理论公式推导,能完整、细致地描述结构或构件的非线性特征,但计算公式复杂且计算量很大,难以应用于实际工程.为了使用方便,一般采用折线形恢复力模型.从试验的骨架曲线观察[7],没有明显的开裂荷载点,因此，将恢复力模型的骨架曲线理想地简化为三折线，分别为弹性段、屈服段和荷载下降段.

构件屈服后的骨架曲线均存在着较明显的强化段,对应的特征点为屈服点Y与最大荷载点M.屈服荷载和屈服位移可以通过截面弯矩曲率和构件荷载位移进行理论分析确定,极限荷载和极限位移包含着弯曲、剪切、黏结滑移等引起的塑性变形分析以及二阶效应和塑性铰长度的选择等,理论计算比较复杂.因此，通过统计回归分析极限荷载对应的位移与轴压比、剪跨比和体积配箍率之间的关系，得到的相关参数见表4和表5.

采用通用屈服弯矩法计算得到箱型墩的屈服曲率，极限曲率取核心混凝土边缘达到极限应变对应的曲率.得到屈服曲率后，按弹性阶段曲率线性分布的规则，求得墩顶屈服位移.根据试验数据,水平双向加载的耦合作用使Y方向较早就出现了屈服.因此,在计算屈服位移时,先通过截面分析计算得到X方向的屈服曲率,求得屈服位移,即

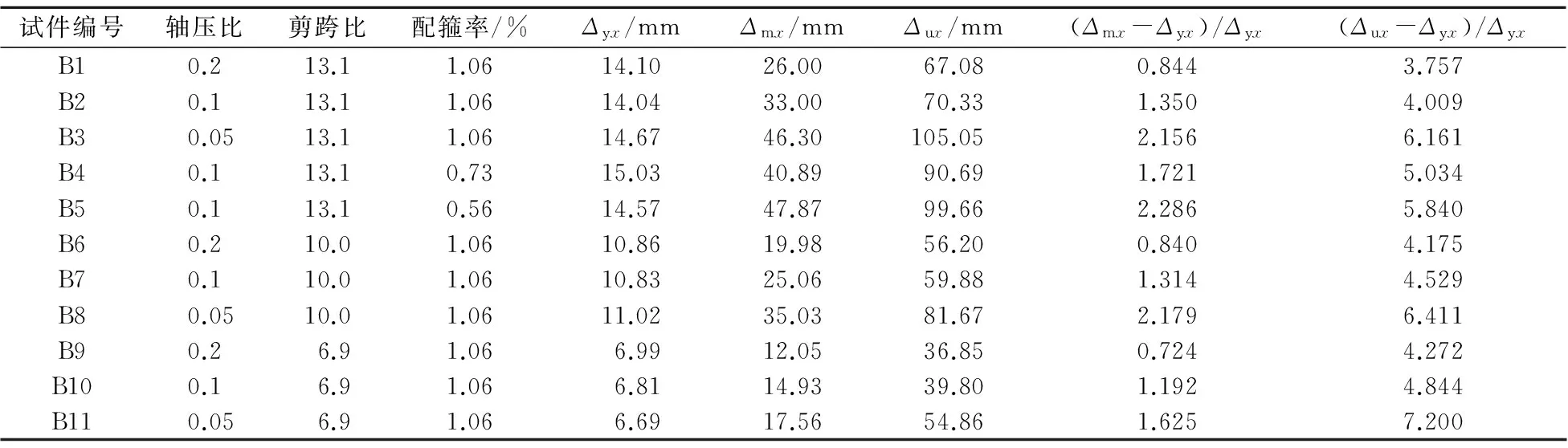
表4　X方向试验参数和特征位移

表5　Y方向试验参数和特征位移

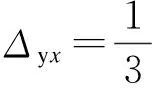
(3)

式中,Δyx为X方向的屈服位移;φyx为X方向的屈服曲率;L为桥墩有效加载高度.然后,令β=Δyy/Δyx,Δyy为Y方向的屈服位移.由回归分析可知,β随轴压比增大而减小,随剪跨比增大而增大,随体积配筋率增大而增大,从而得到β与轴压比n、剪跨比λ和配箍率ρv的回归方程，即

β=0.418-0.035lnn+0.006 2λ+0.284ρv

(4)

回归方程(4)的相关系数R2为0.839 8,检验p值为0.003 6,小于显著性水平0.05,拒绝原假设,即回归模型成立.

根据构件的屈服位移Δy和峰值位移Δm可知,在强化段(Δm-Δy)/Δy随着轴压比增大而减小,随剪跨比增大而增大,随体积配箍率增大而减小.且随剪跨比以及配箍率呈线性变化,随轴压比呈非线性变化.通过相关参数三元线性拟合,可得(Δm-Δy)/Δy与轴压比n、剪跨比λ和箍筋配筋率ρv的关系为

(5)

(6)

式中,Δmx,Δmy分别为X和Y方向最大荷载对应的位移,即峰值位移.

回归方程(5)的相关系数R2为0.939 2,检验p值为0.000 1.回归方程(6)的相关系数R2为0.970 2,检验p值为0.000 1.可以看出,方程具有明显的统计学意义,回归拟合效果较好.

试验构件的屈服位移Δy和极限位移Δu的比值(Δu-Δy)/Δy随着轴压比的增大而减小,随剪跨比的增大而减小,随配箍率的增大而减小.通过相关参数三元线性拟合,可得(Δu-Δy)/Δy与轴压比、剪跨比和箍筋配筋率的关系为

(7)

(8)

式中,Δux,Δuy分别为X和Y方向极限位移,即荷载下降到极限荷载85%时所对应的位移.回归方程(7)的相关系数系数R2为0.861 8,检验p值为0.002 2.回归方程(8)的相关系数系数R2为0.894 8,检验p值为0.000 8.

3.2卸载刚度计算

3.2.1卸载刚度

如果已知卸载点的荷载P、加载位移Δ和荷载为零时的残余变形Δd,则卸载刚度可以表示为

(9)

(10)

式中,Kdx和Kdy分别为墩X和Y方向的卸载刚度;Px,Py分别为墩X和Y方向的荷载；Δdx,Δdy分别为墩X和Y方向的残余变形.

3.2.2残余变形取值

根据双向拟静力试验,试件B1～B11的残余变形见图4.可以看出，箱型墩残余位移基本呈双折线分布，当所施加的外力大于极限荷载值，试件的残余位移明显增大.

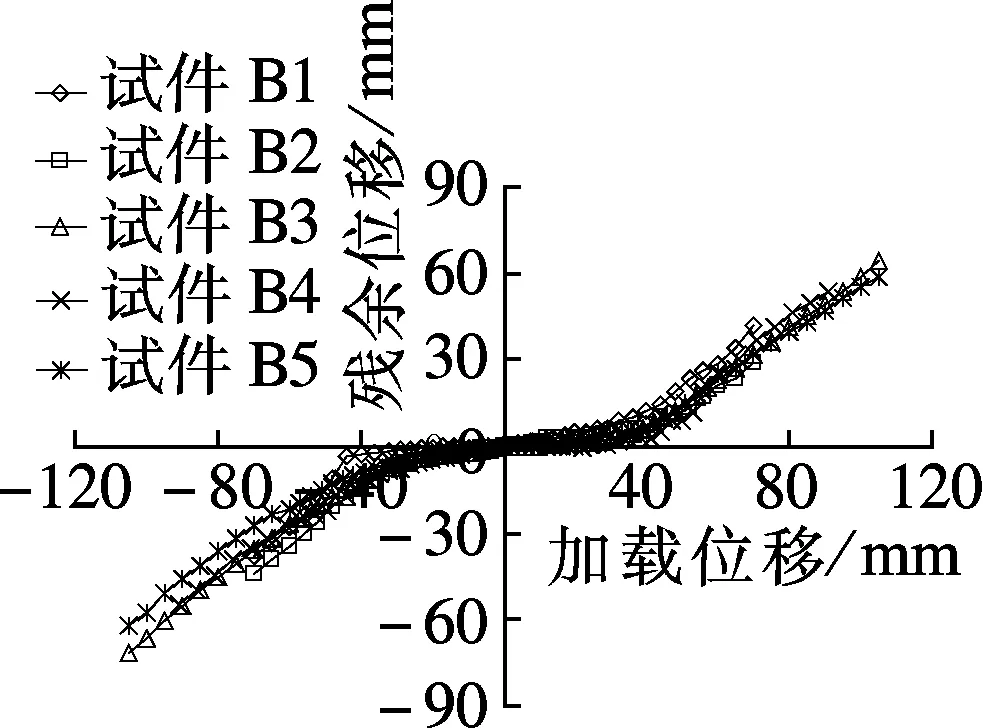
(a) 墩高4.8 m,X方向(b) 墩高4.8 m,Y方向

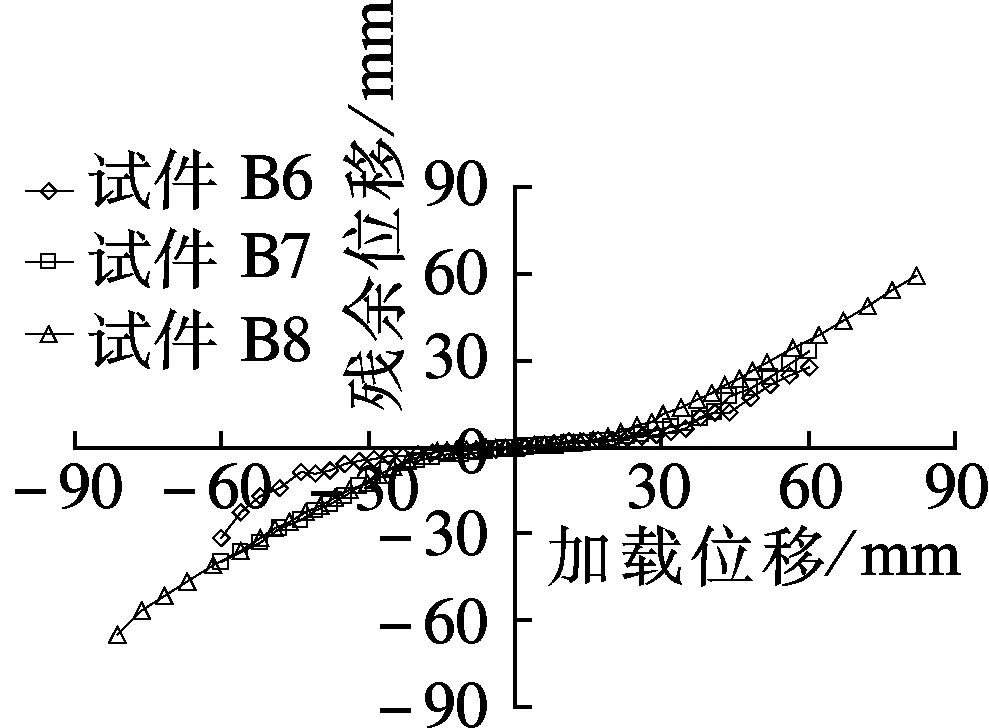
(c) 墩高3.8 m,X方向　　(d) 墩高3.8 m,Y方向

(e) 墩高2.8 m,X方向(f) 墩高2.8 m,Y方向

根据残余变形的特点,建立相对残余变形与轴压比、剪跨比和体积配箍率的关系式.

1) X方向,当加载位移Δ≤Δm时

(11)

当Δ>Δm时

(12)

回归方程(11)的相关系数R2为0.955 6,检验p值为0.001.回归方程(12)的相关系数R2为0.950 0,检验p值为0.000 1.

2) Y方向,当加载位移Δ≤Δm时

(13)

当Δ>Δm时

(14)

回归方程(13)的相关系数R2为0.940 0,检验p值为0.001.回归方程(14)的相关系数系数R2为0.952 1,检验p值为0.000 4.

3.3滞回规则的拟定

根据双向拟静力试验,钢筋混凝土箱型墩仍然以弯曲破坏为主.因此,以Takeda模型[16]为基础,根据实验荷载-位移滞回曲线特点,采用四线折线形滞回模型,包括弹性线段、强化阶段、强度退化段以及卸载段.该模型可以很好地反映结构进入强震后的非线性特性,以及由于混凝土开裂、钢筋屈服和混凝土压碎等引起的结构刚度退化、强度退化和残余变形增大等特点,反映了结构的力学行为机理.因此,确定基本滞回规则为:① 构件屈服前，加卸载都按骨架曲线进行.② 构件屈服强度后,加载按照骨架曲线进行,卸载随卸载刚度Kd线性变化.③ 反向以及再加载路径.构件反向受力屈服后，进行反方向加载，反向加载沿着卸载线与位移轴的交点和骨架曲线正方向达到最大位移所对应点之间的连线进行.④当某一个方向后续循环的位移幅值没有超过该方向已经达到的最大位移幅值时，反向加载及再加载路径和该方向前一个循环加载路径相同.

根据加卸载准则,确定的特征点和加卸载规则描述见图5.图中,Ke,Ku和Kd分别表示弹性阶段刚度、退化刚度和卸载刚度,M,M′分别为极限荷载点,U,U′分别为极限位移点.点1表示屈服点,点2表示强化段上的卸载点,点3为屈服后卸载与位移轴的交点,点4为反向加载屈服点,点5为反向加载的最大位移点,点6为反向屈服后卸载与位移轴的交点,点7为极限荷载点,点7和点8连线的斜率为下降段刚度,点8和点9连线的斜率为从第8点卸载的刚度,点10为再次反向加载的最大位移,点11和点12连线的斜率为反向经过最大荷载后从点11卸载的刚度.

图5　滞回模型

3.4理论恢复力模型

建立理论恢复力模型基本步骤如下:

① 计算屈服位移Δy和屈服荷载Py.箱型墩墩顶的屈服位移按式(3)和式(4)计算.由于屈服时水平位移较小,因此不考虑轴力引起的附加弯矩.根据力平衡条件,可求得箱型墩屈服时的墩顶水平荷载为

(15)

(16)

式中，Pyx,Pyy为X,Y方向的屈服荷载；Myx,Myy为X,Y方向的屈服弯矩.

② 计算最大荷载Pm及其对应的位移Δm.根据式(5)和(6)可分别求得X方向和Y方向的位移Δmx和Δmy.然后通过下式求得X方向和Y方向的最大荷载Pmx,Pmy,即

(17)

(18)

式中,Hu为加载点至塑性铰一半的高度,Hu=L-LP/2,LP的求解公式[17]为

LP=0.5h+0.05L-15ρvh

(19)

式中,h为荷载作用方向截面高度.

③ 计算极限荷载Pu和极限位移Δu.极限荷载Pu按0.85Pm计算,墩顶位移Δu按式(7)和式(8)计算.

④ 确定滞回曲线.根据式(9)～(14)可以得到骨架曲线上各点对应的卸载刚度,从而根据已经确定的滞回规则求得双向荷载作用下钢筋混凝土箱型墩的荷载-位移滞回曲线.

4　实测和计算恢复力模型比较

4.1荷载-位移骨架曲线

根据理论方法，计算得到钢筋混凝土箱型墩理论荷载-位移骨架曲线，并与实测曲线进行比较，见图6.图中，试验曲线特征值为该曲线正负特征点绝对值的平均值.可以看出,采用计算恢复力模型骨架曲线总体上能够反映出实测骨架曲线的趋势,数值比较接近.说明理论骨架曲线的屈服、峰值荷载和极限位移等特征点与实测值较为接近,可以反映构件整体刚度和强度的变化.

(a) 试件B1,X方向　(b) 试件B1,Y方向

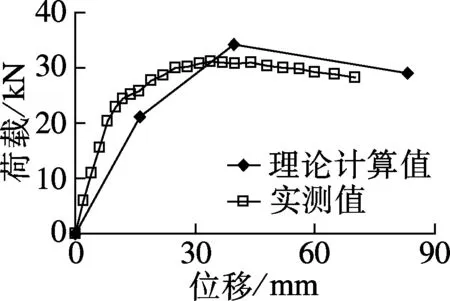
(c) 试件B2,X方向　(d) 试件B2,Y方向

(e) 试件B3,X方向　(f) 试件B3,Y方向

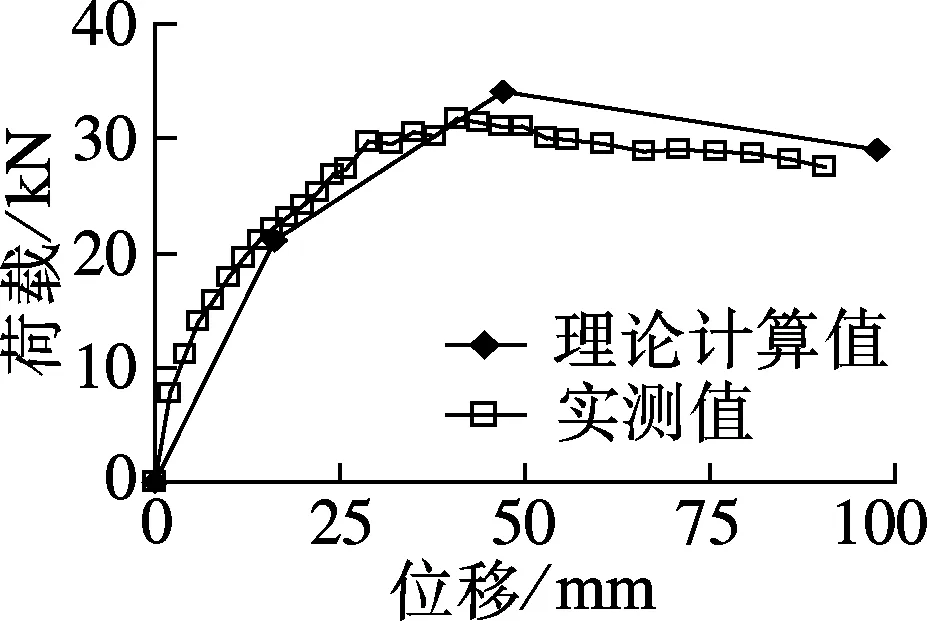
(g) 试件B4,X方向　(h) 试件B4,Y方向

(i) 试件B5,X方向　(j) 试件B5,Y方向

4.2荷载-位移滞回曲线

根据滞回规则,计算得到荷载-位移滞回曲线,并与实测滞回曲线比较(见图7).可以看出,理论计算的滞回曲线总体上能够反映出实测滞回曲线的趋势,刚度退化也较为接近,理论计算值与试验值基本吻合.说明理论恢复力模型可以反映出钢筋混凝土箱型墩的基本抗震性能以及滞回耗能等特点.

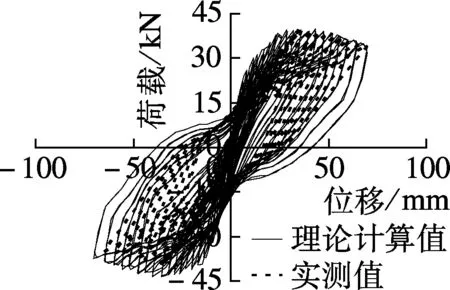
(a) 试件B1,X方向　(b) 试件B1,Y方向

(c) 试件B2,X方向　(d) 试件B2,Y方向

(e) 试件B3,X方向　(f) 试件B3,Y方向

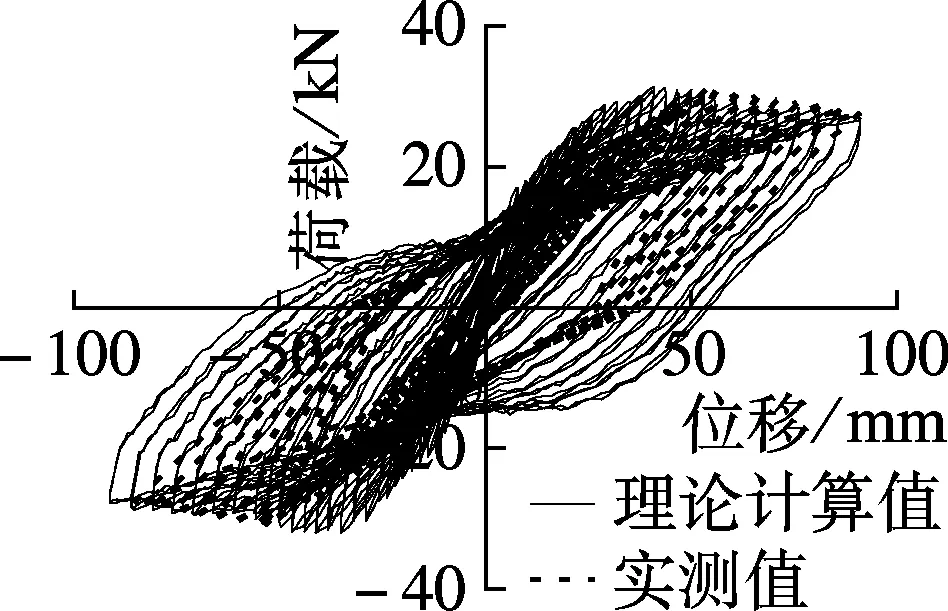
(g) 试件B4,X方向　(h) 试件B4,Y方向

(i) 试件B5,X方向　(j) 试件B5,Y方向

(k) 试件B6,X方向　(l) 试件B6,Y方向

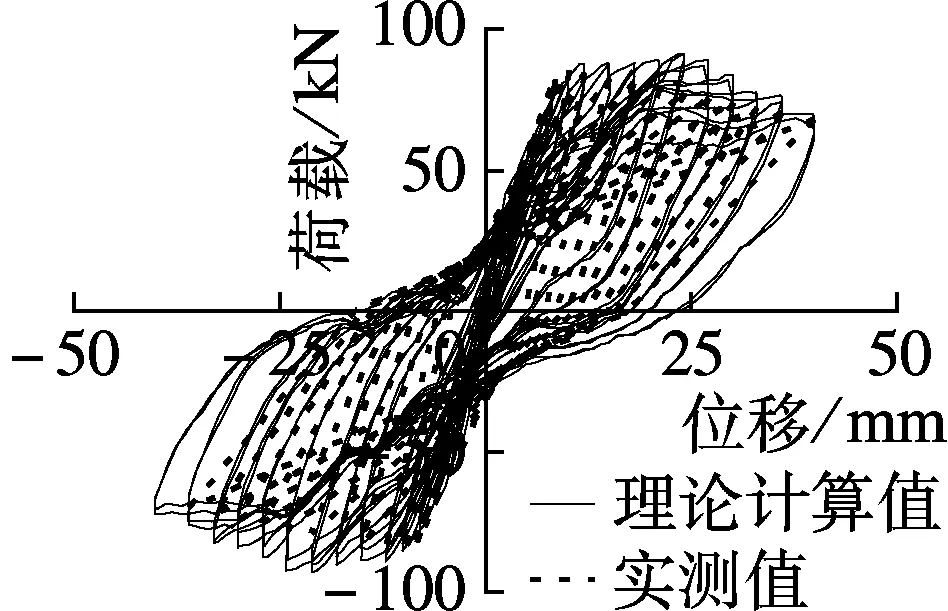
(m) 试件B7,X方向　(n) 试件B7,Y方向

5　结论

1) 在双向拟静力试验研究的基础上,进行了双向荷载作用下钢筋混凝土箱型截面的弯矩-曲率分析,并得到考虑双向荷载耦合作用的屈服位移计算影响系数,建立了钢筋混凝土箱型墩屈服位移的计算公式.

2) 根据实测骨架曲线的特点,得到了峰值位移、极限位移与剪跨比、轴压比和体积配箍率之间的计算公式,并建立了反映双向荷载影响的残余变形和卸载刚度的计算方法.根据弯曲破坏为主的破坏模式,以及适合于试验特点的荷载-位移滞回规则,建立了钢筋混凝土箱型墩荷载-位移双向恢复力模型.

3) 实测和理论计算骨架曲线、滞回曲线都吻合良好,因此，可认为结合拟静力试验、数值统计分析和理论分析建立的恢复力模型很好地体现了钢筋混凝土箱型墩的荷载-位移特征值和滞回耗能的特点,较好地反映钢筋混凝土箱型墩的抗震性能,可以应用于钢筋混凝土箱型墩结构的弹塑性抗震性能分析.

References)

[1]Yeh Y K, Mo Y L, Yang C Y. Seismic performance of rectangular hollow bridge columns [J].JournalofStructuralEngineering, 2002, 128(1): 60-68. DOI:10.1061/(ASCE)0733-9445(2002)128:1(60).

[2]Pinto A V, Molina J, Tsionis G. Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section[J].EarthquakeEngineeringandStructuralDynamics, 2003, 32(13): 1995-2012.

[3]罗征, 李建中. 低周往复荷载下空心矩形墩抗震性能试验研究[J]. 振动与冲击, 2013, 32(8): 183-188.

Luo Zheng, Li Jianzhong. Tests for a seismic performance of rectangular hollow thin-walled bridge columns under low-cycle reversed loading [J].JournalofVibrationandShock, 2013, 32(8): 183-188.(in Chinese)

[4]杜修力, 陈明琦, 韩强. 钢筋混凝土空心桥墩抗震性能试验研究[J]. 振动与冲击, 2011, 30(11):254-259.

Du Xiuli, Chen Mingqi, Han Qiang. Experimental evaluation of seismic performance of reinforced concrete hollow bridge columns [J].JournalofVibrationandShock, 2011, 30(11):254-259. (in Chinese)

[5]孙治国. 钢筋混凝土桥墩抗震变形能力分析[D]. 北京: 中国地震局工程力学研究所, 2012.

[6]Han Q, Du X L, Zhou Y H, et al. Experimental study of hollow rectangular bridge column performance under vertical and cyclically bilateral loads[J].EarthquakeEngineeringandEngineeringVibration, 2013, 12(3): 433-445. DOI:10.1007/s11803-013-0184-y.

[7]夏樟华, 宗周红, 钟儒勉. 基于双向拟静力试验的钢筋混凝土箱型薄壁墩抗震性能[J]. 东南大学学报(自然科学版), 2013, 43(1): 180-187. DOI:10.3969/j.issn.1001-0505.2013.01.034.

Xia Zhanghua, Zong Zhouhong, Zhong Rumian. Seismic performance of reinforced concrete thin-walled piers with rectangular hollow cross-sections based on bi-axial quasi-static testing [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2013, 43(1): 180-187.DOI:10.3969/j.issn.1001-0505.2013.01.034. (in Chinese)

[8]Nishimura K, Takiguchi K, Nguyen H H. Tri-axial non-linear restoring force model of R/C structures by using an analogy to the plastic theory [C]//13thWorldConferenceonEarthquakeEngineering. Vancouver, Canada, 2004: 450-1-450-14.

[9]杜宏彪. 双向压弯钢筋混凝土柱的抗震性能[J]. 哈尔滨建筑大学学报,1999, 32(4):47-52.

Du Hongbiao. The seismic behavior of bi-directional compression-flexure reinforced concrete columns[J].JournalofHarbinUniversityofCivilEngineeringandArchitecture, 1999, 32(4):47-52.(in Chinese)

[10]刘林. 高墩大跨铁路桥梁抗震设计与减震控制研究[D]. 北京:北京交通大学土木建筑工程学院, 2004.

[11]张素梅, 刘界鹏, 王玉银, 等. 双向压弯方钢管高强混凝土构件滞回性能试验与分析[J]. 建筑结构学报, 2005, 26(3):9-18.

Zhang Sumei, Liu Jiepeng, Wang Yuyin, et al. Hysteretic behavior of bi-axially loaded high strength concrete-filled square hollow section beam-columns[J].JournalofBuildingStructures, 2005, 26(3):9-18.(in Chinese)

[12]任亮, 方志, 王诚. 考虑双轴水平力耦合效应的RPC箱型桥墩恢复力模型试验研究[J]. 地震工程与工程振动,2012, 32(2):152-159.

Ren Liang, Fang Zhi, Wang Cheng. Experimental study on the restoring force model of reactive powder concrete box piers under biaxial horizontal loads [J].JournalofEarthquakeEngineeringandEngineeringVibration, 2012, 32(2):152-159. (in Chinese)

[13]邓江东,宗周红,刘爱荣. 粘钢加固钢筋混凝土箱型桥墩双向恢复力模型研究[J]. 工程力学, 2013, 30 (12): 115-122,131.

Deng Jiangdong, Zong Zhouhong, Liu Airong. Study on bi-directional model of restoring force of hollow reinforced concrete piers strengthened by adhering steel Plates [J].EngineeringMechanics, 2013, 30(12): 115-122,131. (in Chinese)

[14] Mazzoni S, McKenna F, Scott M H, et al.OpenSeesusersmanual[M]. Berkeley, UAS: University of California, 2004:137-160.

[15]张继承,林振宇.低周反复荷载下异形钢管混凝土柱力学性能有限元分析[J]. 武汉工程大学学报, 2010, 32(5): 60-65. DOI:10.3969/j.issn.1674-2869.2010.05.017.

Zhang Jichen, Lin Zhenyu. Finite element analysis on mechanical properties of special-shaped concrete-filled steel tubular under low cyclic loading[J].JournalofWuhanInstituteandTechnologyUniversity, 2010, 32(5):60-65. DOI:10.3969/j.issn.1674-2869.2010.05.017. (in Chinese)

[16]Takeda T, Sozen M A,Nielson N N. Reinforced concrete response to simulated earthquakes[J].JournalofStructuralDivision, 1970, 96:2557-2572.

[17]夏樟华,宗周红. 钢筋混凝土箱型墩延性抗震性能研究[J]. 振动与冲击, 2013, 32(23):151-158. DOI:10.3969/j.issn.1000-3835.2013.23.027.

Xia Zhanghua, Zong Zhouhong. Ductility a seismic performance of reinforced concrete box piers[J].JournalofVibrationandShock, 2013, 32(23):151-158. DOI:10.3969/j.issn.1000-3835.2013.23.027.(in Chinese)

Biaxial restoring force characteristics of reinforced concrete box piers

Xia Zhanghua1Zong Zhouhong2

(1School of Civil Engineering, Fuzhou University, Fuzhou 350108, China) (2School of Civil Engineering, Southeast University, Nanjing 210096, China)

To establish the simplified analysis model for elastoplastic seismic response of reinforced concrete box piers subjected to bidirectional seismic excitation, the load-displacement restoring force characteristics subjected to the bidirectional cyclic load were analyzed. First, the basic situation and the failure mode of the biaxial quasi-static test were introduced. Secondly, the calculation methods for the peak displacement, the ultimate displacement, and the residual deformation of the box pier were established combined moment curvature relationship analysis of the box section under the biaxial compression and bending load. The calculating formulas of the three-segment-line load-displacement skeleton curve and the unloading stiffness were further presented, and the corresponding theoretical bidirectional restoring force models were developed. Finally, the theoretical bidirectional restoring force models were analyzed and verified by testing results. The results show that the bending failure is the main failure mode of the reinforced concrete box pier under the bidirectional cyclic load. The theoretical load displacement skeleton curve and the hysteresis curve agree well with the test ones, and the theoretical restoring force model considering the bidirectional cyclic load can reveal the basic anti-seismic performance of reinforce concrete box piers.

reinforced concrete box piers; biaxial quasi-static test; residual deformation; skeleton curve; hysteresis curve

10.3969/j.issn.1001-0505.2016.04.025

2015-11-04.作者简介: 夏樟华(1980—)，男，博士，副研究员；宗周红(联系人)，男，博士，教授，博士生导师，zongzh@seu.edu.cn．

国家自然科学基金资助项目(51408360)、国家教育部博士点基金资助项目(20110092110011).

10.3969/j.issn.1001-0505.2016.04.025.

U443.22

A

1001-0505(2016)04-0823-08

引用本文: 夏樟华，宗周红.钢筋混凝土箱型墩的双向恢复力特性[J].东南大学学报(自然科学版),2016,46(4):823-830.