应急救援中人员及物资综合调度优化

李玉兰，陈锦耀，柴树峰

(军事交通学院 军事物流系，天津 300161 )



应急救援中人员及物资综合调度优化

李玉兰，陈锦耀，柴树峰

(军事交通学院 军事物流系，天津 300161 )

为提高我国军民融合应急救援能力，以中西部经济欠发达地区的突发事件为研究对象，建立基于多出救点且要求为应急开始时间最早和可靠的救援人员一次性应急调度模型，以及连续性消耗的应急物资调度数学模型。综合考虑在路网复杂性、天气等多种因素影响下的人员物资综合调度模型，从有限应急时间下连续性应急物资调度和有限应急时间下一次性救援人员调度两方面建立综合数学模型来分析实际的应急救援调度管理。并由仿真算例验证了模型的可行性。

应急救援；物资；人员；综合调度

在我国军民融合应急物流管理模式下[1-3]，部队和地方通常共同完成应急工作，部队官兵主要作为救援人员参与，地方民政部门组织完成物资供应。在实际的应急救援工作中，往往是专业救援人员和救援物资分路并进，需要多出救点配合行动。但这种情况可能会因救援人员先到而物资不到造成抢救时间浪费，也可能会因物资先到而专业救援管理人员不到，造成物资损失等问题。在多出救点应急物资调度问题上，刘春林等[4]研究了应急系统中多点出救问题，提出了基于连续可行性约束建立以最早应急开始时间为目标的数学模型；何建敏[5]根据应急事件的时间紧急性要求，给出了限制期下的多出救点组合模型，分析了多出救点的优化解决方案；汪欲等[6]建立了在多资源多出救点的应急系统中基于出救点个数最少和应急开始时间最早的多目标的调度模型；戴更新[7]以单资源的研究成果为基础，在多资源连续可行情况下，给出了应急时间最早的前提下出救点数目最少的数学模型。还有一些国内外学者对大规模物资运输、满意度、需求预测等方面进行了研究[8-12]。上述应急物资调度问题大多数是以纯数学方法、在理想条件下进行推理和分析，约束条件过于简单，或者只是以较小的局部地区进行分析和论证，对于大规模应急物流工作的应用有一定限制。本文以地广人稀的中西部等经济发展欠发达地区的应急事件发生情况为主要研究对象，研究基于多出救点的人员及物资综合应急调度问题。

1　应急救援中人员及物资综合调度模型的建立

由于我国经济发展不平衡，在乡村、山区、边疆以及西部省份等地区，交通、信息、物资保障等方面较难达到有效保障，需要从物资调度和救援人员调度两方面来综合分析调度的有效性。当发生应急事件时，通常有两种调度方式：一是救援人员的调度，通常类似为限制期一次性消耗问题；二是连续性物资调度，根据应急事件的性质，通常为限制期内连续性消耗问题，即首先要在最短时间内保证提供一定数量的物资，之后是持续供应，不能间断。根据这些要求，从效率及成本两方面考虑，必须满足连续消耗条件下“应急时间最早”及“可靠性”的物资调度要求，这一要求可以通过对供应方法及供应方式两方面进行综合研究来实现。

1.1救援人员的一次性调度

基于我国的现状，在较为短暂的应急事件和非长期军事战争情况下，大量的军队、武警人员的运输通常为一次性到达。由于人员集中，不需要多地人员集合后统一投送，其主要的调度要求为应急开始时间最早和可靠。根据这一特点，可设模型如下。

φ={(A1，x1)，(A2，x2)，…，(Ap-1，xp-1)，(Ap，

1.2基于连续性消耗的应急物资调度

应急活动开始后，必须要满足最低救援物资数量要求才能开始救援。最低救援量的物资中第一批物资到达的最早时间为t0，应急物资的消耗速率为v，从Bj到B需要的时间为tj(tj>0)，要求给出一方案在保证连续性条件下，即应急物资连续供应的条件下，应急开始时间最早，主要是需要确定参与应急的出救点及各自提供的应急资源数量。

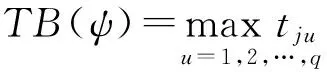
1.3多因素综合的最短时间分析

从实际考虑，应急事件发生时的各种不确定因素很多，包括天气、道路、安全因素等，因而通常是救援人员和最低救援需求数量的应急物资均到达时才开始进行应急救援，整个应急救援工作的展开就必须考虑人和物的全部到位。从实际情况分析，真正要求的应急最早时间为两者到位的最迟时间。这样应急开始时间最早的模型为max{minTA(φ)，minTB(ψ)}。

此外，由于道路上不确定的时间较多，必须考虑留出运输时间余量，才能客观分析应急最短时间的准确性，为应急工作的良好处理做好坚实基础。影响时间不确定的因素较多，其中最重要的是路网的不确定性。交通路网的不确定因素通常是由自然灾害、交通事故、反恐安全等造成的，特别是地震、洪水等重大事件会导致路段完全封闭，严重削弱路网性能。为简便起见，可对某些连通路段通过交通时间影响因子λ来衡量，从而原有的时间变为

式中λ为实际道路交通影响因子，值越大则越难行进，当道路阻断以及超过原有时间5倍以上时认为是无限大，λ∈[-1，1]。

这样，就得到了包括考虑实际道路交通影响因子的人和物共同到达应急地点的最短应急时间模型为

max{minTA(φ)(1+λ)，minTB(ψ)(1+λ)}

(1)minTA(φ)(1+λ)为人员到达最短应急开始时间。

因为t1≤t2≤…≤tp，因此在tp之前能够到达的全部人数肯定小于x，故最早应急时间一定不小于tp，这样就得到出救人员到达的最早应急时间的计算为

TA(φ)(1+λ) =maxti(1+λi)i=1,2，…,p

应急最早时间取其最大值即可。

(2)minTB(ψ)(1+λ)为物资到达最短应急时间。

(1)

式(1)左边表示t时刻已经到达(含已消耗)的物资量，右边表示从开始应急到时刻t的应急物资消耗量。如果t1﹤t2﹤…﹤tq，则对应的最早开始时间为

(2)

2　仿真算例

2.1算例数据

假设我国西部某地连降大雨，河流沿线多处受灾，急需救援物资y=600 t及救援人员x=200单位，应急物资的消耗速率v=14单位/h，需要从9个应急物资储备中心及7个军队驻地调度，其基本数据见表1和表2。救援人员要求一次性到达，应急物资需要达到最低需求量，之后才能开始救援工作。应急物资储备中心和军队驻地以及应急地区的地理位置已知，可得到其相对坐标位置。判断其开始应急救援的最早时间。

表1　物资调度数据(y=600 t，v=14单位/h)

表2　救援人员调度数据(x=200单位)

2.2求解

根据之前所述，对于物资调度及人员调度分别进行计算。首先对连续运输的物资调度时间进行分析计算，之后对人员调度时间进行计算。

(1)物资调度最早应急时间。

由表1可知，对物资调度时间进行实际影响因子加权计算后，可知为(t6，6)<(t1，6.3)<(t2，7.2)<(t3，7.5)<(t4，9.31)<(t5，9.6)<(t9，12.6)<(t8，14.2)<(t7，23.8)。取最短时间出救点，则参与救援的应急物流中心组合：B6(6，120)、B1(6.3，70)、B2(7.2，50)、B3(7.5，80)、B4(9.31，130)、B5(9.6，130)和B9(12.6，20)。

由于物资调度为连续性行为，其速率为v=14单位/h，根据式(2)计算可得

tstart=max(6，6.3-120/14，7.2-(120+70)/14，7.5-(120+70+50)/14，9.31-(120+70+50+80)/14，9.6-(120+70+50+80+130)/14，12.6-(120+70+50+80+130+20)/14)=

max(6，-2.27，-6.37，-9.64，-13.54，

-22.54，-30.25)=6 h

最早的最低需求物资完成时间为

tend=6+600/14=6+42.9=48.9 h

为了保险起见，通常还要考虑物资的损耗情况，因而一般实际物资起运数量为600×(1+10%)=660单位，从而最终时间约为54 h。

(2)人员调度最早应急时间。

由表2可知，对人员调度实际影响因子加权后，其值为(t1，1.4)﹤(t5，6) ﹤(t2，7.2)﹤(t4，10.2)﹤(t3，10.5)﹤(t6，13.3)﹤(t7，39.1)。由于其为一次性调度情况，只要遵循时间最短、出救点数目最少就可以了。因此参与救援的军队驻地组合为A1(1.4，55)、A5(6，54)、A2(7.2，71)和A4(10.2，20)，人员调度最早应急开始时间为tend=10.2 h。

根据上述计算取两者之间的最大值，最早应急开始时间为54 h。在这种情况下，救援人员先于应急物资到达应急地点，可以在相对很短的时间内开展救援工作。

3　结　语

当前我军和地方条块分割的应急物流管理模式在面临大规模应急事件时容易出现诸多问题，本文在总结多出救点应急物资调度问题研究成果的基础上，以地广人稀的中西部经济发展欠发达地区的应急事件发生地为主要研究对象，建立包括应急最短时间和可靠性约束的多出救点应急救援人员的一次调度模型，以及保证物资足够供应约束的应急物资连续消耗性调度模型，最后综合以上条件建立了人员及物资综合调度的数学模型，并以此模型给出算例，得到较好的解。期望这些模型的建立能对我国军民融合应急管理模式下的应急调度问题提供一些解决方法和手段。

[1]王宗喜,张志鹏,张磊. 略论军事物流与应急物流协同发展战略[J]. 后勤学术, 2010 (11): 64-66.

[2]沈昌礼,祝刚,乔伟. 军地一体应急物流体系建设的思考[J]. 军事交通学院学报, 2010, 12 (4): 68-70.

[3]张德,龚延成. 加强军地一体应急物流体系建设[J]. 国防大学学报, 2011(2): 81-83.

[4]刘春林,何建敏,盛昭瀚. 多出救点应急系统最优方案的选取[J]. 管理工程学报, 2000, 14(1): 13-16.

[5]何建敏,刘春林. 限制期条件下应急车辆调度问题的模糊优化方法[J]. 控制与决策, 2001, 16(3): 318-321.

[6]汪欲,何建敏. 应急系统中多资源出救方案的研究[J]. 东南大学学报(自然科学版), 2002, 32(3): 510-513.

[7]戴更新,达庆利. 多资源组合应急调度问题的研究[J]. 系统工程理论与实践, 2000，20(9): 52-55.

[8]陈雷雷,王海燕. 大规模突发事件中基于满意度的应急物资优化调度模型[J]. 中国安全科学学报, 2010, 20(5): 46-52.

[9]缪成,许维胜,吴启迪. 大规模应急救援物资运输模型的构建与求解[J]. 系统工程, 2006, 24(11): 6-12.

[10]SONG H.Tourism demand modeling and forecasting — A review of recent research[J].Tourism Management, 2008, 29(2): 203-220.

[11]高淑萍,刘三阳. 基于联系数的多资源应急系统调度问题[J]. 系统工程理论与实践, 2003,23(6): 113-116.

[12]王玲玲. 多出救点应急调度研究[J]. 铁道运输与经济, 2010, 32(7): 47-52.

(编辑：史海英)

Optimization of Supply-Personnel-Integrated Scheduling in Emergency Rescue

LI Yulan, CHEN JinYao，CHAI Shufeng

(Military Logistics Department, Military Transportation University, Tianjin 300161,China)

To improve the civil-military-integrated emergency rescue capability of our army, this paper studies the emergency incidents in the less developed central and western regions. It establishes a one-time emergency rescue personnel scheduling model which involves multiple rescue points and requires earliest and reliable rescue. A continuously-consuming emergency supply scheduling model is also established. A supply-personnel-integrated scheduling model on the base of complicated road network and weather conditions is then established. The simulation example verifies the feasibility of the model.

emergency rescue; supply; personnel; integrated scheduling

2016-01-15；

2016-03-15.

军事交通学院科研基金项目(2016B55).

李玉兰(1974—)，女，博士，讲师.

10.16807/j.cnki.12-1372/e.2016.08.013

E233

A

1674-2192(2016)08- 0056- 04