运用Excel工具优化战略投送基地选址

海　军，刘顺尧，杨　军

(1.军事交通学院 联合投送系，天津 300161； 2.军事交通学院 研究生管理大队，天津 300161)



运用Excel工具优化战略投送基地选址

海军1，刘顺尧2，杨军2

(1.军事交通学院 联合投送系，天津 300161； 2.军事交通学院 研究生管理大队，天津 300161)

为解决战略投送基地优化选址问题，基于整数规划和离散点选址问题，建立了战略投送基地集合覆盖数学模型，运用Excel工具对战略投送基地进行优化选址，为战略投送基地的实际选址提供一种简便可行、易操作的量化方法。

战略投送基地；选址；Excel工具

战略投送基地是我军战略投送体系的核心支撑，是现代军事物流体系的重要环节，是应急救援体系的有机补充，在我军新型作战力量体系中具有十分重要的地位。战略投送基地优化选址是军事运输系统规划的重要内容，其主要研究的是在国土疆域(战区)范围内，根据作战力量、保障力量的部署位置，合理选择一个或多个地址规划建设战略投送基地的优化决策过程，目的是以较少的资源投入实现就近就便精确化投送保障。目前，国内外针对选址问题主要采用重心法、最优化规划方法、启发式算法和网络分析方法等，对于规模较大的军事运输系统规划决策问题，需要进行大量的数学计算。而Excel作为一种较普及的应用软件，提供了很多常用的数学函数，有很强的处理军事运筹学问题的功能，且较之Matlab和Lingo专业数学软件易于理解、操作方便[1]，为此，本文运用Excel工具解决战略投送基地的优化选址问题。

1　战略投送基地选址模型与算法

1.1选址模型

选址问题模型通常可分为连续点选址和离散点选址模型，对于连续点选址一般采用交叉中值和精确重心算法。本文研究的是离散点选址问题。所谓离散点选址，指的是在有限的候选位置中，选取最为合适的一个或一组位置为最优方案，相应的模型称作离散点选址模型。其与连续选址模型的区别在于，它所拥有的候选方案只有有限个元素，只需要在这几个有限的位置进行分析。

对于离散点选址问题，主要有覆盖模型(covering)和P-中值模型。所谓覆盖模型，指的是对于已知的一些部队投送需求点，确定一个或多个战略投送基地满足部队的投送需求，需要确定基地的最小数量和合适的位置。依据解决问题方法的不同可分为两种不同的模型：一是集合覆盖模型(set covering location problem)，即用最少的战略投送基地数量去覆盖所有的部队投送保障需求点；二是最大覆盖模型(maximum covering location)，即用给定数量的战略投送基地覆盖尽可能多的部队投送保障需求点。

按照上述定义，本文目标是用尽可能少的战略投送基地数量覆盖所有部队投送保障需求点，所以选择集合覆盖模型，其数学模型为

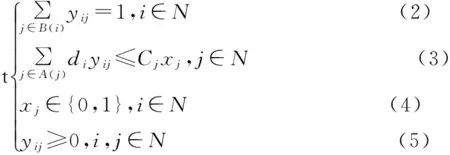
式中：N为部队投送保障需求点集合，N={1，2，…,n}；di为第i个需求点的需求量；Cj为战略投送基地j的保障能力；A(j)为战略投送基地j覆盖所有部队投送保障需求点的集合；B(i)为可以覆盖部队投送保障需求点i的战略投送基地j的集合，B(i)={j|i∈A(j)}；xj为投送基地是否位于投送节点j的标度，xj= 1表示该投送基地位于节点j，xj= 0表示该投送基地不位于节点j；yij为i需求点的需求量被分配给战略投送基地j的比例。

上述各式涵义：式(2)为每个部队投送保障需求点的需求得到完全满足；式(3)为每个战略投送基地保障能力的限制；式(4)为一个候选地点最多只能规划建设一个战略投送基地；式(5)为允许一个战略投送基地为某个部队投送保障需求点提供部分需求。

1.2选址算法

目前，有关选址问题的算法主要有：

(1)解析法。通常运用运筹学的分枝定界方法，能够找到小规模问题的最优解[2]。因其数学模型简单，考虑因素较少，主要适用于单个基地选址问题。

(2)最优化规划方法。要求在一些特定的约束条件下，从许多可用的选择中挑选出一个最佳方案。特点是能够获得较为精确的最优解，但对一些复杂问题构建恰当的数学模型较为困难，或者模型太复杂，具有NP-Hard 性质，存在着变量与约束条件数量上的维数灾难。

(3)启发式方法。这种算法是一种逐次逼近最优解的方法，所得到的结果不一定能够保证是最优解，但可以保证是可行解，适用于大规模系统优化选址问题的分析求解。

(4)图论与网络分析方法。在基地选址问题中，点表示可供选择的基地，其间的连线(边)则表示距离、流量或运输费用。这种由顶点、边和某些数量指标组成的图，能形象清晰地描述空间中的位置关系，可定量处理许多问题，所以利用图论知识也可有效解决选址问题。

上述分析的数学模型是典型集合覆盖问题的一种推广，但存在NP-Hard问题。为使其具有推广应用价值，可运用Excel工具软件简便高效地加以求算，非常适于战略投送基地的优化选址问题。

2　战略投送基地优化选址算例

根据上级要求，拟在某战区范围内的v={v1，v2，…，vn}10处备选地规划建设战略投送基地，{v1，v2，…，vn}代表部队驻地或部队预定集结地域，要求战略投送基地保障部队需求的距离不大于500 km，图1中各线段标示的数字代表两点之间的距离。经考察，v1点和v10点由于交通不便，不适宜作为战略投送基地选址，因此，除了v1点和v10点外，其他地点均可作为战略投送基地的候选地点。

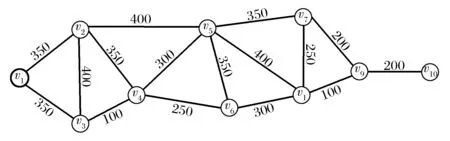
图1　战略投送基地优化选址算例示意

2.1求算两两节点间距离

按照流量平衡计算方法：净流量 = 流出某节点的流量 -流入某节点的流量，中间各节点流量应保持平衡。为此，起点v1设为1，终点v10设为-1，各个节点的净流量等于平衡值。

根据图1，按照图论最短路径算法，依次求取两两点间的距离d(如图2所示)。在Excel中单元格B4:B19，C4：C19中分别输入图1的起点和终点；单元格E4：E19输入两两节点间的距离；在单元格G4：G13输入图1的终点；在单元格H4：H13中计算净流量，如H4=SUM(D4:D5)、H5=SUM(D6:D8)-D4，等等。在单元格D21计算最短路线：D21=SUMPRODUCT(D4:D19,E4:E19)。

在规划求解时设定目标$D$21为最小值，可变单元格$D$4:$D$19，在约束中添加$H$4=1, $H$5:$H$12=0, $H$13=-1，求解方法为单纯线性规划，之后求解，计算结果如图2所示。

图2　最短路线求算过程

按照上述方法，依次求出两两节点间最短路(如图3所示)。

2.2预处理

在单元格B2：K11中输入两两节点间距离，在单元格M3中输入距离约束500。根据距离约束，求解各节点是否可以作为战略投送基地的候选点。通过判断单元格B2:K11数据与单元格M3中数据的大小，用“1”表示使用该点，用“0”表示该点不满足距离要求。如在单元格B15中输入公式:=IF(B2<=$M$3,1,0)。数据预处理结果如图4所示。

图4　数据预处理

得到的数据见单元格B15:K24。注意，因节点v1和v10不能作为战略投送基地的候选点，故单元格B15:B24，K15:K24全为0(如图5所示)。

图5　战略投送基地优化选址求算过程

2.3建立0-1整数规划模型

在Excel中描述整数规划问题的决策变量、目标函数和约束条件。

本问题的决策变量为:是否选用该点作为战略投送基地选址点，用“1”表示使用该点，用“0”表示不使用该点。在Excel工作表上用单元格B26:K26表示决策变量，分别表示10个节点是否可作为战略投送基地的选址点。

本问题的目标函数是要求战略投送基地数量最少。用单元格M26表示选址战略投送基地的总数，它等于决策变量中1的个数，因此，M26=SUM(B26:K26)。

本问题的约束条件包括两个：第一个约束是覆盖约束。即所有候选点均要求有战略投送基地对其实施投送保障，只要候选点与所选的连接关系值之和不小于1。在单元格M15输入SUMPRODUCT(B15:K15,$B$26:$K$26)，它表示节点v1被多少个战略投送基地候选点所覆盖。将上述公式依次复制到单元格M16:M24。第二个约束是单元格B26:K26中的决策变量必须为0-1变量。

2.4在Excel规划求解

在Excel工作表中，设置目标=$M$26为最小值,可变单元格设定为$B$26:$K$26。在约束中设定$B$26:$K$26为0-1整数约束，$M$15:$M$24>=1。选择单纯线性规划方法进行求解，计算结果如图5所示。

求解结果为节点v3和节点v7可作为某战区范围内战略投送基地的选址点，基地3的投送覆盖范围为从节点v1到v5；基地7的覆盖范围为从节点v6到v10。节点v5的数值为2，表明所选定的2个战略投送基地对节点v5均可覆盖。

3　结　语

虽然目前国内外有关设施选址的方法较多，但针对战略投送基地选址问题，既不能完全依靠复杂高深的数学模型,又不能完全凭借工作经验,只有将两者有机结合起来，才能在实践中做出合理的规划决策。本文分析了战略投送基地选址的影响因素，基于整数规划和离散点选址问题，建立了集合覆盖数学模型，探讨了运用Excel工具对战略投送基地进行优化选址问题，实践证明该方法简便可行、快速高效，对做好战略投送基地规划决策具有一定的学术价值和实践意义。

[1]祝刚.区域性国防交通保障基地建设规划研究[D].天津:军事交通学院,2010:33-39.

[2]李景华.运筹学理论、模型与excel求解[M].上海:上海财经大学出版社,2012:5-6.

(编辑：张峰)

Using Excel to Optimize the Selection of Strategic Projection Bases

HAI Jun1, LIU Shunyao2, YANG Jun2

(1.Joint Projection Department, Military Transportation University, Tianjin 300161, China; 2.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China)

To optimize the selection of the strategic projection bases, this paper builds a mathematic model of Set Covering Location Problem on the base of integer programming and dispersed site selection. Excel is used in optimizing the selection and is proved to be feasible, efficient and user-friendly in practice.

strategic projection bases; base selection; Excel

2016-01-04；

2016-03-10.

海军(1963—)，男，博士，教授，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2016.08.002

E234

A

1674-2192(2016)08- 0006- 04