基于全局优化改进混沌粒子群遗传算法的物料平衡数据校正

孙延吉，潘艳秋

（大连理工大学化工与环境生命学部，辽宁 大连 116023）

研究开发

基于全局优化改进混沌粒子群遗传算法的物料平衡数据校正

孙延吉，潘艳秋

（大连理工大学化工与环境生命学部，辽宁 大连 116023）

结合遗传算法（GA）和粒子群算法（PSO）的优点以及混沌运动的特性，提出了加入混沌扰动的混沌粒子群遗传算法（DCPSO-GA），并使用5个高维非线性测试函数考察全局优化混合算法的性能。DCPSO-GA解决了在寻优搜索时出现的停滞现象，扩大了全局优化的搜索空间，丰富了粒子的多样性，且不需要函数梯度信息。测试结果证明，针对本文的5个测试函数DCPSO-GA能找到全局最优解，其收敛速度很快，大大减少了计算量。而且，经过与其他相关算法比较可知，当总的目标函数调用次数较接近或更少时，改进算法不论在计算精度还是收敛速度上，均有很大的提高。并将DCPSO-GA算法应用到重油裂解参数估计和预测中，测试结果证明，其提高了参数估计和预测的准确性，降低了误差，能有效找到全局最优解，收敛速度快，大大减少计算量。

全局优化；改进的混沌粒子群遗传算法；混沌序列；计算精度；收敛速度

化工过程数据校正技术，就是利用数据空间、时间的冗余性，结合各种校正算法剔除原有测量数据中的随机误差和显著误差的影响，并设法预测出未测出变量数据点。所以已测数据的冗余性是化工过程数据校正的基础，采用数据校正之后可以提高实际工业生产过程中数据的精确性和完整性。数据校正技术的基本准则是满足热量平衡、能量平衡和物料平衡的情况下，要求校正值和相应测量数据值的偏差平方和达到最小。从数学的概念分析，就是要求满足一组等式约束方程的最小二乘法解。整个数据校正系统可以用结构图表示，见图 1。为了得到等式约束方程的全局最优最小二乘法解，避免局部最优解，需采用具备全局寻优能力的最优算法进行优化求解方程的全局最优解。

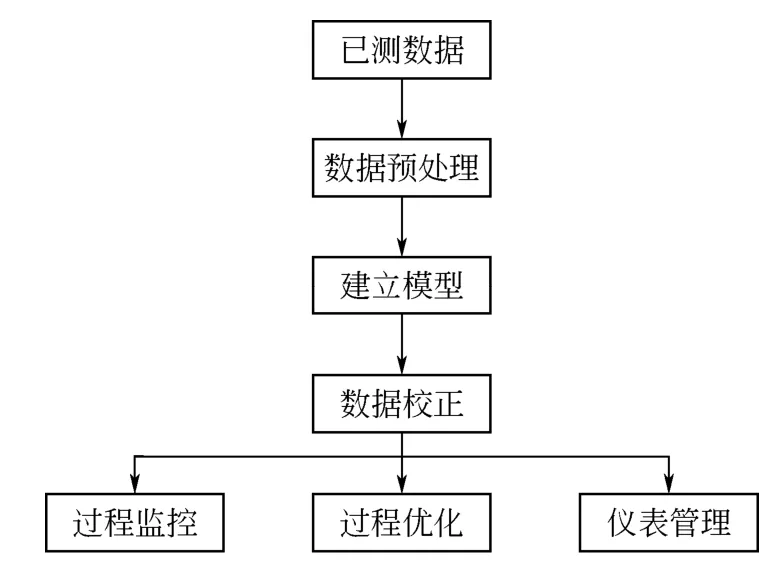
图1　化工过程数据校正技术系统结构图

在科学和工程的众多领域，优化方法虽然得到了广泛应用。然而，对于全局优化问题，研究者尚未找到一种高效通用、并被普遍接受的算法。利用启发式算法求解全局优化问题，成为近年来理论研究和实际应用的热点与趋势。遗传算法（GA）［1］、粒子群算法（PSO）［2］等启发式算法具有并行性、广泛的可适用性和较强的鲁棒性，并且操作比较简单，易于实现，然而一个共同的研究课题是有待于提高算法的全局优化效率。GA是一类基于群体的并行智能搜索算法，它通过染色体共享信息，其全局搜索性能较好，但由于缺乏有效的局部搜索机制，导致GA在接近最优解时收敛缓慢，甚至会出现收敛停滞现象，容易导致收敛精度不高的问题。PSO算法是通过种群中粒子间的合作与竞争行为产生的群体智能优化搜索，保留了基于种群的全局搜索策略，具有记忆性，而且收敛速度快。然而，PSO算法在搜索过程中比较容易陷入局部最优解，从而搜索到全局最优点较困难。

尽管PSO与GA等优化算法［3-5］在计算效率与精度方面都有不同程度的提高，但仍不能满足实际应用的需要。根据PSO和GA两种算法的特点，将PSO与GA算法相结合，能有效扬长避短，发挥GA算法全局搜索能力强、PSO算法收敛速度快的特点，克服PSO算法易陷入局部最优的缺点和GA算法收敛精度不高的缺点。已有很多学者致力于将两种算法结合形成混合算法，并开展了一些研究工作［6-8］。混沌运动作为非线性动力学的一个本质特征，具有遍历性、伪随机性等特点［9］，能在一定范围内按其自身的规律不重复地遍历所有状态。正是利用混沌的这些特性，使其在搜索过程中可以避免陷入局部最优点，很多研究人员将混沌搜索成功地运用到智能优化算法中［10］。通常的混沌优化方法是采用一维混沌映射作为混沌序列发生器，然后将其产生的混沌序列映射到设计空间进行寻优搜索。

本文综合GA和PSO的优点，对GA与PSO的混合算法加以改进，以提高全局优化效率，且为了避免寻优搜索时出现的停滞现象，提出加入混沌扰动的混沌粒子群遗传算法（DCPSO-GA）。为了测试改进算法的计算性能以及讨论搜索到全局最优解精度问题，通过几个高维非线性基准函数对算法进行测试和分析。

1　加混沌扰动的混沌粒子群遗传算法（DCPSO-GA）

GA与PSO两种算法各有利弊，本文在混合算法的基础上加以改进，并引入一维混沌映射产生的混沌序列作为扰动，提出了改进的粒子群遗传算法。Tent混沌序列服从均匀分布［9-12］，全局优化的寻优效果比Logistic映射要好，因此，本文选用Tent映射产生均匀分布的混沌序列，以备改进的混沌粒子群遗传算法之需。

对于无约束优化问题，在混沌优化中混沌变量 z与设计变量Xc之间存在如式（1）所示的映射关系。

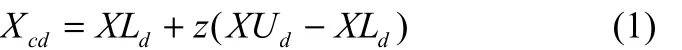
式中，Xcd是Xc的第d个分量；XU与XL是优化设计变量的上界与下界，均是D维向量，d=1，2，…，D。

在 JIA等［13］提出的算法中采用了混沌局部搜索，方程式如式（2）。

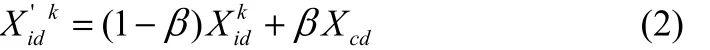
式中，Xcd是通过混沌映射迭代经过式（2）映射到搜索空间［XL，XU］的变量的第d个分量；Xidk是JIA等提出的算法中第k代的第i个个体的第d个分量；Xid'k是由混沌局部搜索产生的新的个体的第 d个分量；β ϵ［0，1］，是收缩系数。那么，将式（1）代入式（2）便得到式（3）。

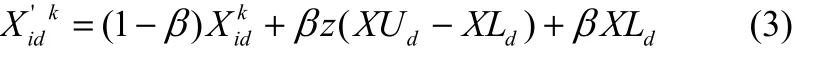
文献［4］中已给出了结论：PSO算法进化过程与粒子的速度无关，并展示了详细证明。本文采用文献［4］中的粒子更新方法，将粒子的速度更新与粒子更新两式合并成一个方程，如式（4）。

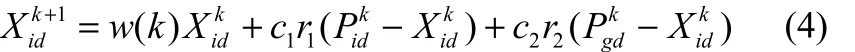
式中，i=1，2，…，n，n为种群个数；d=1，2，…，D；c1与 c2是加速常数；r1与 r2是［0，1］区间的随机数。权重w（k）按更新的效果优于按照线性形式更新的效果，其中wstart为初始惯性权重，wend为迭代至最大次数时的惯性权重，k是当前迭代代数，Tmax是最大迭代代数。

为了改善混合算法的全局优化性能，根据式（3）设计点的迭代形式，结合文献［4］中粒子更新表达式（4），本文提出采用式（5）来更新粒子。

在改进的粒子更新式（5）中，第一项表示粒子的过去对其现在的影响，通过a调节影响程度，a越大，其影响程度越大；第二项表示粒子对当前本身最优位置的靠近，依赖程度取决于参数1-a和混沌变量 z；第三项表示粒子对当前群体最优位置的靠近，依赖程度也取决于1-a和z，实现粒子间的信息共享与合作。从参数a的表达式可以看出，随着进化代数逐渐增加，a呈非线性下降趋势，到进化后期对粒子本身的影响程度减小，而对个体极值与群体极值的影响程度逐渐增大，也即在进化前期局部搜索能力较强，进化后期全局搜索能力增强。在后两项中，混沌变量取值不同，可以增加粒子的多样性，并从不同的方向靠近个体极值与群体极值，避免陷入局部极值点。式中a是缩放因子，m取值越大，收缩的速度越慢，因此m=6比较合适。

粒子群遗传算法在进化过程中，有可能会出现长时间停滞，导致收敛缓慢。为了解决这个问题，在停滞状态下，加入了个体极值的混沌扰动以便跳出局部极值，从而加快收敛。

本文采用停滞代数t作为触发条件，对个体极值Pi进行混沌扰动。极值扰动算子为式（6）。

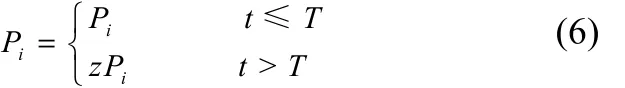
表示若停滞进化代数超过阈值 T，则个体极值按照 Tent映射产生的混沌序列加以扰动。其中，t表示个体极值进化停滞代数；T表示个体极值需要扰动的停滞代数阈值。

加入混沌扰动的粒子群遗传算法（DCPSO-GA）的流程图如图2所示。该算法中粒子的初始化采用的是Tent混沌映射的点序列；交叉、变异、选择操作均采用实数编码机制，其中为了增加粒子的多样性，交叉操作中粒子分别与个体极值交叉和群体极值交叉。

2　模型测试分析

为了测试提出的DCPSO-GA算法性能，并与其他PSO算法比较，选用5个高维非线性基准函数［12-15］进行计算分析，这些函数表达式如式（7）～式（11）。

Sphere函数

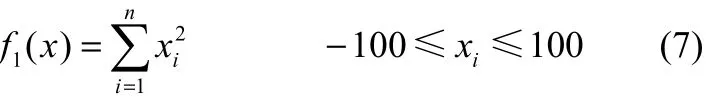
Rosenbrock函数

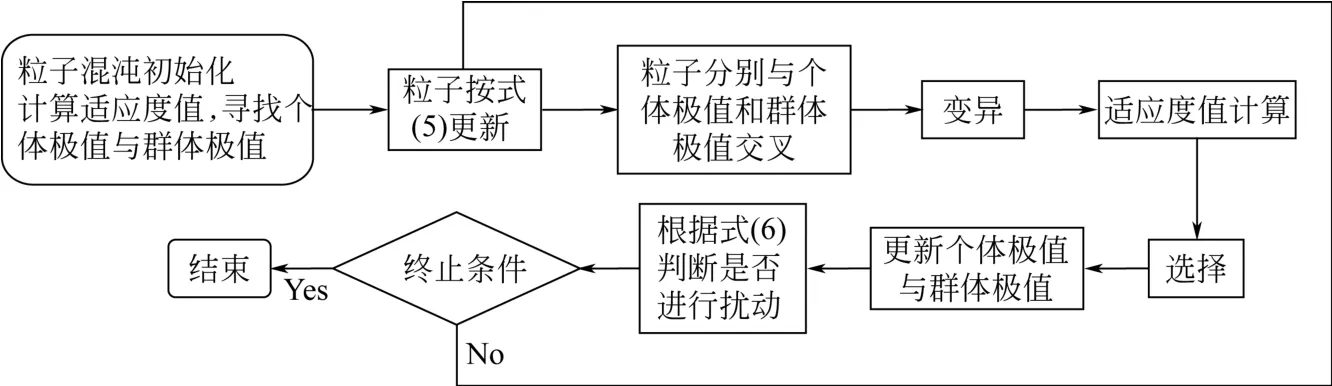
图2　加扰动的混沌粒子群遗传算法流程图

Ackley函数

Griewank函数

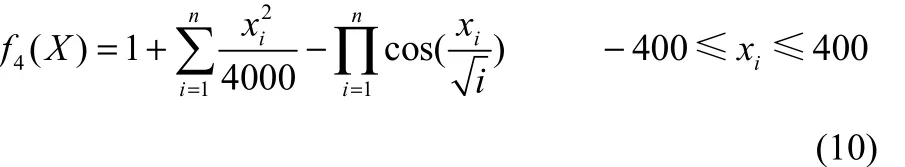
Rastrigrin函数

Sphere和Rosenbrock是单峰函数，其中Sphere函数的最优点是x*=（0，0，…，0），最优值是 f*=0；Rosenbrock函数的最优点x*=（1，1，…，1），最优值是 f*=0。Ackley、Griewank和Rastrigrin 3个函数均是多峰函数，有无穷多个局部极小点，一个全局极小点，3个函数的最优点均是x*=（0，0，…，0），最优值是 f*=0。

当目标函数的维数越高、自变量范围越大、目标精度越高，其优化难度就越大。本文对算法的性能评估采用如下方法：①固定进化代数，评估算法收敛速度与收敛精度；②对测试函数均值和标准差与文献中已有算法的结果进行比较；③固定收敛精度值，评估算法达到该精度所需要的调用目标函数次数均值。

对本次试验参数设置如下：种群规模为 30；最大迭代代数为 500；交叉概率 pc=0.9；变异概率pm=0.1；加速常数c1=c2=2；惯性权重w由0.9减小到 0.4；个体极值需要扰动的停滞代数阈值T=3。图3为几种优化算法对5个维数是30维的函数进行优化测试的进化曲线，本文对函数适应度取以10为底的对数，同时，为了避免真数为0和纵坐标范围过大，对函数的适应度加上10-25作为截止值。

由图3中的5个函数在各算法中的适应度进化曲线可以看出，PSO-GA、CPSO-GA 以及DCPSO-GA解决高维无约束优化问题均好于GA和PSO。其中，混沌粒子群遗传算法CPSO-GA在实现过程中没有加入混沌扰动，粒子群遗传算法PSO-GA的实现过程与CPSO-GA类似，仅在粒子更新时采用式（4）。CPSO-GA和DCPSO-GA的收敛精度和收敛速度最好，均能找到最优解与最优值，甚至可以达到目标的精确解，一般进化代数在 200代以内就能够达到全局最优解，并且 DCPSO-GA跳出了CPSO-GA出现的长期停滞在局部极小点的情况，使收敛速度加快。

图3　f1～f5在几个算法中的适应度进化曲线

图3表明CPSO-GA和DCPSO-GA算法的性能较好。在算法进化过程中，每一代计算出的最优点与最优目标值逐渐向问题的真实解靠近。这是因为粒子在更新时，受到上一代粒子的影响，同时也受到上一代局部最优解和全局最优解的影响。所更新粒子及时纠正局部与全局最优解，最后局部与全局最优解逐渐将问题的真实解靠近，并收敛到问题的真实解。在更新时使用混沌序列，利用混沌的特性进一步增加了粒子的多样性，于是粒子从不同方向向问题的最优解靠近，同时加快了收敛进程。本文提出的算法是PSO与GA相结合作为基础，综合了两种算法的优点，在搜索停滞时又加入混沌扰动，快速改变搜索方向，这也是 DCPSO-GA算法计算准确以及收敛较快的原因。

3　DCPSO-GA在重油热解模型参数估计中的应用

重油热解反应过程中的反应原料为大于 510℃的甲苯可溶物，生成中间重质馏分W后转化为裂解气、轻质馏分及缩合物 L。在等温的条件下，推导出模型反应产率方程式如式（13）。

式中，x和T是自变量；xL为因变量；E为反应的活化能，J/mol；Ep为总热转化反应的活化能，J/mol；EL为中间产物M总生成物L反应的活化能，J/mol；Ew为中间产物M生成馏分W反应的活化能，J/mol；EWL为W转化集总物L反应的活化能，J/mol；ELP为EL、EP之差与R的比值；EWLP为EWL、EP之差与R的比值；KL0为中间产物M生成集总物L反应的频率因子；KW0为中间产物M生成馏分W反应的频率因子；KWL0为馏分W生成集总物L反应的频率因子；nL为中间产物M生成集总物L的反应级数；nW为中间产物M生成馏分W的反应级数；KLP0为KL0与KP0的比值；KWPO为KW0与KP0的比值；KWLPO为KWL0与KP0的比值；KP为总热反应得反应速度常数；KL为中间产物M生成集总物L的反应速度常数；KW为中间产物 M生成馏分 W的反应速度常数；KWL为中间产物M生成馏分W的反应速度常数；KP0为总热反应的频率因子；R为气体常数，R=8.314J/mol。

重油裂解的试验共有 56个观测数据，如表 1所示，每组观测数据有x、T和xL3个数值。其中x表示生成馏分、裂解气体及甲苯不溶物产率之和，T表示反应温度，xL表示裂解气、轻质馏分及缩合产物产率之和。

为了避免系统出现偶然误差测量数据，应用混合交叉检验方法进行检验。将56个重油热解数据样本分为8个组，每个组有7个观测单元，其中1组作为测试样本，其余7组作为建模训练样本。本文分别采用传统常规的PSO和DCPSO-GA算法对重油热解模型中的8个参数进行估计，转化为一个8维的优化问题。

DCPSO-GA算法各个参数的取值与在5个测试函数上的应用所设置的参数相同，其中校正模型中的粒子群规模为 N=200；最大迭代次数为Tmax=1200；搜索空间维数 D=20；惯性权重的取值为 w_max=0.9，w_max=0.3。通过对重油热解模型的仿真试验，对比DCPSO-GA、PSO以及GA算法在重油裂解模型的拟合结果及预测结果，结果如表2所示。

从表 2的结果中可以看出，GA、PSO、DCPSO-GA算法对上述 8个参数的估计值有很大的区别，对于参数ELP，利用GA算法估计出来的值为1112；PSO算法估计出来的值为-1026；DCPSO-GA算法估计出来的值为259。对于参数EWLP的估计值，GA算法的估计值为-5963；PSO算法估计出来的值为-402；DCPSO-GA算法估计出来的值为 1039.1。因此，DCPSO-GA算法在重油热解参数估计中跳出了局部最优解并且进行全局搜索，最终得到了较好的参数估计值。

从表2中还可以发现，DCPSO-GA算法得到的重油模型的拟合误差及预测误差都小于GA和PSO算法，DCPSO-GA算法对模型的拟合程度和预测准确度更高，平均误差要比GA和PSO算法要低。

4　结　论

遗传算法和粒子群优化算法均是基于自然界生物进化理论的随机搜索算法。本文结合GA和PSO的优点以及混沌的特性，提出了混合算法DCPSO-GA，应用 DCPSO-GA对重油热解模型中的 8个参数进行估计，试验结果可以进一步验证DCPSO-GA算法得到的重油热解模型的参数准确性及拟合误差和预测误差均小于传统的PSO和GA算法。在重油裂解模型的参数估计中可以使用本文提出的DCPSO-GA取得良好的结果。

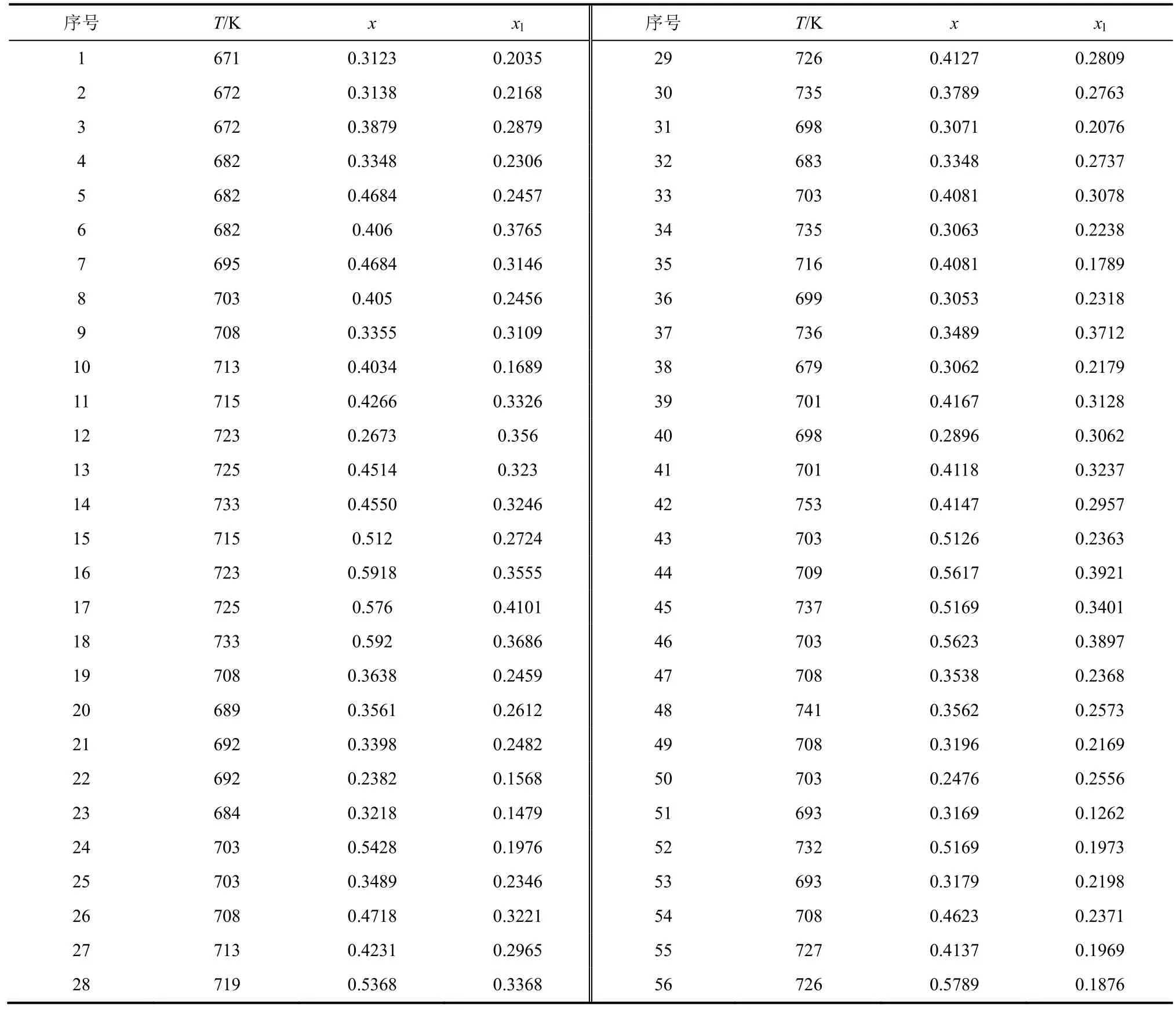
表1　重油裂解的试验观测数据

表2　重油裂解模型参数估计结果

［1］HOLLAND J H.Adaptation in Natural And Artificial System［M］.USA：The University of Michigan Press，1975.

［2］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neutral Networks，Perth，Australia，1995：1942-1948.

［3］蔡良伟，李霞.遗传算法交叉操作的改进［J］.系统工程与电子技术，2006，28（6）：925-928.

［4］胡旺，李志蜀.一种更简化而高效的粒子群优化算法［J］.软件学报，2007，18（4）：861-868.

［5］MAHMOODABADI M J，BAGHERI A，NARIMAN-ZADEH N，et al.A new optimization algorithm based on a combination of particle swarm optimization，convergence and divergence operators for single-objective and multi-objective problems［J］.Engineering Optimization，2012，44（10）：1167-1186.

［6］DOU C H，LIN J S.Improved particle swarm optimization based on genetic algorithm［J］.Advances in Intelligent and Soft Computing，2012，115：149-153.

［7］LIU L Q，LIU C X.A novel combined particle swarm optimization and genetic algorithm MPPT control method for multiple photovoltaic arrays at partial shading［J］.Journal of Energy Resources Technology，2013，135（1）：012002-1-012001-5.

［8］KAO YT，ZAHARA E.A hybrid genetic algorithm and particle swarm optimization for multimodal functions［J］.Applied Soft Computing，2008，8（2）：849-857.

［9］OTT E.Chaos in Dynamical Systems［M］.2nd ed.Cambridge：Cambridge University Press，2002.

［10］YANG D X，LI G，CHENG G D.On the efficiency of chaos optimization algorithms for global optimization［J］.Chaos，Solitons and Fractals，2007，34（4）：1366-1375.

［11］RENATO A K，EDUARDO M，MAURO C.Swarm algorithms with chaotic jumps for optimization of multimodal functions［J］.Engineering Optimization，2011，43（11）：1243-1261.

［12］YANG D X，LIU Z J，ZHOU J L.Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization［J］.Communications in Nonlinear Science and Numerical Simulations，2014，19（4）：1229-1246.

［13］JIA D L，ZHENG G X，KHAN M K.An effective memetic differential evolution algorithm based on chaotic local search［J］.Information Sciences，2011，181（15）：3175-3187.

［14］贾树晋，杜斌.Rosenbrock搜索与动态惯性权重粒子群混合优化算法［J］.控制与决策，2011，26（7）：1060-1064.

［15］范会联，仲元昌.基于信息扩散机制的双子群粒子群优化算法［J］.系统仿真学报，2011，10：2125-2129.

Material balance data correction based on global optimization improved chaos particle swarm genetic algorithms

SUN Yanji，PAN Yanqiu
（Faculty of Chemical，Environmental and Biological Science and Technology，Dalian University of Technology，Dalian 116023，Liaoning，China）

The advantages of genetic algorithm（GA），the particle swarm optimization（PSO）and chaotic motion characteristics are combined in this paper.The chaotic particle swarm genetic algorithm（DCPSO-GA）joined with the chaos perturbing is put forward，and the global optimization performance of the hybrid algorithm are analyzed by 5 high dimensional nonlinear test function.The stagnation phenomenon which appears in the optimal search is solved by DCPSO-GA.The search space of the global optimization is expanded and the diversity of the particle is enriched，while the function gradient information is not required.The global optimal solution can be found by DCPSO-GA for the 5 test function in this paper，and its convergence rate is very fast，greatly reducing the amount of computation.Moreover，it can be known that when the total number of target function calls is close to or less than other related algorithms，the improved algorithm has a great improvement in the calculation accuracy and convergence speed.The DCPSO-GA algorithm is applied to heavy oil cracking parameter estimation and prediction.It can be shown in the test results that the parameter estimation and prediction accuracy can be improved，the error can be reduced，the global optimal solution can be effectively found，the convergence speed can be improved and the amount of calculation can be greatly reduced.

global optimization；the improved chaotic particle swarm genetic algorithm；chaoticsequence；computational precision；rate of convergence

TQ 015

A

1000-6613（2016）09-2663-07

10.16085/j.issn.1000-6613.2016.09.005

2015-12-08；修改稿日期：2016-03-24。

孙延吉（1983—），男，博士研究生，研究方向为化工系统工程。联系人：潘艳秋，教授。E-mail yqpan@dlut.edu.cn。