任意阵列双基地MIMO雷达的半实值MUSIC目标DOD和DOA联合估计

张 秦，张林让，郑桂妹，李兴成（.西安电子科技大学雷达信号处理国家重点实验室，陕西　西安7007；.空军工程大学防空反导学院，陕西　西安7005）

任意阵列双基地MIMO雷达的半实值MUSIC目标DOD和DOA联合估计

张 秦1，2，张林让1，郑桂妹2，李兴成2
（1.西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071；2.空军工程大学防空反导学院，陕西西安710051）

实值处理具有降低高自由度多输入多输出（multiple-input multiple-output，MIMO）雷达角度估计大计算量的优势。但受制于阵列的共轭对称性，对于任意阵列结构的双基地MIMO雷达发射角（direction of departure，DOD）和接收角（direction of arrival，DOA）联合估计，若不做附加的预处理则无法实现实值操作，故将常规阵列实值处理的多重信号分类（m ultiple signal classification，MUSIC）超分辨算法推广至任意阵列结构的双基地MIMO雷达。首先根据MIMO雷达的导向矢量共轭与镜像的对等性，提取接收信号协方差矩阵的实部，并对其进行特征分解得到“目标加倍”的信号子空间及其应对的噪声子空间；然后利用Kronecker积的特性对其进行降维处理，得到搜索区域减半的一维半实值域MUSIC谱，取出目标DOD真值与其镜像代入降维Capon算法来剔除虚拟峰值得到目标DOD估计真值；最后利用特征矢量得到模糊DOA估计值，采用方向余弦差最小范数方法得到目标DOA无模糊估计值。本文算法估计性能与一维搜索复数域MUSIC相当，计算量约降50%，且能够实现DOD 和DOA的自动配对。仿真结果证明了该算法的有效性。

半实值多重信号分类；多输入多输出雷达；任意阵列；发射角估计；接收角估计

网址：www.sys-ele.com

0 引 言

多输入多输出（multiple-input multiple-output，MIMO）雷达由于其发射波形的不一致致使其所拥有独特优势［1 2］，使其在雷达波束形成、检测和参数估计等方面得到了广泛关注［34］，特别是相干MIMO雷达对目标的波达方向等参数估计技术。目前，对于双基地MIMO雷达发射角（direction of departure，DOD）和接收角（direction of arrival，DOA）的联合测量问题，主要从3个方面展开：①如何提高DOD和DOA的估计精度。②如何降低角度估计时所产生的高计算复杂度。③如何实现多目标DOD和DOA角度估计的自动配对。下面对其部分研究内容展开分析。

首先，文献［5］说明了接收信号通过与发射和接收阵元相匹配的匹配滤波器组来分离各正交发射信号，得到更多的虚拟阵元，大大增强了雷达系统自由度，使其较常规相控阵雷达具有更大的虚拟孔径，从而提高波达方向的测量精度。文献［6］基于双基地MIMO雷达，研究利用均匀线阵发射和接收阵列的空域旋转不变性，应用了旋转不变估计技术（estimation of signal parameters via rotational invariance technique，ESP RIT）算法来对目标的DOD和DOA进行联合估计。文献［7－8］利用Kronecker积的特性，推导出了一维搜索Capon算法和多重信号分类（multiple signal classification，M USIC）算法来联合估计DOD和DOA以降低两维搜索算法的计算量。文献［9］对降维M USIC的内在特点进行了分析，提出利用瑞利熵的特点来达到降维的目的，亦能够实现DOD和DOA联合估计的自动配对。文献［10］利用多项式来估计目标的DOD和DOA，进一步降低了计算量。另一方面，文献［11］研究了最大似然方法在双基地MIMO雷达中的应用，以提高DOD和DOA联合估计的精度与稳健性。文献［12］利用联合对角化来扩展阵列以提高阵列的自由度，使其能够估计多于阵元数的目标个数。文献［6-12］均建立在复数域操作，文献［13］将常规阵列的实值处理引入到双基地MIMO雷达的DOD和DOA估计中，在低快拍条件下提高角度的估计精度，且能够实现自动配对。文献［14］利用实值操作来提高多重叠发射子阵MIMO雷达DOD和DOA的估计精度并降低估计计算量。可见实值处理对于MIMO雷达的角度估计有着独特的优势，但是实值处理必须依赖于阵列的共轭对称性，对于均匀线阵组成的发射阵列与接收阵列是可行的，但对于任意阵列则无法实现实值处理。

对于任意阵列构形的双基地MIMO雷达，文献［15-16］利用阵列流形分离技术和特殊的阵列旋转不变性解决了单基地MIMO雷达DOA估计问题和双基地MIMO雷达四维DOD和DOA的联合估计问题。此外，鉴于MUSIC超分辨算法适用于任意阵列，文献［8-9］可直接应用于任意阵列构形的双基地MIMO雷达DOD和DOA的联合估计，但上述方法［8 9，15 16］仍采用复数域处理。

本文将常规任意阵列的实值MUSIC算法推广至双基地MIMO雷达，以实现任意阵列双基地MIMO雷达DOD 和DOA联合估计的实值处理来降低计算量。本文所提半实值MUSIC方法估计性能与复数MUSIC相当，计算量约降50%，且能够实现DOD和DOA联合估计的自动配对。

1 信号模型

双基地MIMO雷达是由M个阵元组成的发射线阵，N个阵元组成的接收线阵，其中发射阵元和接收阵元任意排布，如图1所示，并分别以发射和接收阵列左边第一个阵元为参考点，则发射阵元位置为：Dt=［0，dt，1，…，dt，M-1］，接收阵元位置为：Dr=［0，dr，1，…，dr，N-1］，。则发射阵列的导向矢量可表示为

式中，φ∈［-π/2，π/2］为DOA，并定义u=sinφ为DOA的方向余弦。

图1 任意阵列结构双基地MIMO雷达示意图

这里发射信号采用M个同频但时域正交的窄带波形信号，考虑有K个独立目标存在于同一个距离单元，且发射和接收阵列的孔径远小于目标距离即满足远场条件。接收信号经过N个匹配滤波器组（每组滤波器含M个匹配滤波器，总共则有M·N个匹配滤波器与发射和接收相对应，具体滤波过程见文献［5］），滤波之后对目标的接收信号进行数据重排［5］

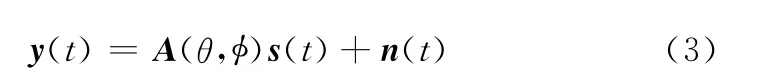
式中，整个MIMO阵列雷达的导向矩阵为A（θ，φ）=［a（θ1，φ1），a（θ2，φ2），…，a（θK，φK）］，其导向矢量a（θk，φk）为发射阵列导向矢量与接收阵列导向矢量的Kronecker积

信号矢量s（t）=［s1（t），s2（t），…，sK（t）］T，sk（t）=βk· ej2πfkt，式中，βk为反射回波复幅度，fk为多普勒频率，上标T表示转置。n（t）是协方差矩阵为M N、均值为0的复高斯白噪声，IM N为M N×M N维单位阵。本文的主要任务就是从式（3）的信号模型来估计该任意阵列双基地MIMO雷达的目标DOD和DOA两维方位角｛θk，φk|k=1，2，…，K｝。

2 常规复数域MUSIC的DOD和DOA联合估计算法

采用最大似然估计方法得到匹配滤波后M N维虚拟阵列的接收信号协方差矩阵：＾R，其中L表示快拍数，上标H表示共轭转置操作。对虚拟阵列接收信号协方差矩阵＾R进行特征值分解得到，其中FS为MN×K维信号子空间，对应于最大K个特征值的特征矢量，剩余特征矢量构成MN×（MN-K）维噪声子空间FN。

根据文献［8］可得两维复数域MUSIC搜索算法可表示为

通过式（5）的搜索谱值，其对应的最大K个峰值，即为目标的DOD和DOA估计值，但其涉及到两维搜索，计算量巨大，可利用文献［8－9］提出的Kronecker积的特性对其进行降维处理。首先利用Kronecker积的性质将a（θ，φ）改写为

根据式（6）将式（5）改写为

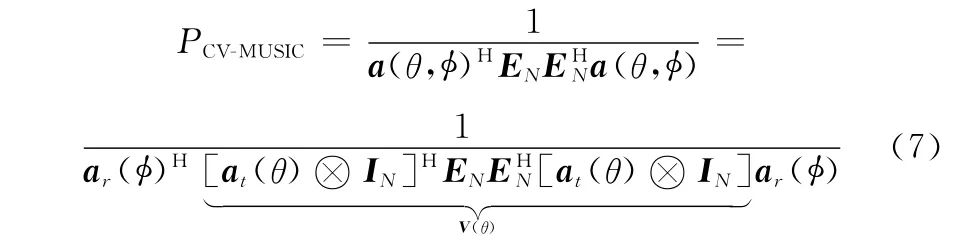
通过文献［8］可知通过式（8）的一维搜索可得到DOD估计值

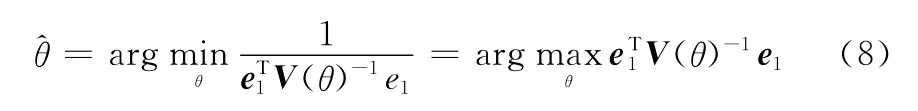
根据式（9）结果，应用最小二乘方法得到目标的DOA估计值。

3 半实值域MUSIC的DOD和DOA联合估计算法

3.1 两维半实值域MUSIC

本文将文献［17］中的常规任意阵列实值MUSIC算法推广至任意阵列双基地MIMO雷达中以达到减少常规复数域MUSIC的DOD和DOA联合估计算法的计算量目的，同时保持自动配对的优点。

下面推导任意阵列双基地MIMO雷达的导向矢量共轭与镜像的对等性。定义噪声子空间及其共轭的交集空间为

式中，上标（*）表示共轭操作。任意阵列双基地MIMO雷达的共轭导向矢量可重构为

根据式（11）将K个目标组成矩阵形式，可得共轭导向矩阵与目标镜像的导向矩阵相等，即A*（θ，φ）=A（-θ，-φ）。此外，总所周知，噪声子空间FN垂直于导向矩阵A（θ，φ），结合式（10）可知交集空间Π垂直于导向矩阵A（θ，φ）及其目标镜像导向矩阵可得常规实值MUSIC一维搜索域减半，对应于两维实值域MUSIC算法，则搜索域减为其搜索表达式为

由文献［17］的定理1可知：交集空间Π与实数空间｛Re（R）-σ2I｝张成相同空间。并由定理1可推导得到交集空间Π可由实值协方差矩阵Re（R）特征分解得到的MN× （M N-2K）维的实数噪声子空间构成，即协方差矩阵Re（R）所对应目标数量加倍的噪声子空间。根据式（12）可知，由于搜索区域减少了3/4且特征分解采用实数操作，该算法计算量大大减少。注意到上述流程中协方差矩阵和式（12）搜索采用复数域处理，特征分解采用实值处理且搜索区域减少，故本文称之为半实值处理。

3.2 一维半实值域MUSIC

但是两维搜索的实值域MUSIC算法所带来的大计算量仍然难以接受。故下面提出利用文献［8-9］的降维方法来对式（12）进行降维处理以进一步减少计算量。

定义式（12）的搜索方程中分母为Θ，即

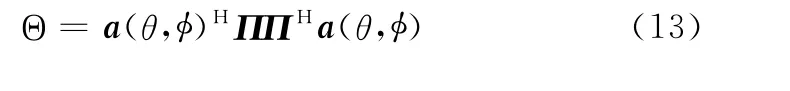
利用Kronecker积的性质将式（13）转化为

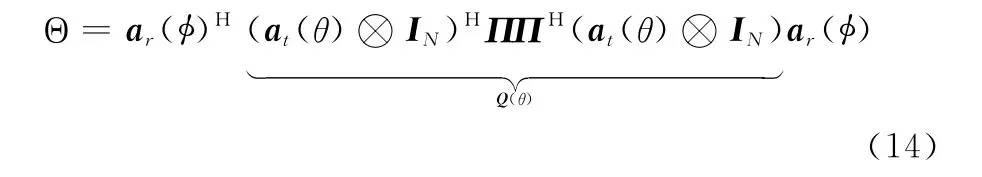
注意到ar（φ）Har（φ）=N，则（14）可转化为

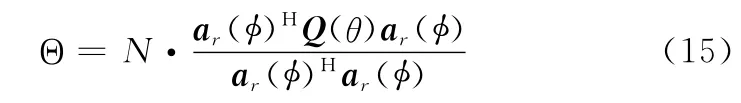
利用Rayleigh-Ritz理论［18］可得到式（15）的最小值为

式中，λmin（θ）为Q（θ）的最小特征值。则目标的DOD估计值可通过如下的一维搜索得到

因采用实值噪声子空间，可知式（17）中的DOD估计值中既包含目标的真实DOD估计值亦包含目标镜像，即｛，…，｝。下面阐述如何利用文献［7］的降维Capon方法来剔除其假峰。

首先给出双基地MIMO雷达的常规两维Capon估计谱

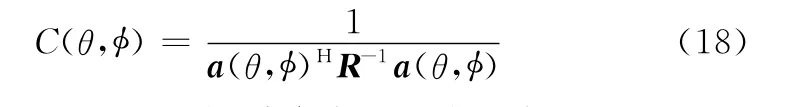
利用Kronecker积的性质将式（18）改写成

利用拉格朗日乘子法可得，通过提取U（θ）-1的第一行第一列元素的最大值可得到DOD的估计值

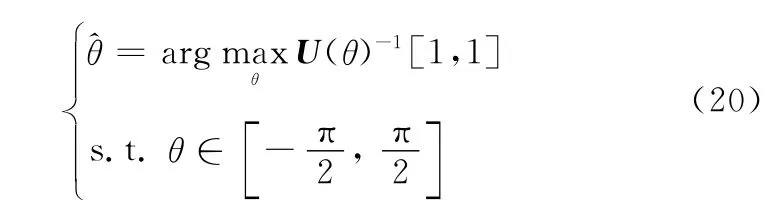
取出真实DOD估计值在式（16）中对应的特征矢量：

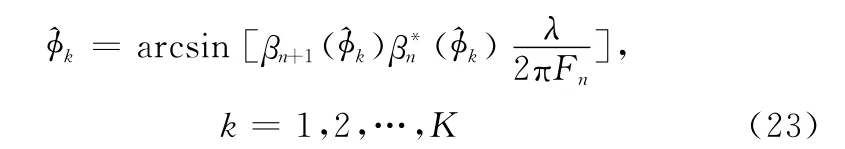
式中，βn（）表示ar（）的第n个元素的角度值即βn（）=∠ar（）。当每个阵元之间间隔均大于半波长，则

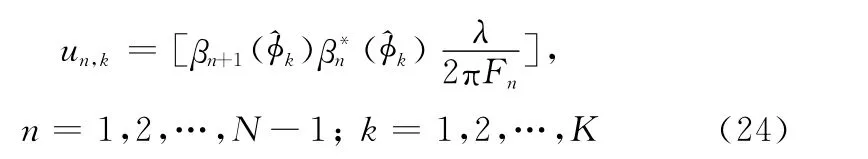
则其周期模糊项为

则第k个目标第n个DOA估计值为

为提高估计精度，对N-1个估计值进行平滑处理得到第k个目标DOA估计值为

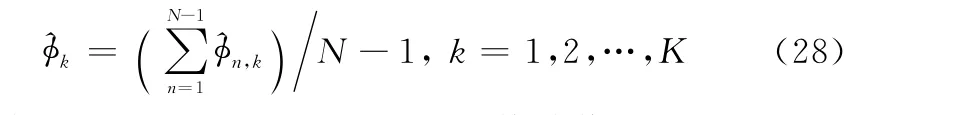
注意式（28）得到的目标DOA的估计值与式（21）的目标DOD估计值是配对的，无需任何额外的配对处理。

3.3 算法流程

本文所提针对任意阵列结构的双基地MIMO雷达的半实数域MSUIC目标DOD和DOA联合估计算法具体流程如下。

步骤1 根据接收快拍数据计算任意阵列双基地MIMO雷达的复数域接收数据协方差矩阵R；

步骤2 取出接收数据协方差矩阵R的实数矩阵Re（R），并对Re（R）进行特征分解得到信号空间维数加倍的实数域噪声子空间Π，维数为：M N×（M N-2K）；

步骤3 根据式（14），利用实数域噪声子空间Π和发射阵列导向矢量at（θ）构造矩阵Q（θ），对Q（θ）进行特征值分解得到其最小特征值λmin（θ），并通过式（17）的一维搜索得到其DOD的真实和镜像估计值｛，…，｝；

步骤4 将该估计值代入式（21）的降维Capon的代价函数剔除其镜像估计值，得到目标的真实DOD估计值；

步骤5 通过式（22）求得真实DOD估计值所对应的特征矢量ar（），即接收阵列导向矢量的估计值；

步骤6 若有相邻阵元的间隔小于半波长，则利用式（23）求得相同目标DOD所对应的DOA估计值。若相邻阵元的间隔均大于半波长，通过式（24）得到方向余弦u的估计值un，k，并通过式（25）至式（28）的拟合解模糊步骤得到其对应相同目标的DOA估计值。

3.4 计算复杂度分析

本文所提半实数域MSUIC算法与常规复数域MUSIC算法均是针对长度为M N的虚拟阵列的输出数据进行处理。

本文算法计算量主要集中在协方差矩阵计算、实数噪声子空间的获取、一维谱搜索、角度解模糊运算。

步骤1 协方差矩阵计算需要O｛（MN）2L｝次复乘运算；

步骤2 实数域噪声子空间Π的获取需要O｛（MN）3/ 4｝次复乘运算；

步骤3 一维谱搜索需要对Q（θ）进行特征值分解，O｛n（N M-K）（M N2+N2）｝次复乘运算，n为搜索点数；

步骤4 需要O｛2K M N3｝次复乘运算；

步骤5 计算量可忽略不计；

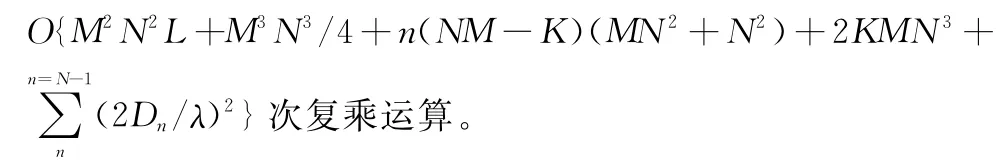
根据文献［9］可得一维复数域MUSIC搜索方法的计算量为：O｛M2N2L+M3N3+2n［（N M-K）（M N2+N2）+ N2］｝次复乘运算。

为直观表示，图2给出其计算量对比图，设发射阵元与接收阵元相等，即M=N。快拍数L=100，搜索间隔为0.01°，则搜索点数n=9×103，阵元间隔均设为Dn=λ （n=1，…，N-1），目标数为K=3。从图2中可看出本文所提半实数域MSUIC算法比常规复数域MUSIC算法计算量约小1/2（注意搜索域虽然减少但是一维搜索仍需其他处理，故计算量大约只降低一半）。

图2 复数域与实数域MUSIC计算量比较

3.5 克拉美罗界

将待估计参数写成矢量形式其对应的费舍尔信息矩阵（Fisherinformation matrix，FIM）为4块-子阵块：

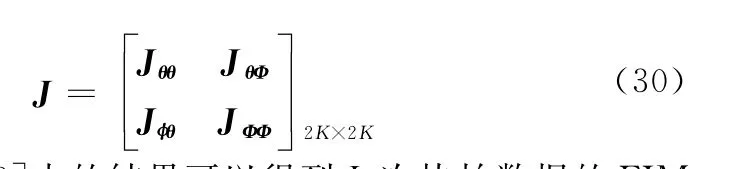
利用文献［19］中的结果可以得到L次快拍数据的FIM子阵块Jhk，（h，k=θ，Φ）的第（i，j）个元素等于

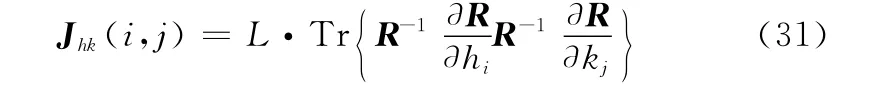
式中，R为MN×MN维虚拟阵列接收数据协方差矩阵：

式中，cr（φk）=josφk［0，dr，1，…，dr，M-1］T；⊙表示矢量对应元素相乘。把式（33）和（34）代入式（31），得到子阵块Jθθ的第（i，j）元素等于

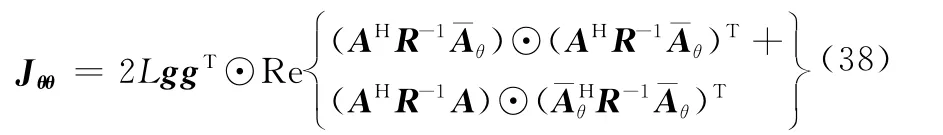
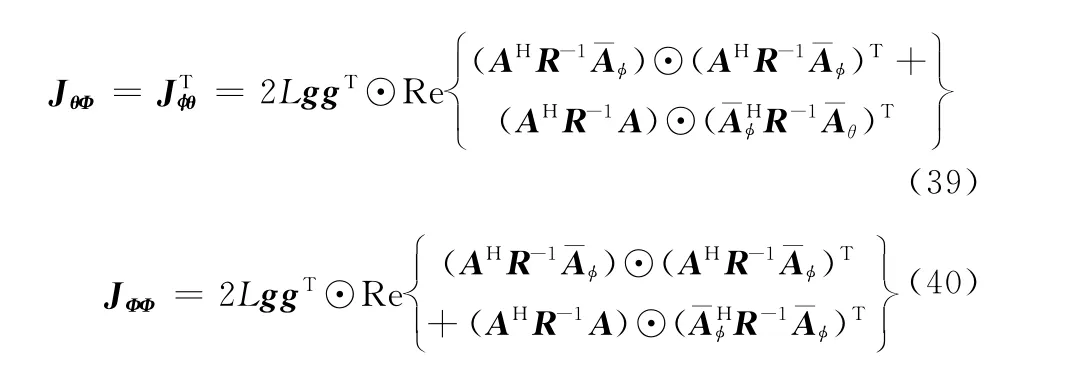
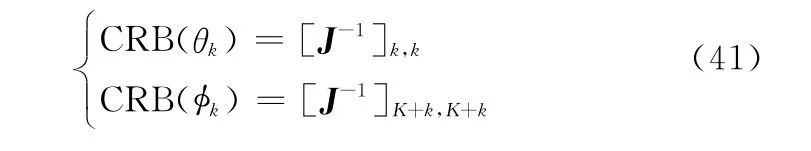
4 计算机仿真结果与分析

考虑一个任意结构阵列双基地MIMO雷达的发射阵元数M=4，接收阵元数N=4，发射阵元与接收阵元位置为：K=3个独立目标存在于同一距离单元，目标DOD为：θ=［-20°，10°，30°］，目标DOA为：=［-30°，5°，20°］，快拍数L=100，信噪比（signal to noise ratio，S N R）S N R=20 dB。图3给出一维半实数域MUSIC算法的DOD估计谱，从图3中可看出该谱存在目标真实估计值与其镜像估计值，验证了本文理论分析的正确性。将该2K个目标真值与镜像代入Capon代价函数计算得到图4的功率谱值，从图4中可看出真值功率远大于镜像功率，故可剔除，与上述理论分析一致。最后得到100次蒙特卡罗试验的DOD和DOA估计值，如图5所示。从图5中可看出该算法能够正确估计出目标DOD和DOA且配对正确，验证了本文算法的正确性。

仿真1 半实数域MUSIC算法的正确性验证

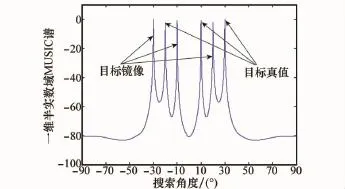
图3 实数域一维MUSIC算法的DOD估计谱

图4 目标真值与镜像的Capon功率谱值

仿真2 估计性能与信噪比关系比较

考虑一个任意结构阵列双基地MIMO雷达的发射阵元数M=5，接收阵元数N=6，发射阵元与接收阵元位置为：目标DOD、 DOA和快拍数与仿真1相同，完成1 000次蒙特卡罗实验，并定义均方根误差（root mean square error，R M SE）为：和DOA估计值，α=｛θ，｝为目标DOD和DOA真实值。考察本文一维半实数域MUSIC算法与文献［8－9］的一维复数域M USIC算法以及CRB的性能比较。图6给出了目标DOD和DOA估计均方根误差随信噪比变化曲线。从图中可以看出，一维半实数域MUSIC估计性能接近一维复数域MUSIC性能，但本文算法的计算量仅约为一维复数域MUSIC的一半，且两种算法的估计性能均接近于RCRB（CRB的求根形式）。

图5 目标DOD和DOA联合估计星座图

图6 参数估计RMSE随SNR变化曲线

仿真3 估计性能与快拍数关系比较

假设S N R=10 dB，其他仿真条件与仿真2相同。图7给出了目标DOD和DOA估计R M SE随快拍数变化曲线。从图7中可得与仿真2相同的结论。

图7 总体R M SE随快拍数变化曲线

5 结 论

本文推导了实值域MUSIC超分辨算法在任意阵列结构双基地MIMO雷达DOD和DOA联合估计中的应用。该算法能够实现搜索空域的减半，计算量约减为复数域MUSIC搜索的一半，且本算法能够实现DOD和DOA估计的自动配对，估计精度接近于复数域MUSIC算法。

［1］Fishler E，H aim ovich A，Blu m R，et al.MIMO radar：an idea w hose time has co me［C］∥Proc.of the IE E E Radar Conference，2004，2：71-78.

［2］Fishler E，H aim ovich A，Blu m R L，et al.Spatial diversity in radars—models and detection performance［J］.IE E E Trans.on Signal Processing，2006，54（3）：823-838.

［3］Li J，Stoica P.MIMO radar with colocated antennas［J］.IE E E Signal Processing Magazine，2007，24（5）：106-114.

［4］Haimovich A，Blu m R，Cimini L.MIMO radar with widely separated antennas［J］.IE E E Signal Processing M agazine，2008，25（1）：116-129.

［5］Bekkerman I，Tabrikian J.Target detection and localization using MIMO radars and sonars［J］.IE E E Trans.on Signal Processing，2006，54（10）：3873-3883.

［6］Chen D F，Chen B X，Qin G D.Angle estimation using ESPRIT in MIMO radar［J］.Electronics Letters，2008，44（12）：770-771.

［7］Zhang X，Xu D.Angle estimation in MIMO radar using reduced-dimension Capon［J］.Electronics Letters，2010，46（12）：860-861.

［8］Zhang X，Xu L，Xu L，et al.DOD and DOA estimation in M IM O radar with reduced-dimension MUSIC［J］.IE E E Com m unications Letters，2010，14（12）：1161-1163.

［9］Xie R，Liu Z，W u J X.Direction finding with auto matic pairing for bistatic MIMO radar［J］.Signal Processing，2012，92（1）：198-203.

［10］Bencheikh M L，W ang Y，He H.Polynomialrootfinding technique for joint DOA DOD estimation in bistatic MIMO radar［J］.Signal Processing，2010，90（9），2723-2730.

［11］Tang B，Tang J，Zhang Y，et al.M axim u m likelihood estimation of DOD and DOA for bistatic MIMO radar［J］.Signal Processing，2013，93（5）：1349-1357.

［12］Xia T.Joint diagonal ization based DOD and DOA estimation for bistatic MIMO radar［J］.Signal Processing，2015，95（3）：159-166.

［13］Zheng G，Chen B，Yang M.U nitary ESPRIT algorithm for bistatic MIMO radar［J］.Electronics Letters，2012，48（3），179－181.

［14］W en C，Shi G.A unitary ESP RIT scheme ofjoint angle estimation for M O TS MIMO radar［J］.Sensors，2014，14（8）：14411 -14422.

［15］Cao Y，Zhang Z，Dai F，et al.Direction of arrival estimation for m onostatic m ultiple-input m ultiple-output radar with arbitrary array structures［J］.IE T Radar Sonar and N avigation，2012，6（7）：679－-686.

［16］Li J，Zhang X.Closed-form blind 2 D-DOD and 2D-DOA estimation for MIMO radar with arbitrary arrays［J］.W ireless Personal Com m unications，2013，69（1）：175-186.

［17］Yan F，Jin M，Liu S，et al.Real-valued MUSIC for efficient direction estimation with arbitrary arrays［J］.IE E E Trans.on Signal Processing，2014，62（6）：1548-1560.

［18］Golub G H，Loan C F.M atrix com putations［M］.3rd ed.Baltim ore：The John H opkins U niversity Press，1996.

［19］Trees H L.Detection，estimation，and modulation theory，part IV：optimum array processing［M］.New York：Wiley，2002.

Joint DOD and DOA estimation for bistatic MIMO radar with arbitrary array using semi-real-valued MUSIC

ZHANG Qin1，2，Z H A N G Lin-rang1，ZHENG Gui-mei2，LI Xing-cheng2
（1.N ational Laboratory of Radar Signal Processing，Xidian University，Xi’an 710071，China；2.Air and Missile Defense College，Air Force Engineering University，Xi’an，710051，China）

Real-valued do main processing has the advantage of reducing the heavy computational complexity for multiple-input multiple-output（MIMO）radar angle estimation with large degrees offreedom.Unfortunately，real-valued do main processing cannot be applied to bistatic MIMO radar with the arbitrary array structure for direction of departure（DOD）and direction of arrival（DOA）estimation except additional pre-processing because the array do not have the characteristic of conjugate symmetry.Therefore，the multiple signal classification（MUSIC）super resolution algorithm for conventional array with the real-valued do main processing extends to the bistatic MIMO radar with the arbitrary array structure.According to the equivalent characteristic between conjugation and image of the steering vector of MIMO radar，the real part of the received signal covariance matrix is firstly extracted and an eigen-decom position is performed to obtain the signal subspace with “double targets”and its corresponding noise subspace.Then the characteristic of Kronecker product is used to reduce the dimension of the process to achieve one dimensional search MUSIC spectrum in the semi-real-valued do main.The true DOD and its images estimations are substituted into reduced-dimensional Capon spectrum to eliminate the peaks of images.Finally，the eigenvectors are utilized to obtain am biguous DOA estimations and the minim u m norm of the direction-cosines difference method is used to disambiguate the DOA estimations.The proposed algorithm has the similar estimation performance and half computational complexity co m pared with the one dimensional search complex do main MUSIC algorithm.Moreover，the proposed algorithm can realize auto-matic pairing between DOAs and DODs.Simulation results verify the effectiveness of the proposed algorith m.

semi-real-valued multiple signal classification（MUSIC）；multiple-input multiple-output（MIMO）radar；arbitrary array；direction of departure（DOD）estimation；direction of arrival（DOA）estimation

TN958

A

10.3969/j.issn.1001-506 X.2016.03.09

1001-506 X（2016）03-0532-07

2015-05-06；

2015-10－12；网络优先出版日期：2015－12-15。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20151215.1629.004.html

国家自然科学基金（61501504）；中国博士后科学基金（2015 M 581097）资助课题

张 秦（1974-），男，副教授，博士研究生，主要研究方向为雷达信号处理、阵列信号处理、精确制导与目标跟踪。

E-mail：kinzh@263.net

张林让（1966-），男，教授，博士研究生导师，主要研究方向为雷达信号处理、阵列信号处理、自适应信号处理和MIMO雷达。

E-mail：lrzhang@xidian.edu.cn

郑桂妹（1987-），男，讲师，博士，主要研究方向为矢量传感器阵列、MIMO阵列雷达信号处理。

E-mail：zhengguimei1987@163.com

李兴成（1978-），男，副教授，博士，主要研究方向为雷达对抗、雷达系统仿真。

E-mail：lixingcheng2008@sina.com