DTI脑网络中枢节点识别方法的比较
靳聪1,林岚1,张柏雯1,赵一平2,吴水才1
DTI脑网络中枢节点识别方法的比较
靳聪1,林岚1,张柏雯1,赵一平2,吴水才1

Hub已成为脑网络分析中一个热点。通过图论分析,可以获取脑网络的拓扑结构特征,并依据这些特征进行hub识别。在对Hub的识别中,识别方法(即网络拓扑特征)的选取是其中的关键的一步。由于全局网络参数不能反映个体节点对于整体网络的贡献,因此局部特征参数被广泛应用于hub识别。当前,有多种hub识别方法在脑网络分析中被应用,但这些方法彼此间的关系还没有确定性的结论。Sporns等人在对动物的研究[8]中采用了模块团、节点度、中心介数、中心度等网络参数。结果显示,猕猴脑网络的hub主要位于V4,FEF,46,7a,TF,5和7b等区域,而猫脑网络的hub主要位于CGp,35,AES,Ia,20a和EPp等区域。他们同时发现,模块团、节点度、中心介数、中心度等识别方法之间存在一定的相关关系。虽然前人对动物hub识别方法的相互关系进行了前期探索,但对于人脑这方面研究还比较少。基于上述研究背景,本研究从hub识别参数的选择入手,探究多种hub识别参数间的关系。
1 实验对象与方法
1.1实验对象与MRI数据采集
75例健康的右利手老年人被用于本研究,他们在实验前均签署知情同意书。受试者年龄范围在50岁至70岁之间,39名女性,36名男性。受试者纳入标准:无精神异常史及其他影响中枢神经系统的疾病,简易精神状态量表(Minimum Mental State Examination,MMSE)检查评分均≥25分,汉密尔顿抑郁评定量表(Hamilton Depression Scale,HAMD)≤10分,实验对象具体特征如表1所示。
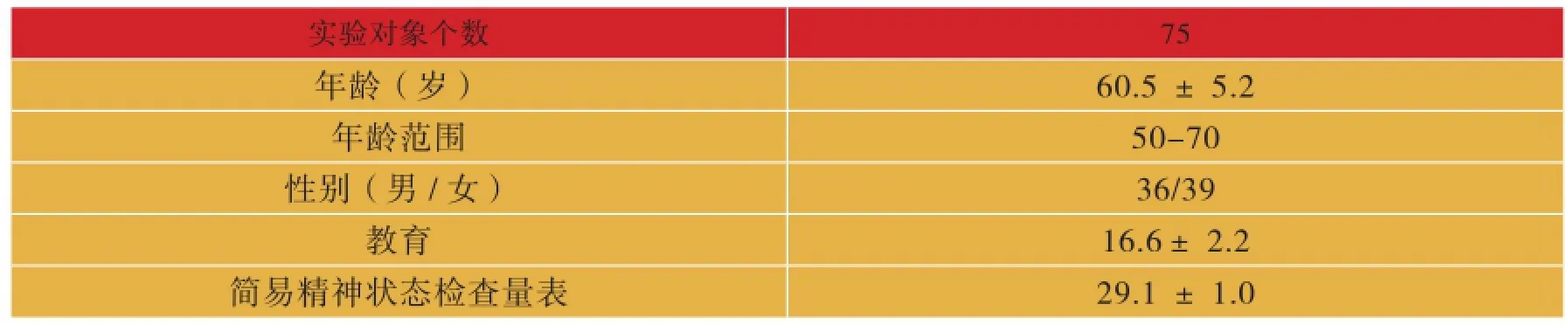
表1 实验对象特征表
所有的磁共振成像数据都是采用3T 高场强GE Signa Excite scanner (General Electric,Milwaukee,WI)扫描获得。数据采集于美国亚利桑那大学附属医院。基于三维扰相梯度回波序列(3D-SPGR)采集204张连续冠状面T1加权像,扫描参数如下:TR 5.3 ms,TE 2.0 ms,TI 500ms,翻转角15°,矩阵:256 x 256,FOV = 256 x 256 mm2,层厚 1mm。DTI扫描采用单次激发自旋回波平面成像(echo-planar imaging, EPI)序列,扫描参数为:8个方向无扩散敏感梯度b值为0 s/mm2,51个方向施加扩散敏感梯度b值为1000 s/mm2,TR 12500ms,TE 71 ms,矩阵:128 x 128,FOV = 250 x 250 mm2,层厚2.6mm。
1.2脑网络构建
在本研究中,我们采用AAL(Anatomical Automatic Labeling,AAL)模板,共划分90个功能区域,每个区域为一个网络节点。DTI影像的预处理及大脑结构网络构建过程通过PANDA软件(a Pipeline for Analysing braiN Diffusion images,http://www.nitrc.org/projects/panda/)实现[9]。首先通过正向和反向配准将AAL模板配准到个体脑空间,完成个体脑网络节点的定义。随后,选用确定性纤维追踪[10]进行纤维束追踪。当FA值>0.2时,纤维束追踪开始计算,当角度阈值(angle threshold)<45°或FA值<0.2时追踪停止[11]。个体空间下模板分割后的AAL影像与白质纤维束进行纤维网络构建,得到二值化的纤维数量连接矩阵[12,13]。大脑白质纤维网络构建基本处理流程如图1所示。
1.3Hub识别
1.3.1Hub识别参数选择
节点度直接反映了和该节点相关联的节点的连接情况。脑网络中的绝大多数节点只有少数连接,而少数节点却可以拥有比较多的连接。节点度较高的节点在很大概率上会是脑网络中的重要的‘交通枢纽’,承担大量的信息传递和转换工作,因而是应用频率较高的hub识别参数。中心介数计算经过某个节点的最短路径的个数,揭示该脑区节点在整个网络的信息传递过程中的重要性,可以从侧面反映出大脑的运行效率,因而是测量节点重要性的另一常见指标。网络脆弱性通过对脑区节点的潜在攻击来衡量节点的重要性。它计算节点去除前后脑网络的全局效率,评估去除该节点对于整个网络影响。除上述单参数识别方法外,多参数识别方法因其全面综合性,也正逐渐被更多的研究者采用。复合参数的构成主要考虑以下因素:(1)复合参数中包含的每一个单参数均具有较高的敏感性;(2)组合应具备综合识别能力,可从不同方面捕捉节点对于网络的贡献;(3)包含的单参数自身具备较高的应用频率。经过甄选,复合参数由节点度,中心介数,聚类系数三个参数组成。
1.3.2Hub识别参数计算
表2和图2展示了识别参数具体的计算公式和注解。
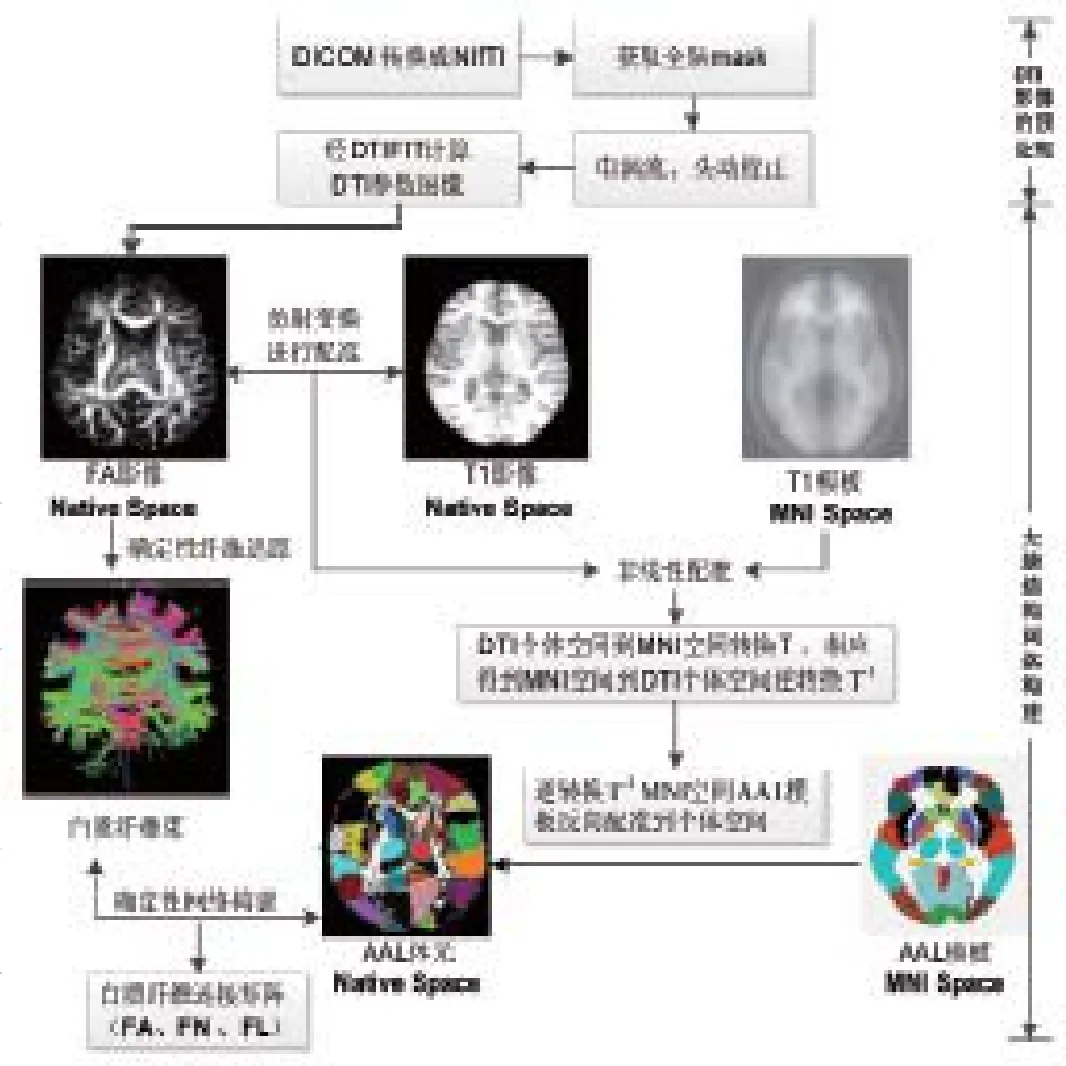
图1 DTI影像预处理及大脑结构网络构建流程图

表2 hub识别参数的计算公式及注解
复合参数中包含度、中心介数和聚类系数三个参数,其中聚类系数揭示节点的邻接节点间的连接情况,因此聚类系数值越低的节点越可能是hub节点。复合参数值的计算中,需要对三个参数值进行加减运算,为降低由于运算引入的误差,这里采用标准化方法对参数值进行处理。
节点排序完成后,将前5%、25%和50%节点挑选出,识别为hub节点。
2 结果
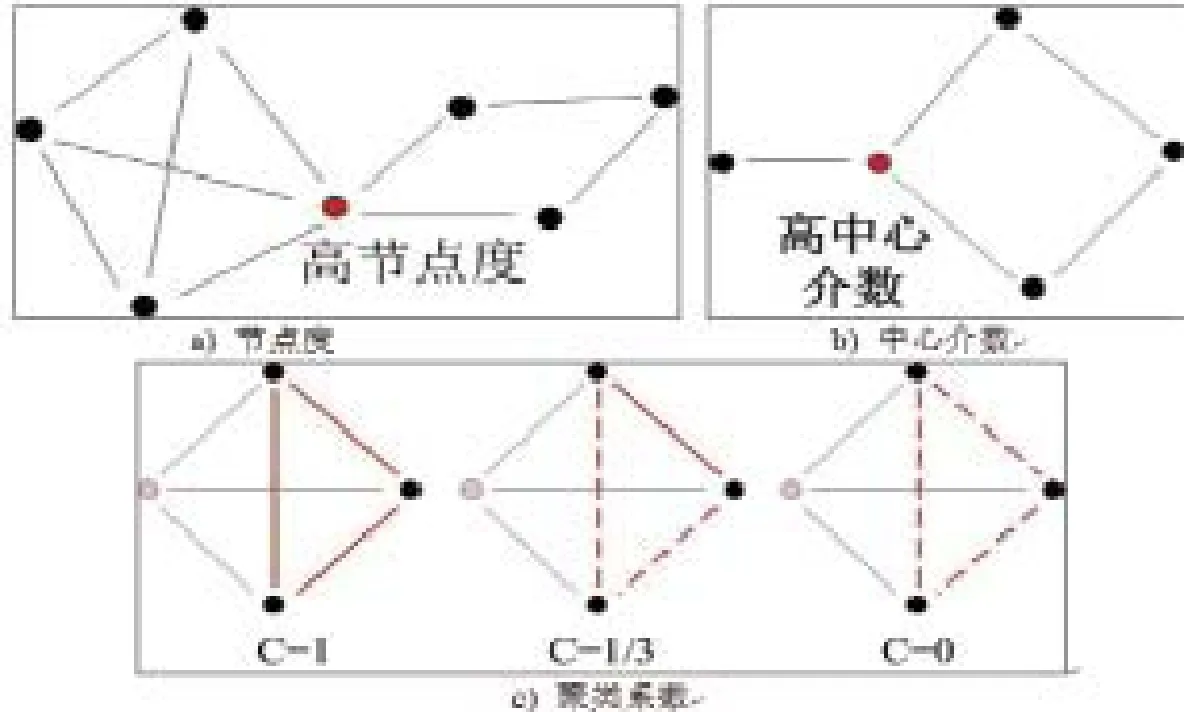
图2 参数解释
图3为大脑网络中的hub分布图。从左到右分别为节点度、中心介数、网络脆弱性和复合参数识别出的hub脑区。红色节点代表5%阈值下识别出的hub脑区,黄色节点代表5%~25%阈值下识别出的hub脑区,蓝色节点代表25~50%阈值下识别出的hub脑区。结果显示,4种识别方法识别出的hub脑区较为一致。4种识别方法可以将一些关键的hub脑区一致性的识别出来,这说明识别方法的差异并不会对hub识别结果造成严重影响。

图3 Hub分布的脑皮层图
我们进一步对不同识别方法识别出的脑区进行排序,图4为不同识别方法识别出的节点的排列顺序。图(a)~图(d)分别对应于节点度、中心介数、网络脆弱性和复合参数计算下的排列情况。
图4 不同识别方法的节点排列
排列结果显示,4种不同的Hub识别方法的结果存在高度的相似性。图5为识别结果的一致性。其中D&B表示节点度与中心介数;D&C表示节点度与复合参数;D&V表示节点度与网络脆弱性;B&C表示中心介数与复合参数;B&V表示中心介数与网络脆弱性;V&C表示网络脆弱性与复合参数。
3 结论

图5 识别结果的一致性
我们选取的4个识别方法各有其代表性。节点度为最常用的hub识别方法,中心介数能够衡量节点在脑网络信息传递中的重要作用,网络脆弱性的应用频率低于节点度和中心介数,但能够从网络效率的角度评估个体节点对于整个网络功能的贡献。此外,我们引入的复合参数,集节点度、中心介数和聚类系数于一体,能够从多特征的角度进行综合性节点重要性的评估。前人的动物实验中,发现了脑连接组hub不同识别方法识别结果的相关性。本章的实验在验证前人研究结果的同时,发现人脑网络特征参数具有更高相关性。在4个识别参数之中,中心介数和复合参数在不同阈值下整体相关性较高,节点度和中心介数在不同阈值下整体相关性较低。我们认为,尽管这些识别参数从数学上并不存在直接关系,但脑网络的脑区划分是依据大脑的解剖结构而实现的。为了实现脑网络的高效性能,Hub节点可能同时具有我们Hub识别的多个特性。Hub节点的重要性并不会由于识别方法的改变而出现大的改变。研究中,不同识别方法识别出的Hub脑区在一定程度上存在可比性。本文研究结果为后人在脑网络Hub方面的进一步研究提供重要的参考依据。

图4 不同识别方法的节点排列
[1]林岚,付振荣,张柏雯等. DTI脑连接组在大脑疾病方面的研究进展[J]. 中国医疗设备, 2015, 30(6): 1-6.
[2]FELLEMAN D J, VAN ESSEN D C. Distributed hierarchical processing in the primate cerebral cortex[J]. Cerebral Cortex, 1991, 1(1): 1-47.
[3]MESULAM M M. From sensation to cognition[J]. Brain A Journal of Neurology, 1998, 121 (6): 1013-1052.
[4]MEYER K, DAMASIO A. Convergence and divergence in a neural architecture for recognition and memory[J]. Trends in Neurosciences, 2009, 32(7): 376-382.
[5]HEUVEL M P, VAN DEN, OLAF S. Rich-club organization of the human connectome[J]. Journal of Neuroscience the Official Journal ofthe Society for Neuroscience, 2011, 31(44): 15775-15786.
[6]CROSSLEY N A, ANDREA M, JESSICA S, et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders[J]. Brain, 2014, 137(Pt 8): 2382-95.
[7]ALBET R, JEONG N, BARABASI A L. Error and attack tolerance of complex networks[J]. Crucitti P, Latora V, Marchiori M, et al. Error and attack tolerance of complex networks[J]. Nature, 2004, 340(1-3):388-394.
[8]SPORNS O, HONEY C J, K TTER R. Identification and Classification of Hubs in Brain Networks[J]. Plos One, 2007, 2(10): e1049-e1049.
[9]CUI Z, ZHONG S, XU P, et al. PANDA: a pipeline toolbox for analyzing brain diffusion images[J]. Frontiers in Human Neuroscience, 2013, 7(6): 42.
[10]MORI S, VAN Zijl P. Fiber tracking: principles and strategies - a technical review[J]. NMR in Biomedicine, 2002, 15(7-8): 468-480.
[11]MORI S, KAUFMANN W E, DAVATZIKOS C, et al. Imaging cortical association using diffusion tensor based tracts in the human brain axonal tracking[J]. Magnetic Resonance in Medicine, 2002, 47(2): 215-223.
[12]林岚,靳聪,付振荣,x等. 健康老年人脑年龄预测:基于尺度子配置模型的大脑连接组分析[J]. 北京工业大学学报, 2015, 41(6):955-960.
[13]Lin L, Jin C, Fu Z,et al. Predicting healthy older adult’s brain age based on structural connectivity networks using artificial neural networks[J]. Comput Methods Programs Biomed., 2016 125: 8-17.

