一种改进的小波阈值去噪方法

李朋，余谅（四川大学计算机学院，成都　610065）

一种改进的小波阈值去噪方法

李朋，余谅
（四川大学计算机学院，成都610065）

0　引言

数字图像在获取、传输及存储的过程中不可避免地会受到各种噪声的污染，这不仅影响图像的视觉效果，还会给对图像的进一步处理和分析带来不利影响。因此，对图像进行去噪处理就显得尤为重要。与传统的去噪方法，如中值滤波、邻域滤波、均值滤波等方法相比，小波变换具有衰减性和波动性，它可以对图像的时域和频域做局部化分析，通过伸缩平移变换达到对信号逐步地进行多尺度细化，最终达到在高频处时间细分，在低频处频率细分的结果。在小波去噪方法中，尤以小波阈值去噪研究最为广泛[1]。

1　小波阈值去噪的原理及步骤

1994年，Donoho和Johnstone提出了基于小波收缩（Wavelet Shrinkage）的去噪方法[2]，他们提出的Vis-uShrink方法就是最早的小波阈值去噪方法。小波所具有的低熵性、良好的时频特性、去相关性等特点[3]，使得小波能够对信号进行多尺度分析，有效地分离图像信号与噪声。

1.1小波阀值去噪的原理

小波阈值去噪的基本原理是，含有噪声的图像信号经小波变换后，有用信号的能量主要集中在少数幅值较大的系数上，而噪声的能量则主要在高频处且小波系数的幅值较小，所以，只要我们能确定一个合适的阈值，对分解得到的小波系数进行阈值量化处理，滤除噪声的小波系数，保留有用信号的系数，就能实现对图像的去噪[4]。小波阈值去噪实现起来比较简单，去噪效果也较理想，因此，它得到了相关研究者的重视，是目前小波去噪方法中研究较为广泛的去噪方法之一。

1.2小波阀值去噪的步骤

利用小波阈值方法对含噪图像进行去噪的一般步骤为：

（1）选择合适的小波并确定分解层次，对含早图像信号进行小波分解，将其变换到小波域，得到个尺度的小波系数。

（2）选择合适的阈值函数和阈值，对高频小波系数进行量化处理。

（3）将经过阈值处理后的小波系数进行小波逆变换，得到去噪后的图像。

很显然，小波阈值去噪方法的关键步骤是选择阈值函数以获得合适的阈值，这样才能达到理想的去噪效果。下一节将介绍小波阈值去噪中阈值函数和阈值的选择方法。

2　小波阈值与阈值函数的选择

2.1常见的阀值

小波阈值去噪中一个比较大的挑战是如何找出一个合适的门限来充当阈值。太小的门限值会使处理后的小波系数保留很多与噪声有关的小波系数，使噪声去除不彻底；而太大的门限值又会使与图像信息有关的小波系数置为零，使图像的重要细节信息丢失。因此，阈值的选取在小波阈值去噪方法中十分重要。下面介绍几种常见的阈值估计方法。

（1）VisuShrink阈值

Donoho和Johnstone在1994年提出了VisuShrink方法[2]，该方法又被称为通用阈值法。它是针对多维独立正态变量联合分布，在维数趋向无穷时得出的结论，在最小最大估计限制下得出的最佳阈值。该阈值被定义为：

其中，σn是噪声的标准差，N是图像中像素的个数。在该阈值估计方法中，相同的阈值被应用在小波分解得到各级小波系数中。尽管通用阈值的估计结果相对平滑，但可能会产生过扼杀现象，在实际应用的效果不太理想。

（2）SureShrink阈值

Donoho和Johnstone在1995年提出了一种基于Stein无偏似然估计 （Stein's Unbiased Risk Estimation，SURE）的软域值估计方法，由此得到的阈值被称为SureShrink阈值[5]。这种方法为不同层级的小波系数设定不同的阈值，SureShrink阈值的目的是使含噪图像与原始图像的均方误差最小。SureShrink阈值的计算方法是先取得给定阈值的似然估计，如式（2）所示；然后再将似然函数最小化，得到所需要的阈值，如式（3）所示。

式（2）中，t是选定的初始阈值，Wj表示来自子带j的小波系数，NW表示各子带Wxy小波系数的个数和。Donoho和Johnstone指出，当小波系数较多时，适用此阈值，当小波系数个数较少时，宜用通用阈值。

（3）BayesShrink阈值

BayesShrink阈值[6]是在假定小波系数服从广义高斯分布（Generalized Gaussian Distribution，GGD）的前提下，利用贝叶斯数学框架、以最小化贝叶斯平均风险为准则来找到各子带详细小波系数。BayesShrink阈值的定义如式（4）所示。

式中，σnoise表示噪声的标准方差，σsignal表示图像信号的标准方差。

2.2常见的阀值函数

在小波阈值去噪方法中，常见的阈值函数主要是硬阈值（Hard threshold）函数和软域值（Soft threshold）函数。

（1）硬阈值函数

硬阈值函数是将绝对值小于或等于阈值的小波系数当作噪声，予以去除，对其作置零处理，将绝对值大于阈值的小波系数予以保留。硬阈值函数的表达式如下式所示。

式中，ω表示小波系数，T表示所选择的阈值，Thard（ω）表示经硬阈值函数量化处理后的小波系数。

（2）软域值函数

软域值函数也是将绝对值小于或等于阈值的小波系数当作噪声，予以去除，即作置零处理，而将绝对值大于阈值的小波系数当作图像信息，并按照一定比例收缩后保留。软域值函数的表达式如下所示。

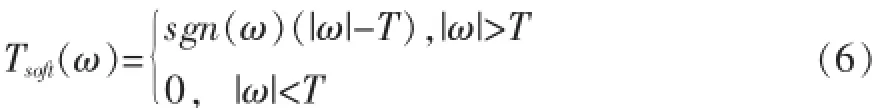
式中，ω表示小波系数，T表示所选择的阈值，Tsoft（ω）表示经硬阈值函数量化处理后的小波系数。函数sgn（ω）是符号函数，它返回变量ω的符号。

一般来说，由于硬阈值函数直接把绝对值小于阈值T的小波系数置为零，因此硬阈值函数会使图像在T和-T处产生不连续现象，但可以较好地保留边缘等局部特征，而软域值函数处理要相对平滑，但会造成边缘模糊等失真现象。

2.3改进的阀值与阀值函数

（1）改进的阈值

考虑到通用阈值会产生“过扼杀”现象等缺点，在参考其他学者研究成果的基础上[7-9]，本文提出了一种改进的阈值选取方法，如下式所示：

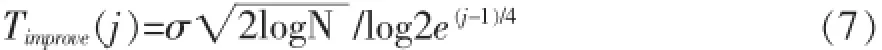
其中，Timprove表示对第j层小波系数所选取的阈值的阈值，σ是噪声的标准差，N是输入的图像中含有的像素个数。j表示小波分解尺度。由式（7）可以看出，当j=1时，所选取的阈值为；当j=2时，所选取的阈值大于j=1时的阈值，而在j>2以后，所选取的阈值又依次减小。之所以这样选择阈值，是因为在小波分解的高频系数中，除了噪声信息外，还有图像的细节信息，因此，为了较多地保留图像的细节信息，本文在对第二层小波系数处理时，所选取的阈值比第一层的阈值增大了；又由于随着小波分解尺度的增大，噪声的幅值逐渐减小，所以当j>2后，选取的阈值又逐渐减小。综上所述，本文所选取的阈值具有一定的自适应性，更符合噪声在不同层次的分布及图像细节信息的实际分布情况，因此，改进后的阈值去噪效果更理想。

（2）改进的阈值函数

针对软域值会造成图像边缘模糊失真等缺点，本文提出了一种改进的阈值方法所选取的阈值函数是如下式所示。

由式（8）可知，与原来的软域值函数相比，改进后的阈值函数的主要变化是对|ω|T的小波系数全置为0，改进后的函数是在原始阈值函数的基础上进行萎缩，且使其具有更高阶，从而使新阈值函数在|ω|=T和|ω|=-T处的图像是连续的且是平滑过渡的，这样，噪声（小波系数）与有用信号（小波系数）之间存就在一个平滑过渡区，从而在一定程度上降低图像的边缘模糊程度。

3　算法仿真

图1　不同阈值去噪方法对高斯噪声去噪的结果比较

实验采用MATLAB（R2010b）自带的图像camera-man.tif进行仿真实验，各种阈值去噪方法所用图片均加入均值为0、方差为0.005的高斯白噪声，用sym4小波函数（由于sym小波有更好的对称性，更适合于图像处理，且能减小图像重构时的相移[10]）对图像进行4层小波分解，然后在不同小波分解层采用不同的阈值去噪方法对小波系数进行处理，最后重构图像。camera-man图片的原始图像、加入高斯噪声的图像、硬阈值去噪图像、软域值去噪图像以及经参考文献[7]、[8]、[9]提出的阈值去噪算法处理后的去噪图像和经本文提出的改进阈值的小波阈值去噪方法处理后的去噪图像如图1（a）-（h）所示。

主观上看，上述小波阈值去噪方法都不能完全去除噪声，但与其它方法相比，本节所提出的基于新阈值的去噪方法在去除图像噪声方面更彻底些，处理后的图像更平滑自然些。

从客观角度评价上述几种基于小波阈值的图像去噪方法（本文中，我们选择所得去噪图像的均方误差和峰值信噪比作为比较内容），由MATLAB计算出的经上述各种阈值去噪方法对含噪图像 （所含噪声是均值为0、方差为0.005的高斯白噪声）进行去噪处理后所得图像的均方误差（MSE）和峰值信噪比（PSNR）如表1所示。

由表1中的数据，我们可以看出，提出的基于小波变换的改进阈值很改进阈值函数去噪方法比上述其他几种方法有明显的优势：去噪更彻底，且对于图像的一些细节信息有更多保留，此外，由该方法的进行去噪处理后所得去噪图像的峰值信噪比也较高，均方误差较小，与原始图像的差别度较小。

表1　不同阈值去噪方法对高斯噪声去噪的MSE和PSNR比

4　结语

本文在分析了小波阈值去噪原理、步骤、阈值选择及软硬阈值函数的基础上，针对常用阈值及软硬阈值函数的不足，提出了改进阈值与改进阈值函数的小波阈值去噪算。实验证明，本文提出去噪方法是有效的，对高斯噪声的去除效果较好。

[1]王蓓，张根耀，李智，王静.基于新阈值函数的小波阈值去噪算法[J].计算机应用，2014，34（5）：1499-1502.

[2]Donoho DL，Johnstone IM.Ideal Spatial Adaptation Via Wavelet Shrinkage[J].Biometrika，1994，81:425-455.

[3]李旭超，朱善安.小波域图像降噪概述[J].中国图象图像学报，2006，11（9）：1201-1209.

[4]程正兴，杨守志，冯晓霞.小波分析的理论算法进展和应用[M].北京，国防工业出版社，2007.

[5]Donoho DL，Johnstone IM.Adapting to Unknown Smoothness Via Wavelet Shrinkage[J].AmericanStaticalAssoc，1995，90（432）: 1200-1224.

[6]Chang S G，Yu B.and Vetterli M.Adaptive Wavelet Thresholding for Image Denoising and Compression[J].IEEE Trans.on Image Proc.，2000，9（9）:1532-1546.

[7]王香菊.基于中值滤波和小波变换的图像去噪方法研究[D].西安科技大学，2008.

[8]杨鑫蕊.改进的小波阈值去噪算法研究[D].哈尔滨理工大学，2014.

[9]蔡德尊.基于小波变换的图像去噪算法研究[D].哈尔滨工业大学，2011.

[10]董长虹，高志，余啸海.MATLAB小波分析工具箱原理与应用[M].北京：国防工业出版社，2004.

Image Noise;Soft and Hard Threshold;Wavelet Transform;Threshold Denoising

An Improved Wavelet Threshold Denoising Method

LI Peng，YU Liang
（College of Computer Science，Sichuan University，Chengdu 610065）

1007-1423（2016）07-0072-05

10.3969/j.issn.1007-1423.2016.07.017

李朋（1988-），男，河南周口人，硕士研究生，研究方向为多媒体技术余谅（1963～），男，四川成都人，副教授、博士，研究方向为多媒体技术

2016-01-26

2016-02-28

数字图像在获取、传输及存储的过程中不可避免地会受到各种噪声的污染，这不仅影响图像的视觉效果，还会给对图像的进一步处理和分析带来不利影响。因此，对图像进行去噪处理就显得尤为重要。针对小波软、硬阈值去噪方法的缺点，提出一种改进的小波阈值去噪方法，该方法的去噪效果要优于软硬、阈值去噪方法和其他一些改进算法。

图像噪声；软硬阈值；小波变换；阈值去噪

In the process of acquisition,transmission and storage,digital image inevitably will be polluted by a variety of noise,this not only influ-ence the visual effect of the image,but also will bring trouble in further processing and analysis of the image.Therefore,it is very impor-tant to remove the noise of the image.For soft and hard threshold wavelet denoising method exist some shortcomings,proposes an im-proved wavelet threshold denoising method,the denoising effect of this method is superior to the hard and soft threshold method and some other improved algorithms.