基于PSO-BP神经网络的矢量水听器的DOA估计*

郭亚强，王　鹏，白艳萍

（中北大学理学院，太原030051）

基于PSO-BP神经网络的矢量水听器的DOA估计*

郭亚强，王鹏*，白艳萍

（中北大学理学院，太原030051）

利用PSO-BP神经网络，研究了基于矢量水听器阵列的水下声源的波达方向估计。首先对阵列协方差矩阵进行实值化和特征分解，然后将信号子空间的基作为PSO-BP神经网络的输入，并作为样本数据进行训练，以降低PSO-BP神经网络的复杂度.最后将测试样本代入PSO-BP神经网络，成功地进行了DOA估计。仿真实验表明，该方法泛化性能好，解决了输入维数过大的问题，并提高了DOA估计精度，具有较强的工程应用价值。

信号处理；DOA估计；信号子空间；BP神经网络；矢量水听器

近年来，矢量水听器是当前热门的研究课题，它的出现弥补了传统标量水听器不能完整接受声场信息的不足。因此，矢量水听器及其信号数据处理是未来的着重点之一，而波达方向估计更是重中之重［1］。波达方向估计DOA（Direction of Arrival）是运用信号处理方法确定信号源所在的方向，解决波达方向估计的方法有两种：一个是建立纯数学模型，通过大量的运算得出结果。例如，MUSIC算法，ESPRIT算法。近些年，这些算法通过改进已经演化成许许多多的算法，并取得丰硕的成果。然而这些算法大多还有以下两个缺点：算法运算量过大，不可能实时实现；环境适应性差，达不到性能的要求。另一个是采用智能学习、“软建模”进行DOA估计。如人工神经网络等。其优点是在建模过程中采用训练样本构造非线性模型。在实际情况中，训练样本可以将多种因素考虑在内，并且该建模方法不需要谱峰搜索，且计算可以快速实现，从而有望应用于实际工程［2］。

在多数文献中，都是将阵列接收信号的协方差矩阵的上三角特征作为神经网络的输入［3-8］。然而由于矢量水听器具有声压与两路振速，其协方差矩阵的上三角特征与声压水听器相比，特征维数增加了许多。如果将多维特征作为神经网络的输入向量，可能将造成权值和阈值的增加，使得构造非线性模型准确度降低，网络预测的精度也会降低。因此，本文首先将接收数据的协方差矩阵实值化并进行分解，然后取信号子空间的基作为神经网络的输入，以此来进行DOA估计，网络模型则选取PSO-BP神经网络。

1　PSO-BP神经网络简介

1.1粒子群算法

粒子群算法是基于一种群体智能的进化算法［9］，它的优点在于简单易实现，同时具有深刻的生物背景。粒子群算法的基本公式为

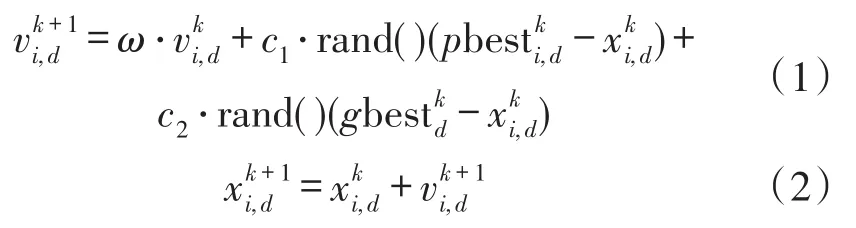
式中，ω为惯性权重；c1和c2为学习因子；rand（）为介于（0，1）的随机数，这几个粒子参数决定了粒子群优化的能力。和分别为粒子i在第k次迭代中第d维的速度和位置，两者都被限定在一定范围内。为粒子i在第d维的个体极值的位置；为群体在第d维的全局极值的位置。

1.2BP神经网络

BP神经网络的整个学习过程中没有引入任何额外参数，它的学习过程完全是根据训练样本对初始权值和阈值的调整，因此初始权值和阈值选取的好坏将会直接影响到最终模型的预测能力［10-11］。对于BP神经网络，它的缺点是算法稳定性差和可靠性低与陷入局部极小值。然而，粒子群算法优化下的BP神经网络模型却可以有效地克服上述缺点。

2　粒子群算法优化下的BP神经网络的DOA估计

本文选取PSO-BP神经网络，因为单独的BP神经网络的泛化性能较差，但用粒子群算法优化后的BP网络却对非线性模型的构建有着突出的能力［12-13］。

2.1矢量水听器的阵列信号模型

考虑N个远场窄带信号源以｛θ1θ2…θN｝的角度入射到M元阵列，阵列的接收信号为

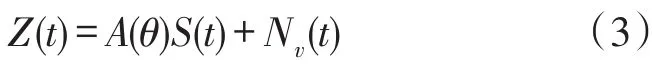
式中，Z（t）是3M×1维的阵列输出矢量，S（t）是N×1维的信号源矢量，Nv（t）是3M×1维的高斯白噪声矢量，且噪声与信号相互独立，A（θ）是矢量水听器阵的信号方向矩阵。

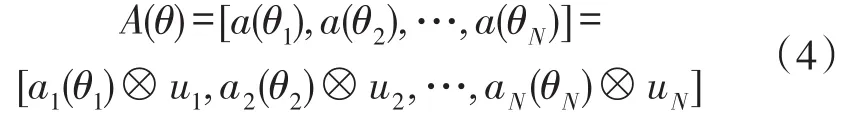
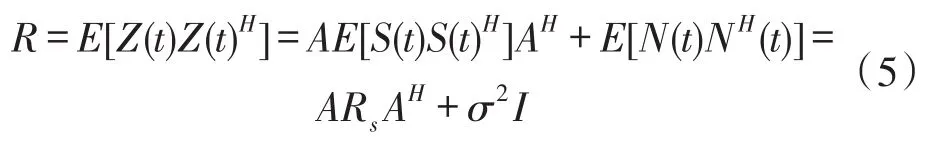
式中，Rs是入射信号的协方差矩阵，σ2是阵列接收噪声的功率，I是归一化下噪声相关矩阵，（·）H代表复共轭转置。

由子空间分解理论，特征分解为是第k个信号的

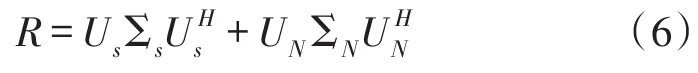
式中，有特征值为λ1≥λ2≥…≥λN≥…≥λ3M，Σs= diag（λ1，λ2，…，λn），Σn=diag（λn+1，λn+2，…，λ3M）。Us是前大N个特征值对应矢量张成的子空间也即信号子空间，有Us=［e1，e2，…，en］，e1，e2，…，en是信号子空间的特征向量；UN是3M-N个特征值对应矢量张成的子空间也即噪声子空间，有Un=［eN+1，eN+2，…，e3M］，eN+1，eN+2，…，e3M是噪声子空间的特征向量。

在实际运算中，考虑到数据长度是有限的，所以阵列协方差矩阵为

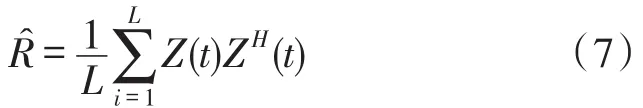
式中，L是快拍数。

2.2基于信号子空间的基的PSO-BP神经网络构建

对于样本的选取，大多数的论文都是选取阵列信号的协方差矩阵的上三角特征作为神经网络输入。而矢量水听器的信号数据包含有声压与两路振速，选取协方差矩阵的上三角会使得输入维数过大，影响估计精度。除此之外，还有一种方法是选取相位差，但相位差易受噪声的影响，且泛化能力较弱。因此，本文选取信号子空间的基作为神经网络的输入，在一定程度上排除了信道噪声的干扰，同时作为网络输入，其节点个数也较少。图1为基于信号子空间的基的PSO-BP神经网络的流程图。

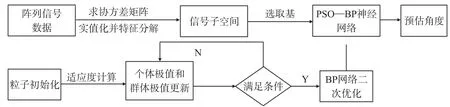
图1　基于信号子空间的PSO-BP神经网络算法流程图

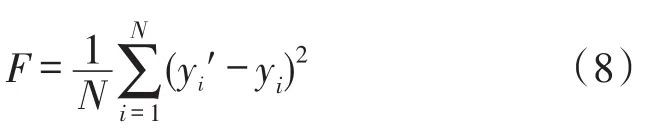
式中，N为训练的样本数，yi为第i个样本的实际值，yi′为第i个样本的模型输出值。

⑥取c1=c2=2，采取线性递减权值策略，惯性权重ω如式（3）所示：

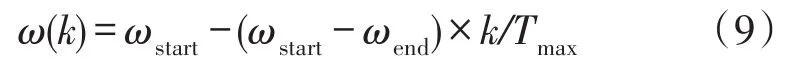
式中，Tmax为最大迭代次数，ωstart为初始惯性权重，k为当前迭代次数，wend为迭代至最大代数时的惯性权重。其中ωstart=0.9，wend=0.4，Tmax=500。

⑦若误差满足预设精度，算法收敛，最后一次迭代的全局最优值就是所求的最优解；若迭代次数未达到最大，算法继续迭代，否则算法终止。

⑧以粒子群算法优化得到的权值和阈值作为BP神经网络权阈值的初始值，再利用BP算法训练权阈值，以此建立DOA估计的预测模型。

算法的具体步骤如下：

①用矢量水听器接收信号数据，求取协方差矩阵。

②将协方差矩阵实值化，并对其分解，求得3M个特征值和3M个特征向量。

③选取信号子空间的基qm作为神经网络的样本，将选取的样本一部分作为训练样本，另一部分作为测试样本，并对神经网络的参数初始化。

④选取粒子的个数为q=50，速度在-1和1之间。假设神经网络的结构为M-N-1，粒子的维数为Num=M×N+N+N+1.

⑤以训练的均方误差函数F作为粒子的适应度评价函数，即

3　仿真实验及性能分析

3.1单信号目标来波方向估计

3.1.1单信号源方向估计精度分析

天线阵列采用均匀5元线阵，选用单个正弦信号源，信噪比为 10 dB，快拍数为500，作 100次Monte-Carlo仿真实验。

训练样本：信号源从-90 到90 每隔0.2 产生一个训练样本，共产生901个训练样本。测试样本：信号源从-90 到90 每隔1 产生一个测试样本，共181个测试样本。图2为本文方法在处理DOA估计的输出预测曲线。

从图2可以看出，在信噪比为10 dB时，本文方法的估计结果与真实值几乎重合，说明本文方法有良好的预测精度。

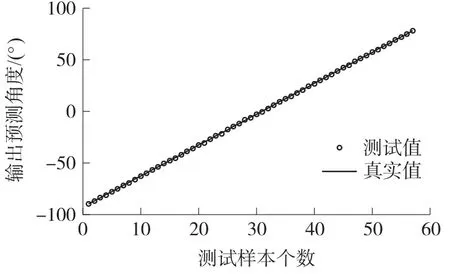
图2　本文方法的DOA估计输出预测曲线

3.1.2不同信噪比下的性能分析

为验证算法在不同信噪比下的有效性，将本文的方法和将协方差作为上三角输入的方法进行对比。仿真条件与上文相同。依次估计本文方法和文献［7］中的方法在信噪比-10 dB到20 dB下，每间隔2 dB的均方根误差。图3为本文方法和文献中的方法在不同信噪比下的均方根误差。

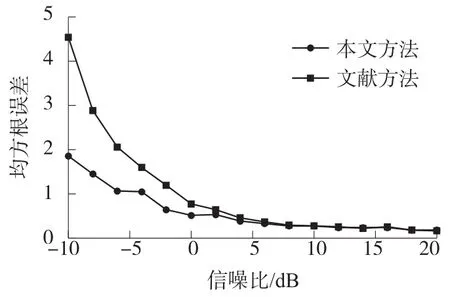
图3　不同信噪比下的均方根误差

从图3看出，在低信噪比下，本文方法的均方根误差远远小于大多数文献中的方法，而在高信噪比下，本文方法和文献［7］方法的均方根误差几乎接近。因此，本文方法在低信噪比下具有良好的精度。

3.2多信号目标来波方向估计

3.2.1多信号源方向估计精度分析

天线阵列采用均匀5元线阵，间距为0.75 m，选用两个正弦信号源，信噪比为10 dB，快拍数为500。

训练样本：两个信号源间隔5 和15 。当间隔为5 时，从-90 到85 每隔0.5 产生一个样本，共产生351个训练样本；当间隔为15 时，从-90 到75 每隔0.5 产生一个样本，共产生331个训练样本，总共产生682个训练样本。

测试样本：两个信号源间隔10 ，从-90 到80每隔1 产生一个测试样本，共171个测试样本，作100次Monte-Carlo仿真。图4为本文方法在多信号下的来波方位估计。

在图4中，预测值和真实值几乎相等，说明本文方法对多信号目标方向估计具有较高的精度。

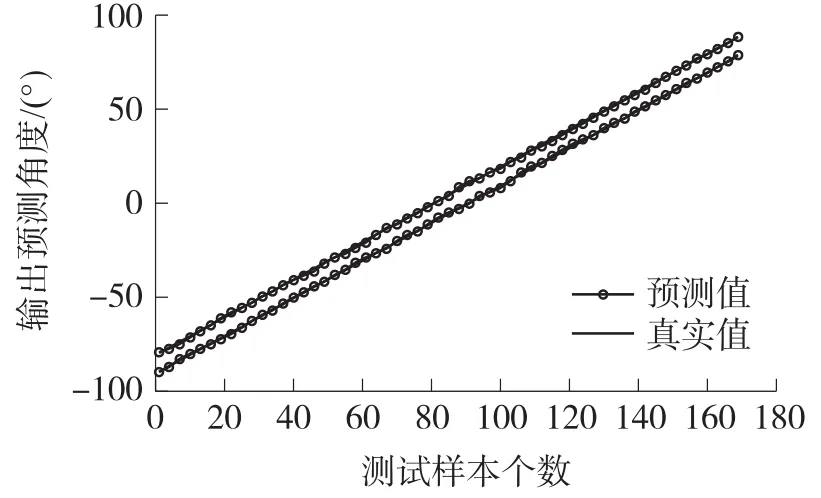
图4　本文方法的DOA估计性能输出曲线

3.2.2不同信噪比下的性能分析

仿真条件与上文相同，依次估计本文方法在信噪比-10 dB到20 dB下，每间隔2 dB的均方根误差。图5为本文方法在不同信噪比下的均方根误差。

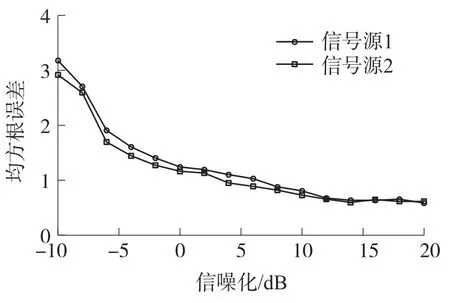
图5　不同信噪比下的均方根误差

从图5中看出，随着信噪比的增大，两个信号源的均方根误差也越来越小，说明本文的方法在不同信号信噪比下具有较高的精度。

3.3算法复杂度比较

在单信号源下，信噪比为10 dB和快拍数为500的情况下，通过统计本文算法和将协方差上三角作为输入的文献算法的运行时间，完成两种算法的复杂度比较，由表1可以看出，本文算法在运行时间和平均绝对误差方面都优于文献［7］算法。

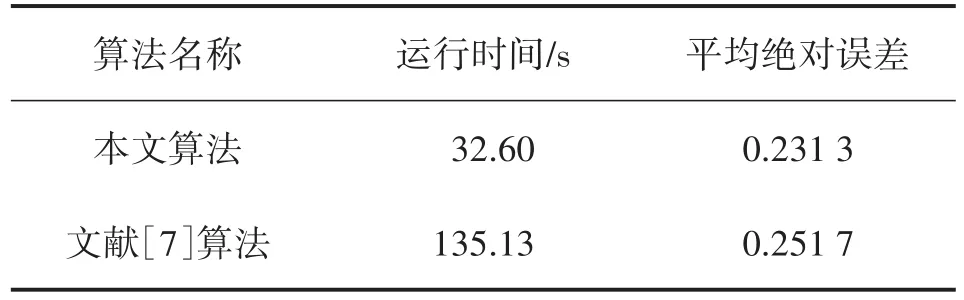
表1　运行时间比较

4　实测实验及性能分析

利用矢量水听器在汾河二库进行了湖试实验，采用五元矢量水听器，固定于船舷一侧，阵元间距0.5 m，置于水下10 m，发射换能器被固定在基阵约90 方位的位置，吊深也为水下10 m，距离基阵约30 m，分别发射了1 kHz、2 kHz、4 kHz的连续单频信号，采样率20 kHz，对接收数据用本文方法进行DOA估计，结果如表2所示。由表2可以看出，本文算法的预测角度和实际角度几乎一致，从而有力地验证了本文算法的有效性。

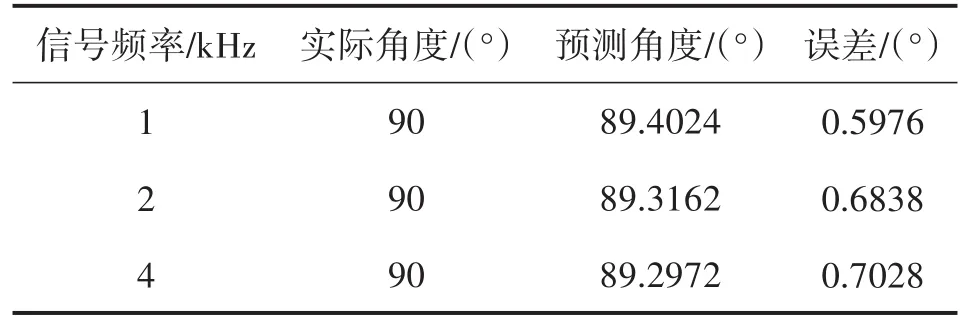
表2　本文算法的DOA估计结果

5　结论

对于矢量水听器的DOA估计问题，本文提出了一种有效的波达角的估计方法，通过运用矢量水听器作为阵列信号接收器，将阵列接收数据求取协方差矩阵并实值化，得到信号子空间的基，将信号子空间的作为神经网络的输入，神经网络则选用粒子群算法优化下的BP神经网络。仿真的结果表明，本文方法具有较好地估计精度。

［1］王鹏.基于MEMS矢量水听器阵列的声目标定向定位技术研究［D］.太原：中北大学，2013.

［2］张旻，李鹏飞.基于分层神经网络的宽频段DOA估计方法［J］.电子与信息学报，2009，31（9）：2118-2122.

［3］Guo W，Qiu T.Performance of RBF Neural Networks for Array Processing in Implusive Noise Environment［J］.Digtial Signal Processing，2008，18（2）：168-178.

［4］林鸿龙，魏贺亮.基于RBF神经网络的非均匀阵列波达方向估计［J］.航天电子对抗，2012，28（2）：52-54.

［5］Wang M，Yang S，Wu S.A RBFNN Approach for DOA Estimation of Ultra Wideband Antenna Array［J］.Neurocomputing，2008，71 （s 4-6）：631-640

［6］何宏，李涛.基于径向基神经网络的波达方向估计算法［J］.徐州工程学院学报，2012，27（03）：6-10.

［7］孟非.基于PSO-BP神经网络的DOA估计方法［J］.电讯技术，2012，52（05）：694-698.

［8］Chen Jinghua，Yi Huiyue，Zhou Xilang.Direction of Arrival Estimation Method with Eigenvector Based Radical Basis Function Neural Network［J］.Journal of Shanghai Jiaotong University，2003，37（3）：372-379.

［9］Kennedy J，Eberhart R.Particle Swarm Optimization［C］//Proceedings of 1995 IEEE International Conference on Neural Networks. Perth，Australia：IEEE，1995：1942-1948.

［10］孔玉静，侯鑫.基于BP神经网络的无线传感器网络路由协议的研究［J］.传感技术学报，2013，26（2）：246-251.

［11］行鸿彦，邹水平，徐伟，等.基于PSO-BP神经网络的湿度传感器温度补偿［J］.传感技术学报，2015，28（6）：864-869.

［12］陈风，田雨波，张贞凯，等.基于GPU的PSO-BP神经网络DOA估计［J］.计算机应用研究，2015，32（10）：2963-2966.

［13］王小川，史峰.MATLAB神经网络43个案例分析［M］.北京：北京航空航天大学出版社，2014：20-33.

郭亚强（1990-），男，山西大同人，在读研究生，主要研究方向为阵列信号处理，模式识别，ttmsen@163.com；

王鹏（1977-），男，山西盂县人，副教授，主要研究方向为水声信号处理，wpmath@nuc.edu.cn。

Direction of Arrival Estimation of Vector Hydrophone Based on PSO-BP Neural Network*

GUO Yaqiang，WANG Peng*，BAI Yanping
（School of Science，North University of China，Taiyuan 030051，China）

The PSO-BP neural network is used to study the DOA estimation of underwater sound source based on vector hydrophone array.At first，the array covariance matrix is used to real-valued and decomposed.Then，the signal subspace is used as the input of the PSO-BP neural network and is trained as the sample data in order to reduce the complexity of PSO-BP neural network.In the end，the test sample is verified in PSO-BP neural network and DOA is successfully estimated.Experimental results show that the method in paper is superior to the common in generalization.The method solves the problem of input dimension that is too large，improves the estimation precision，and has a strong engineering application value.

signal processing；DOA estimation；signal subspace；BP neural network；vector hydrophone

TN911.7

A

1004-1699（2016）08-1229-05

EEACC：723010.3969/j.issn.1004-1699.2016.08.018

项目来源：国家自然科学基金项目（61275120）

2015-12-28修改日期：2016-04-07