带启动时间和休假延迟的Geom/Geom/1排队模型
张 杰
(阜阳师范学院数学与统计学院,安徽 阜阳 236041)
带启动时间和休假延迟的Geom/Geom/1排队模型
张杰
(阜阳师范学院数学与统计学院,安徽阜阳236041)
由于在计算机网络、通讯系统、生产交通领域建模的广泛应用,离散时间休假排队成为近年来应用概率的一个研究热点。考虑带休假延迟和启动时间的Geom/Geom/1多重休假排队系统,运用QBD链和矩阵几何解等工具,给出过程稳态队长分布的具体形式,在此基础上, 推导出平稳状态下队长与逗留时间的随机分解结构,并进一步得到系统在相应状态下的概率和稳态指标的均值。
Geom/Geom/1排队;休假延迟;启动时间;QBD链;矩阵几何解;随机分解
离散时间排队模型由Meisling[1]提出并研究,Hunter[2]系统地给出这类排队的早期分析成果。由于在计算机网络、通讯系统、生产交通领域建模的广泛应用,离散时间休假排队成为近年来应用概率的一个研究热点[3-5]。根据实际应用的特点,文献[6-7]分别将顾客策略和二次可选服务加入Geom/Geom/1休假排队,文献[8-9]研究了带负顾客的情形,文献[10-11]将N控制策略引入Geom/Geom/1多重休假排队系统,并进行了较为深入的研究。
基于节省能源降低成本的考虑,许多系统实际可能需要一个随机的延迟休假时间,休假延迟策略由Leung[12]引入并得到关注[13-14]。考虑到服务台需要休假,而休假期有顾客达到通常是先启动系统,文献[15-16]研究了不同启动机制下的休假排队模型。特别地,文献[17]研究了多重休假的带启动关闭期的Geom/G/1排队,利用嵌入Markov 链的方法,得到了排队指标的随机分解结构。文献[18]考虑了离散时间批到达的情形,文献[19]讨论了连续时间排队的稳态指标,文献[20]运用仿真程序对系统性能指标进行统计分析。
本文在离散时间Geom/Geom/1排队中,提出带启动期及休假延迟的多重休假模型,建立拟生灭链并运用Netus发展的矩阵几何解方法[21],得到系统的平稳队长分布,并阐明了队长和逗留时间的随机分解性质。
1 模型描述
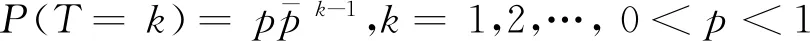
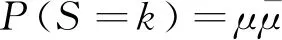

4) 当一次休假结束时,如果系统仍为空,服务台进入多重休假状态。否则,终止休假开始启动服务台,一个随机长度的启动时间A服从参数为α的几何分布,启动期结束后忙期开始;
5) 达到间隔T,休假延迟时间D,启动时间A和休假状态V之间是相互独立的,休假的开始与结束均发生在(n-,n)上。

记Jn=
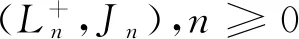
Ω={(0,0),(0,1)}∪{(k,j):k≥1,j=0,1,2}
其中(k,0)(k≥0)表系统有k个顾客且服务台处于休假期,状态(0,1)表示系统在休假延迟期,(k,1) (k≥1)表示服务台位于启动期且其中有k个顾客,(k,2)(k≥1)表示系统内有k个顾客且处于忙期。
其中


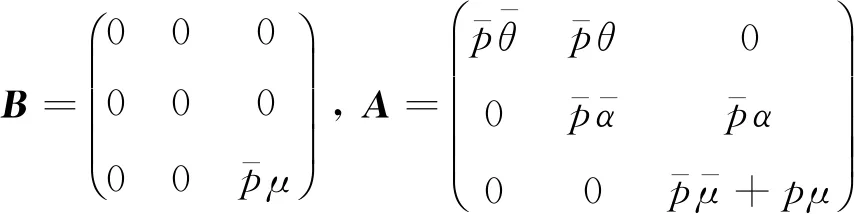

R=R2B+RA+C
(1)
的最小非负解,其中称R为率阵。
引理1若p<μ,则矩阵方程(1)的最小非负解



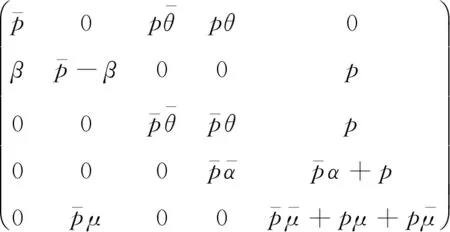
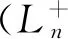
2 稳态队长分布

π0=(π00,π01),πk=(πk0,πk1,πk2)k≥1

定理1若p<μ,则{(L+,J)}的稳态概率分布由(2)式给出
(2)
其中



证明由Neuts,有(πk0,πk1,πk2)=(π10,π11,π12)Rk-1,k≥1,且
(π00,π01,π10,π11,π12)满足(π00,π01,π10,π11,π12)B[R]=(π00,π01,π10,π11,π12).将B[R]代入,得到方程组

记


最后,使用正则条件π0e+π1(I-R)-1e=1,(e是全为1的列向量)可以表出K,
其中(I-R)-1=
由定理1,可得系统平稳状态下服务台处于相应状态的概率分布:





其中

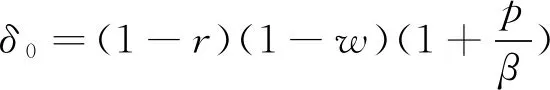


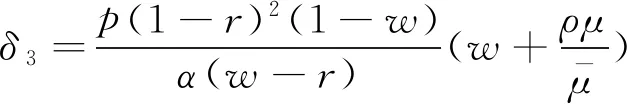

证明由定理1并经过推导,有

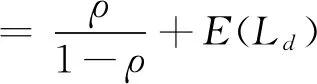
3 逗留时间
定理3在平稳状态下,当p<μ时,带有启动时间和休假延迟的Geom/Geom/1排队模型中顾客的平稳逗留时间W有以下分解:W=W0+Wd,其中W0是经典Geom/Geom/1排队中顾客的平稳逗留时间,附加延迟Wd的LST为






代入上式,得


推论2系统平稳状态时平均逗留时间为
4 数值例子
通过以上分析,得到了系统稳态平均队长和平均逗留时间的表达式。 由图1~4可以看出, 当θ=0.3,p=0.4,μ=0.5,图1~图2中α=0.6,图3~图4中β=0.6时,平均队长与平均逗留时间都是随休假延迟时间D的参数β取值不断增大而逐步增加,随启动时间A的参数α取值的增大先依次递减,后都趋于平稳。

β图1 平均队长E(L+)随β的变化情况

β图2 平均逗留时间E(W)随β的变化情况
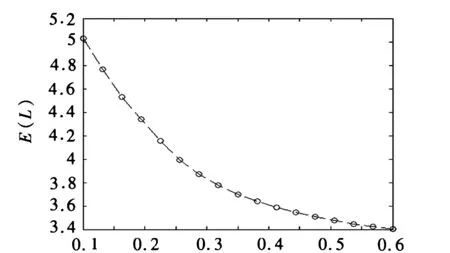
α图3 平均队长E(L+)随α的变化情况

α图4 平均逗留时间E(W)随α的变化情况
5 小结
本文对带启动时间和休假延迟的Geom/Geom/1多重休假排队模型进行了分析,得到模型转移概率阵的经典三对角形式,平稳条件下的队长分布表达式,证明了系统排队指标的随机分解性质,并给出了稳态时系统在相关状态下的概率和附加队长分布与附加延迟LST的具体形式及均值,最后通过数值例子给出了平均队长和逗留时间随休假延迟时间与启动时间的参数的变化情况。这一模型为通信等领域的建模优化提供了理论基础。另外,如何对模型进行推广和完善使其更具实用性,值得进一步的研究。
[1]MEISLINGT.Discretetimequeueingtheory[J].Oper.Res.,1958,6:96-105.
[2]HUNTERJJ.Mathematicaltechniquesofappliedprobabilitydiscrete-timemodels:TechniquesandApplications[M].NewYork:AcademicPress, 1983, 2: 80-95.
[3]田乃硕,徐秀丽,马占友. 离散时间排队论[M].北京:科学出版社,2008,38-46.
[4]彭懿. 负顾客到达的Geo/G/1重试排队系统及在通信网中的应用[J].湖南师范大学(自然科学学报),2015,38(4):68-73.
[5]GAOS,WANGJT,ZHANGDR.Discrete-timeGIx/Geo/1/Nqueuewithnegativecustomersandmultipleworkingvacations[J].JournaloftheKoreanStatisticalSociety,2013,42: 515-528.
[6]马琰,李继红,刘维奇. 多重休假Geo/Geo/1排队的均衡混合门限策略[J].工程数学学报,2013,30(1):19-28.
[7]刘春平,贾礼君,徐秀丽. 具有二次可选服务的Geo/Geo/1工作休假排队 [J].系统科学与数学,2013,33(2):141-149.
[8]朱莎,朱翼隽,王逢佳.带负顾客启动期N策略的Geom/Geom/1工作休假排队[J].系统科学与数学,2012,32(1)36-43.
[9]JIASF,CHENYH.TheGeom/Geom/1queuewithnegativecustomersandsingleworkingvacation[J].应用数学,2012,25(2):304-310.
[10]朱翼隽,潘小春,胡彬.N-策略带启动时间的Geom/Geom/1工作休假排队[J]. 应用数学与计算数学学报, 2010,24(1): 25-34.
[11]朱桂仙,徐德举.N-策略多重工作休假Geom/Geom/1离散时间排队[J]. 首都师范大学学报(自然科学版), 2009, 30(4): 1-5.
[12]LEUNG,KINK.OntheAdditionalDelayinanM/G/1QueuewithGeneralzedVacationsandExhaustiveService[J].Operations.Research, 1992,40: 5 272-5 283.
[13]岳德权,赵玮. 具有延误休假的GI/M/1排队系统[J].运筹学杂志,1994,13(1):33-38.
[14]DENGYL,BRAUNWJ,ZHAOYQ.M/M/1queueingsystemwithdelayedcontrolledvacation[J],0RTransactions,1999,3(4): 17-30.
[15]唐应辉,李沁洪,余妙.休假结束立即启动的M/G/1单重休假排队系统分析[J].应用数学,2014,27(2):447-456.
[16]魏瑛源,唐应辉. 带启动时间的延迟N——策略Geo/G/1排队系统的队长分布及容量的优化设计[J].高校应用数学学报,2013,28(4):391-405.
[17]马占友,徐秀丽,田乃硕.多重休假的带启动-关闭期的Geom/G/1 排队[J]. 运筹与管理,2004, 13(5): 21-25.
[18]刘亚贞,田乃硕,修春.多重休假的带启动期和关闭期的Geomx/G/1排队[J].长春大学学报,2009,19(4)42-44.
[19]李沛,徐秀丽,曹学云,等.带启动-关闭期和N策略的多重休假M/G/1排队[J]. 数学的实践与认识,2011,41(13):145-149.
[20]陈利,杨蕊,马占友. 对多重休假的带启动——关闭期的Geom/G/1排队性能的仿真实验分析 [J]. 山东大学学报(理学版),2015,50(8):46-50.
[21]NETUSM.Matrix-geometricsolutionsinstochasticmodels[M].Baltimore:TheJohnsHopkinsUniversityPress, 1981: 80-120.
[22]KEILSONJ,SERVILD.AdistributionalformofLittle’slaw[J].OperationsResearchLetters,1988,7 (5) 223-227.
(责任编辑:何学华,吴晓红)
The Geom/Geom/1 Queue Model with Setup Time and Delayed Vacation
ZHANG Jie
(School of Mathematics and Statistics, Fuyang Teachers College, Fuyang, Anhui 236041,China)
This paper considers a Geom/Geom/1 queueing system with multiple vacation, delayed vacation and setup time. By applying quasi-birth-death chain and matrix-geometric solution method, the analytic expression of the stationary queue length is given. Meanwhile, it has demonstrated the stochastic decomposition structures of the stationary queue length and sojourn time. Moreover, expectation of stationary indices, the steady state probabilities that the system in vacation delay, vacation period, setup time and busy period are calculated respectively.
Geom/Geom/1 queue;delayed vacation;setup time;quasi birth and death chain ;matrix-geometric solution;stochastic decomposition
2016-01-16
国家特色专业基金资助项目(TS11496);安徽省高校自然科学研究基金资助项目(KJ2014ZD21,KJ2015A182,KJ2015A191);阜阳师范学院自然科学研究基金资助项目;教学团队基金资助(2015FSKJ07,2014JXTD01)
张杰(1981-),女,安徽淮南人,讲师,硕士,研究方向:随机运筹学。
O226
A
1672-1098(2016)03-0032-06

