基于重叠节点的社会网络最短路径算法

朱恺骋,　程　华

(华东理工大学信息科学与工程学院,上海 200237)



基于重叠节点的社会网络最短路径算法

朱恺骋,程华

(华东理工大学信息科学与工程学院,上海 200237)

通过路径发现和分析可以挖掘社会网络中人与人之间的关系及其连接特性,特别是在犯罪网络的应用中具有重要意义。通过社区发现算法获得社区间的重叠节点,并构造目标网络的分层网络模型; 基于社会网络的高聚集系数特性及幂律分布拓扑特征,提出了基于重叠节点的分层网络路径发现(HOLN)算法,以核心节点距离代替社区间距,优化路径搜索方向; 优先搜索重叠节点,简化对节点的遍历,实现源与目标间最短路径的快速发现。实验结果表明,本文提出的HOLN算法在计算精度和运行效率上都有令人满意的表现。

社会网络; 最短路径; 重叠节点; 分层网络

面向社会网络的挖掘和分析是目前的研究热点,通过路径的发现和分析可以挖掘社会网络中人与人之间的关系及其连接特点,特别是在恐怖袭击网络、犯罪网络中的应用中具有重要意义。最短路径算法是路径发现的基础算法,在一定网络规模下具有高精度、高复杂度的特点。互联网环境下社会网络往往具有较大的规模,导致经典算法由于计算复杂度急剧升高难以有效运用,可采用优化算法结构的方法降低算法的计算复杂度或采用启发式方法限定搜索空间获得近似计算最短路径。

CDZ算法[1]基于实际网络的拓扑特征进行算法结构优化,利用了局部中心性和区域中心点距离的最短路径近似计算,路径计算的时间复杂度降为O(e+nlgn),但预处理的时间开销较大; LBFS算法[2]根据最优覆盖策略选择路标集合,广度优先遍历计算路标子网络中节点到路标的路径,算法运算效率很高,但在最优覆盖策略中利用复杂度较高的Dijkstra算法使得算法消耗的预处理时间随着网络规模的扩大呈线性增长; 基于子图引导的路径发现算法[3]采用分层引导的启发式思想缩小交通网络的搜索空间,降低了算法复杂度,但算法通过网络中节点的坐标引导搜索方向,无法运用在抽象网络中。

根据分层策略能够抑制算法随网络规模扩大而非线性增长的特性,本文提出了基于重叠节点的分层网络路径(HOLN)算法。首先将目标网络分层降解得到分层网络及重叠节点; 然后利用社会网络的高聚集性和幂律分布特征,以核心节点距离代替社区间距,通过社区间距引导搜索方向; 在路径搜索中对重叠节点进行优先搜索,从而简化对节点的遍历,达到提高搜索效率和精度的目的。

1　基于重叠节点的分层网络路径发现(HOLN)算法

1.1基于LFM算法的网络层次划分

社会网络是由个人或组织作为节点构成的一种网络结构,经由社会关系,把个人或组织串联起来。社会网络的社区结构是根据节点之间的距离或相似度划分的若干个群组,同一个群组内节点之间的连接比不同群组节点之间的连接密集,而不同社区之间往往有重叠节点[4],是网络的关键“桥梁”,节点间的最短路径在跨越不同社区时经过重叠节点的可能性非常大,因此本文将重叠节点作为路径发现中优先搜索的节点。

LFM算法[5]既能发现重叠点又能将网络进行层次结构划分,因此本文采用LFM算法发现社区。LFM算法计算节点的适应度,其函数定义为

(1)

(2)

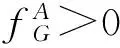
分层网络构建算法步骤如下:

第1阶段,基于LFM的社区划分与重叠节点发现。

(1) ∀v∈V,任取节点v作为初始社区G;

(2) 计算社区G的所有邻居节点的适应度,适应度大于0的节点加入到社区G中,若社区G的全部邻居节点的适应度都小于0,进行第(4)步;

(3) 计算社区G内每1个节点的适应度,若内有适应度小于0的节点,将该节点从社区中移除;

第2阶段,社区发现后的层次网络重构。基于第1阶段发现的社区,构建相应的抽象网络,如图1所示。按照社区划分时节点加入社区Gn的顺序,从初始节点v开始,并入社区中适应度最大的中心节点,并将原来指向节点v的连接修正为指向中心节点,直到社区中节点都指向中心节点,该社区便以中心节点为核心聚合成更高层次中的节点。

两个阶段交替地进行,直到网络中所有节点都找到所属的社区并聚合,由此得到实际网络的层次结构及社区的重叠节点集合。

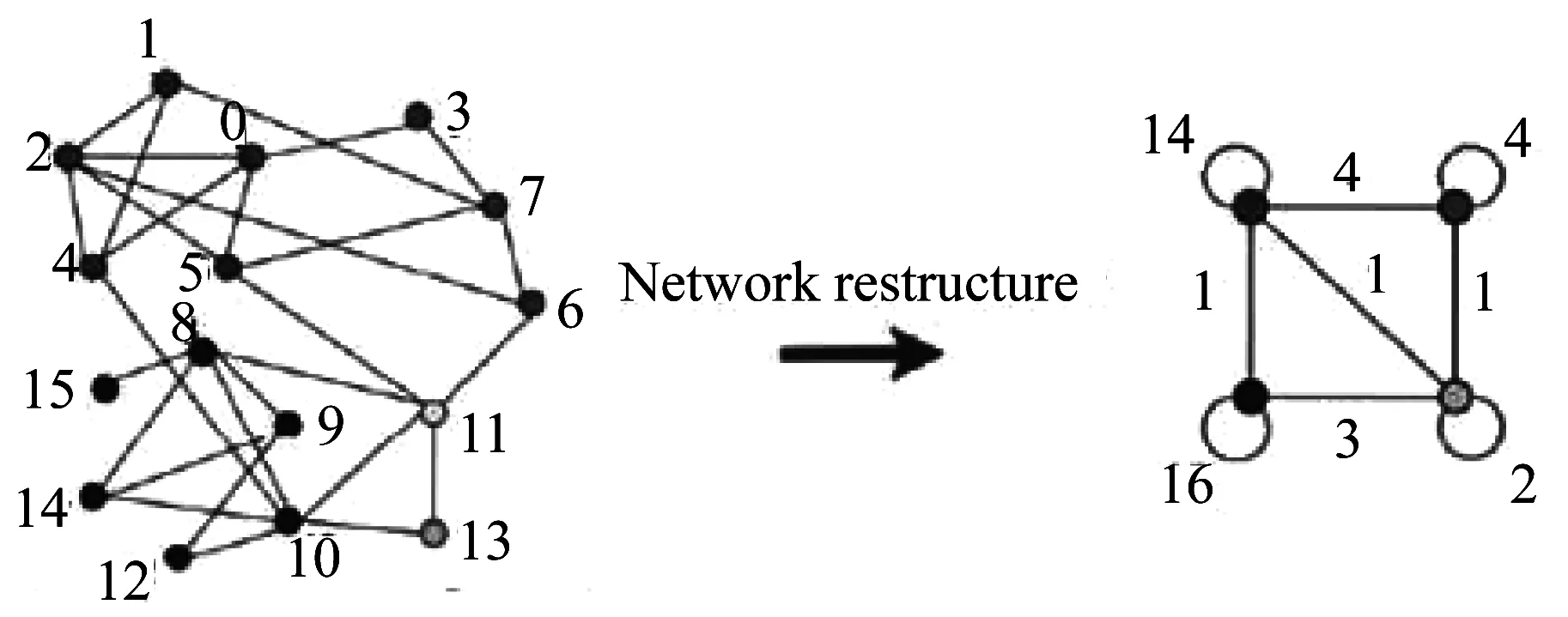
图1　社区发现后的网络重构Fig.1　Network restructure after community discovery

1.2社区间距计算

真实网络中大部分节点在小范围内相互连接,呈现出高聚集性以及幂律分布特征[6],即存在少量高适应度的中心节点及大量低适应度的普通节点[7]。CDZ算法论证了复杂网络中,任意节点之间的最短路径有极大概率经过中心节点。利用该结论,可通过计算节点到中心节点的距离获得节点间的近似位置,在此基础上聚合构造的抽象网络,由社区对中心节点之间的距离代替社区之间的距离,迭代计算得到社区间距。

(3)

缩放比例Li是低层社区聚合成高层网络后社区半径之比[8],取每个分层的社区中适应度最大的节点作为中心节点c,定义第1级层次网络的半径r1为初始网络社区中其余所有节点到中心节点的距离和的平均值,即

(4)

每个分层都是上一级网络以相同的尺度聚合而来,可推得

(5)

定义r0=1,由式(4)、式(5)可得

(6)

式中k是最高级网络聚合的层数。图2为层次网络聚合示意图,体现了层次间的关系,第i级层次网络的中心节点csi和cti分别对应第i+1级层次网络中的普通节点si+1和ti+1。

1.3分层重叠网络的路径引导算法

利用社区间距及重叠节点信息作为启发式引导,采用双向搜索模式,在当前访问的正向和反向社区的邻居中挑选若干对距离较近的社区作为下次访问的对象,使正向和反向搜索快速逼近。

图2　层次网络聚合Fig.2　Hierarchical network aggregation

图3为路径构造示意图。图中s和t为初始点与目标点,p36、p47是社区间的重叠节点。HOLN路径引导算法分为两个阶段:

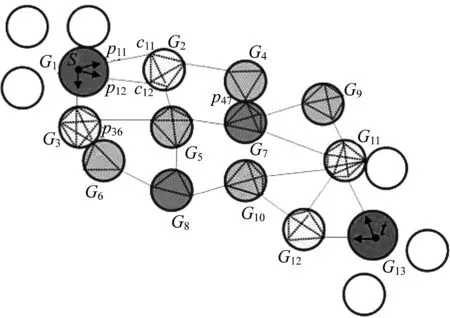
图3　路径构造示意图Fig.3　Scheme of path structure

(1)选择社区对。找出初始点s与目标点t所属的源、目标社区对Gs和Gt作为当前社区对,选取从Gs的邻居社区到Gt邻居社区的α对距离最近的社区对,筛选出距离小于其父辈社区间距β倍的社区,列为下次访问的社区对。

(2)构造路径。以正向搜索为例,步骤如下:

①在分层网络中判断当前社区Gs到下次访问G2是否存在重叠节点,若存在,将其标记为点p(若有多个则标为p1,p2,…)并跳到步骤③,若不存在,则执行步骤②;

②找出从当前社区到下次访问的社区之间的边(图3中的p11、c11和p12、c12),找到它们在父辈社区中的端点,即p11、p12;

③由Dijkstra算法计算从初始点s到所有标记点的最短路径,将其与之前获取的路径拼接起来,同时将重叠点或非重叠点(由步骤①中是否找到重叠节点决定)作为下一段路径的拼接点。

重复步骤①～③进行路径的构造与拼接。

两个阶段交替进行。算法中反向搜索和正向搜索类似,改为从目标社区Gt发出。当正向、反向搜索相遇,即在正向、反向搜索中出现了相同社区或者直接相邻的社区对时,完成最后的路径拼接,此时终止算法的执行,在多条路径中选择最短的一条。参数α保证搜索空间得到一定的收缩,而β可以使算法沿着正确的轨迹收敛,避免因为网络结构引起距离的跃变。依据经验并结合实验分析,选取α=3、β=1.5可同时获得较好的效率与精度。

2　实验与分析

2.1数据集

本文使用斯坦福大规模网络数据平台提供的科学合作作者论文网络COND和E-mail网络Letter评测算法有效性。COND包含了浓缩物质物理领域的近21 360篇文献及133 073个引用关系。E-mail网络Letter共收集到4 136个用户及其相互联系形成的27 653条边。由网络的平均度可得,Letter较COND网络稀疏。采用随机网络Random和根据Barabási模型生成的无标度网络Scale-Free作为对比实验网络。实验参数见表1。

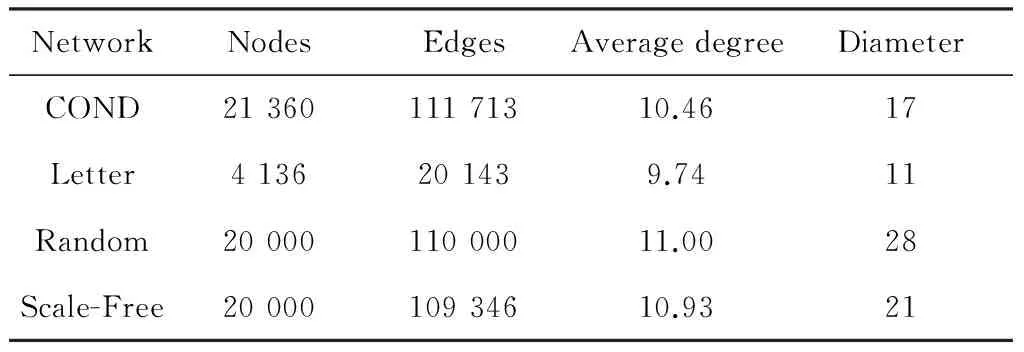
表1　实验网络参数

本文引入LBFS算法[9]、CDZ算法作为对比,从算法精度和算法效率两个方面比较各算法的性能。算法精度用平均路径比P(PathRatio)度量,

(7)

2.2实验与结果分析

CDZ算法选择网络总节点的10%作为中心节点,通过Dijsktra算法计算中心节点之间的最短路径距离; LBFS算法通过最优覆盖策略选择路标,以路标为根节点构建最小生成树将所有节点纳入路标所在的区域,由广度遍历算法计算该区域中任意两点间的最短路径。实验随机取20组源与目标节点对,计算各算法平均路径比,结果如表2所示。

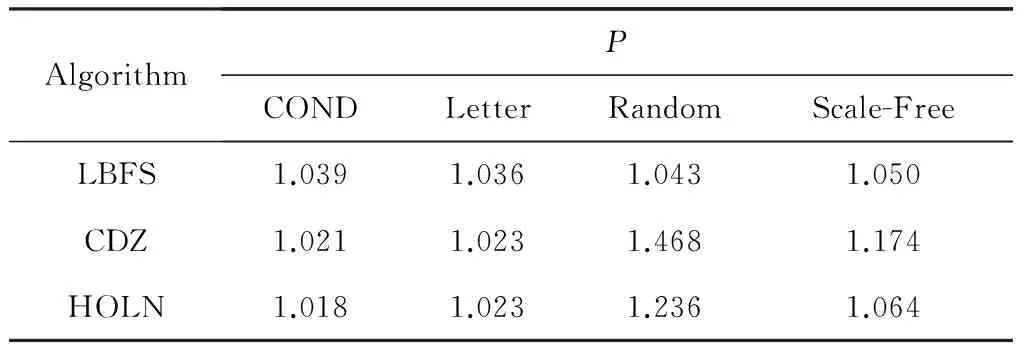
表2　算法在不同网络上的PathRatio值

对于COND网络和Letter网络,CDZ算法和HOLN算法的近似准确性相对于LBFS方法有明显提升,且在密集网络COND中效果更好。这是因为CDZ和HOLN算法利用了实际网络的高聚集性及幂律分布特征进行结构优化,对COND和Letter这类网络能起到很好的效果,而LBSF算法采用的是贪心策略。在无标度网络上,HOLN算法使用了引导策略,一定程度上规避了对中心节点的完全依赖,最终路径比P较CDZ算法好,与LBFS接近。因此,HOLN算法在不完全满足实际网络特性的网络上精度尚可,而在实际社会网络中,其路径发现准确程度非常高。

在运算效率上,实验随机取1 000组源与目标节点对,分别计算在不同规模的无标度网络上的预处理时间Tinit(HOLN算法计算社区间距,CDZ算法取全局中心节点并计算间距,LBSF算法选择路标并将节点纳入路标区域)和算法运行时间Tq,实验结果见图4、图5。

从图4和图5可以看出,HOLN算法具有非常明显的性能优势。LBSF算法在网络规模较小时,预处理时间开销最小,但随着网络规模的增大,达到4 000个节点后,预处理时间开销超过了HOLN算法。而且LBSF在路径计算时间的性能上为三者中最差,随着网络规模的增大而快速增加并且没有明显的收敛趋势。

图4　不同算法的预处理时间Fig.4　Pretreatment computing time of different algorithms

图5　不同算法的路径计算时间Fig.5　Path computation time of different algorithms

CDZ算法预处理时间远大于其余两者,尤其是在网络规模增大后,这是因为CDZ算法直接在原网络中选择中心节点进行距离估算。HOLN算法通过分层策略对原网络进行降解,实现了高效的社区间距计算,提高了整个算法的计算性能。

源节点与目标节点间可能跨越多个社区,跨越社区的数量可能会影响最短路径算法的准确度。以COND网络为例,HOLN算法在跨越不同社区数量时的性能比较如表3所示。表3中短距是指跨越1～3个社区的源与目标对,中距是跨越了4～6个社区,长距则跨越了7个以上的社区。随着跨越社区距离的增加,HOLN算法精确度越来越高,源与目标对的距离越远,第2阶段的中心点距离估算所产生的估计误差越小,当源与目标对的距离很近时,不仅估计的误差会增大,还可能因网络结构不良收缩引起距离的跃变使得精确度降低。

由实验可知,在具有无标度特征的大规模社会网络中进行路径发现,尤其是在密集网络或远距节点对的路径计算,HOLN算法在精度和效率上都有令人满意的表现。

表3　HOLN算法在跨越不同社区数量时的性能比较

3　结束语

面向大规模社会网络中的路径发现问题,本文提出了一种基于重叠节点的分层网络的近似最短路径发现算法,能有效提高路径发现的精度和计算性能。其中重叠节点和分层网络起到了简化网络和减少节点遍历的作用; 而社会网络的高聚集性及幂律分布特征保证了通过中心节点计算社区间距的可行性。HOLN算法是一种高效的最短路径近似算法,随着社会网络的多样化,如何将算法应用到动态更新的网络中将成为下一步研究重点。

[1]唐晋韬,王挺,王戟.适合复杂网络分析的最短路径近似算法[J].软件学报,2011,22(10):2279-2290.

[2]TRETYAKOV K,ARMAS-CERVANTES A,GARCA-BAUELOS L,etal.Fast fully dynamic landmark-based estimation of shortest path distances in very large graphs[C]//Proceedings of the 20th ACM Conference on Information and Knowledge Management.Glasgow,United Kingdom:ACM,2011:1785-1794.

[3]宋青.大规模网络最短路径的分层优化算法研究[D].上海:上海交通大学,2012:21-30.

[4]PALLA G.Uncovering the overlapping community structure of complex networks in nature and society[J].Nature,2005,435(7043):814-818.

[5]LANCICHINETTI A,FORTUNATO S,KERTESZ J.Detecting the overlapping and hierarchical community structure of complex networks[J].New Journal of Physics,2008,625(15):19-44.

[6]NEWMAN M E J.Detecting community structure in networks[J].The European Physical Journal B:Condensed Matter and Complex Systems,2004,38(2):321-330.

[7]OSBOURN G C.The structure of scientific collaboration networks[J].Proceedings of the National Academy of Science,2001,98(2):404-409.

[8]NEWMAN M.Networks:An introduction[J].Astronomische Nachrichten,2010,327(8):741-743.

[9]CORNEIL D G,OLARIU S,STEWART L.The LBFS structure and recognition of interval graphs[J].Siam Journal on Discrete Mathematics,2009,23(4):1905-1953.

Shortest Path Algorithm of Social Network Overlapping Nodes

ZHU Kai-cheng,CHENG Hua

(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

By path analysis,the relationship and connecting characteristic in social networks can be discovered,especially,in criminal networks.In this paper,the community discovery algorithm is utilized to obtain the overlapping nodes and construct the hierarchical network model of real social network.And then,by considering the high clustering coefficient and power law distribution of social network,this paper proposes an overlapping-nodes-based hierarchic path algorithm,HOLN,in which the core node distances are used to stand for community space and the overlapping nodes are searched preferentially to simplify node traversal.By the comparison experiment in the scientific cooperation network,it is shown that HOLN algorithm can attain satisfactory performance on the both accuracy and efficiency.

social network; shortest path; overlapping nodes; hierarchical network

1006-3080(2016)04-0552-05

10.14135/j.cnki.1006-3080.2016.04.017

2015-11-04

朱恺骋(1991-),男,浙江杭州人,硕士生,研究方向为社会网络。

通信联系人：程 华,E-mail:hcheng@ecust.edu.cn

TP301

A