薄镜面力矩校正在自由谐振模式下的定标计算

范磊，乔兵，王富国

（中国科学院长春光学精密机械与物理研究所，长春 130033）

薄镜面力矩校正在自由谐振模式下的定标计算

范磊，乔兵，王富国

（中国科学院长春光学精密机械与物理研究所，长春 130033）

薄镜面面形的主动校正方式主要分为力校正和力矩校正两种。在技术较为成熟的力校正基础上，为丰富和完善主动支撑技术，提出利用自由谐振模式定标法分析薄镜面的力矩校正能力。首先分析了薄镜的力矩校正在自由谐振模式下的波前拟合和水平校正力的定标计算方法。然后，以一块口径400mm薄镜作为分析对象，建立了相应的有限元模型，完成了该反射镜水平校正力的定标计算。最后，针对某一工况镜面变形，求解了相应的校正系数，通过计算，校正后镜面面形残余误差为5.4nm，校正效果明显。结果表明，薄镜面的力矩主动校正是可行的，提出的自由谐振模式定标计算方法也是合理的，为进一步开展力矩主动校正技术的研究提供了一种参考。

自由谐振；主动光学；薄镜面；力矩校正；有限元法

薄镜面主动光学是通过能动地校正镜面变形来实时补偿光学波面误差，以期光学系统达到最佳的成像质量［1］。镜面的主动校正方式一般分为力校正和力矩校正（水平力校正）两种。图1所示为两种镜面主动校正方式示意图。

图1　镜面主动校正方式

由图1可以看出，两种方式都能到达校正镜面面形的目的，只是结构形式上存在差异。设系统波前误差为W，为校正该波前误差，校正力Fa和校正力力矩M都应产生-W的波前，即Fa和M应分别满足：

式中：C为校正力刚度矩阵；D为校正力矩刚度矩阵。

根据图1（b）可知，式（2）中校正力矩M为：

式中：Fh为水平校正力，L力臂。

目前研究和应用较多的是基于力校正的薄镜面主动支撑技术：国外，从ESO最先开展的1m薄镜面主动光学实验到VLT望远镜8m主镜，采用的都是力主动校正方式［3］；国内，南京天文光学技术研究所、成都光电技术研究所、长春光学精密机械与物理研究所和苏州大学现代光学技术研究所都开展了1m口径以下力校正的薄镜面主动光学的研究［6］。

但是，关于力矩校正的研究国内外都相对较少。国外，主要集中于利用压电陶瓷片对新型超薄复合反射镜进行主动校正［7］；国内，长春光学精密机械与物理研究所范磊等通过对水平校正力的优化，对一轻量化反射镜模型面形进行了静态优化分析，效果明显［9］；成都光电技术研究所研究人员对一块集成了力矩促动器的六边形轻量化金属镜进行了分析计算，结果显示能够很好地校正低阶Zernike像差［10］。

为了进一步开展薄镜面的力矩主动校正研究，分析该方式的主动校正性能。本文采用自由谐振模态定标法，对口径400mm薄镜，建立了主动校正模型，完成了水平校正力的定标计算，并对某一工况下的镜面变形进行了校正。

1　自由谐振模式定标原理

1.1自由谐振模式下的波前拟合

波前拟合和校正力求解构成了主动光学的两大关键技术。其中，波前拟合一般采用两种方式：一是准Zernike多项式拟合，二是自由谐振多项式拟合［1］。自由谐振模式可以用来拟合镜面面形是由于它与准Zernike多项式接近且各模态振型相互正交。图2和图3所示分别为圆域Zernike多项式和自由谐振模式振型图。

图2　Zernike多项式

两者的区别在于Zernike多项式拟合侧重于光学像质的表达，单位圆内方差为1，与薄镜面结构的变形特性无关；自由谐振多项式拟合侧重于机械结构特性的表达，容易建立拟合面形和校正力的求解关系，但其局限性在于模态振型函数与薄镜物理几何参数相关，不具有统一的表达形式，一般需利用有限元法求解。

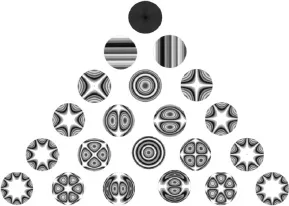
图3　自由谐振模态振型

在薄镜面上选取m个节点，要求满足m＞n。利用有限元方法计算每个节点对应的n项模态振型向量值，组成模态振型矩阵：

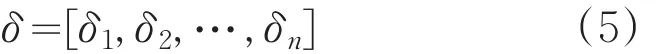
通过有限元分析求取镜面变形节点位移值w=（w1，w2，…wm）T，则建立拟合方程如下：

设薄镜波前面形误差为w，取前n阶自由谐振振型向量δi（i=1，2，…，n），拟合系数为ai，则利用自由谐振多项式拟合有：

利用最小二乘法求解拟合系数为：

1.2水平校正力的模式定标计算

不同的波前拟合方式对应不同的校正力求解法，其中准Zernike多项式拟合对应的是阻尼最小二乘法；自由谐振模式拟合对应的是模式定标法。模式定标法的基本原则就是对于任意一阶模态振型，施加定标后的校正力能够使镜面恢复该阶模态振型，且振型对应的面形误差都为预先设定的某归一化值（如633nm，1000nm等）。

模式定标法主要利用有限元方法求解，参考文献［2］提出基于校正力模型的模式定标计算方法，本文给出了一种针对校正力矩的模式定标计算方法，计算流程如图4所示。

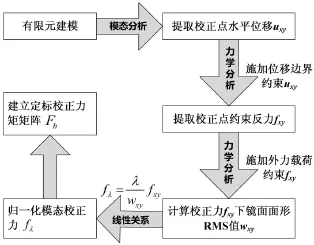
图4　水平校正力定标流程

如图4所示，设校正力矩由薄镜背部离散分布的k个水平校正力完成，则对于第i阶谐振模态振型，相应地导出这k个节点对应的水平位移uxy，将uxy作为边界约束条件重新施加到这k个节点，通过有限元静力学分析计算，求取这k个节点的约束反力 fxy和对应的镜面面形wxy，根据力与位移的线性关系，当镜面面形归一化为λ时（λ=633nm，或其它设定值），根据作用力与镜面变形的线性关系，可计算第i阶模态振型归一化后的水平校正力 fλi为：

则对于实际薄镜的镜面变形，根据前n阶自由谐振模式波前拟合结果，利用标定后的水平校正力计算实际水平校正力 f为：

2　Φ400mm反射镜力矩校正模式定标

为了进一步验证上述理论分析，本文选用一块Φ400mm平面反射镜作为分析对象。其中，反射镜厚度为8mm，径厚比为50。

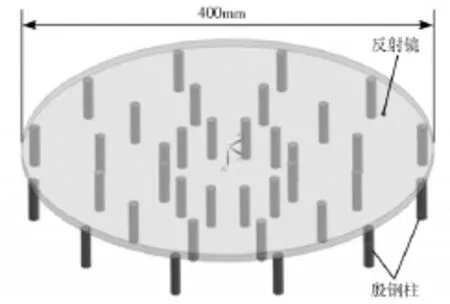
图5　反射镜结构模型

为施加水平校正力，在反射镜背面粘接36个殷钢柱，每个殷钢柱高度为42mm。如图5所示为该反射镜结构模型，36个殷钢柱分布在反射镜背部的3个支撑圈上，支撑圈半径分别为r1=65mm，r2= 130mm，r3=195mm。

2.1反射镜的主动校正建模及模态分析

反射镜材料选用微晶玻璃，殷钢柱选用与其线胀系数相匹配的殷钢材料，相关物理参数如表1所示。

表1　物理参数表

在有限元分析软件MSC.PATRAN中建立有限元模型如图6所示，借用有限元分析软件MSC. NASTRAN分析该模型的前10阶自由弯曲模态振型（除去刚体模态振型），其振型图如图7所示。

图6　反射镜有限元模型

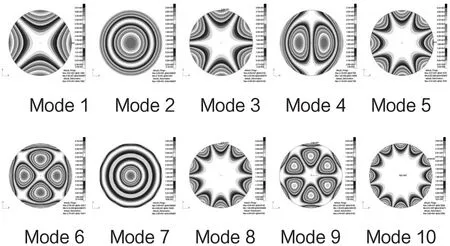
图7　反射镜前10阶模态振型

2.2水平校正力标定计算

依据图3的定标计算流程，首先提取上述10阶模态振型中36个殷钢柱自由端在各阶自由弯曲模态振型下的水平位移Ux和Uy，并将其重新施加到各点，计算薄镜变形，然后从结果文件中提取36点的约束反力Fx和Fy，并计算相应的镜面面形Wxy。根据公式8计算出标定后镜面面形误差统一为λ时的水平标定力，该过程的相关标定计算结果如表2所示，前10阶标定校正后镜面面形云图如图8所示。

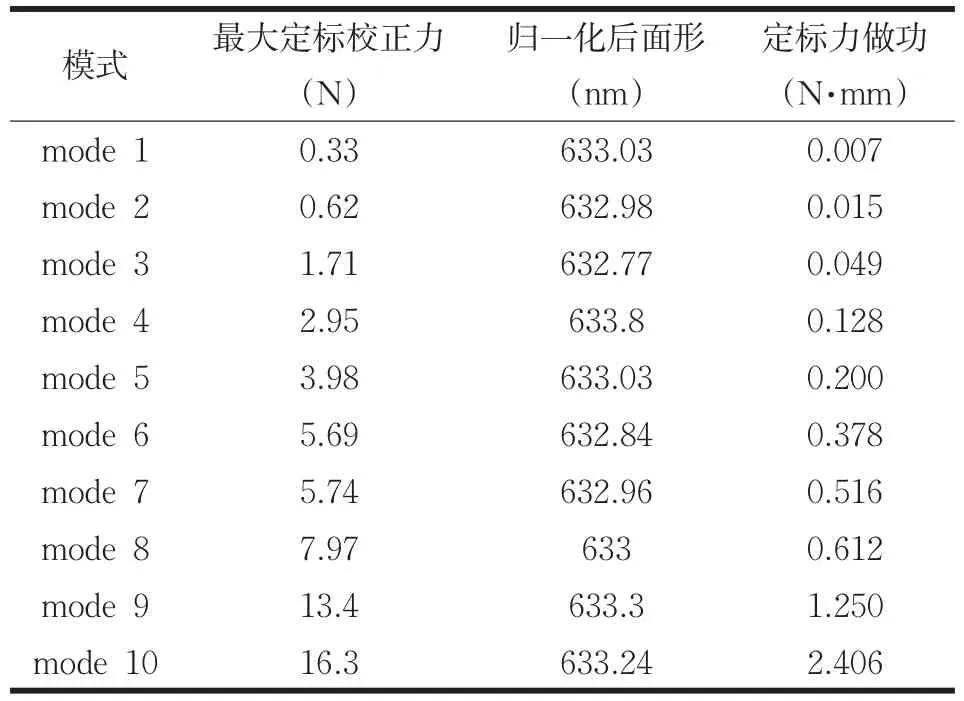
表2　水平标定力计算结果

图8　校正后前10阶镜面面形云图

由图8可以看出，标定后的镜面变形云图同自由谐振振型很相似；从水平标定力的最大值可以看出，随着校正阶数的增加，最大校正力增大，且所有校正力所做的功符合阶数越大做功越多的原理。

2.3镜面变形校正计算模拟

设该薄镜在指向天顶状态下，由背部均布的3点支撑，其中支撑半径为130mm，计算重力作用下的变形，变形云图如图9所示，除去刚体位移后的镜面变形RMS值为545.8nm。

图9　3点支撑下反射镜变形云图

根据公式（7）计算自由谐振模式下的波前拟合系数和校正系数如表3所示。

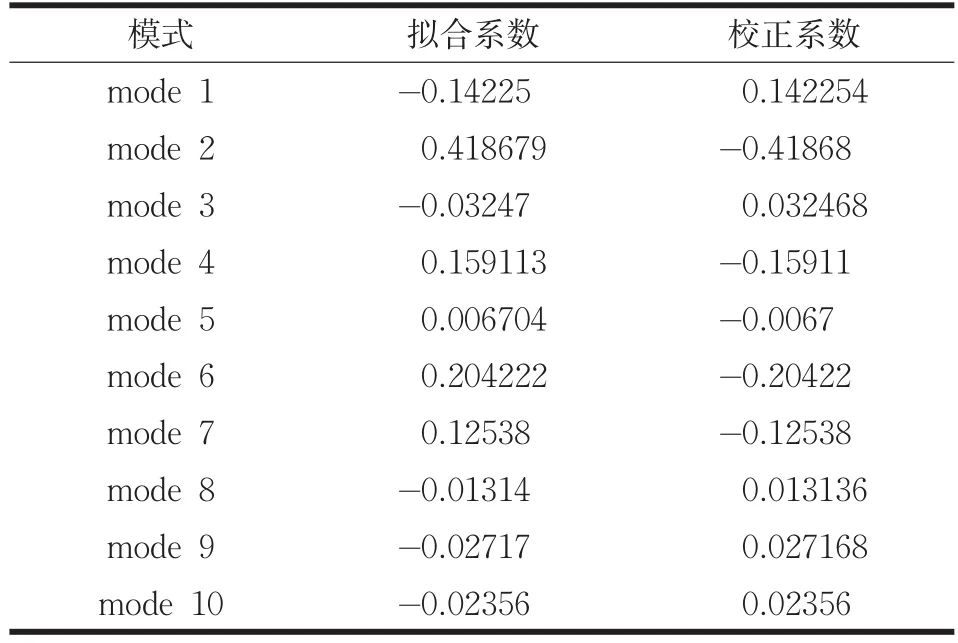
表3　波前拟合系数和校正系数

利用上述计算的校正系数，根据公式（9）计算出各点水平校正力的大小，施加到反射镜模型上，计算镜面校正变形，模型施加载荷如图10所示，反射镜变形云图如图11所示。计算结果显示，除去刚体位移后的镜面校正变形RMS值为551.2nm。计算可得校正残余误差为5.4nm，约为0.0085λ（λ= 633nm）。结果显示校正效果比较理想。

图10　水平校正力载荷分布图

图11　校正力作用下镜面变形云图

3　结论

本文基于自由谐振模式定标原理，提出了一种针对薄镜面力矩校正模型的模式定标计算方法。以400mm薄镜作为分析对象，利用上述定标法完成了该薄镜水平校正力的定标计算，并针对某一工况下薄镜的变形，进行了相应地校正，结果显示，校正后镜面面形的残余误差约为5.4nm，校正效果比较明显。上述结果表明采用力矩校正方式来完成薄镜面的主动校正是可行的，在目前较为成熟的力校正的基础上，进一步完善了薄镜面主动支撑技术，对薄镜面的支撑技术具有一定的参考价值。

［1］苏定强，崔向群.主动光学—新一代大望远镜的关键技术［J］.天文学进展，1999，17（1）：1-14.

［2］崔向群.采用主动光学的大口径单块薄镜面的支撑系统［D］.南京：中国科学院南京天文仪器研制中心，1995.

［3］陈夫林.620mm薄镜面主动支撑技术研究［D］.北京：中国科学院，2012.

［4］张玉方，李国平.用于薄镜面主动光学的音圈力促动器设计［J］.光学·精密工程，2013，21（11）：2836-2843.

［5］李宏壮，张景旭，张振铎，等.620mm薄镜面主动光学望远镜校正实验［J］.红外与激光工程，2014，43（1）：166-172.

［6］倪颖，黄启泰，余景池.超轻超薄反射镜主动支撑方案优化设计［J］.光电工程，2008，35（9）：22-26.

［7］Liu Celia H.Structural analysis and design of adaptive lightweight mirrors［D］.USA：Massachusetts Institute of Technology，1993.

［8］Johannes K D，Robert Honkel，Mathias V A，et al. Development and manufacture of an adaptive lightweight mirror for space application［J］.Smart Materials and Structures，2003，12：1005-1016.

［9］范磊，王志，曹玉岩.基于力矩主动校正的反射镜支撑分析［J］.红外与激光工程，2015，44（4）：1273-1277.

［10］Lu Weixin，Zhou Hong，Fan Xinlong，et al.Test of aPrototypeofLightweight，ActiveMirrors［C］. SPIE，2014，9280：U1-U6.

［11］王志.碳纤维复合材料的智能复合反射镜技术研究［J］.长春理工大学学报：自然科学版，2013，36（6）：6-9.

［12］吴小霞.4m SiC主镜的轻量化及支撑技术［J］.长春理工大学学报：自然科学版，2013，36（6）：11-14.

［13］石广丰，刘丽萍，袁帅.薄膜加载变形的有限元数值优化反演求解［J］.长春理工大学学报：自然科学版，2011，34（1）：61-70.

Calibration of Moment Correction for Thin Mirror Surface Based on Free Harmonic Vibration Modal

FAN Lei，QIAO Bing，WANG Fuguo
（Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033）

Active correction means for thin mirror surface could be divided into force correction and moment correction. In order to enrich and improve the active support technology in active optics，calibration in free harmonic vibration modal was provided to evaluate the capacity of moment correction for thin mirror.First，the methods of wave front fitting and horizontal corrective force solving for moment correction model in the free harmonic vibration modal were provided.Then，as an analysis object，FE model of a thin mirror with the aperture of 400mm was built and the horizontal corrective forces were calibrated in detail.Last，the coefficients of corrective forces were solved in a load case，and the residual error of surface was 5.4nm after corrected.In conclusion，such active moment correction for thin mirror was effective，and the calibration in free harmonic vibration modal was reasonable.So the study provided an important value to moment correction for mirror surface.

free harmonic vibration modal；active optics；thin mirror；moment correction；FEM

TH761

A

1672-9870（2016）03-0009-05

2016-02-11

范磊（1986-），男，博士，助理研究员，E-mail：fanlei1995@sina.com