姿态参数模拟解算电路的校正设计与测试*

于津丰，程为彬，蔡　贝（西安石油大学电子工程学院，西安710065）

姿态参数模拟解算电路的校正设计与测试*

于津丰，程为彬*，蔡贝
（西安石油大学电子工程学院，西安710065）

分析了传统姿态参数模拟解算过程中大角度无法解算的原因，提出传统姿态参数模拟解算过程中饱和失真、非线性失真的解决方法，并设计了校正电路。通过校正系数电路解决饱和失真的问题，采用折线拟合电路提高解算精度。利用离散方法对所设计的电路进行测试，能够明显的发现误差角度减小，最大误差角度减小为0.417°，90°时误差角度减小为0.3°。实验结果表明，输出角度曲线的非线性得到明显改善，验证了校正系数调节电路设计的可行性。

模拟解算；校正电路；折线拟合；反正弦函数

采用反函数电路对三轴加速度计的输出进行模拟解算，可以稳定、快速、有效地解算出倾斜角和工具面角［1］，这对确定井下钻井工具姿态参数、控制井眼轨迹起着重要的作用［2］。传统的姿态参数求解方法包括数字求解和模拟求解2种方法，数字方法可利用不同的算法对姿态参数进行解算［3-4］，但是对 A/D的位数要求很高并且A/D转换、采样/保持等过程容易引入各种误差。模拟解算以井眼轨迹测量的基本原理作为依据，主要有2种方法，第1种是把反三角函数用级数展开，再利用乘法电路和加法电路叠加实现［5］，在实际应用中有函数展开存在误差且电路运算量太大等问题；第2种是采用模拟函数发生器，利用反正弦电路对姿态参数进行直接解算［6］。在反正弦解算实验过程中发现，解算值在大角度（85°～90°）时存在严重失真，在85°之后无法解算出正确的角度值。

为解决饱和失真，提高解算精度，本文设计了校正电路，通过对振幅控制电压的调节，使输出角度的饱和失真得以改善，并利用折线拟合电路提高解算精度。

1　反函数模拟解算电路校正原理

通过对模拟函数发生器AD639的分析可以发现其采用线性段近似、代数逼近法和基于双极性差分对管电路的近似方法，通过叠加合成连续函数［7］，其芯片内部电路在85°就趋近于饱和，因此解算角度在大角度时存在饱和现象，出现了大角度时的非线性失真问题。

结合AD639内部原理框图的分析，发现可以利用AD639内部电路除法部分，在不影响实际输入的前提下，改变外加振幅控制电压，可以实现对模拟解算输出值的校正。再通过折线拟合电路最终实现倾斜角的精确解算。

图1为校正电路总体原理框图。

图1　校正电路原理框图

2　反函数模拟解算电路校正设计

2.1校正电路原理

根据模拟函数发生器AD639内部原理框图，可知其最基本的功能函数为［8］

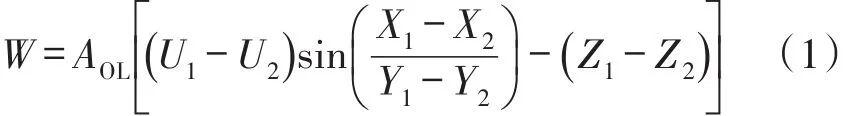
式中：AOL为输出放大器的开环增益（一般为85 dB）；U1、U2为振幅控制电压；X1、X2、Y1、Y2为差动角度输入，角度值与电压值之间的标度因数为50°/V（20mV/°）。

要实现AD639反函数模拟解算，必须断开输出放大器反馈回路，则可以得到：

令Z1=0、U2=0，通过恒等变换式（2）变为：

U1由引脚可编程的精密基准电压源AD584直接提供［9］，由于精度问题 AD584提供的电压为10.011 V。实验中输入端Z2=10.011 sin VX，即Z2是幅值与理论正弦值的乘积。分析后发现，由于输入端为三轴加速度计的模拟输出信号，故输入电压的幅值保持不变。通过调节幅值电压U1，可得，由此获得的新的电压比称为校正系数α。则（3）式可变为：代入，（4）式变为：

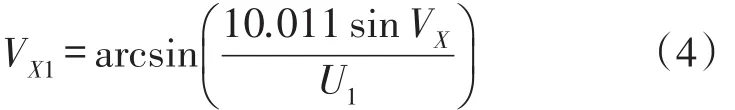
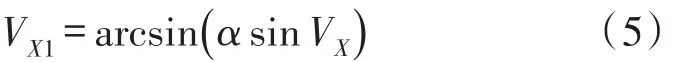
引入校正系数α之后，可以对反函数模拟解算过程引入的失真、误差等进行校正，以达到解决输出角度饱和失真的目的。

为进一步提高输出角度的精度，分析发现输出曲线的特性与下凸曲线［10］类似，并且不失真的部分线性度较好，根据输出曲线的特性将其进行分段，每个区间段内的曲线用一段直线近似代替，设置折点电压，利用二极管正向导通、反向截止的特性，通过外加偏置电压与输入电压之间的压降，控制二极管的关断与导通，实现折线校正电路对失真数据的二次校正，以达到提高精度的目的。

2.2校正电路设计

校正电路的设计主要分为2个部分。

第1部分电路通过校正系数调节电路解决饱和失真的问题。具体的调节电路中以AD584为主设计精密基准电压源作为稳定的振幅电压，再通过以TL084为主搭建的放大电路将AD584的输出端与AD639振幅控制电压的输入端相连，通过改变振幅控制电压的大小，使输出值得到校正。

其具体电路如图2所示。

图2　校正系数调节电路

第2部分为折线拟合电路，校正系数电路解决了饱和失真的问题，但仍存在较大的误差，因此采用折线拟合电路对误差较大的部分进行校正。A1为1∶1的反相器，输出值加在带有偏置电压的二极管上，预先设置偏置电压，当输入电压小于折点电压，二极管关断，此时折线斜率通过可调电阻W1进行调节。当输入电压大于折点电压VF时，二极管导通，此时折线斜率由可调电阻W2进行调节。

其具体电路如图3所示。

图3　折线拟合电路

在实际的测量过程中发现，采用普通二极管会对电路产生较大的非线性影响，具体表现在折点附近输出值的失真以及校正后曲线趋于二次函数。改进后采用超高速开关二极管，利用其正向快速导通，反向快速截止的特性，减小了其对电路的非线性影响，并辅以外围电路减小放大器的误差和扰动，使输出值的精度得到提高。

3　实验测试与分析

3.1校正电路离散测试数据

本文采用离散测试的方法，主要测试了电路的精度，通过各组数据之间的对比，可以清晰地看出校正后电路误差值的减小。

与传统模拟解算过程中，对输入数据直接进行解算相比。实验数据测量过程中，以60°为例，对电路进行必要的预热之后，输入60°所对应的输入电压，通过对幅值电压U1的调节，使模拟解算电路的实际输出电压与理论输出电压基本一致，之后保持U1值不变，以15°作为步进间隔逐次输入0°～90°的输入电压，并进行采样。根据三轴加速度计在45°附近线性最优的特性，实验过程中分别以30°，45°，60°和90°作为参考进行校正，寻找最佳校正系数，测量后得到部分输出采样数据如表1所示。

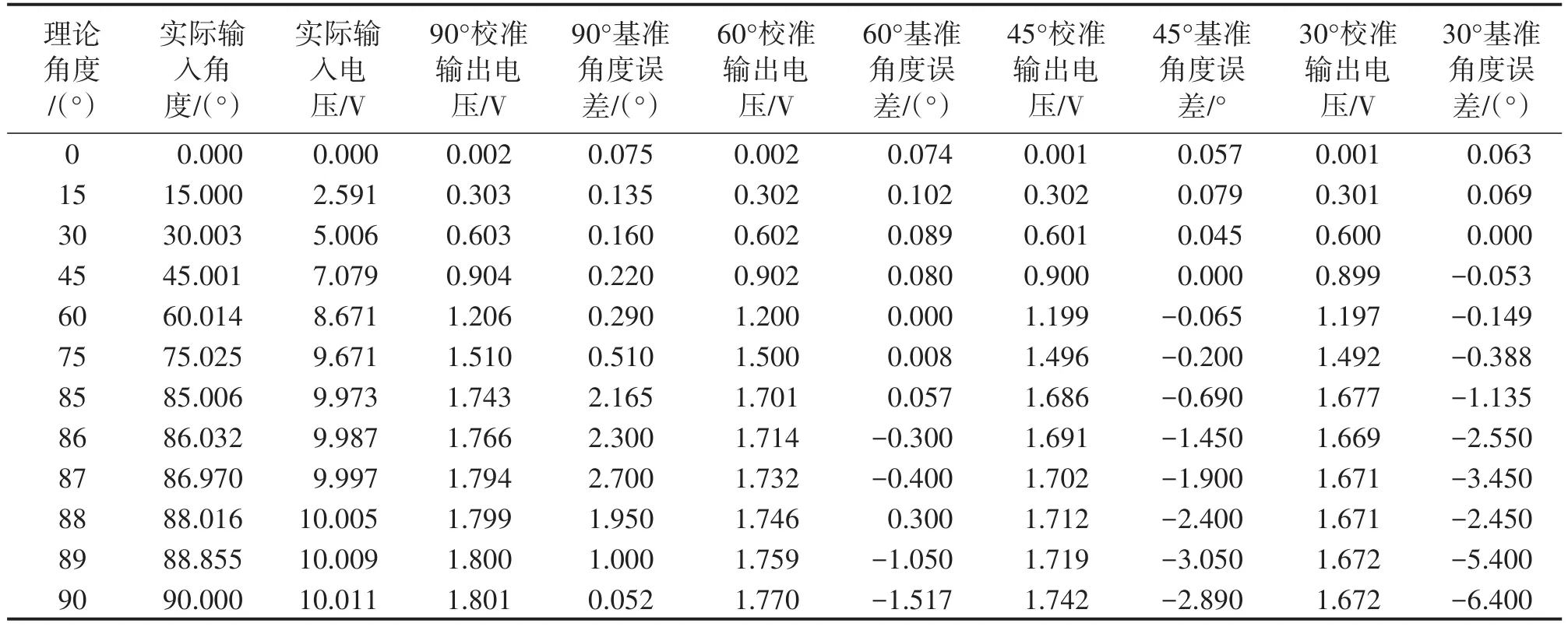
表1　校正系数调节电路测试数据

校正系数电路解决了AD639反正弦电路在大角度时的饱和问题，但是大角度时输出角度仍有失真，为了解决失真问题，采用折线拟合电路，设置85°对应电压1.7 V为折点电压，通过调节W1使其阻值与R0相等，即第1部分曲线输出值不变，当输入电压高于1.7 V之后，调节电阻W2对非线性部分进行拟合。其折线拟合电路测试数据如表2所示。

表2　折线拟合电路测试数据

姿态参数模拟解算电路及其校正电路实物如图4所示。

图4　校正电路实物图

3.2数据分析

电路实验中，将理论输入角度对应下的输入电压保留到小数点后第3位作为电路的实际输入。在对实验数据进行处理时，以实际输出角度为基准进行分析，实验数据及误差曲线如图5所示。

在图5（a）中可以看出，各参考角度的输出曲线在0°至85°的范围内，失真较低，线性度较好，非线性失真主要集中在85°到90°的大角度范围，故85°以前输入值以15°作为步进间隔，85°之后以1°作为步进间隔，重点分析大角度时的失真校正。

图5（b）是大角度非线性失真曲线，90°为基准与传统的直接解算相同，校正系数α=1，在数据中作为与其他校正系数的对比，可以明显发现在85°之后解算角度趋于饱和，无法解算出实际角度值。30°为基准时，最大角度误差为-3.71°，校正系数α=0.9959，失真状况与传统算法相比更加严重。45°为基准时，最大角度误差为-2.89°，校正系数α=0.9966，失真状况与传统算法相比更加严重，但是通过大角度数据分析发现，饱和点明显增大，有一定校正效果。60°为基准时，最大角度误差为-1.517°，校正系数α=0.997 6，失真状况与传统算法相比有了明显的改善，除了89°和90°之外，其余角度的误差值均小于0.5°。由此可得，60°为基准调节校正系数时，与其他基准角度相比输出曲线的线性度更好。

图5（c）是拟合前后输出角度对比，85°为折点角度，60°为基准作为输入角度，调节时发现折线具有二阶曲线的特性，若90°误差减小，则86°误差增大，反之亦然。通过调节，最大误差角度为-0.417°，90°时误差角度为0.3°，此校正数据与理论输出角度接近，最大误差角度的相对误差为0.463%。

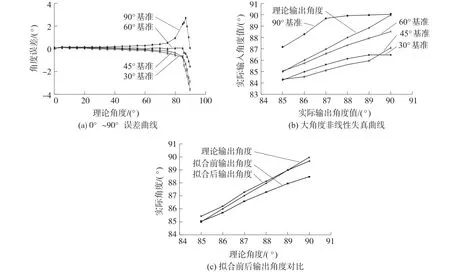
图5　测量数据误差曲线

4　结论

本文通过校正系数调节电路解决了大角度饱和失真的问题，同时利用折线拟合电路对输出角度的非线性失真进行校正。采用离散测试的方法对电路进行了验证，通过对数据的分析和比较发现，电路输出曲线的饱和失真情况得以解决，非线性失真问题得到明显改善，精确度大幅提高。实验结果表明校正设计方案可行，电路结构简单，实时性良好，可以实现模拟解算电路大角度非线性失真的校正。

［1］ 王晓翠，程为彬，李彬，等.姿态参数的模拟解算电路设计与分析［J］.传感器与微系统，2014，33（4）：72-79.

［2］ 葛亮，胡泽，陈平.井下工程参数随钻测试系统设计［J］.传感器与微系统，2013，32（8）：105-107.

［3］ 程为彬，潘萌，汤楠，等.基于预置欧拉旋转的垂直姿态测量［J］.仪器仪表学报，2014，35（8）：1817-1822.

［4］ 杨全进，蒋海旭，左信.一种用于井下钻具旋转中动态方位测量的新方法［J］.石油钻采工艺，2014，36（1）：40-43.

［5］ 陈琳，程为彬，郭颖娜，等.基于井下姿态测量的余弦函数模拟求解电路设计［J］.电子器件，2009，32（1）：104-107.

［6］ 王晓翠.旋转导向钻井工具姿态参数的模拟计算［D］.西安：西安石油大学，2014.

［7］ Barrie Gilbert.A Monolithic Microsystem for Analog Synthesis of Trigonometric Functions and Their Inverse［J］.IEEE Journal of Solid-State Circuits，1982，17：1179-1191.

［8］ AD639Datasheet［DB/OL］.www.analog.com，1999.

［9］ AD584 Datasheet［DB/OL］.www.analog.com，1999.

［10］王彩军，黄智进，吴兴惠.传感器线性化电路［J］.杭州电子科技大学学报，1997，16（5）：48-51

程为彬（1970-），男，西安石油大学电子工程学院教授，主要研究方向为石油仪器及其智能化、检测技术与自动化装置、非线性电路理论及其应用等领域的教学和科研工作，wbcheng@xsyu.edu.cn；

于津丰（1989-），男，天津人，西安石油大学硕士生，主要研究方向为检测技术与自动化装置，abneryjf@126.com。

Correction Design and Test of Attitude Parameters' Analog Computation Circuit*

YU Jinfeng，CHENGWeibin*，CAIBei
（School of Electronic Engineering，Xi'an Shiyou Uniυersity，Xi'an 710065，China）

The reason why the large angles cannotbe computed is analyzed in the process of traditional attitude parameters'analog computation，and a calibrationmethod is put forward to resolve the saturation distortion and nonlinear distortion in the traditional attitude parameters'analog computation experiment，and the correcting circuit is designed.The saturation distortion problem is resolved by correction coefficient circuit，and the partof error is corrected by piecewise approximation circuit.The designed circuit is tested by discretemethod，the error of angles is reduced clearly，themaximum error of angles is 0.417°，and the error of angles in 90°is 0.3°.The experimental result shows that nonlinearity of the angle output curve is improved obviously.The feasibility of the correction coefficient regulating circuit is verified.

analog computation；correction circuit；piecewise approximation；arcsine function

TE243；TP274.2

A

1005-9490（2016）04-0946-05

项目来源：国家自然科学基金项目（61174191）；陕西省科学技术研究发展计划项目（2011K06-27）；陕西省教育厅产业化培育项目（2013JC08）

2015-09-09修改日期：2015-10-21

EEACC:128510.3969/j.issn.1005-9490.2016.04.037