基于纵/侧向运动解耦的双足机器人侧向步态轨迹规划

南京工程学院　何　昕

基于纵/侧向运动解耦的双足机器人侧向步态轨迹规划

南京工程学院何昕

双足机器人的运动方式类似于人类，依靠两腿交替接触地面，获得支撑，完成行走。因此，其对地面状况的适应能力优于轮式或其他移动机器人。但是，其行走步态轨迹的规划也较这些机器人复杂很多。针对双足机器人复杂的多连杆机构，研究了其运动学模型，依据双足机器人行走稳定性条件，对其纵/侧向运动进行解耦。对机器人重心的侧向运动步态轨迹按正弦规律进行了规划，使其满足行走稳定性条件。为双足机器人的步态轨迹工程化规划提供了理论依据。

双足机器人；运动学模型；侧向轨迹规划；解耦

0　引言

机器人是一门综合学科，融合了机械、电子、材料、计算机、传感器、控制技术以及人工智能等多学科的知识。随着“中国制造2025”工业发展浪潮的来临，作为装备制造业的高端产品和大众服务业热门技术，机器人越来越受到普瑞人群的广泛关注。双足机器人是机器人家族中外形最接近人类的一支，它可以像人一样依靠两腿交替行走，因此其对路面环境的适应能力超出了以速度见长的轮式机器人等移动机器人，能适应台阶、斜坡及不平整地面等复杂地面情况。因此，它可以在一定程度上代替人类在有毒、粉尘、噪音、阴暗的环境下进行作业，降低了人类的劳动强度和作业危险性。

日本双足机器人之父加藤一郎说过，机器人应当具有的重大功能之一就是行走功能。双足机器人恰恰是模仿人类行走机理进行双足行进的机器人。双足机器人之所以具有很强的路面环境适应能力，这与其行走机构是分不开的。它与人类有着相近的髋、膝、踝和足底结构，用舵机驱动各个关节转动，从而驱动两腿交替行走。由于双足机器人是典型的多连杆机构，在控制领域属于高阶、非线性和非完整约束系统，纵向与侧向动力学和运动学耦合在一起，因此其轨迹理论设计十分复杂。所以，需要一种能够解耦纵/侧向运动，使步态轨迹规划简单易操作的工程化方法。

1　双足机器人的运动学建模

双足机器人的运动学建模是双足机器人步态轨迹规划的基础，所以在对双足机器人进行步态轨迹规划前，须先对其进行运动学建模。运动学分析是双足机器人运动学建模的基础工作，在使用运动学方程对机器人进行运动学建模前须分析其各个关节（自由度）的相互运动学关系。

解决多关节机器人运动学问题的方法中，较为直观的就属坐标变化法和Denavit-Hartenberg规则，选用这种方法来分析双足机器人的运动学关系。首先建立双足机器人的运动学坐标系，并根据各关节相互运动关系建立运动学方程（即运动学建模）。

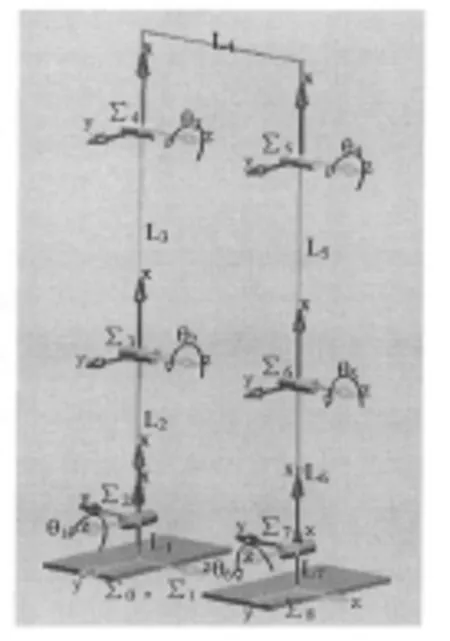
图1　双足机器人的运动学坐标系

图1是双足机器人的运动学坐标系，这里以最为常见的6自由度双足机器人为例。其中6个自由度都是转动自由度。建立的坐标系满足Denavit-Hartenberg规则。

图1中的Lj（j=1，2，3，...，7）表示第j个杆件的长度值，θi表示第i个关节的角度。表1为图1中各个坐标系的信息。

双足机器人的运动学方程的建立：

（1）变换矩阵

变换矩阵描述了机器人相邻自由度之间的运动学关系，是解决各个关节几何关系数学描述的有效手段。运用这样一个数学工具，可以方便地解算出机器人每个末端位姿所对应的各个杆件质心的位姿。

表1　双足机器人运动学坐标系信息

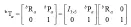
坐标系Σa到坐标系Σb的变换矩阵bTa表示为：

平动变换和转动变换是由trans（bPa）和rotate（k，θ）表示，即：

这里，R（k，θ）是旋转算子，表示坐标系绕k轴旋转θ角后，新坐标系的方位矩阵。

（2）建立运动学方程

根据双足机器人运动学坐标系以及相邻坐标系的变换矩阵iTi+1，那么有：

机器人行走过程中，要求摆动腿足底板始终与地面平行，因此行走过程中有θ1=θ6。所以，根据这一条件可以对变换矩阵进行简化，用θ1取代θ6即可。

根据人类行走特点以及双足机器人的具体参数，将机器人行走速度规划为40mm，步长为80mm，抬脚高度最大值为12mm。

2　纵向/侧向运动之间的耦合

双足机器人步行过程中的侧向运动和纵向运动如图2和图3所示：

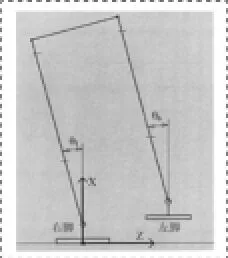
图2　双足机器人侧向运动示意图

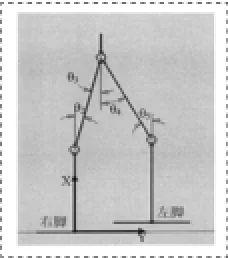
图3　双足机器人纵向运动示意图

从图2和图3易见，机器人的行走过程中，其侧向自由度（θ1、θ6）和纵向自由度（θ2、θ3、θ4、θ5）是协同工作的，机器人的运动纵向运动和侧向运动是一体化的，即纵/侧向运动耦合在一起。这种纵/侧向运动的耦合是仿效人类行走机理的，使其在行走过程中保持稳定。其耦合机理是纵/侧向动力学间的耦合。

3　行走稳定性条件及纵/侧向运动解耦

双足机器人行走必须满足稳定性要求，这一点与轮式机器人有着显著的不同。轮式机器人一般都自然具备稳定性。但是对于双足机器人而言，保持机体的稳定就困难很多。

根据ZMP理论，双足机器人静止时，要想保持稳定性，须满足重心在地面上的投影落在支撑脚与地面的接触平面内。在机器人行走过程中，重心在地面上的投影须在两脚底板（保持与地面平行）地面投影区域之间。如果在该区域之外，双足机器人就有倾倒的趋势。

因此，规划双足机器人的步态轨迹时须时时满足这一稳定性条件。为了使机器人的稳定性更好，一般将重心地面投影保持在机器人两脚底板纵向中心线之间。

了解到双足机器人行走稳定性条件，就可以合理规划重心在地面投影的轨迹即侧向轨迹，使其始终满足稳定性条件。在此基础上规划纵向轨迹，就可以实现双足机器人纵/侧向运动的解耦。

由此可见，如何合理规划双足机器人的侧向步态轨迹成为了其步态轨迹规划的关键一步。

4　侧向步态轨迹规划

在侧向步态轨迹规划中，假设机器人纵向关节静止，只须通过侧向关节的运动驱使机器人重心在两脚与地面接触区域中心线内左右摆动即可。关键在于重心在这两条中心线之间按照怎样规律的曲线进行左右摆动。

从行走平稳角度，重心在侧向平面内变化率不宜过大，否则会导致动态稳定性下降即引起冲击。这一点在重心临近足底中心线时尤为突出。所以，设计的重心侧向移动曲线在整个区间内光滑，在靠近足底中心线时渐小，在离开时渐大，在中间位置最大。这样，既便于重心转换移动方向时减小冲击，又利于转换后快速行进，提高步行的速度。

综上所述，采用了正弦规律的重心侧向移动曲线，下面进行具体侧向步态轨迹规划。

如前所述，在机器人行进过程中，有θ1=θ6=θ。由重心计算公式来计算机器人重心坐标：

其中的Zi是θ的函数，所以机器人重心坐标Zcg也是θ的函数。

双足机器人步行过程可以认为由以下三个阶段组成：起步阶段、双足交替行走阶段和止步阶段。下面分别对此三个阶段进行重心轨迹规划。假设机器人从静止开始，完成三步行走周期，然后停止，设起步周期、单步行走周期和止步周期都是2s。

将机器人重心坐标代入以上三个表达式中，得到以下关系：

借助Matlab计算，绘出θ随时间t的函数曲线，如图4所示。

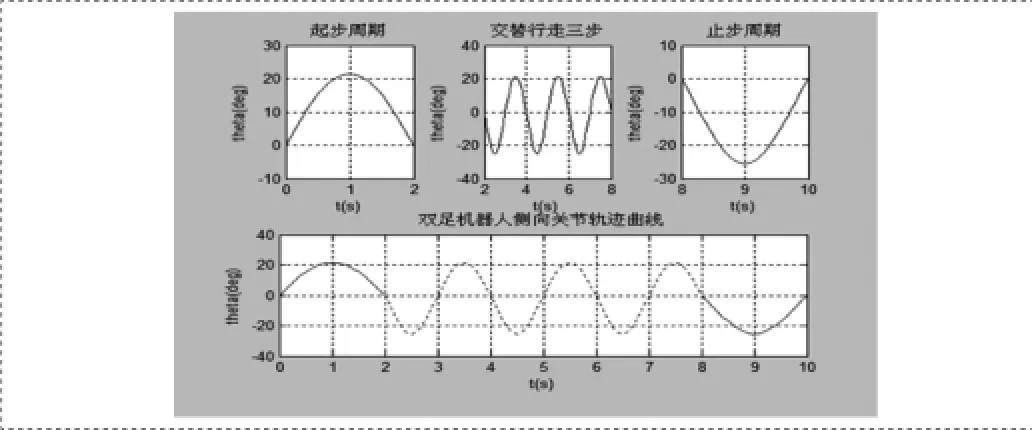
图4　双足机器人侧向自由度轨迹曲线

由于在建模时将机器人的运动学进行人为简化，即认为纵向和侧向之间是没有耦合，加之机器人零件、配件的加工与装配过程中有加工及装配误差，必然导致其采用的运动学模型与理论实际运动学模型间存在一定的偏差。因此，上文中所设计的关节轨迹直接用于舵机运动，还无法完全实现步态轨迹的平滑，须在机器人在线调试阶段进行在线校正。

5　结论

通过建立双足机器人运动学坐标系，依据6自由度多连杆之间的连接关系以及杆件参数，建立6自由度双足机器人的运动学模型，并依据稳定性条件将纵向/侧向运动解耦。依据正弦曲线对侧向步态轨迹进行规划，得到了各个侧向关节转动角度轨迹。为纵向轨迹规划打下了基础，也为双足机器人的步态轨迹的工程化规划提供了理论依据。