网状多端高压直流输电系统负荷分配优化控制

冷欣,宋文龙，刘一琦，王睿, 王立辉

(1.东北林业大学 机电工程学院，黑龙江 哈尔滨 150040； 2.哈尔滨移动公司 无线优化室，黑龙江 哈尔滨 150001; 3.东南大学仪器科学与工程学院，江苏 南京 210096)



网状多端高压直流输电系统负荷分配优化控制

冷欣1,宋文龙1，刘一琦1，王睿2, 王立辉3

(1.东北林业大学 机电工程学院，黑龙江 哈尔滨 150040； 2.哈尔滨移动公司 无线优化室，黑龙江 哈尔滨 150001; 3.东南大学仪器科学与工程学院，江苏 南京 210096)

为了确保高压直流输电系统中线路损耗达到最小，针对网状多端高压直流输电系统，提出了一种基于改进型下垂控制的负荷分配优化方法。该方法通过引入目标变换器相邻两台变换器的电压和电流信号，取其平均值为补偿分量投入到传统的下垂控制中，同时利用低带宽通信网络，实现直流母线电压的提升并实现了负荷功率在线路阻抗不同的情况下的最优分配。利用上述控制方法对线路阻抗的不同取值和通信延迟情况下的适用性进行了详细的分析。仿真结果表明：网状多端高压直流输电系统在不同情况下的最优化负荷分配，实现了系统的优化稳定运行。所提出的方法确保了直流输出偏差的最大值保持在额定电压参考值的5%以内，保证了网状多端高压直流输电系统的线路损耗最小化，提高了能源利用效率。

多端高压直流输电；负荷分配；网状结构；下垂控制；低带宽通信；线路损耗最小化; 优化控制

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160711.0834.002.html

随着直流输电系统的日益发展，多端高压直流输电(MT-HVDC)技术获得了越来越多的关注[1-4]。与传统的交流电网相比，直流输电网具有线路造价 低，有功损耗小，适宜于海下输电和抑制系统的短路电流等优势[5-6]。由于近年来能源和环境问题面临的挑战，大力发展包括太阳能、风能等可再生新能源是抑制高耗能行业过快增长的必然选择。一般近海风电场由多个输入端构成[7-8]，因而MT-HVDC系统可以形成多种的网络结构，接口变换器可以通过串联或并联的方式形成不同的MT-HVDC网络结构。根据网络的连接方式将MT-HVDC系统的网络结构分为两大类，即放射状和网状结构[9-11 ]。网状结构可以增加系统电能传输的冗余度，提高输电线路的可靠性[12-13]，因此被广泛应用于MT-HVDC系统中。在网状结构的MT-HVDC系统中负荷分配方式和分配的比例优化问题越来越受到人们的重视，因此应确定合理的负荷分配比例以使得直流系统能高效运行。目前，已有文献提出了负荷分配控制方法，例如主从控制、平均电流控制等。考虑到各直流终端之间可能相距较远，以及输电线路阻抗和通信延迟会影响控制系统的稳定性，因此，下垂控制是一种合适的负荷分配方法。然而，下垂控制具有两点不足[14-15]：首先下垂控制是通过调节直流母线电压的设定值改变变换器输出功率，因此在其实现过程中，不可避免的会引入母线电压跌落。其二，在MT-HVDC系统中，存在负荷功率分配精度问题。由于直流输电系统中无需考虑无功功率，因此分配精度问题主要体现在有功功率上。因此有必要解决这个难题以增强下垂控制的控制性能，文献[16]提出了一种改进的下垂控制方法，该方法可同时有效地补偿电压跌落并增强负载电流分配精度，但此方法通信压力大，并没有考虑系统存在的网状结构，只适用于低电压微网的输电线路，没有考虑高压直流输电线路中电感和电容参数的影响，因此对MT-HVDC系统而言讨论是不够的。针对网状多端高压直流输电系统，本文基于改进型下垂控制方法，充分考虑线路中电感和电容参数的影响，对系统线路损耗进行最小化，讨论改变直流输电线路的阻抗参数和通信延时情况下的负荷分配，并通过仿真验证所提出方法的稳定性和有效性。

1　网状结构MT-HVDC系统分析

直流输电系统的动态特性对其连续稳定运行起着关键的作用，尤其是直流输电线路的参数电阻、电感和电容对控制系统稳定性的影响。输电线路可以通过级联相同的π型等效电路而成[17]，网状结构的MT-HVDC系统的等效简化模型如图1中。

网状结构中Z12和Z23是不同换流站之间直流输电线路的等效阻抗，ZL1和ZL3表示不同换流站与负载之间直流输电线路的等效阻抗。

图1为网状结构MT-HVDC系统直流侧回路的等效电路，接口变换器和负载侧电压的关系如下：

(1)

式中Zp是#2换流器和负载之间直流电缆的并联阻抗，表达式为

(2)

根据等效电路图1，可以得到负载电流iload：

(3)

式中C13L=C1L+C3L。

根据式(1)，负载电压由负载电流iL和其电阻RL的乘积计算得到，网状结构MT-HVDC系统的多个换流器直流侧输出电流为

(4)

矩阵YM是网状结构中直流系统回路的一个3×3的导纳矩阵。

图1　网状结构多端HVDC的简化模型Fig.1　Simplified model of meshed configuration MT-HVDC

2　改进的下垂控制优化方法

2.1改进的下垂控制方法

传统下垂控制中电压电流的关系为[18]

(5)

根据式(5)，可以看到直流侧输出电压的给定值随着直流输出电流的增加而线性减小。由于MT-HVDC系统的直流回路仅含有功功率，并且系统中长距离输电线路的线路阻抗对系统回路的有功功率的影响不可忽略，因此负荷的分配比例问题亟待解决。本文通过在传统下垂控制器的基础上添加直流输出电压和电流的平均值补偿控制器，补偿控制器的通信数据在两个相邻换流器之间通过低带宽通信网络传输，通过对下垂控制的改进，式(5)中接口变换器的输出电压参考值变化如下：

(6)

式中:GLPF为低通滤波器，其截止频率 fc被设置为20Hz；Vdc(i-1),Vdc(i+1),Idc(i-1)和Idc(i+1)为换流器#(i-1)和#(i+1)的直流侧输出电压和电流；Gpiv和Gpic分别为补偿电压和电流PI控制器的传递函数，通信延时为Gd。

2.2MT-HVDC系统参数对稳定性的影响

为了保证控制系统的稳定运行，需要分析直流系统输电线路的参数变化和通信延时对控制系统的影响，将式(4)代入式(6)得到：

(7)

(8)

(9)

式中 Yij(i, j=1, 2, 3) 表示关联矩阵YR和YM中的元素。 基于上述理论推导和分析，结合式(7)～(9)，可以得到闭环传递函数。改变传输线路的阻抗参数和通信延迟，通过分析特征方程的闭环极点可以检验网状结构的MT-HVDC系统的稳定性。

网状拓扑的多端HVDC系统的稳定性分析如图2所示，该结构闭环传递函数只有4个闭环主导极点。从图2(a) 可以看到，极点1～4固定在虚轴的左边，尽管直流输电线路的电容参数增加到了0.6μF/km，也不会对其控制系统的稳定性有所影响。

线路电感参数变化对系统稳定性的影响如图2(b)所示。极点P1和P2向虚轴移动，这些路径的终点都远离虚轴。极点P3和P4均保持在s域的左半平面，位置未发生太大的变化。因此，无论直流电缆电感如何变化，系统总是稳定的。

线路电阻参数变化情况下闭环主导极点如图2(c)所示，当其他参数固定，而电阻值从0.03Ω/km上升到0.07Ω/km时，除路径IV外的所有路径都向虚轴移动，这与电容和电感变化下的情况不同。然而，尽管电阻值已经大到0.07Ω/km，路径仍然保持在s域的左半平面。因此，在合理范围内不同的线路电阻都能保证系统的稳定。

图2　网状拓扑不同参数下的闭环主极点 Fig.2　Closed loop main poles of different parameters in meshed topology

2.3电力线路损耗最优化

为了降低系统损耗，提高能源的利用效率，本节提出了一种优化的负荷电流分配比例策略，该策略包含两步：第一步，以电力损耗最小化为目标，建立一个最优化模型来确定各直流端输出电压；第二步，以优化的直流电压为基础，由式(7)～(9)得到负荷电流的分配比例k1∶k2∶ k3。

在网状拓扑中，vdcL1和vdcL3是换流器#1(#3)和负载之间的线路压降，vdc12和vdc23是换流器#1，#2和#3之间的线路压降。RL1和RL3分别是换流器#1(#3)和负载之间线路的等效电阻，R12和R23分别是换流器#1(#3)和换流器#2之间输电线路的等效电阻。

s.t.

(10)

式中：λ1是网状结构中传输线路上的总的功率损耗。RL是负载电阻，VLmax和VLmin分别是负载电压的上下限，Vdcmin和Vdcmax是变换器#i的直流电压最大值和最小值。

基于上述优化过程得到的最优的直流端输出电压，负荷电流分配比例k1、k2和k3可由式(7)～(9)计算得到。图3描述了所提出的改进型下垂控制最优的负荷分配比例的控制策略框图。

图3　基于改进型下垂控制方法的最优负荷分配比例框图Fig.3　Block diagram of optimal load distrbution based on improved droop control method

3　仿真结果

为了验证所提出控制方法在MT-HVDC系统中的有效性，利用MATLAB/Simulink仿真软件在网状结构MT-HVDC系统中对本文提出的控制方法和最优的负荷分配进行验证。系统参数如表1所示。

图4(a)显示了网状结构下电压调整和负荷电流分配的暂态响应，此时通信延时τ被调整到1s，直流输电线路长度分别为lL1=100km、l12=70km、l23=60km、lL3=120km。补偿控制器在t=2s时投入，各换流器的直流输出电流逐渐得到调整，与分析计算得到的最优的负荷电流分配比例相匹配，即k1∶k2∶k3≈1∶0.05∶0.74。同时，直流侧平均电压提升了2.54kV。 然而，3个换流器的直流输出电压偏差的最大值仍保持在额定电压参考值的5%以内，系统经过2s的调整时间后达到稳定。

表1　系统的基本参数

图4(b)增加直流输电线路长度后，直流输出平均电压偏差从2.54 kV上升到了5.32 kV。然而，平均电压依然保持在换流器输出电压的安全范围内。由于线路长度的变化，负荷分配比例随之变化为k1∶k2∶k3≈1∶0.03∶0.88。

(a)lL1=100 km, l12=70 km, l23=60 km, lL3=120 km, τ=1 s

(b)lL1=150 km, l12=120 km, l23=110 km, lL3=170 km, τ=1 s

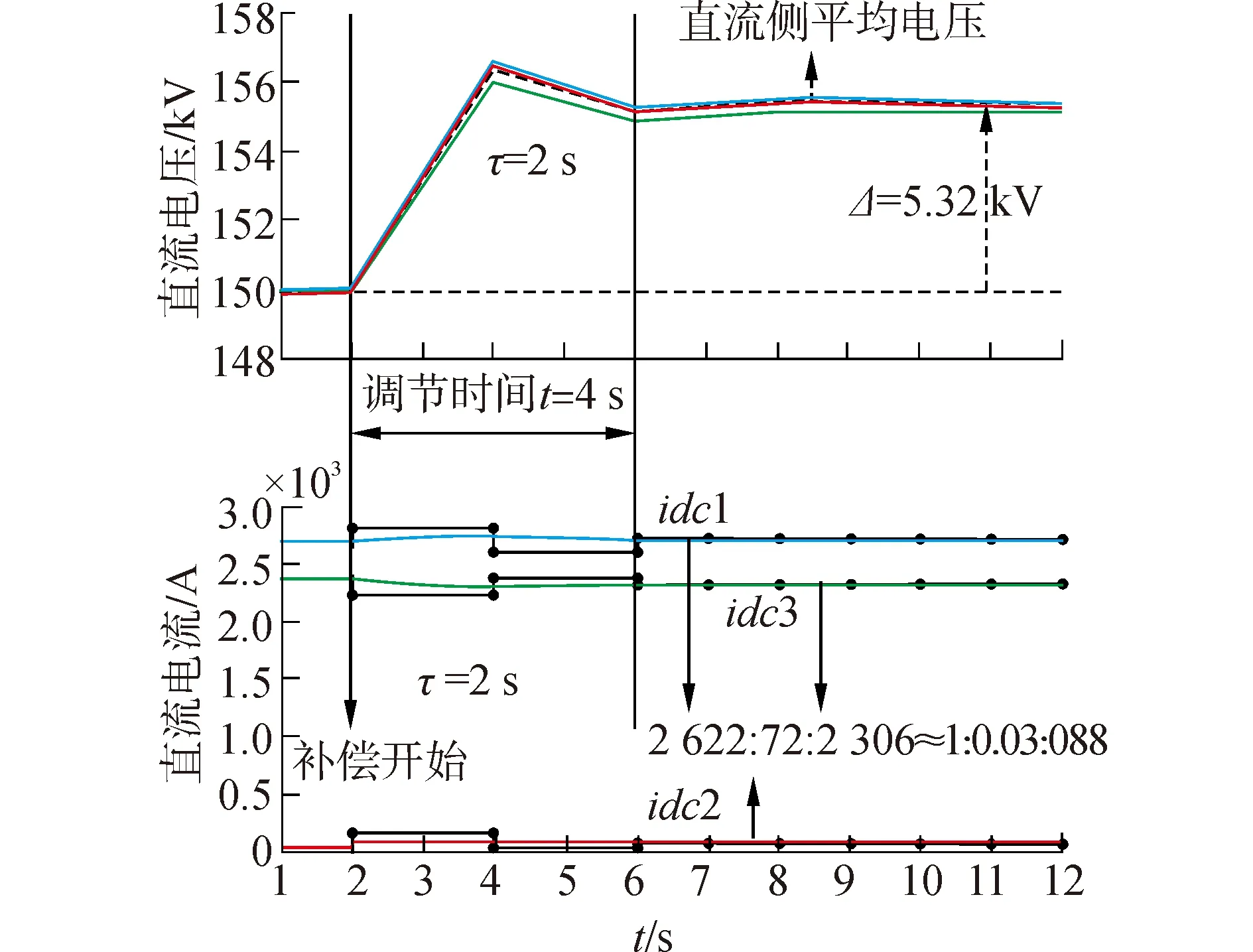
(c)lL1=150 km, l12=120 km, l23=110 km, lL3=170 km, τ=2 s图4　网状结构系统的暂态响应Fig.4　Transient response of meshed configuration MT-HVDC system

图4(c)的仿真结果验证了当线路长度保持不变，通信延迟τ的增加只会对暂态调整时间产生影响，控制系统需要4 s来实现平衡和稳定运行。同时，负荷电流分配比例与图4(b)保持一致。进一步可以验证输电线路长度对负荷电流比例分配精度的影响。

4　结论

本文基于改进型下垂控制方法，研究了负荷分配比例的优化，实现了多端HVDC系统中直流输电系统的线路损耗最小化，提高能源利用效率。具体结论如下：

1) 通过级联n个相同的π型电路，等效了MT-HVDC系统网状结构下的简化模型；并且得到了换流器#1～ #3直流侧输出电流和电压之间的关系。

2) 利用两相邻换流器的电压和电流数据实现了分布式控制，该方法减少了低带宽通信系统的通信压力。

3) 当分别改变直流输电线路的阻抗参数和通信延时时，闭环主极点始终保持在s域的左半平面，从而可以确保控制系统的稳定性，证明了提出的控制方法的有效性。

4) 通过最小化输电线路损耗得到最优的负荷电流分配比例。同时，直流输出电压平均值可以被提升到额定参考值，且每个电压都可保证在电网正常运行的范围内。

[1]CHAUDHURI N R, MAJUMDER R, CHAUDHURI B. System frequency support through Multi-terminal DC (MTDC) grids[J]. IEEE transactions on power systems, 2013, 28(1): 347-356.

[2]FU Yuan, WANG Yi, LUO Yingli, et al. Interconnection of wind farms with grid using a MTDC network[C]//Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society. Montreal, QC, 2012: 1031-1036.

[3]张新燕, 孟瑞龙, 梅生伟, 等. 含大规模风电送端系统对直流系统的影响[J]. 高电压技术, 2015, 41(3): 730-738.

ZHANG Xinyan, MENG Ruilong, MEI Shengwei, et al. Impact on HVDC systems by the sending AC system with large-scale wind farms[J]. High voltage engineering, 2015, 41(3): 730-738.

[4]张文亮, 汤涌, 曾南超. 多端高压直流输电技术及应用前景[J]. 电网技术, 2010, 34(9): 1-6.

ZHANG Wenliang, TANG Yong, ZENG Nanchao. Multi-terminal HVDC transmission technologies and its application prospects in China[J]. Power system technology, 2010, 34(9): 1-6.

[5]LI Chenghao, ZHAN Peng, WEN Jinyu, et al. Offshore wind farm integration and frequency support control utilizing hybrid multiterminal HVDC transmission[J]. IEEE transactions on industry applications, 2014, 50(4): 2788-2797.

[6]DENG Fujin, CHEN Zhe. An offshore wind farm with DC grid connection and its performance under power system transients[C]//Proceedings of the 2011 IEEE Power and Energy Society General Meeting. San Diego, CA, 2011: 1-8.

[7]赵成勇, 胡冬良, 李广凯, 等. 多端 VSC-HVDC 用于风电场联网时的控制策略[J]. 电网技术, 2009, 33(17): 135-140.

ZHAO Chengyong, HU Dongliang, LI Guangkai, et al. Control strategy for inter connection of wind farms by multi-terminal VSC-HVDC[J]. Power system technology, 2009, 33(17): 135-140.

[8]张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010, 30(25): 1-9.

ZHANG Liying, YE Tinglu, XIN Yaozhong, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE, 2010, 30(25): 1-9.

[9]BEERTEN J, COLE S, BELMANS R. Modeling of multi-terminal VSC HVDC systems with distributed DC voltage control[J]. IEEE transactions on power systems, 2014, 29(1): 34-42.

[10]KALCON G O, ADAM G P, ANAYA-LARA O, et al. Small-signal stability analysis of multi-terminal VSC-based DC transmission systems[J]. IEEE transactions on power systems, 2012, 27(4): 1818-1830.

[11]PINTO R T, BAUER P, RODRIGUES S F, et al. A novel distributed direct-voltage control strategy for grid integration of offshore wind energy systems through MTDC network[J]. IEEE transactions on industrial electronics, 2013, 60(6): 2429-2441.

[12]ZHANG Xiaoping, REHTANZ C, PAL B. Flexible AC transmission systems: modelling and control[M]. Berlin: Springer, 2012.

[13]KREIKEBAUM F, DAS D, HERNANDEZ J, et al. Ubiquitous power flow control in meshed grids[C]//Proceedings of IEEE Energy Conversion Congress and Exposition. San Jose, CA, 2009: 3907-3914.

[14]阎发友, 汤广福, 贺之渊, 等. 基于 MMC 的多端柔性直流输电系统 改进下垂控制策略[J]. 中国电机工程学报, 2014, 34(3): 397-404.

YAN Fayou, TANG Guangfu, HE Zhiyuan, et al. An improved droop control strategy for MMC-based VSC-MTDC systems[J]. Proceedings of the CSEE, 2014, 34(3): 397-404.

[15]谢玲玲, 时斌, 华国玉, 等. 基于改进下垂控制的分布式电源并联运行技术[J]. 电网技术, 2013, 37(4): 992-998.

XIE Lingling, SHI Bin, HUA Guoyu, et al. Parallel operation technology of distributed generations based on improved droop control[J]. Power system technology, 2013, 37(4): 992-998.

[16]LU Xiaonan, GUERRERO J M, SUN Kai, et al. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy[J]. IEEE transactions on power electronics, 2014, 29(4): 1800-1812.

[17]LIN S C, YEH C Y. Microstrip branch-line coupler with optimized spurious suppression based on cascaded PI-type equivalent transmission lines[C]//Proceedings of IEEE International Workshop on Electromagnetics. Sapporo, 2014: 195-196.

[18]徐瑞林, 徐鑫, 郑永伟, 等. 基于改进下垂控制的微网运行控制策略[J]. 电力系统及其自动化学报, 2012, 24(6): 14-19.

XU Ruilin, XU Xin, ZHENG Yongwei, et al. Improved droop control scheme for micro-grid operation[J]. Proceedings of the CSU-EPSA, 2012, 24(6): 14-19.

本文引用格式：

冷欣,宋文龙，刘一琦, 等. 网状多端高压直流输电系统负荷分配优化控制[J]. 哈尔滨工程大学学报, 2016, 37(8): 1118-1123.

LENG Xin, SONG Wenlong, LIU Yiqi, et al. Optimal control of load distribution in a meshed multiterminal high-voltage DC transmission system[J]. Journal of Harbin Engineering University, 2016, 37(8): 1118-1123.

Optimal control of load distribution in a meshed multiterminal high-voltage DC transmission system

LENG Xin1, SONG Wenlong1, LIU Yiqi1, WAMG Rui2, WANG Lihui3

(1. College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China; 2. Wireless Optimization Room, Harbin Mobile Communication Company, Harbin 150001, China; 3. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

To ensure minimum line loss in a high-voltage DC (HVDC) transmission system for a multiterminal HVDC transmission system of meshed configuration, an optimal load distribution method based on modified droop control is presented in this paper. Average DC output voltage and output current of two neighboring converters are applied to the conventional droop control. At the same time using the low-bandwidth communication network, the DC bus voltage is improved and the optimal distribution of load power for different line impedance values is achieved. This study also analyzes the application of the control method using different line impedance values and communication delays. Simulation results show that the load distribution of the mesh multiterminal HVDC transmission system is optimized under different conditions and achieves optimization and stability of the system. The proposed method maintains maximum values for DC output deviation within 5% of the rated voltage reference value, thus ensures line loss minimization of the network multiterminal HVDC system and improves the energy utilization efficiency.

multiterminal high-voltage DC (MT-HVDC); load distribution; meshed configuration; droop; low-bandwidth communication; line loss minimization; optimal control

2016-02-15.网络出版日期：2016-07-11.

国家自然科学基金项目(51477028)；中央高校基本科研业务费专项资金项目(DL11BB34)；黑龙江省博士后资助经费(LBH-Z12010).

冷欣 (1980-), 女, 讲师, 博士；

宋文龙(1973-),男，教授，博士生导师.

宋文龙, E-mail:wlsong139@163.com.

10.11990/jheu.201602016

TP29

A

1006-7043(2016)08-1118-06