基于磁梯度张量的共轭梯度3D约束反演
李金朋,张英堂,范红波,李志宁,尹 刚
(解放军军械工程学院,河北 石家庄 050003)
基于磁梯度张量的共轭梯度3D约束反演
李金朋,张英堂,范红波,李志宁,尹刚
(解放军军械工程学院,河北 石家庄050003)
针对传统铁磁物质反演方法存在反演结果多解性的问题,提出了基于磁梯度张量的共轭梯度3D约束反演方法。该方法在经典Tikhonov正则化理论框架下,引入粗糙度矩阵对反演模型进行约束以避免反演过程中的多解性问题;针对磁梯度张量数据深度分辨率差、容易出现“趋肤效应”的问题,在模型目标函数中引入深度加权矩阵提高纵向分辨率;通过引入惩罚泛函,在反演迭代过程中去除方程的病态解,使反演结果更好地与原始模型相吻合。仿真验证表明:该反演方法能够反映磁性异常体的轮廓形态,具有较好的横向和纵向分辨率。
磁梯度张量;共轭梯度;粗糙度矩阵;深度加权矩阵
0 引言
磁性目标反演技术是通过地面或航空等实测数据,利用某种手段推算出磁性体(未爆弹、水雷、潜艇等)在地下的分布信息。磁法勘探具有探测精度高、虚警率低、定位能力强等优点。运用磁探测技术可以对地下或者水下小尺度磁性目标进行定位与识别[1],为下一步的工作提供数据支持。磁梯度张量场是指磁场三分量在三个坐标方向上的变化率,共有9个分量。相比磁总场、磁总场梯度和磁场三分量数据,磁梯度张量场不但具有更高的分辨率,而且包含可以联合解释的多个分量,能更好地描绘场源的空间形态及位置[2]。
国内外众多研究学者针对三维反演成像展开了大量的工作。1972年,Nabighian将解析信号运用到二维剖面磁场数据解释中,随后又应用于三维网格情况[3-4]。2013年,吉林大学孟慧在磁梯度张量数据解释方面研究了解析信号法,通过仿真实验表明解析信号法能突出浅部磁场特性[5]。1982年,Thompson利用二维欧拉反褶积识别法对二维剖面数据进行解释。1990年,Reid等人将二维反演方法推广到三维磁场数据解释中,能够对大范围的平面网格数据进行反演[6-7]。2008年,吴招才将该方法应用到多目标识别,仿真表明识别效果较好[8]。1997年由Patella[9]首次提出概率成像法。郭良辉根据概率成像概念提出了重力数据三维相关成像法并将其推广到磁法数据的相关成像,提出了磁总场异常相关成像法,并通过建模仿真验证了该方法的有效性[10-11]。2002年,Portniaguine和Zhdanov提出了聚焦反演法,并将其应用于磁化率成像和重力梯度反演[12-13]。
但是,以上反演方法研究存在方程解的不唯一性及成像结果的“上漂”现象等问题,使得传统反演方法在实际应用中受到限制。针对此问题,本文提出基于磁梯度张量的共轭梯度3D约束反演。
1 磁梯度张量正演理论
1.1磁梯度张量要素
与传统的磁总场异常相比,磁梯度张量能提供更加丰富的异常信息,能更好的反映地下磁性体的细节特征。磁梯度张量可以由一个二阶矩阵表示为:
(1)
式(4)中:G为磁梯度张量;Bαβ(α,β=x,y,z)为磁梯度张量的分量,共有9个;根据场论可知:Bxy=Byx,Bxz=Bzx,Byz=Bzy,Bxx+Byy+Bzz=0。因此,磁梯度张量的9个分量只有5个是独立的。
1.2长方体正演公式
建立笛卡尔坐标系。x,y轴为水平轴,z轴为垂直向上轴。设x方向为a,y方向为b,z方向为c的直立长方体,长方体中心坐标为(x0,y0,z0)。M为长方体磁化强度,点(x,y,z)为观测点。则长方体磁异常及梯度正演公式如下:
(2)
(3)
(4)
(5)
(6)
(7)
式中,cosαs,cosβs,cosγs为磁化强度M的方向余弦,u0为真空磁导率,(ξ,u,ζ)为长方体单元角点坐标。
2 基于磁梯度张量的共轭梯度3D约束反演
将地下待测空间划分成大小相等、紧密排列、物性参数为常数且相等的长方体,观测点与单元体中心到地面的投影一一对应,各观测点实际测量所得磁梯度张量分量数据为所有长方体相应分量的和,用线性公式表示为:
d=A×m
(8)
式(8)中,矩阵A的元素Aij为第i(i=1,2,3,…,p)个观测点观测的第j(1,2,3,…,n)个单元的响应;p×1维的行向量d为任意张量分量数据,m为待反演参数。
传统的磁梯度张量场反演等价于求解线性方程(8)的反问题,由于采集数据d远小于待反演参数m,因此该方程是欠定的,方程组的解不唯一且不稳定。根据Tikhonov正则化理论,构建三维目标函数:
(9)
2.1粗糙度矩阵
针对病态方程的多解性问题,本文将模型粗糙度矩阵引入磁梯度张量的三维反演中,通过补充先验数据信息,将目标函数转化为非病态问题,使得反演模型能够在三个方向上光滑过渡。定义粗糙度矩阵R为m(r)在x,y和z方向的一阶偏微分的平方和,即:
(10)
2.2深度加权矩阵
根据磁梯度张量正演公式(2)—式(7)可知,反演方程的核函数随着距离的增大而快速衰减,而在构造极小化模型目标函数‖m‖2=∫m2dV时,重构模型的核函数是线性的。因此如果不对模型进行约束就会使反演结果出现“趋肤效应”,在进行模型重构时使模型多集中于地表很难反演出真实构造。因此,本文通过引入深度加权因子来抵消核函数随深度增大的衰减量,即:
(11)
式(11)中,z为地下网格单元体中心坐标;z0和β为常数。β为经验值一般取2~4;z0取决于块体单元的尺寸以及观测面的高度。
将公式(11)及目标函数最小化模型构造带入公式(10):
(12)
式(12)中,αs,αx,αy和αz为模型目标函数中的加权因子。将公式(12)按照模型区域网格剖分进行离散化得到:
(13)
式(13)中,Wi=αiRiZ(i=s,x,y,z)。Ri为有限元差分算子,Z为深度加权对角矩阵。将公式(13)代入式(9):
(14)
2.3惩罚泛函
在反演过程中,为了得到与实际情况更加吻合的物性参数分布,利用惩罚函数在反演迭代过程中去除病态解,对模型参数进行约束使反演结果控制在合理的范围内:
(15)
2.4共轭梯度法
共轭梯度法是求解大型对称正定线性方程最优化问题的高效解法。共轭梯度法最早是由计算数学家Hestenes和几何学家Stiefel于1952年在解线性方程组时提出的。
其主要思想是,对称正定线性方程组
Ax=b
(16)
的解与下述二次函数F(x)的极小值等价,
(17)
共轭梯度法就是基于这个二次函数推导得出的,过程从略,算法如下:
1)任意取初始向量x0,计算r0=b-Ax0,并取p0=r0。
2)对k=0,1,…,计算下列各项,
3)若‖rk+1‖≤ε,则停止计算,否则返回2)。
3 仿真分析
3.1单直立长方体模型
设地下模型空间尺寸xyz为21 m×21 m×10 m,将地下场源空间划分为21×21×10=4 410个单元格,每个单元格均为边长为1 m的正方体,地面观测点为21×21=441个网格。地下空间存在1个异常体,长×宽×高为4 m×5 m×4 m,顶板埋深为3 m,底板埋深为7 m,磁化强度为40 A/m,模型与观测点如图1所示。假设模型体在垂直磁化条件下,观测面位于地面0.1 m处,得到理论模型正演数据如图2所示。利用所得正演数据,在仅考虑数据拟合泛函时,对理论模型进行反演。设置最高迭代次数为60次。对反演物性参数设置解区间[Mmax,Mmin],在本例对磁梯度张量全张量反演获得的磁化强度进行加权并设置统一的模型约束区间为[1,40]。从图3可以看出,异常体反演的结果具有一定的横向分辨率,但是对深度信息的反映较差,长方体反演模型多集中于地表,难以反映异常体的真实构造。
应用本文反演方法,在目标函数中加入深度加权函数及粗糙度矩阵。通过对比图3和图4结果可以看出:在加入深度加权函数和粗糙度矩阵后,能够反映异常的深度信息,更好地反映了地下异常体的分布情况。
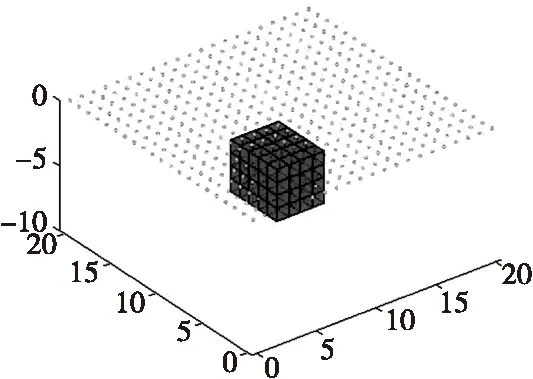
图1 正演理论模型Fig.1 Forward theoretical model

图2 单直立长方体磁梯度张量数据分布图Fig.2 Single rectangular magnetic gradient tensor data map
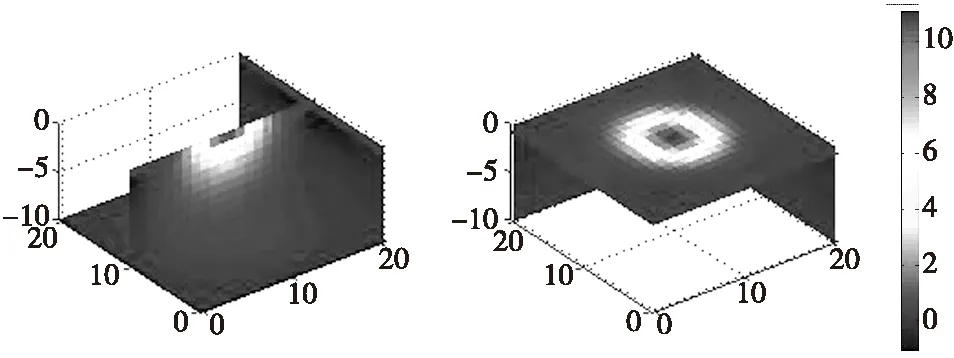
图3 数据拟合泛函反演图Fig.3 data fitting inversion map

图4 应用本文方法进行反演Fig.4 Inversion results by this method
3.2长方体组合模型
设地下模型空间尺寸xyz为21 m×21 m×10 m,将地下场源空间划分为21×21×10=4 410个单元格,每个单元格均为边长为1 m的正方体,地面观测点为21×21=441个网格。地下空间存在2个长方体,分别由长×宽×高为7 m×7 m×7 m和8 m×9 m×9 m的长方体拼接而成,磁化强度为40 A/m,模型与观测点如图5所示。假设模型体在垂直磁化条件下,观测面位于地面0.1 m处,得到理论模型正演数据如图6所示。对反演物性参数设置解区间[Mmax,Mmin],在本例对磁梯度张量全张量反演获得的磁化强度进行加权并设置统一的模型约束区间为[1,40]。利用本文反演方法获得的反演分布如图7所示。从结果可以看出:该反演方法能够反映长方体组合模型的轮廓形态,具有较好的横向和纵向分辨率。
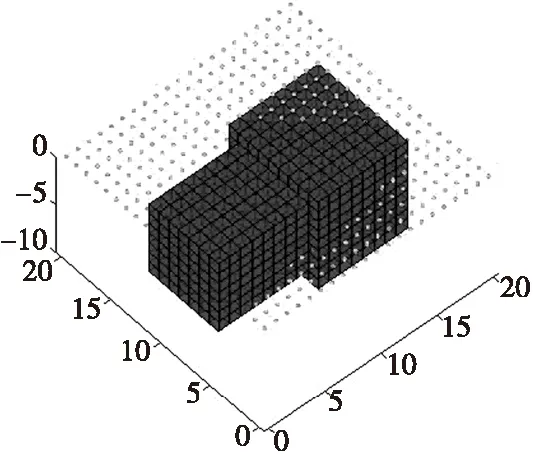
图5 组合长方体模型Fig.5 Combination rectangular model

图6 组合立长方体磁梯度张量数据分布图Fig.6 Combination of rectangular magnetic gradient tensor data map
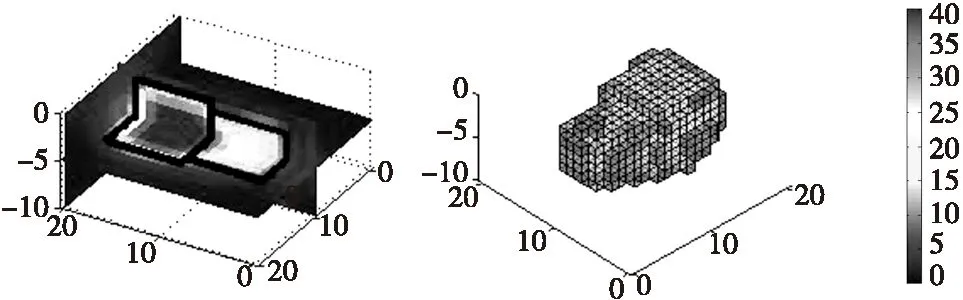
图7 加约束后反演切片图与空间立体结构图Fig.7 Inversion slice and three-dimensional structure under constraint
4 结论
本文提出了基于磁梯度张量的共轭梯度3D约束反演方法。通过引入粗糙度矩阵有效地避免函数的多解性问题;利用深度加权矩阵约束函数,压制了“趋肤效应”,提高了异常体的纵向分辨率;通过引入惩罚泛函,有效提高了解的有效性。仿真验证表明:本文方法能够较好地反映磁性异常体的轮廓形态,具有较好的横向和纵向分辨率。不足之处在于只是通过仿真验证了该方法的有效性,在工程实践中的应用还有待进一步的补充和改进。
[1]卞光浪,翟国军,黄谟涛,等.顾及地磁背景场的多目标磁异常分量换算方法[J].武汉大学学报,2011,36(8):914-918.
[2]张昌达.航空磁力梯度张量测量——航空磁测技术的最新进展[J].工程地球物理学报, 2007,3(5): 354-361.
[3]NabighianMN.Theanalyticsignaloftwo-dimensionalmagneticbodieswithpolygonalcross-section:itspropertiesanduseforautomatedanomalyinterp-retation[J].Geophysics, 1972,37(3):507-517.
[4]NabighianMN.Towardathree-dimen-sionalautomaticinterpretationofpotentialfielddataviageneralizedHilberttransfo-rms:Fundamentalrelations[J].Geophysics.,1984,49(6):780-786.
[5]孟慧.磁梯度张量正演、延拓、数据解释方法研究[D]. 吉林:吉林大学仪器科学与电器工程学院,2012.
[6]ThompsonDT.EULDPH:Anewtechniqueformakingcomputer-assisteddepthestim-atesfrommagneticdata[J].Geophysics,1982,47(1):31-37.
[7]ReidAB,AllsopJM,GranserH,etal.Ma-gneticinterpretationinthreedimensionsusingEulerdeconvolution[J] .Geophysics,1990,55(1):80-91.
[8]吴招才.磁梯度张量技术及其应用研究[D].武汉:中国地质大学,2008.
[9]PatellaD.Introductiontogroundsurfaceself-potentialtomography[J].GeophysicalProspecting,1997,45:653-681.
[10]郭良辉,孟晓红,石磊,等.重力和重力梯度数据三维相关成像[J].地球物理学报,2009,52(4):1098-1106.
[11]郭良辉,孟晓红,石磊.磁异常ΔT三维相关成像[J].地球物理学报,2010,53(2):435-441.
[12]PortinaguineO,ZhdanovMS.Focusinggeophysicalinversionimage[J] .Geop-hysics,1997,64(3):874-887.
[13]PortinaguineO,ZhdanovMS.3-Dinv-ersionwithdatacompressionandimagemagneticfocusing[J].Geophysics, 2002,67,(5):1532-1541.
3D Constrained Inversion of Conjugate Gradient Based on Magnetic Gradient Tensor
LI Jinpeng, ZHANG Yingtang, FAN Hongbo, LI Zhining, YIN Gang
(Ordnance Engineering College, Shijiazhuang 050001, China)
For the problem that the inversion results of conventional inversion methods of ferromagnetic material have multiple solutions due to qualitative equations, we proposed a method of 3D constrained inversion of conjugate gradient based on magnetic gradient tensor. Firstly, in order to avoid the problem of multiple solutions, we used the roughness matrix in the classical Tikhonov regularization under the framework of the theory. Then, for the magnetic gradient tensor data had poor depth resolution and problem of “skin effect”, we used depth weighting matrix introduced in the objective function to improve the vertical resolution. Finally, we removed solution of the equation in the inversion iterative process, so that the inversion results coincided with the original model better, by introducing the penalty functional. Simulation result showed that this inversion method could reflect the outline shade of the magnetic anomaly and has good lateral and vertical resolution.
magnetic gradient tensor; conjugate gradient; roughness matrix; depth weighting matrix
2016-01-13
李金朋(1991—),男,吉林长春人,硕士研究生,研究方向:测试技术与信号处理。E-mail:18626648671@163.com。
P631
A
1008-1194(2016)04-0088-05

