与对称点和共轭点有关的螺旋函数子类的系数估计
汤 获,王晓英
(1.赤峰学院 数学与统计学院;2.赤峰学院 应用数学研究所,内蒙古 赤峰 024000)
与对称点和共轭点有关的螺旋函数子类的系数估计
汤获1,2,王晓英1
(1.赤峰学院数学与统计学院;2.赤峰学院应用数学研究所,内蒙古赤峰024000)
本文引入与对称点和共轭点有关的螺旋函数新子类Ms(θ,A,B)和Mc(θ,A,B),讨论了这些子类的系数估计,所得结果推广了一些已知结论.
对称点;共轭点;螺旋函数;星象函数;系数估计
1 引言与预备知识
令U表示在单位开圆盘D={z:|z|<1}内单叶解析且具有如下形式

的函数类,且满足条件ω(0)=0,|ω(z)|<1,z∈D.
令S表示在D内单叶解析且具有如下形式

的函数类.
另外,设Ss*是(1.1)式给出的函数所构成的S的子类,并且满足
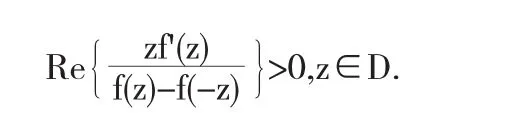
这类函数称为关于对称点的星象函数,该定义是在1959年由Sakaguchi[1]给出的.1987年,Ashwah和Thomas[2]给出了关于共轭点的星象函数类Sc*,其定义如下:
设Sc*是由(1.1)式给出的函数构成的S的子类,并且满足条件
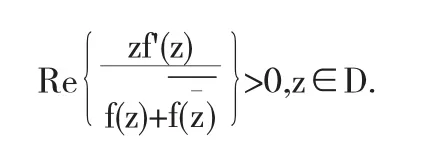
假设函数f和g在D内解析,若存在一个Schwarz函数ω(z),使得ω(0)=0,|ω(z)|<1满足g(z)=f(ω(z),z∈D,那么,我们就称函数g从属于f,记作g(z)≺f(z),z∈D.
利用上述从属定义,Goel和Mehrok在文[3]中引入了函数类Ss*的子类Ss*(A,B).
定义1.1设函数f由(1.1)式给出,并且满足条件
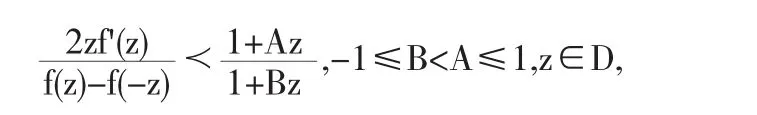
则记此函数类为Sc*(A,B).
以同样的方式,汤获和邓冠铁在文[4]中引入了函数类Sc*的子类Sc*(A,B),并讨论了该函数子类的系数估计.
定义1.2[4]设函数f由(1.1)式给出,并且满足条件

则记此函数类为Sc*(A,B).
在此基础上,本文我们主要考虑更一般的螺旋函数子类Ms(θ,A,B)和Mc(θ,A,B),并讨论这些函数类的系数估计,所得的结果推广了一些已知结论.
定义1.3设函数f由(1.1)式给出,并且满足条件

则记此函数类为Ms(θ,A,B).
定义1.4设函数f由(1.1)式给出,并且满足条件
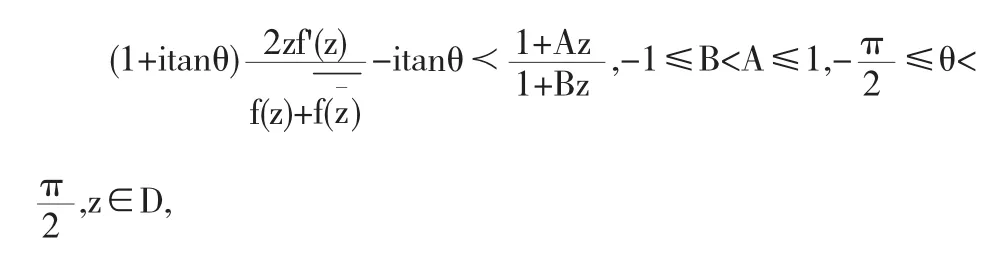
则记此函数类为Mc(θ,A,B).
我们注意到,若合适选取参数θ,A和B,我们可得下列已知函数类.
(i)Ms(0,A,B)=Ss*(A,B)(见文[3]),Mc(0,A,B)=Sc*(A,B)(见文[4]);
(ii)Ms(0,1,-1)=Ss(*见文[1]),Mc(0,1,-1)=Sc(*见文[2]).利用定义1.3,定义1.4和从属定义,我们易知:
(1)f∈Ms(θ,A,B)当且仅当

(2)f∈Mc(θ,A,B)当且仅当

为了证明本文的主要结果,我们需要下列引理.
引理1.1[4]如果p(z)是由(1.4)给出,那么

2 主要结果
定理2.1 设f∈Ms(θ,A,B),则对于n≥1,有
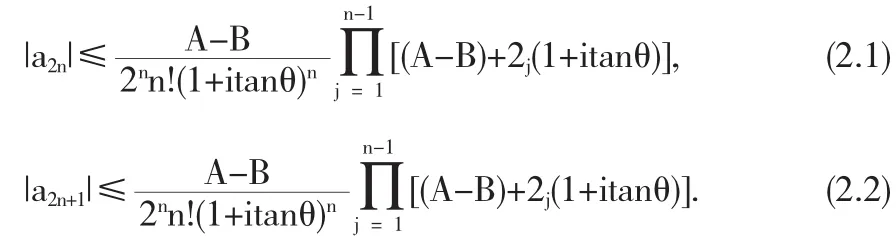
证明由(1.2)式和(1.4)式,我们易得

比较上式两边z的幂的系数,我们可得
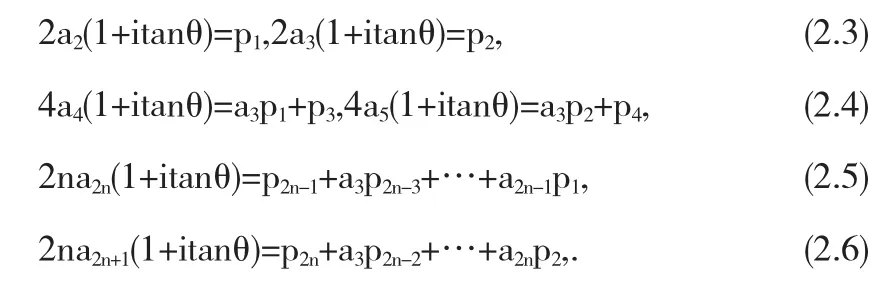
利用(2.3)式和引理1.1,我们易得

再利用引理1.1(,2.4)式和(2.7)式,我们可得

当n=1,2时,(2.1)式和(2.2)式显然成立.接下来,我们利用数学归纳法来证明(2.1)式.
由(2.5)式和引理1.1,我们得到

假设当k=3,4,…,(n-1)时(,2.1)式成立,那么由(2.8)式,我们可以得到

为了完成证明,我们需证当m=3时
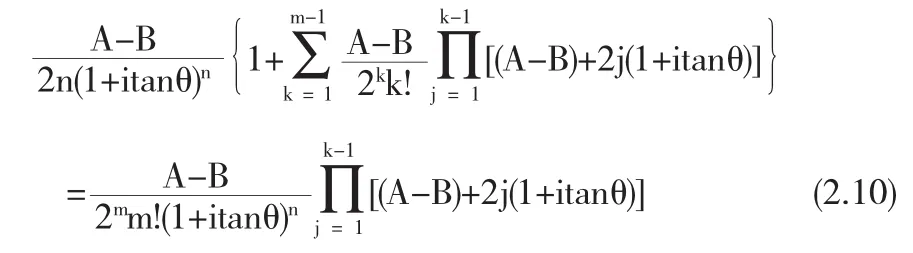
成立即可.
假设对所有m,3<m≤(n-1)(,2.10)式成立,那么利用(2.9)式,我们可得
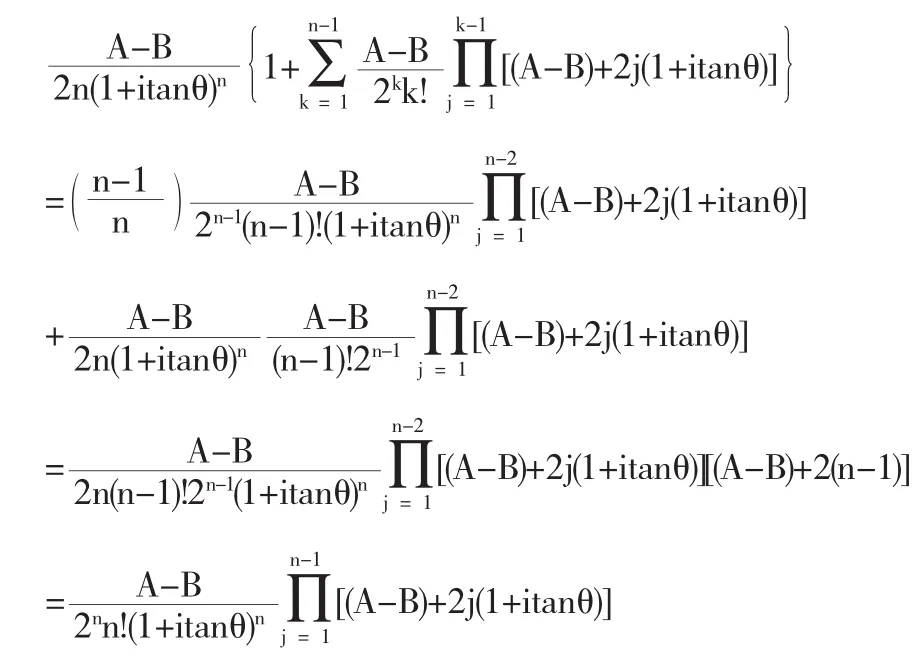
因此,当m=n时(,2.10)式成立,即(2.1)式也成立.同理,我们可以证明(2.2)式成立.
在定理2.1中,若取θ=0,则有下面的推论2.1.
推论2.1设f∈Ms(0,A,B)≡Ss*(A,B),则对于n≥1,有
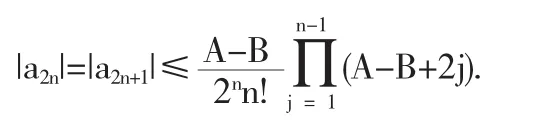
在推论2.1中,若取A=1,B=-1则有下面的推论2.2.
推论2.2设f∈Ms(0,1,-1),则对于n≥1,有

定理2.2设f∈Mc(0,A,B),则对于n≥1,有

证明由(1.3)式和(1.4)式,我们易得

比较上式两边z的幂的系数,我们可得


再利用引理1.1(,2.14)式,(2.15)式和(2.18)式,我们可得利用(2.13)式和引理1.1,可得


当n=1,2时(,2.11)式显然成立.下面,我们借助数学归纳法来证明(2.11)式.
由(2.16)式和引理1.1,我们得到

假设当k=3,4,…,(n-1)时,(2.11)式成立.由(2.19)式,我们可以得到

要想完成该证明,只需证当m=3时成立即可.
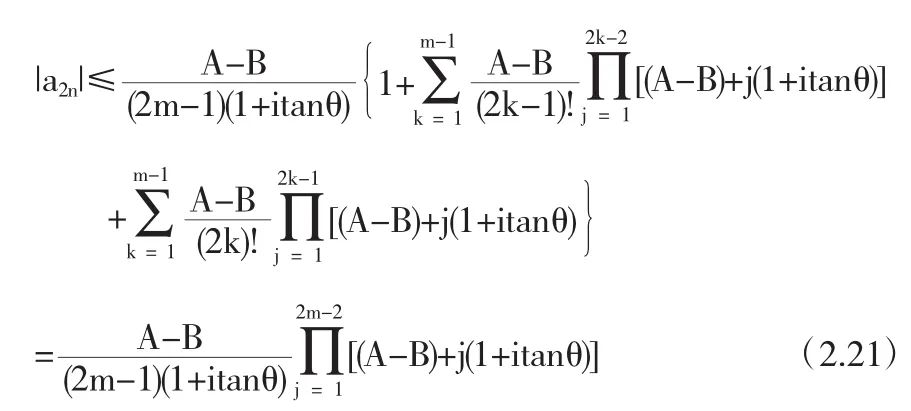
假设对所有m,3<m≤(n-1),(2.21)式成立.由(2.20)式,我们有


因此,当m=2时,(2.21)式成立,即证(2.11)式成立.同理,我们可以证明(2.12)式成立.
在定理2.2中,若取θ=0,则有下面的推论2.3.

推论2.3设f∈Mc(0,A,B)≡Sc*(A,B),则对于n≥1,有在推论2.3中,若取A=1,B=-1,则有如下的推论2.4.推论2.4设f∈Mc(0,1,-1)≡Sc*,则对于n≥1,有
〔1〕Sakaguchi K.On certain univalent mapping[J].Math. Soc.,Japan,1959,11:72-75.
〔2〕El-Ashwah R M,Thomas D K.Some subclasses of close-to-convex functions[J].J.Ramanujan Math.Soc.,1987,2:86-100.
〔3〕Goel R M,Mehrok B C.A subclass of starlike functions w ithrespect tosymmetric points[J].Tamkang Journal of Mathematics,1982,13:11-24.
〔4〕Huo Tang,Guantie Deng.Coefficient estimates for subclasses of analytic functions w ith respect to other points [J].Tamkang Journal of Mathematics,2013,44:141-148.
O174.13
A
1673-260X(2016)08-0001-03
2016-05-11
国家自然科学基金资助项目(11561001;11271045);内蒙古自然科学基金资助项目(2014MS0101;2010MS0117);内蒙古高校科研基金资助项目(NJZY240;NJZY16251)

