数形结合 深挖内涵 明晰概念——“平均数”教学实践与思考

浙江德清县实验学校（313200） 朱东亮

数形结合深挖内涵明晰概念
——“平均数”教学实践与思考

浙江德清县实验学校（313200） 朱东亮

数学概念是构建数学理论大厦的基石，是数学学科的灵魂和精髓。因此，教师应重视概念教学，通过数形结合等途径，引导学生深入挖掘概念的内涵，明晰所学的概念，真正掌握所学的知识。

概念教学平均数思维冲突价值几何直观意义内涵特性

对概念清晰而又深刻的理解是学好数学的关键，是应用数学知识解决问题的基础。平均数是一个重要的刻画数据集中趋势的统计量，小学数学中所讲的平均数一般是指算术平均数，也就是一组数据的和除以这个数据的个数所得到的商。平均数既可以反映一组数据的一般情况，也可以用它进行不同组数据的比较，从而看出组与组之间的差别。下面，我以“平均数”一课教学为例，尝试探讨概念教学的方法。

一、设置思维冲突，体会平均数的价值

学生对通过比较总数判断两组数据水平的高低有着丰富的经验，因此，教师教学时可以先出示图1，让学生判断在踢毽子比赛中哪个队获胜。然后教师参加到男生队中（师踢了13个），并提问“通过比较总数来判断哪个队获胜公平吗”，以激发学生的思维冲突，引导学生提出用平均数来判断。虽然平均数是一组数据本身就具有的属性，不依赖于比较存在，但根据学生的思维水平和特点，采用这样的引入方式可以让学生充分感受到比总数的局限性，体会到平均数产生的必要性和价值。这对激发学生学习概念的兴趣，比较不同概念之间的联系与区别有着重要作用。

图1　

图2　

二、利用几何直观，理解平均数的意义

华罗庚说过：“数缺形时时少直观，形缺数时难入微。”“平均数”一课的教学，可采用数形结合的方式进行。平均数是刻画数据集中趋势的统计量，反映了一组数据中心点的位置所在，这是平均数统计意义的核心。因此，让学生经历一组数据中心点的产生过程，有助于学生理解平均数的概念。具体可以采用“移多补少”的方法让学生体会这个过程：3名女生踢毽子的个数如图3，通过计算得出女生队踢毽子的平均数是14个。然后引导学生通过“移多补少”的方法找到平均数，再将平均数直观地展现在学生眼前，如图4。通过图形的直观展示，学生对平均数的产生过程有了切实的体会，从而对平均数反映一组数据的一般水平也就有了更深刻的认识。

图3　

图4　

三、挖掘概念内涵，明晰平均数的特性

根据平均数的概念，平均数具有某些与生俱来的特性，主要包括敏感性、集中性、虚拟性三个方面。通过适当的学习材料，让学生明晰平均数的特性，有助于学生加深对概念的理解。

1.敏感性

平均数的敏感性是指每个数据的变化都对平均数产生影响。教师可以通过改变其中一个数据的大小，让学生体会这一特性。如在数据12、11、16、13中，如果将13变成17，那么平均数将从13变成14，使学生明确当个体数据变大时，平均数将被拉升；反之，平均数将被拉低。从平均数的敏感性，教师还可以引导学生发现平均数容易受极大（小）值的影响。如下表中小明的平均分显然受到100分的影响，从而拉高了平均数。这样可让学生体验到平均数的局限性，了解生活中经常采用去掉部分极值后再求平均数的原因。

在一次唱歌比赛中，小明的平均得分是70分，小乐的平均得分是67分，小明的唱歌水平要比小乐高，你同意吗？

?

2.集中性

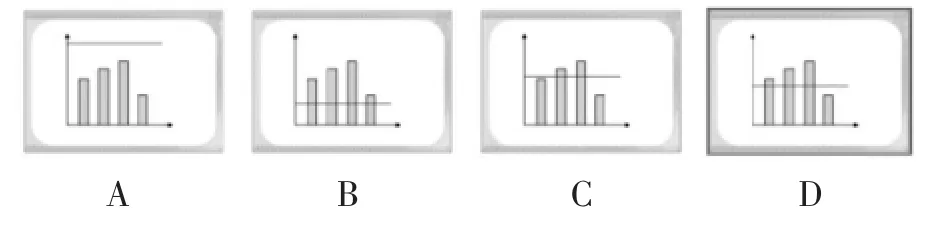
平均数的集中性是指平均数一定介于最大值与最小值之间，理解这点有助于学生理解平均数作为集中量数的原因。那么，如何让学生体会平均数的集中性呢？教师可提供以下材料，并提问：“下图中，哪幅图中的线代表了这组数据的平均水平？”通过问题引导学生根据平均数的意义和“移多补少”的方法进行辨析，明确平均数不会比最大值还大，也不会比最小值还小，因为这不符合平均数的概念。而对选项D，则要通过更加细致的辨析，让学生了解“移多补少”的结果是各个数据均等，从而对平均数有更深入的认识。

3.虚拟性

由于平均数是通过“移多补少”得到的量，因此平均数代表的是这组数据的一般水平，不代表数据中的个体。如图5中，女生队踢毽子的数量为18、13、11个，这组数据的平均数是14，这个14不是任何一个女生踢毽子的数量。

另外，学生没有学过分数除法和小数除法，对平均数是分数（小数）存在着认知障碍，这是正常的现象。如果教师教学时能打破这一障碍，将对学生理解平均数的虚拟性大有裨益。结合图5，教师可以这样向学生设问：“如要使男生队获胜，老师至少踢几个？”这是一个极富挑战性的问题，教师要给足学生思考的时间和交流的机会。教学中，学生提出“老师至少要再多踢8个毽子，这样才能使男生队的平均数达到15个，比女生队的平均数高1个”。有这种想法的学生是需要鼓励的，因为他们有着较强的分析能力，能从问题出发找到答案。

图5　

此时，教师可进一步启发学生：“还有更好的方法吗？”一生提出“只要再多踢5个毽子就行了（如图6）”，此时男生踢毽子的平均数已经达到14个，而且还多出1个。这时有学生质疑：“这多出的1个怎么办？这样是不平均的。”教师可追问：“你有办法将这多出的1个继续平均分吗？”通过问题，引导学生将这1个再平均分成4份。由于学生在学习分数时已经有了类似的经验，所以这时学生发现平均数不是整数了。“那改用一个怎样的数表示呢？”由于学生没有学过带分数和小数，教师可适时介绍：“可以用14或14.25来表示（如图7）。”

图6　

图7　

通过一系列问题的提出与解决，学生茅塞顿开，对平均数的敏感性和虚拟性有了进一步的认识，在解决思维障碍的同时，对所学概念有了更加深刻的印象。

总之，教师应重视概念教学，通过数形结合等途径，引导学生深挖概念的内涵，明晰所学的概念，真正掌握所学的知识。

（责编杜华）

G623.5

A

1007-9068（2016）23-032