有限群的E-可补准素子群

杨　雪，易小兰

(浙江理工大学理学院，杭州 310018)



有限群的E-可补准素子群

杨雪，易小兰

(浙江理工大学理学院，杭州 310018)

运用极小阶反例法，研究E-可补子群对有限群幂零性的影响。在群系中，利用群G的正规子群(Sylow子群)的n-极大子群在G中的E-可补性，得到G为幂零群的一些充要条件，推广和改进了Skiba、李长稳等得出的一些结论。

有限群；s-拟正规；s-拟正规嵌入；E-可补子群；p-幂零

0　引　言

本文中所有的群都是有限群。|G|表示群G的阶，Gp表示G的一Sylowp-子群。Kegel[1]引进了s-拟正规的概念：群G的子群H称为在G中s-拟正规的，如果H与群G的每一个Sylow子群可交换。1996年，Ballester-Bolinches等[2]将s-拟正规子群的概念推广到s-拟正规嵌入中。群G的子群H称为在G中s-拟正规嵌入的，如果对于每一个整除|G|的素数p，H的Sylowp-子群同时也是G的某个s-拟正规子群的Sylowp-子群。2012年，Li[3]提出了E-可补的概念，它包含s-拟正规嵌入同时也包含了Skiba的弱s-可补，得到了有限群结构的一些新结果[4-6]。如文献[3]证明：若E是G的正规子群，如果对于E的每一个非循环Sylow子群P，若P的所有的极大子群或者P的阶为素数或4的循环子群在G中E-可补，则每一个包含在E中的G-主因子是循环的；文献[5]证明：若F是包含所有超可解群的饱和群系，H是G的正规子群且满足G/H∈F，如果对于任意的p∈π(H)(p≠2)，F*(H)的任意非循环Sylowp-子群的所有极大子群在NG(P)中E-可补,且F*(H)的任意Sylow 2-子群的所有极大子群在G中E-可补，则G∈F。

本文进一步了研究子群的E-可补性与有限群的p-幂零性之间的关系，并得到了一些有趣的结论，利用本文的结论，可以直接推导出Skiba、李长稳等提出的一些结果。

1　预备知识

定义[3]群G的子群H称为在G中是E-可补的，如果存在G的一个子群K使G=HK且H∩K≤HeG，其中HeG由包含在H中的G的所有s-拟正规嵌入子群生成。

引理1[3]设H是G的子群，H在G中E-可补。

a)如果K是包含H的G的子群，则H在K中E-可补；

b)如果N是G的正规子群且N包含在H中，则H/N在G/N中E-可补；

c)如果H是G的π-子群,N是G的正规π′-子群，则HN/N在G/N中E-可补。

引理2[7]假设G的子群H在G中有p-幂零补充T。

a)如果N◁G，则HN/N在G/N中有p-幂零补充TN/N；

b)如果H≤L≤G，则H在L中有p-幂零补充T∩L。

引理3[7]设G是一个群，对于某一整数m≥1，素数p满足pn+1|/|G|。如果(|G|,(p-1)(p2-1)…(pn-1))=1，那么G是p-幂零的。

引理4[7]假设H在G中s-拟正规，P是H的Sylowp-子群，其中p为一素数。如果HG=1，则P在G中s-拟正规。

引理5[7]设P是G的s-拟正规p-子群，其中p是|G|的素因子，则NG(P)≥Op(G)。

引理6[3]若p为一素数，G为群满足(|G|,p-1)=1。假设P是G的Sylowp-子群使得P的每一个极大子群在G中有p-幂零补充，则G是p-幂零的。

引理7[8]设F是一个子群闭的饱和群系,H是群G的一个子群，则Z∞(G)∩H≤Z∞(H)。

引理8[9]设P是一个包含在Op(G)中的p-子群，假设P在G中s-拟正规嵌入，则P在G中s-拟正规。

2　主要定理和推论

定理1设G是一个群，p是一素数且对于某个不小于1的整数n，有(|G|,(p-1)(p2-1)…(pn-1))=1。如果G有一个Sylowp-子群P，使得P的每一个在G中没有p-幂零补充的n-极大子群(如果存在)在G中E-可补，则G是p-幂零的。

证明：假设定理1不成立，并设G为极小阶反例。由引理3知，pn+1||G|，由引理6知，P存在极大子群P1使得P1在G中没有p-幂零补充，故存在P的非单位n-极大子群Pn使得Pn在G中没有p-幂零补充。因此，由假设G有一个非p-幂零子群T使得G=PnT且Pn∩T=(Pn)eG。

a)G不是非交换单群。假设G为非交换单群，如果(Pn)eG=1，则|T|p=pn。由引理3知，T为p-幂零，矛盾。故假设(Pn)eG≠1，令U1,U2,…,Us是Pn的所有在G中s-拟正规嵌入的非单位子群。因此，对于每一个i∈{1,2,…,s}，存在G的s-拟正规子群Ki使得Ui是Ki的Sylowp-子群。通过假设得(Ki)G=1，由引理4知，Ui是G的s-拟正规子群。Ui,Ki均为G的s-拟正规子群，故可得Ui◁◁G,Ki◁◁G，从而得到1≤Ui◁◁Ki◁◁G，矛盾。

b)Op′(G)=1. 假设Op′(G)≠1，因P是G的Sylowp-子群，所以POp′(G)/Op′(G)是G/Op′(G)的Sylowp-子群。令M/Op′(G)是POp′(G)/Op′(G)的n-极大子群，则M=PnOp′(G)，其中Pn为P的n-极大子群。如果Pn在G中有p-幂零补充K，则由引理2a)有M/Op′(G)在G/Op′(G)中有p-幂零补充KOp′(G)/Op′(G)。如果Pn在G中E-可补，则由引理1 c)有M/Op′(G)在G/Op′(G)中E-可补。因此，G/Op′(G)满足定理1的所有条件。由G的极小性得G/Op′(G)是p-幂零的，故G是p-幂零的。

c)Op(G)≠1. 假设Op(G)=1，本文分两种情况讨论：如果(Ki)G=1，由a)知Ui是G的s-拟正规子群，故有(Pn)eG在G中s-拟正规，可知(Pn)eG次正规于G，故Pn∩T≤(Pn)eG≤Op′(G)=1，有|T|p=pn，由引理3知，T是p-幂零的，矛盾。如果(Ki)G≠1，则(Ki)G◁Op′(G)，与b)Op′(G)=1矛盾。

d)G/L是p-幂零的，对于包含在Op(G)中的G的任意正规子群L。如果|G/L|≤pn，则由引理3可知G/L是p-幂零群。故假设|G/L|≥pn+1。令Mn/L是P/L的任意n-极大子群，显然易得Mn=Pn。又Pn在G中E-可补，由引理1a)，Mn/L在G/L中E-可补。由G的极小性得G/L是p-幂零的。

e)N=Op(G)是包含在Op(G)中的G的唯一的极小正规子群，对于G的某极大子群M有G=NM且M是p-幂零的。设N是包含在Op(G)中的G的极小正规子群，显然，N是初等交换p-群，N是包含在Op(G)中的G的唯一的极小正规子群且NΦ(G)。因此，存在G的极大子群M使得G=NM，从而M≅G/N是p-幂零的且Op(G)=Op(G)∩NM=N(Op(G)∩M)。因为N≤Op(G)≤F(G)≤CG(N)，所以Op(G)∩M在G中正规，从而Op(G)∩M=1，于是N=Op(G)。

f)P的每一个n-极大子群在G中有p-幂零补充。令Pn是P的任意n-极大子群，可得Pn在G中有p-幂零补充。否则，Pn在G中E-可补，故存在G的一个非幂零子群T使得G=PnT且Pn∩T=(Pn)eG。如果(Pn)eG=1，则|T|p=pn。由引理3知，T是p-幂零的，矛盾。故假设(Pn)eG≠1，令U1,U2,…,Us是Pn的所有在G中s-拟正规嵌入的非单位子群。因此，对于每一个i∈{1,2,…,s}，存在G的s-拟正规子群Ki使得Ui是Ki的Sylowp-子群。假设对于某个i∈{1,2,…,s}，有(Ki)G≠1，故由e)，N≤(Ki)G≤Ki，从而N≤Ui≤Pn且G=NM=PnM，这说明Pn在G中有p-幂零补充M，矛盾。因此，对于每一个i∈{1,2,…,s}，有(Ki)G=1。由引理4知，Ui在G中s-拟正规，因此，(Pn)eG在G中s-拟正规。由引理5，有NG[(Pn)eG]≥Op(G)。因(Pn)eG次正规于G，故有Pn∩T≤(Pn)eG≤Op(G)=N，进一步得(Pn)eG≤Pn∩N且1<(Pn)eG≤((Pn)eG)G=((Pn)eG)Op(G)P≤(Pn∩N)P=Pn∩N≤N。从而得((Pn)eG)G=Pn∩N=N，故N≤Pn，所以Pn在G中有p-幂零补充M，矛盾。

g) 最后的矛盾。由 d)，P的每一个极大子群在G中有p-幂零补充，由引理6，G是p-幂零群，矛盾，这表明极小反例不存在，定理结论成立。

定理2设G是一个群，p是一素数且对于某个不小于1的整数n，有(|G|,(p-1)(p2-1)…(pn-1))=1，F是包含所有p-幂零群的饱和群系。则G∈F，当且仅当G有一个正规子群E使得G/E∈F且E有一个Sylowp-子群P使得P的每一个在G中没有p-幂零补充的n-极大子群(如果存在)在G中E-可补。

证明：必要性是显然的，这里仅给出充分性的证明。假设定理充分性不成立，并设G为极小阶反例。由引理1 a)知,P的每一个在G中没有p-幂零补充的n-极大子群在E中是E-可补的。因此由定理1得，E是p-幂零的。显然，E≠G。令T是E的正规Hallp′-子群，则有：

a)T=1，进一步得P=E◁G。假设T≠1，由T是E的正规Hallp′-子群且E◁G，可知T◁G，故可断言G/T(相对于E/T来说)满足定理2的条件。实际上，(G/T)/(E/T)≅G/E∈F且E/T是p-群。令Mn/T是PT/T的一个n-极大子群且Pn=Mn∩P，其中PT/T在G/T中没有p-幂零补充，则Pn是P的n-极大子群且Mn=PnT。由假设，Pn在G中是E-可补。由引理1 a)知，Mn/T=PnT/T在G/T中是E-可补的。由G的极小性，G/T∈F。设fi(i=1,2)是饱和群系函数使得N=LF(f1),F=LF(f2)。因为T是G的正规p′-子群，所以对Ti+1≤T的每个G-主因子Ti+1/Ti和每个整除|Ti+1/Ti|的素数q，有G/CG(Ti+1/Ti)∈f1(q)。由N∈F知，f1(q)⊆f2(q)，得G/CG(Ti+1/Ti)∈f2(q)。又G/T∈F，故G∈F，矛盾。即可知T=1，进一步得到P=E◁G。

b)设Q是G的Sylowq-子群，其中q是整除|G|素数且满足q≠p，则PQ=P×Q。 由 a)知，P=E◁G，故PQ是G的一个子群。由引理1 a)知，P的每个在PQ中没有p-幂零补充的n-极大子群在PQ中E-可补。故由定理1知，PQ是p-幂零的，从而得Q◁PQ，故PQ=P×Q。

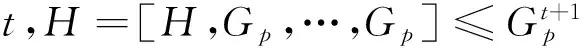
定理3设G是一个群，p是整除|G|的阶的素因子。假设G的每个p阶子群含于Z∞(G)中且G的所有阶为4的循环子群〈x〉在G中E-可补，那么G为p-幂零群。

证明：假设论断不成立，并设G为极小阶反例。则：

a)G的每个真子群是p-幂零的。假设H是G的真子群并设〈x〉是G的p-阶子群。由定理的条件，〈x〉⊆Z∞(G)，又由引理7，〈x〉≤Z∞(G)∩H≤Z∞(H)。令〈x〉是H的四阶循环子群。由假设，〈x〉在G中是E-可补的，则再由引理1 a)知，〈x〉在H中是E-可补的，这样H满足定理的假设。由G的极小性知，H是p-幂零的。

b)G有一个正规Sylowp-子群满足：(i)G=PQ，其中Q是G的Sylowq-子群；(ii)P/Φ(P)是G的主因子；(iii)exp(P)=4或者exp(P)=p。事实上，G是一个极小非p-幂零群。因此，由文献[11]定理8.3.4 b)成立。

c) exp(P)=4. 假设exp(P)=p，则由定理条件，P≤Z∞(G)，从而G/Z∞(G)≅(G/P)/(Z∞(G)/P)是p-幂零的，故G是p-幂零的，矛盾。

d)|x|=4,其中x∈P/Φ(P)。假设存在x∈PΦ(P)使得|x|=2。设T=〈x〉G，则T≤P且TΦ(P)/Φ(P)正规于G/Φ(P)。因为P/Φ(P)是G的主因子，所以P=T，从而exp(P)=2，与c)矛盾。

e)最后的矛盾。令T是〈x〉在G中的任意补充，则G=〈x〉T且P=P∩G=P∩〈x〉T=〈x〉(P∩T)。又P/Φ(P)是交换群，有(P∩T)Φ(P)/Φ(P)◁G/Φ(P)。然而P/Φ(P)是G/Φ(P)的极小正规子群，故P∩T≤Φ(P)或P=P(P∩T)Φ(P)=P∩T。如果P∩T≤Φ(P)，则〈x〉=P◁G，接着由文献[12]定理10.1.9得G是p-幂零的，矛盾。故假设P=P∩T，对任意的补充T，则T=G是〈x〉在G中的唯一的补充。由假设及G的极小性知，T=G不是p-幂零的，故〈x〉在G中E-可补。由引理8得，〈x〉=〈x〉eG在G中s-拟正规的，则〈x〉Q是G的真子群且〈x〉Q=〈x〉×Q，从而得到G=P×Q，矛盾。

推论1设G是一个群，假设G的每一个极小子群含于Z∞(G)中且G的每个四阶循环子群〈x〉在G中E-可补，则G是p-幂零的。

推论2(文献[3] 定理3.2) 设P是G的Sylowp-子群，其中p是整除|G|的最小的素数，如果P的每一个在G中没有p-幂零补充的极大子群在G中E-可补，则G是p-幂零的。

推论3 (文献[4]，定理3.1) 设G是一个群，p是一素数且对于某个不小于1的整数n，有(|G|,(p-1)(p2-1)…(pn-1))=1。如果G有一个Sylowp-子群P使得P的每一个n-极大子群(如果存在)在G中或者存在p-幂零补充，或者弱s-可补，则G是p-幂零的。

推论4(文献[13]，定理) 设G是一个群，p是一素数且对于某个不小于1的整数n，有(|G|,(p-1)(p2-1)…(pn-1))=1。如果G有一个Sylowp-子群P使得P的每一个n-极大子群(如果存在)在G中或者存在p-幂零补充，或者弱s-可补，则G是p-幂零的。

3　结　语

群G的所有正规子群，c-正规子群、c-可补子群、s-置换子群、弱s-可补子群、s-拟正规嵌入子群都是G的E-可补子群。本文主要考虑当有限群的阶满足(|G|,(p-1)(p2-1)…(pn-1))=1时，利用子群的E-可补充性研究有限群的结构和性质，得到有限群为幂零群以及更一般的属于包含所有幂零群的饱和群系的条件。在后续研究中，讨论将定理中群G的阶的条件削弱为(|G|,p-1)=1时，群G的Sylow子群的极大子群的E-可补性与有限群的幂零性的关系。

[1]KEGELOH.Sylow-gruppenandsubnormalteilerendlicherGruppen[J].MathematischeZeitschrift, 1962, 78(2): 205-221.

[2]BALLESTER-BOLINCHESA,PEDRAZA-AGUIERAMC.Sufficientconditionsforsupersolvabilityoffinitegroups[J].JournalPureAppliedAlgebra, 1998, 127(2): 113-118.

[3]LICW.AnoteonaresultofSkiba[J].JGroupTheory, 2012, 15(3):385-396.

[4] 谢凤艳，郭文彬，李宝军. 关于广义置换子群理论中的一些公开问题[J].中国科学:A辑，2009,39(5): 593-604.

[5]ZHANGXM,LICW.FinitegroupswithE-supplementedsubgroups[J].VietnamJournalofMathematics, 2013, 41(3) :333-339.

[6]YIXL,SKIBAAN.OnsomegeneralizationsofpermutabilityandS-permutability[J].ProblemsofPhysics,MathematicsandTechniques, 2013, 17(4):65-78.

[7]LICW.Finitegroupwithsomeprimarysubgroupsss-quasionrmallyembedded[J].IndianJournalPureAppliedMathematics, 2011, 42 (5):291-306.

[8]GUOWB.OnF-supplementedsubgroupsoffinitegroups[J].Manuscriptamathematica, 2008, 127(2): 139-150.

[9]LIYW,WANGYM,WEIHQ.Onp-nilpotencyoffinitegroupswithsomesubgroupsπ-quasinormallyembedded[J].ActaMathematicaHungarica, 2005, 108(4): 283-298.

[10]DOERKK,HAWKEST.Finitesolublegroups[M].WalterdeGruyter,Berlin,NewYork, 1992:99-107.

[11] 徐明耀. 有限群导引：下[M]. 北京：科学出版社，1993: 20-38.

[12]ROBINSONJSD.Acourseintheoryofgroups[M].NewYork:Springer,1995:53-82.

[13] 李长稳, 易小兰. 关于s-拟正规嵌入子群[J]. 佛山科学技术学院学报: 自然科学版, 2012, 30(3): 19-22.

(责任编辑： 康锋)

Some Primary SubgroupsE-supplemented of Finite Group

YANGXue,YIXiaolan

(School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The authors investigated the influence ofE-supplemented subgroups on nilpotency of finite groups by using the method of minimal order counterexample. A series of necessary and sufficient conditions for a group to be nilpotent are obtained in formation by means of some groups ofG, such asn-the maxmal subgroups of the normal subgroup ofG,n-maxmal subgroups of the Sylow subgroup ofG,etc. Some of Skiba and Changwen Li’s results are generalized and improved.

finite group;s-quasi-normality;s-quasi-normalE-embedding;supplemente subgroup;p-nilpotency

10.3969/j.issn.1673-3851.2016.03.026

2015-5-18

国家自然科学基金项目(11471055)

杨雪(1990-)，女，湖北荆门人，硕士研究生，主要从事代数学方面的研究。

O152.1

A

1673- 3851 (2016) 02- 0313- 04 引用页码： 030802