应用Matlab软件图形处理功能辅助微积分概念教学探讨*

张美恋

(集美大学理学院，福建 厦门 361021)



应用Matlab软件图形处理功能辅助微积分概念教学探讨*

张美恋

(集美大学理学院，福建 厦门 361021)

针对学生理解比较困难的微积分中的极限、导数、定积分等概念，应用Matlab软件图形处理功能，通过典型的例子，动态地显示理解这些概念的思想方法，从几何方面直观地帮助学生理解相关的概念，从而提高学生的学习兴趣，进而提高教学效果.

微积分；概念教学；Matlab软件； 图形;辅助教学

引言

高等数学是大学理工类、经管类院校学生必修的一门重要的公共基础课程，而微积分是高等数学的核心内容，同时高等数学也是学生普遍反映比较困难的课程之一.笔者在多年的教学实践中发现，成绩不理想很重要的原因之一是大部分学生在概念的理解上出现困难，而在高等数学学习过程中，像极限、导数、定积分等基本概念比较抽象，学起来普遍觉得困难. 但这些概念是微积分的精髓所在，同时也是后续课程应用最为频繁的知识点. 如何准确理解掌握这些基本概念是学好高等数学的关键. 本文针对学生在高等数学学习过程中遇到的困难，应用Matlab软件图形处理功能，尽可能形象地把抽象的数学定义用图形动画等形象进行演绎，给学生有一些直观的认识，这将大大加深学生对这些概念的理解，同时有助于学生了解这些基本概念的逻辑形态和算法形态，有助于提高学生的学习兴趣.

1　Matlab软件对极限概念的辅助教学

极限是微积分最重要的概念之一，它贯穿于微积分教学的整个过程，是研究微积分的主要工具. 函数是变量的变化关系最基本的数学描述，它是微积分研究的主要对象，而极限揭示了变量在一定的变化过程中的终极状态，微积分的很多概念，例如连续、导数、积分都是建立在极限定义的基础上.传统的“ε-δ”定义，对于非数学专业的学生来讲是有一定困难的，本文结合例子用Matlab的绘图功能数列极限描述性定义及函数极限描述性定义进行辅助教学.

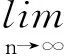
n=1:80;

plot(n,(1+1./n).^n,'.')

holdon

gridon

ylim([2,3])

实现在图形上直接地观察出数列的极限,运行结果如图1所示.

图n数列的图像

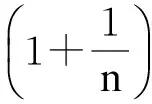
自变量趋于有限值时函数极限的描述性定义[1]：

自变量趋于无穷大时函数极限的描述性定义：

symsx

fplot(inline(sin(x)/x),[-10*pi,10*pi])

holdon

gridon

ylim([-0.4,1.2])

实现在图形上直接地观察出函数在不同趋势下的极限,如图2所示.

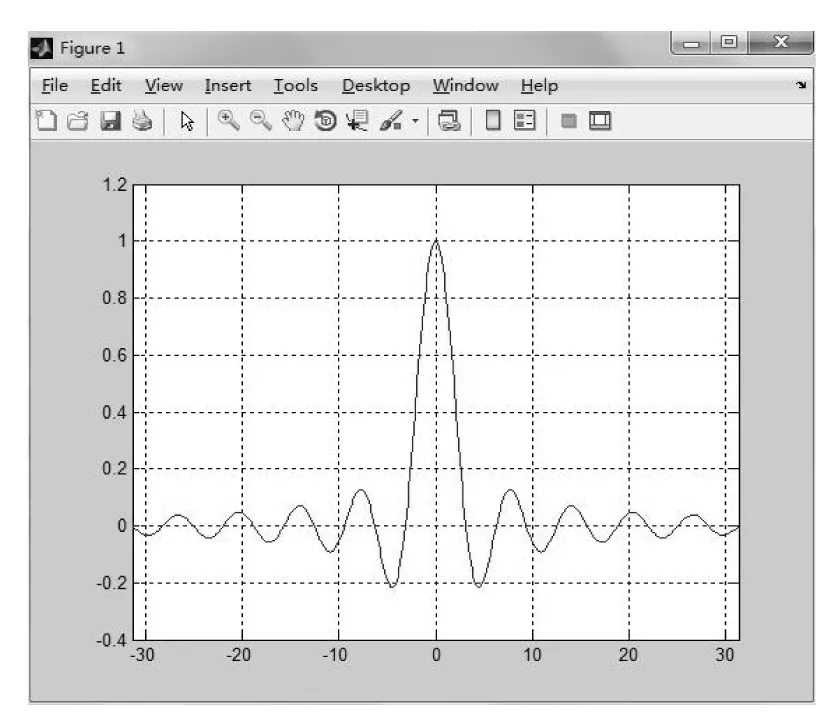
图函数的图像

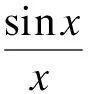
2　Matlab软件对导数概念的辅助教学

微分学是微积分的重要组成部分，它的基本概念是导数与微分. 导数是建立在函数极限的基础之上的，导数的概念在于刻划瞬时变化率问题.

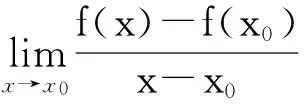
symsx

fun=3+2*x-x^2;

f1=inline(diff(fun));

f2=f1(0)*x+3;

fplot(inline(f2),[-1,3])

holdon

fplot(inline(fun),[-1,3])

holdon

k=0.2:0.2:1.8;

f3=inline(fun);

f4=3+((f3(k)-f3(0))./k)*x;

fplot(inline(f4),[-1,3],'k')

holdon

ylim([1,5])

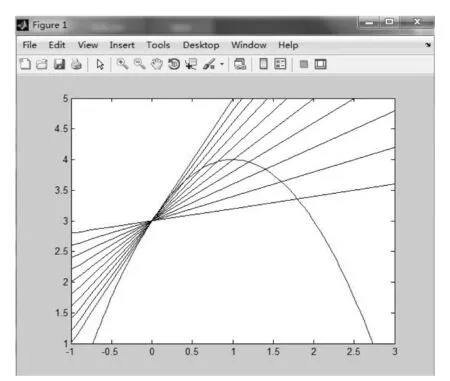
图3　f(x)=3+2x-x2的割线与切线

通过观察图形3可以发现，割线通过固定点(0,3)，它经过的另一点是曲线上的动点，当动点沿曲线靠近定点时，割线越来越靠近切线，切线y=2x+3是割线的极限位置，切线的斜率2就是函数f(x)在x0=0处的导数.

3　Matlab软件对定积分概念的辅助教学

积分学是微积分的另一个重要组成部分，它的基本概念是定积分. 定积分是建立在函数极限的基础之上的，定积分在于刻划连续变量的“累加”问题，根据定积分的定义，连续函数在某一闭区间上的定积分等于该区间上划分的最大长度趋于零时黎曼和的极限值. 大部分高等数学教材中的定积分定义，是通过分析曲边梯形的面积的求解步骤引出的. 曲边梯形面积的求解由“分割，近似替代，求和，取极限”四个步骤完成，以求曲线f(x)=sinx及x=0,x=π和x轴所围成的曲边梯形面积为例，应用以下语句实现上述四个步骤[3]，并用图形进行演示(图4～9).

a=0;b=pi;

m=[10,20,50,100,200,500];

n=length(m);

for j=1:n

h=(b-a)/m(j);

g=sin(a+h*rand);

for i=1:m(j)-1

y=sin(a+i*h+rand*h);

g=[g;y];

end

x=a:(b-a)/100:b;

plot(x,sin(x),'r')

axis([a,b,sin(a),sin(pi/2)])

grid on

hold on

x2=a+0.5*h:h:b-0.5*h;

bar(x2,g,1.0,'c')

pause(10)

hold off

end

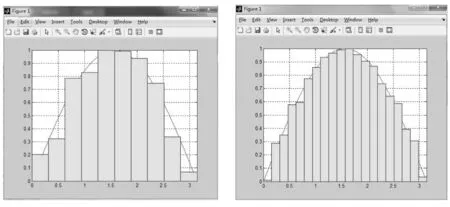
图4　m=10的黎曼和　　　　　　　　　　　　 图5　m=20的黎曼和

图6　m=50的黎曼和　　　　　　　　　　　　　 图7　m=100的黎曼和

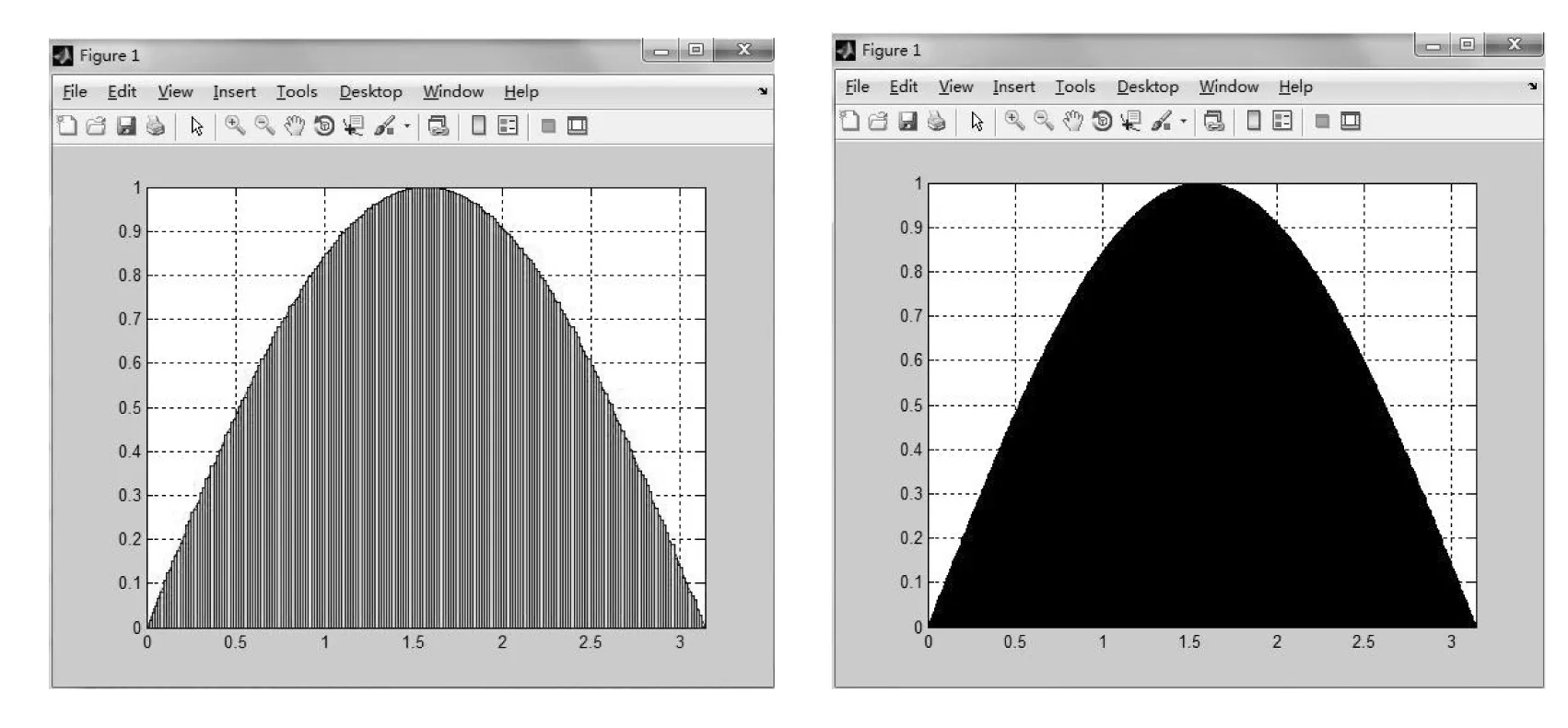
图8　m=200的黎曼和　　　　　　　　　　　　　　　 图9　m=500的黎曼和

4　结语

在教学过程中，本文针对多数学生理解比较困难的微积分中的一些重要概念，如极限、导数、定积分等，利用Matlab软件图形处理功能，通过典型的例子，动态地显示这些概念的思想方法，从几何方面直观的帮助学生理解相关的概念. 这种将数学软件融入教学中辅助概念的教学，有利于学生更容易掌握数学思想和方法，在这基础上，引导学生将这些思想方法运用于解决实际问题. 随着数学软件的层出不穷，多元化的教学更是一种趋势，这就对教师提出了更高的要求. 教师不但要能讲授知识，而且要会应用数学软件不断改进教学方法，以适应新时期对人才培养的要求.

[1]上海交通大学，集美大学.高等数学——及其教学软件(上册)[M].北京：科学出版社，2010.

[2]占海明.基于MATLAB 的高等数学问题求解[M]. 北京：清华大学出版社，2013.

[3]刘广会，曹修文，齐化富.基于Matlab的图形和动画技术在高等数学教学中的应用[J]. 甘肃联合大学学报,2013,27(3):83-86.

Discussion on the Application of Matlab Software Graphics Processing Function on Calculus Concept Teaching

ZHANG Mei-lian

(Science College，Jimei University，Xiamen Fujian 361021, China )

Considering the difficult concepts of the limit, derivative and definite integral of the calculus, this article uses Matlab graphics processing functions, through typical examples, dynamically displays the ways of understanding these concepts, and helps students understand the related concepts from the geometric intuitive view so as to improve their interests in learning and improve the teaching effect.

calculus; concept teaching; supplementary teaching; chart; Matlab software

1673-2103(2016)02-0091-04

2016-03-21

张美恋(1966-)，女，福建东山人，副教授，研究方向：多属性决策，优化理论与应用.

O13

A