一种适合FPGA实现的时频谱图增强算法

陶中幸，王全州，裴　东，杨鸿武

(西北师范大学物理与电子工程学院，甘肃兰州　730070)



一种适合FPGA实现的时频谱图增强算法

陶中幸，王全州，裴东，杨鸿武

(西北师范大学物理与电子工程学院，甘肃兰州730070)

在基于FPGA的时频分析研究设计中，针对直接显示的时频谱图无法体现频谱细节变化的问题，提出了一种适合硬件实现的谱图增强算法.该算法以正弦信号的频谱结构为原型，选用反比例函数逼近正弦信号的频谱包络，并结合实际应用情况推导出具体的增强算法，利用该算法不仅对时频谱图的灰度级进行了压缩，而且进行了谱图增强处理.实验结果表明，此算法可有效显示出时频谱图的细节变化，与对数变换相比，具有运算量小，实时性好，适合硬件实现等特点.

现场可编程门阵列；时频谱图；短时傅里叶变换；图像增强；反比例函数

时频分析是一种处理非平稳信号的重要方法，广泛应用于机械、医学、数学、物理等领域.时频分析的结果通常采用二维图像进行显示，称为时频谱图，其横坐标表示时间，纵坐标表示频率，具体反映了不同时刻的信号频谱变换情况，是一种典型的灰度图像，其中，像素点的灰度值大小表示在该时刻、该频率处的频谱幅值[1-3].在显示时通常采用彩色图像，以增强人眼对图像的敏感度[4-5].时频谱图具有数据动态范围较大，大多数像素灰度值偏小，只有少数像素灰度值偏大等特点，若直接对其进行存储，存储器位宽必须要达到最大灰度值的数据位宽，这就需要消耗大量的存储器资源.若采用截取高位，放弃低位的方法进行数据位宽的压缩，将会改变图像的原始灰度分布情况[5-6]，很多偏小的数据就会丢失，而这部分数据恰巧是时频谱图中最为重要的有用信息.因此，需要找到一种合理的映射关系对图像的灰度进行处理，以降低灰度数据的位宽，且能够对原图像进行增强，使得显示出来的图像具有更多的视觉细节信息.在基于FPGA的时频分析系统中，对非平稳信号做时频分析得到时频谱图，谱图灰度分辨率为65 536级，相比灰度图像常用的256级分辨率来讲属于高分辨率图像，为减小片内存储器的开销，需要将高灰度分辨率图像进行分辨率压缩处理.为此提出一种适合FPGA实现的时频谱图增强算法，实现对图像的灰度分辨率的降低和对原图像的增强处理.

1　问题分析

1.1时频谱图的产生

目前，主要的时频分析方法有短时傅立叶变换(STFT)、S变换(ST)、小波变换(WT)、Wigner-Ville分布(WVD)、Cohen类时频分布等.短时傅里叶变换是得到时频谱图最常用的方法，也叫做窗口傅里叶变换.离散信号x(n)的短时傅里叶变换定义为[7]141

(1)

其中，w(n)是一个可以沿时间方向轴滑动的窗，它的宽度是有限的;STFTx(n,ω)为短时段fn(m)=x(m)w(n-m)的傅里叶变换.

1.2时频谱图特点

图1是对一段语音信号进行时频分析的结果及其直方图，可见，灰度值较大(白色部分)的像素点很少，灰度值较小(黑色部分)的像素点很多.这是由于图像的灰度动态范围过大，在显示时只能显示出灰度值较大的像素点，灰度值较小的像素点显示不出来，或者人眼无法分辨.时频谱图主要分析信号频谱随时间变化的情况，而这部分重要信息都蕴含在大量的灰度值较小的像素点中.

1.3需要解决的问题

为得到比较客观的谱图信息和减小硬件实现过程中的存储器开销，需要对谱图进行增强处理，同时尽可能压缩图像灰度级.对数变换就是一种可选方案，但对数变换在硬件实现中存在很多问题.较为精确的对数求解可选用CORDIC算法[8-9]，它用迭代模式计算多种超越函数算法，选择适当的工作模式可实现对数求解.在系统实现过程中，为协调核心算法处理时序和VGA显示时序，且考虑到FPGA片内存储资源有限，没有选用这一算法，这就需要设计一种能够达到灰度级压缩和谱图增强两种功能的算法.

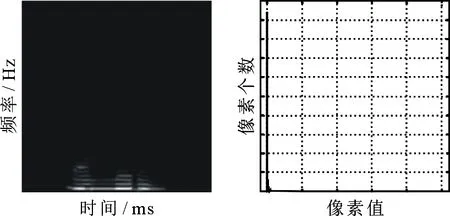
图1　时频谱图特点Fig 1Time-frequency spectrogram features

2　新的增强算法

由傅里叶变换可知，当满足一定的条件时，任意信号可以表示为正弦信号或者它们积分的线性组合，那么就可以假设这一信号的频谱可以由多个正弦信号或者它们积分的频谱组合而成.文中正是在这种思路下以正弦信号的频谱结构为原型，寻找一种能够逼近正弦信号的频谱包络的函数曲线，再结合具体应用情况，推导出新的时频谱图增强算法.

2.1正弦信号的谱结构

通常情况下，对正弦信号做傅里叶变换后得到的信号的频谱如图2所示.可以看出，信号的频谱在整个频率轴上大部分是趋于零值的，而只有几个频率点上的数据偏大，且频谱数值相差很大，具有较大的数据动态范围.采用短时傅里叶变换处理非平稳信号时，得到的结果就是多个信号频谱的依次存储，也应该具有上述信号频谱的特点，因此，对于时频谱图的增强算法可借助正弦信号的频谱结构特点设计.

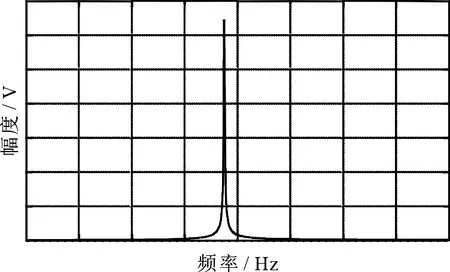
图2　正弦信号的频谱结构Fig 2Spectrum structure of sinusoidal signal

2.2逼近函数选择

根据信号的傅里叶频谱结构，图3中3种函数曲线经过简单的变换都能够满足条件.

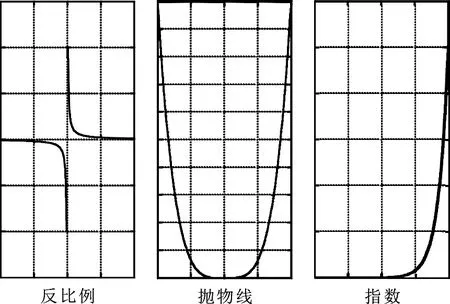
图3　3种逼近函数Fig 3Three different approximation functions

3种函数都可以采用各种变换形式加以应用，如对反比例函数和抛物线函数只取一半，再根据具体问题，适当的加以修正即可.文中对反比例函数进行了具体的修正，以此来设计时频谱图的增强算法.当然也可以采用抛物线函数和指数函数设计时频谱图的增强算法.采用指数函数设计的增强算法，实际上就是图像灰度变换中常见的对数变换算法[10].

2.3新的增强算法

时频谱图具有很大的数据动态范围，增强算法的主要目的就是将时频谱图的数据动态范围进行压缩.图4中的带星号曲线表示正弦信号的频谱，带圆圈曲线是修正的反比例函数对频谱包络的逼近，带三角直线表示线性方式对正弦信号频谱包络的逼近.由图4可见，修正的反比例函数能够很好地逼近信号的频谱包络.

设原图像为f(x,y)，经过增强处理后的新图像为g(x,y)，且假定f(x,y)和g(x,y)的灰度值均为正整数，那么灰度变换可由反比例函数变换而来:

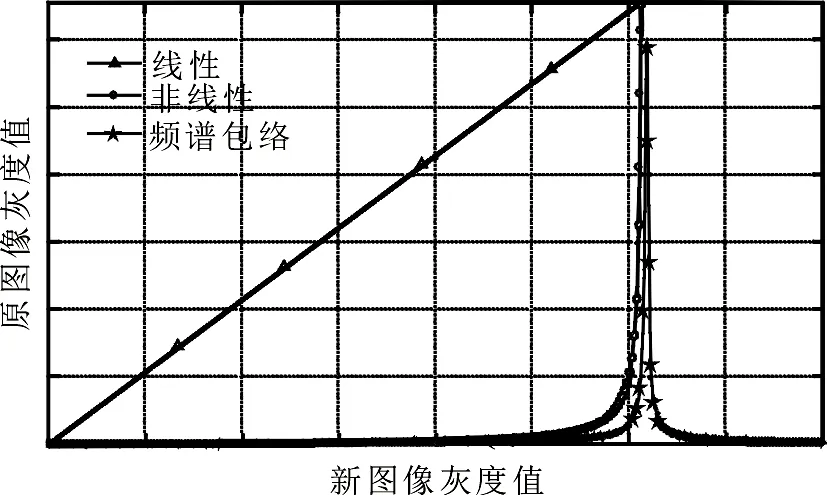
图4　新的增强算法Fig 4New enhancement algorithm

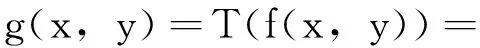
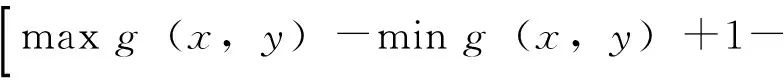
(2)

通常有ming(x,y)=0, minf(x,y)=0,故

(3)

计算(3)式，只需要5个加法器和1个除法器.在FPGA中加法器容易实现，除法器可以由嵌入式乘法器实现.

3　算法仿真实现

3.1与对数变换比较

为了更进一步分析文中提出的增强算法，分别对图像频谱和时频谱图进行文中算法和对数方法增强.图5是文中算法与对数变换的对比图，可以看出，文中算法和对数变换一样，均可以实现图像的增强和灰度级的压缩.另外，与对数变换相比，文中算法在灰度值偏大时分辨能力不足，易造成灰度较大像素点的信息损失.

图5　对数变换与文中算法对比Fig 5Comparison of this paper algorithm with logarithm

3.2时频谱图的增强

对图1所示时频谱图利用文中算法进行处理，得到图6.可见，与图1中的直接显示相比，视觉细节信息更加丰富，谱图得到了显著增强.

3.3硬件仿真

实验中对一段语音信号做时频分析，FPGA平台选用EP2S180F1020C3，分析结果采用VGA方式显示.图7(a)是时频谱图直接显示的结果，显然只能显示谱图中的最大值，大量的含有谱图纹理细节变化信息的像素点因灰度值过小而无法显示出来.图7(b)是利用文中算法对时频谱图进行增强处理的结果，可以很清晰地看到谱图的纹理等细节的变化情况，越白部分表示频谱幅值越大，越黑则表示频谱幅值越小，能够很好地反映出信号频谱随时间变化的细节信息.

图6　时频谱图文中算法增强Fig 6　Enhancement of time-frequency spectrogram with this algorithm

(a)直接显示时频谱图

(b)文中算法增强结果 图7　增强算法FPGA硬件仿真Fig 7Algorithm implementation with FPGA

[1]邹红星，周小波，李衍达.时频分析:回溯与前瞻[J].电子学报，2000，28(9)：78.

[2]李振春，刁瑞，韩文功，等.线性时频分析方法综述[J].勘探地球物理进展，2010，33(4)：239.

[3]佟德纯，姚宝恒.工程信号处理与设备诊断[M].北京：科学出版社,2008.

[4]陶中幸，裴东，王全州，等.基于现场可编程门阵列的语谱图显示与增强[J].计算机应用，2011，31(7)：1995.

[5]刘维，刘纪元，黄海宁，等.声纳图像伪彩色处理的调色板连续色编码方法[J].系统仿真学报，2005，17(7)：1724.

[6]曹茂永，郁道银.高灰度分辨率图像的伪彩色编码[J].光学技术，2002，28(2)：115.

[7]WILLISTON K，GENTILE R，JACK K，et al.DigitalSignalProcessingWorldClassDesigns[M].Oxford：Newnespress，Elsevier，2009.

[8]牟胜梅，李兆刚.一种面向FPGA的指对数函数求值算法[J].计算机工程与应用，2011，47(33)：59.

[9]孙桂玲，纪永鑫，张潺潺.高速高精度FFT IP核的设计与仿真研究[J].系统仿真学报，2010，22(8)：2018.

[10]GONZALEZ R C，WOODS R E.数字图像处理[M].第3版.阮秋琦，阮宇智，译.北京：电子工业出版社，2011.

(责任编辑惠松骐)

A enhancement algorithm of time-frequency spectrogram for FPGA realization

TAO Zhong-xing，WANG Quan-zhou，PEI Dong，YANG Hong-wu

(College of Physics and Electronic Engineering，Northwest Normal University，Lanzhou 730070，Gansu，China)

During the research and design of time-frequency analysis based on FPGA，the direct indication of the time-frequency spectrogram is not able to reflect the variation of spectrum in detail.To solve this problem，an image enhancement algorithm of time-frequency spectrogram based on FPGA is presented in this paper.The algorithm takes sinusoidal signal spectrum structure as design prototype，chooses the inverse proportion function to approximate the spectral envelope of sinusoidal signal，combines with the practical application to derive the specific enhancement algorithms.The algorithm can not only compress the gray level of time-frequency spectrogram，but also enhance the image.Experimental results show that more detail variation of time-frequency spectrogram can be obtained by the algorithm effectively.Algorithm in this paper has the characteristics of much less computation，strong real-time property and suitable for hardware implementation compared with logarithmic transform.

field programmable gate array；time-frequency spectrogram；short-time fourier transform；image enhancement；inverse proportional function

10.16783/j.cnki.nwnuz.2016.03.011

2015-03-19;修改稿收到日期:2015-10-21

西北师范大学青年教师科研能力提升计划资助项目(NWNU-LKQN-14-21)

陶中幸(1986—)，男，甘肃白银人，助教，硕士.主要研究方向为信号处理.

E-mail:newwaves@163.com

TP 391

A

1001-988Ⅹ(2016)03-0057-04