小孔节流器出口圆角对空气静压止推轴承性能的影响*

李　祥　王　杰　阳　红　崔海龙　方　辉

(① 四川大学制造科学与工程学院,四川 成都 610065;②中国工程物理研究院机械制造工艺研究所，四川 绵阳 621900)



小孔节流器出口圆角对空气静压止推轴承性能的影响*

李祥①王杰①阳红②崔海龙②方辉①

(① 四川大学制造科学与工程学院,四川 成都 610065;②中国工程物理研究院机械制造工艺研究所，四川 绵阳 621900)

以小孔节流空气静压止推轴承为研究对象，求解出轴承气膜间隙内的压力与速度分布，分析了节流孔出口处圆角值不同对轴承性能的影响。结果表明：当气膜间隙不变时，在一定范围内，节流孔出口圆角半径值越大，轴承承载力越大，流场中最高流速越低；节流孔出口圆角半径值过大，流场中会出现气旋，降低轴承的稳定性。

气体静压轴承；小孔节流器；气膜；承载力；气旋

静压空气润滑轴承利用气膜支承载荷，是一种理想的支承元件。由于气膜的均化作用以及其极小的摩擦因数，与滚动轴承及油润滑滑动轴承相比,气体轴承具有速度高、精度高、功耗低和寿命长等诸多优点[1-2]。近几年来在机床行业、高速和精密机械工业、医疗器械工业等领域应用广泛[3]。

小孔节流作为空气静压轴承的典型节流方式得到了较多的应用。由于空气静压轴承存在承载力低和稳定性较差的问题，如何提高其承载力和稳定性成为人们关注的重点[4-5]。目前有学者[6-7]分析了小孔节流静压气体轴承内气体的流动特性，并证明漩涡是导致静压气体轴承产生自激振动的直接原因。文献[8]通过实验验证了两种不同气腔结构的小孔节流静压气体轴承的振动特性，分别为节流孔与气腔之间采用直角连接(S-Type)和圆角连接(R-Type)。实验结果表明R-Type比S-Type轴承振动小，但并未研究它的承载力等性能与圆角半径值的关系。

本文以单个小孔节流的止推轴承为研究对象，节流孔出口采用圆角连接结构，运用计算流体力学分析软件 FLUENT[9]建立轴承中流体的模型。通过流场分析，研究节流孔出口圆角值改变，对轴承承载力和稳定性的影响。

1　静压气体止推轴承的建模

1.1数学模型

静压止推轴承内空气满足控制空气流动的Reynolds方程式，即气膜压力分布的数学模型[10]为：

(1)

式中:h为气膜厚度;p为气膜压力；vxh为气膜空气沿x方向速度分量在z坐标为h时的速度边界值;vyh为气膜区空气沿y方向速度分量在z坐标为h时的速度边界值。

气体润滑的主要特征表现为气体的可压缩性,式(1)是气体轴承性能计算的基本方程,此非线性偏微分方程很难用数学方法求得解析解[11]。

1.2几何模型

单孔止推轴承的结构示意图如图1，图中结构参数：L为节流小孔深度，d为直径，h为气膜厚度，R为小孔出口圆角半径。

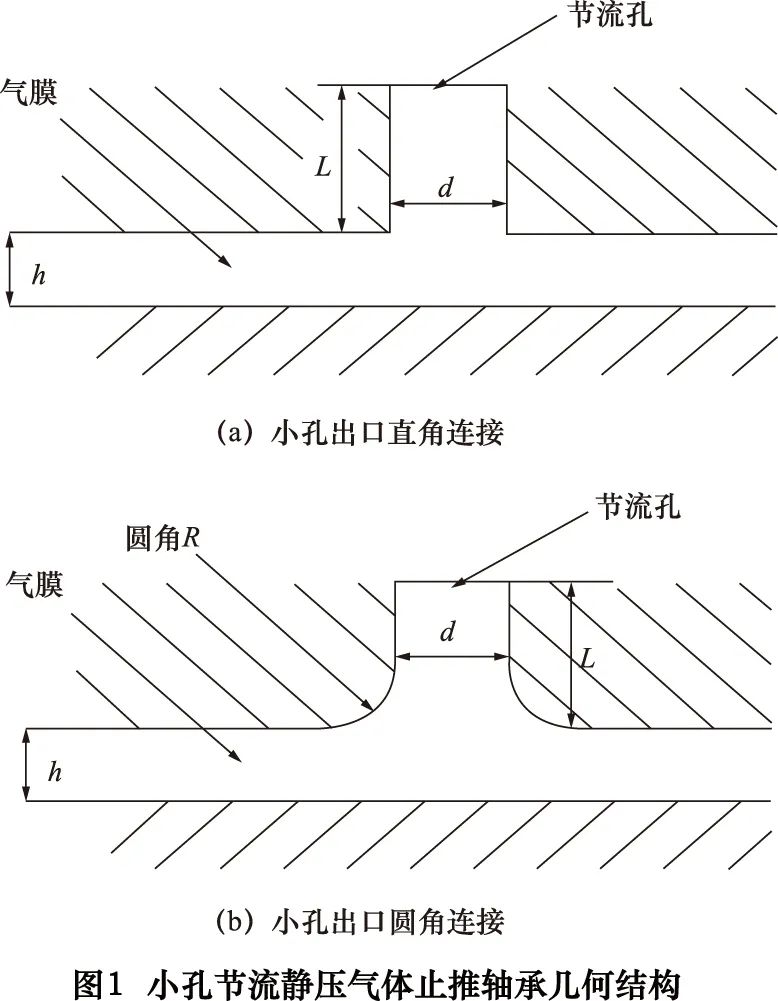
2　仿真计算与结果讨论

2.1计算流体力学模型及边界条件

建模时，主要考虑空气在节流小孔以及气膜中的流动。根据轴承的对称性，简化为二维轴对称模型，可以减小计算量，并提高计算速度。利用Geometry模块建立模型并在Mesh中完成网格的划分，整个流体区域采用四边形结构网格划分，节流孔出口附近气体流速与压力变化迅速，采用致密的网格以提高计算精度;划分后的网格如图2所示。

将Mesh 中生成的空气静压止推轴承流场网格模型导入 FLUENT 中，分析气膜压力分布情况、流场速度以及气膜承载力。求解器设置选用基于压力的求解器(pressure based)，空间设置为轴对称，模型采用标准k-ε湍流模型，材料为理想空气。边界条件设置：进口压力为0.5 MPa，出口压力为0 Pa(即环境压力)，压力速度耦合算法设置为 SIMPLIC 算法。

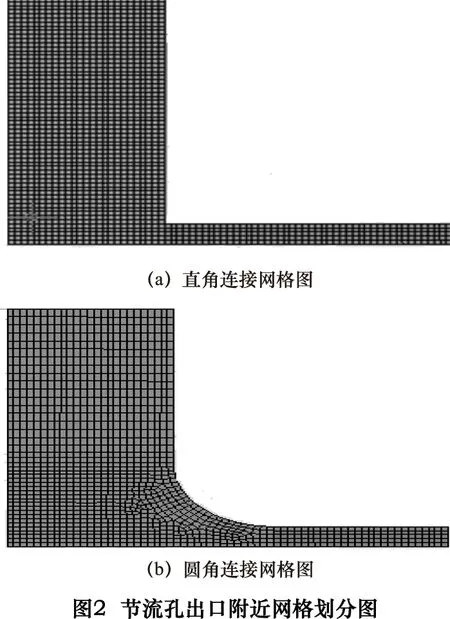
2.2仿真结果分析

选取空气静压止推轴承的直径D=50 mm，节流孔深度L=0.3 mm，节流孔直径d=0.1 mm，气膜厚度h=10 μm，节流孔出口圆角半径从0～100 μm变化，分析其对空气静压止推轴承性能的影响。

2.2.1节流孔出口圆角对压力场的影响

通过 ANSYS FLUENT 模块对轴承流场进行流体分析，可以获得气膜内每个节点的压力，从而可以计算出整个气膜的承载力。图3为直角连接和圆角(R=5 μm)连接节流孔附近压力分布图。从图中可看出，空气以供气压力进入节流孔后气体压力基本未发生改变; 当空气从节流孔流入轴与轴承之间的缝隙时，首先出现压力突降，然后沿着半径方向有所上升，之后又逐渐降低至环境压力。对比图 3a和图3b可知，采用圆角连接时，气膜内的压力分布更均匀，平均压力值也较大。

对于不同圆角半径，轴承底面半径方向上的压力分布如图 4 所示。由图4可知，对于直角连接(R=0 μm)节流器，供气孔处压力从0.5 MPa陡降到了0.12 MPa，然后略有回升后平稳降低。虽然均存在压力突降现象，但圆角连接的压力下降幅度明显小于直角连接，随着圆角半径的增加，压力下降越平缓，平均压力也越大；由于气膜起直接承载作用，所以其平均压力越大，越有利于提高轴承承载力。

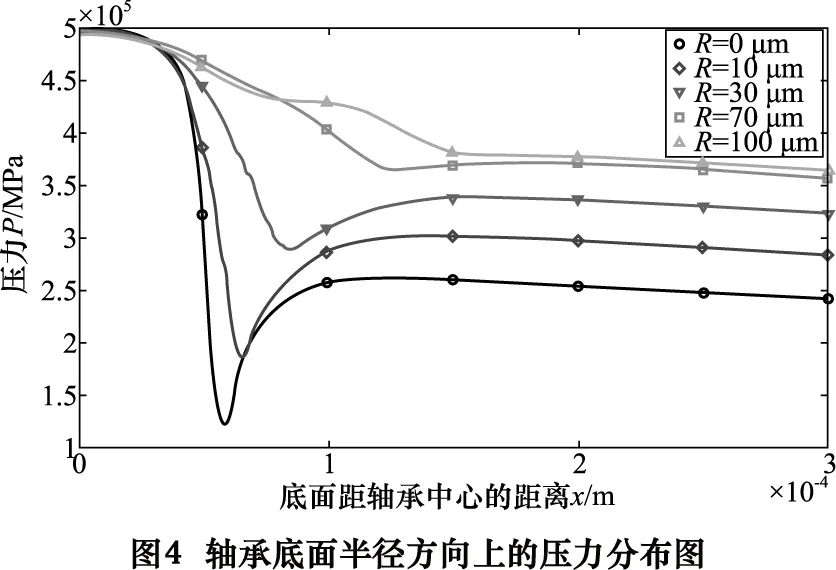
2.2.2节流孔出口圆角对承载力的影响

图5为轴承在两种工作气膜间隙(h=10.20 μm)下,不同圆角半径对应的承载力。由图可以看出，随节流孔出口圆角半径值增大,轴承承载能力增大,这是由于当出口圆角半径增大时,节流孔口对气体的阻力减小,减缓了出口压力突降，增大了气膜内平均压力，从而提高了承载力。当R达到一定值(h=10 μm，R>30 μm;h=20 μm,R>80 μm),继续增大圆角半径,承载力几乎不再上升,这是因为孔口圆角半径值超过一定范围时,节流孔附近气膜的压力接近于小孔出口压力,承载力接近极值，难以再继续增大。

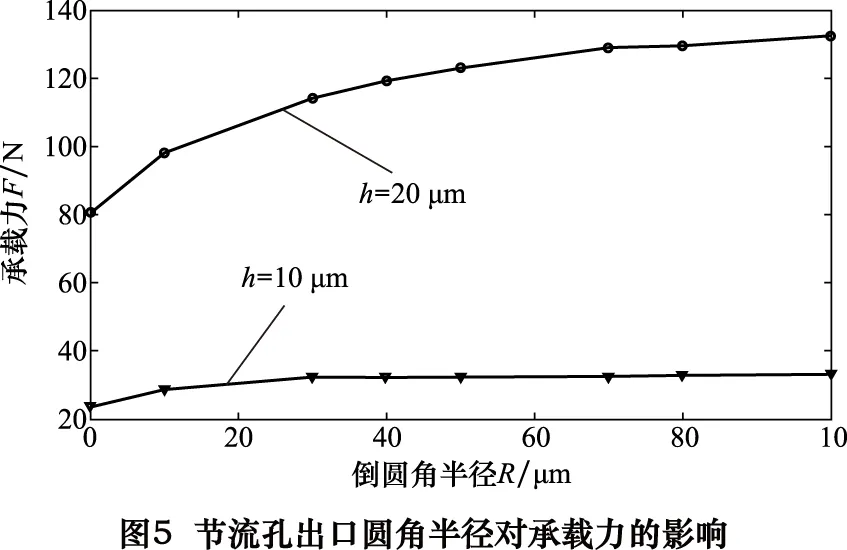
2.2.3节流孔出口圆角对速度场的影响

图6为节流孔附近速度场云图，可以看出，孔口采用圆角连接(R=50 μm)的流场最高流速(209 m/s)明显低于直角连接(R=0 μm)的最高流速(378 m/s)；气体从小孔流入气膜，速度方向会发生急剧变化，节流孔出口处增加圆角，可以起过渡导流作用，减缓出口节流引起的速度突增。

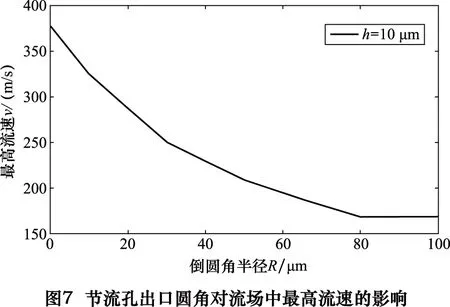
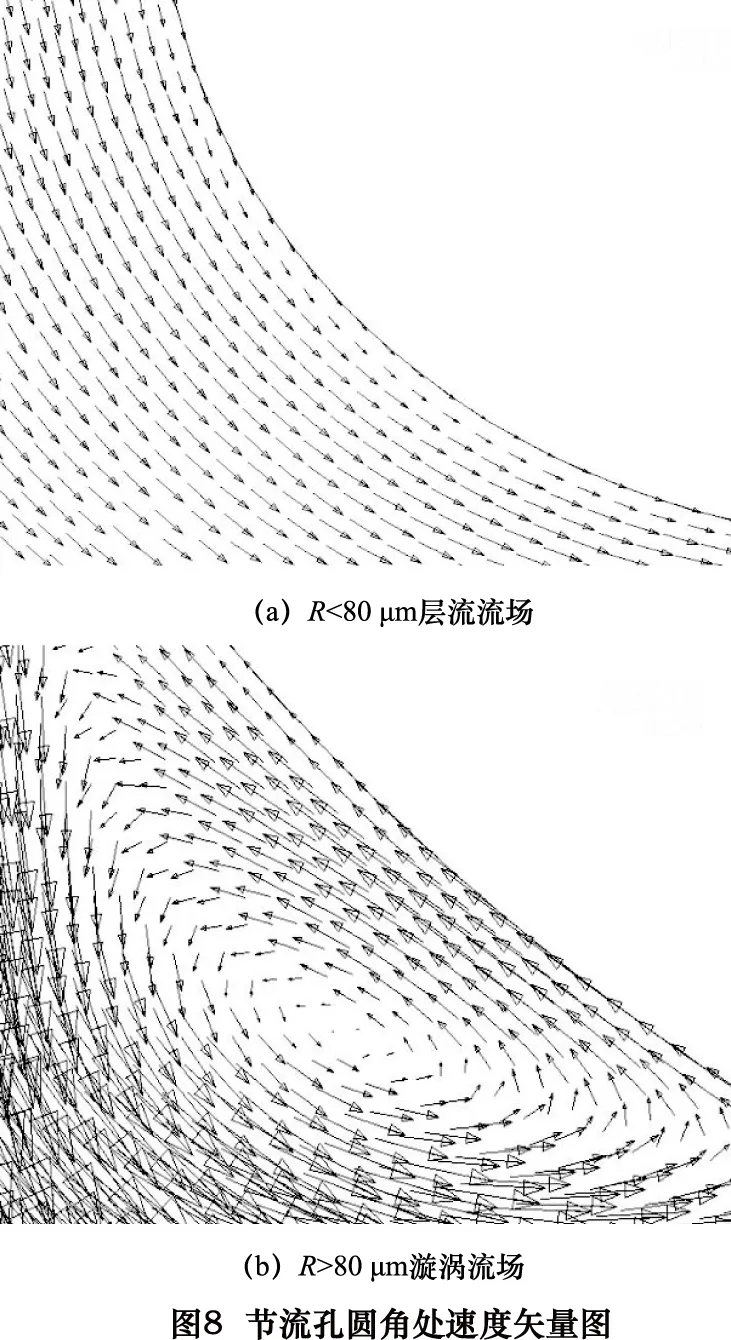
图7显示了不同圆角半径对应的流场最高流速。由图可知，节流孔出口倒圆角，能有效降低流场中最高流速，在一定范围内，圆角半径越大，最高流速越低；随着圆角半径的增大，最高流速的减小趋势放缓，当R>80 μm时，最高流速几乎不再降低，这是由于，如果圆角半径过大，因惯性作用，从节流孔流出的气体将产生分离趋势，不再紧贴圆角壁面运动，过大的出口圆角其导流作用不再突出；同时，由于气流有脱离壁面流动的趋势，在圆角近壁面处的空气流速很低甚至形成滞留，当圆角半径过大(R>80 μm)时，在壁面处还会产生漩涡，其速度矢量如图8所示。根据文献[7],气旋会引起轴承振动，严重影响其稳定性，降低轴承的使用性能。

3　结语

本文利用ANSYS Workbench软件的FLUENT流体分析模块，计算得到小孔气体静压轴承气膜间隙内的压力与速度分布，通过分析节流孔出口圆角对轴承性能的影响，得出如下结论：

(1)节流孔出口采用圆角连接，能减缓出口附近压力陡降，匀化气膜面压力分布，且圆角半径越大，效果越明显。

(2)节流孔出口圆角连接，承载力随圆角半径增大而增大，且增加速率递减，当圆角半径达到一定值，继续增大半径，承载力几乎不再增长。

(3)节流孔出口圆角连接，能有效降低流场中最高流速，在一定范围内，圆角半径越大，最高流速越低；当圆角半径超过一定阈值，节流孔出口处会出现气旋，破坏轴承稳定性。

[1]刘暾, 刘育华, 陈世杰. 静压气体润滑[M]. 哈尔滨:哈尔滨工业大学出版社, 1980．

[2]陈雪梅, 黎文兰. 气体轴承技术及其应用[J]. 润滑与密封, 2000(4): 61-63．

[3]靳兆文. 气体润滑技术及其研究进展[J]. 新技术新产品, 2007(3): 57-59．

[4]邹麒, 肖曙红, 吴利杰. 微小孔阵列式空气静压止推轴承性能研究[J]. 轴承, 2015(2): 48-52．

[5]梁瑞峰, 呼晓青, 刘波，等.表面节流空气静压润滑轴承性能研究[J]. 西安工业学院学报, 2004, 24(1): 1-4．

[6]Chen Xuedong, He Xueming. The effect of the recess shape on performance analysis of the gas lubricated bearing in optical lithography[J]. Tribol.Int. , 2006, 39(11): 1336-1341．

[7]李运堂, 蔺应晓, 朱红霞,等. 基于大涡模拟静压气体推力轴承微幅自激振动特性分析[J]. 机械工程学报, 2013, 49(13): 56-62．

[8]Aoyama T, Kakinuma Y, Kobayashi Y. Numerical and experimental analysis for the small vibration of aerostatic guideways[J]. CIRP Ann. Manuf.Technol, 2006, 55(1): 419-422．

[9]龙威, 李军, 包钢. FLUENT 软件在空气轴承研究领域的应用[J]. 机床与液压, 2006(6): 151-153．

[10]陈改革, 杨涛, 陈立, 等. 静压空气平面轴承特性与节流器间距关系的仿真研究[J]. 西南科技大学学报, 2010, 25(4): 62-67．

[11]吴定柱. 气体静压止推轴承静态性能的数值仿真与实验研究[J]. 密封与润滑, 2010(3): 53-56．

(编辑谭弘颖)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

The effect of rounding orifice restrictor on performance of aerostatic thrust bearings

LI Xiang①，WANG Jie①，YANG Hong②，CUI Hailong②，FANG Hui①

(①School of Manufacture Science and Engineering，Sichuan University，Chengdu 610065,CHN;②Institute of Mechanical Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621900,CHN)

Aerostatic thrust bearing with orifice restrictor was studied, the pressure and velocity distribution of gas film was obtained. This paper presented the performance of aerostatic bearing when the radius of orifice outlet vary. Simulation results showed that, when the gas film thickness kept the same, the load capacity increased and the maximum velocity decreased with the radius of orifice outlet increasing; vortex appeared in the flow field while the radius over limit value, which would reduce the stability of aerostatic bearing.

aerostatic bearing; orifice restrictor; gas film; load capacity; vortex

TH133.35

A

10.19287/j.cnki.1005-2402.2016.06.010

李祥，男，1991年生,硕士研究生，研究方向为超精密加工装备中的静压支承技术。

2015-12-28)

160626

* 国家自然科学基金(51175356) ; 中国工程物理研究院重大科技专项资助(9120602)