汽车排气系统悬挂点位置的优化改进

黄泽好　郑风云　姜广志　袁光亮

重庆理工大学，重庆，400054



汽车排气系统悬挂点位置的优化改进

黄泽好郑风云姜广志袁光亮

重庆理工大学，重庆，400054

为了探究排气系统更优的挂钩位置，对简化模型进行数值分析及理论研究。首先，对挂钩位置的确定进行理论分析并以某乘用车排气系统为研究对象建立有限元模型；其次，分别用平均驱动自由度方法和改进方法确定挂钩位置；最后，将两种方法确定的挂钩位置分别进行动力响应分析并得出结论。改进方法的计算及建模过程耗时更少，工作效率更高；同时，确定的挂钩位置更准确，使得挂钩的力响应更小，传递到车身的振动和结构噪声更不明显。

排气系统；挂钩位置；力响应；结构噪声

0　引言

排气系统作为汽车的重要组成部分，其空间布置及结构决定了振动特性的复杂情况。由发动机传递到排气系统的振动主要通过挂钩传到车身，排气系统悬挂点位置的选择直接影响振动的传递程度，从而影响汽车的乘坐舒适性。因此，排气系统挂钩的潜在位置一直以来都是国内外学者的重要研究对象，本文对传统方法进行了分析与改进[1]。

悬挂点的位置选择主要考虑以下几个方面因素：首先，是否满足空间设计要求；其次，是否满足结构强度要求；最后，是否处于振动过程中的节点位置。针对排气系统悬挂点的选择，当前工程中主要采用平均驱动自由度位移法初步确定挂钩位置[2]。刘名等[3]对排气系统进行了动力学分析，得到排气系统的固有频率并找到振型节点，根据振型节点优化排气系统吊挂位置，有效地减小了排气系统通过吊挂传递到车身底板的力。雷刚等[4]对排气系统自由模态进行了分析，得到系统的固有频率，然后根据平均自由度位移法优化排气系统的挂钩位置，使系统固有频率避开了发动机激励频率。Pang等[5]为排气系统进行前期分析及设计提供了明确的指导方向。然而，在以上研究的过程中并未把整个系统的节点作为输入，而是在系统上选择部分节点，这样分析得到的结果具有不完整性，无法得到挂钩的最佳位置，因为排气系统本身是连续的系统，如果间断地选点可能导致所选两个点之间会有峰值或谷值，获得的挂钩潜在选择点处于峰值和谷值的中间位置，不是最佳位置。笔者在做排气系统悬挂点专题研究时，把整个系统节点做平均驱动自由度位移分析，得到平均驱动自由度位移(average driving degrees of freedom displacement,ADDOFD)的三维云图形式，并用动力响应分析检验优化方法与传统方法的差别，发现三维云图更直观、更准确、更具工程价值，同时，工作效率更高。

1　理论分析

由多自由度系统模态分析理论，对于单点激励，输出点l和输入点p之间的频率响应函数为

(1)

式中，φlr为第l个测点的第r阶模态振型系数；Mr为模态质量；ωr为第r阶模态频率；ξr为第r阶模态阻尼比。

如果激励力的频率为ωr，则近似有

(2)

对线性系统来说，系统的位移响应幅值和频率函数的幅值成正比，则有

(3)

进一步假设振型以质量归一化，各阶模态阻尼近似相等，则有

(4)

在非固有频率下，φlr、φpr相差很大，然而就一般振动而言，都是在固有频率下进行研究。这样，激励和响应相差量接近于零[6](在忽略阻尼的情况下相差量为零)，所以，为了预测某个自由度在一般激励情况下位移响应的相对大小，可定义第j个自由度的ADDOFD值为

(5)

一个节点有6个自由度，然而每个自由度必对应一个节点，这里第j个自由度的平均驱动自由度位移相当于某个节点在该自由度下对应的振动位移。节点的ADDOFD值越小，说明一般激励对该点引发共振的可能性越小。在排气系统悬挂点位置设计中，根据这一理论，一般在空间布置允许的情况下优先选择较小的那些节点位置[7]。

2　模型的建立

汽车排气系统一般分为三部分：热端总成、波纹管、冷端总成。热端一侧连接发动机，另一侧连接波纹管。冷端和热端就通过波纹管连接，作为弹性元件，通过调整其刚度可以改变整个排气系统的振动情况。排气系统冷端通过橡胶吊耳与汽车底盘连接。发动机的有限元模型可以相应简化，但必须通过实验获得发动机质量、质心、转动惯量及悬置点的位置和刚度[8]。吊钩通过橡胶吊耳与底盘连接，橡胶吊耳刚度通过实验获得。同样，波纹管刚度也通过实验获得。使用Hypermesh建立的某排气系统具体有限元模型如图1所示。发动机参数由主机厂提供，见表1。

出于吊耳结构和材料的原因，很难准确地通过实验测得其6个方向的刚度，工程实际中主要考虑到挂钩垂向受力、系统强度及系统一阶横向

图1　排气系统有限元模型

质心坐标(mm)(-210,30,229)I32(kg·m2)0.49质量(kg)186.2I33(kg·m2)12.82I11(kg·m2)6.32Kx(N/mm)180I21(kg·m2)1.08Ky(N/mm)61I22(kg·m2)15.41Kz(N/mm)206I31(kg·m2)3.46

和一阶垂向模态，都是主方向起主导作用。所以一般情况下通过实验获得主方向刚度，而另外几个方向只能根据经验值来建立有限元模型。吊耳主方向刚度测试实验在振动实验台上进行，如图2所示，图中测试的是三孔吊耳，位于后消后挂钩处，因为消声器质量较大，考虑到整个系统的平衡及吊耳的疲劳寿命，则该吊耳的刚度一般比两孔吊耳的刚度大。由于实际情况中橡胶吊耳的压缩主要是起到限位作用，故本文考虑用拉伸实验来测试吊耳刚度。

图2　振动实验台测吊耳静刚度

实验结果如图3所示，吊耳在实验台上受到持续拉伸作用，在拉伸位移为0到0.9 mm时吊耳力与位移关系为非线性，0.9 mm到8 mm为线性均匀变化，在8 mm之后为不规则的振荡变化。所以，吊耳的静刚度取0.9 mm到8 mm这段力与位移关系来计算，得到吊耳的主方向的静刚度为17.6 N/mm。其余吊耳的刚度采取相同的实验方式获得。同样，波纹管也使用实验的方式测得的径向刚度和弯曲刚度分别为8.3 N/mm、3.0 N/mm，得到各个吊耳刚度和波纹管刚度之后采用BUSH单元模拟[9]。

图3　吊耳静刚度测试实验结果

3　有限元分析

3.1平均驱动自由度传统方法确定挂钩位置

沿排气系统轴向从波纹管到尾管将挂钩潜在位置依次布点并编号，这个过程非常费时间，而且所选的点的数量有限，一般情况选择50个点左右[10]。因为发动机怠速转速为800 r/min,最高转速为6000 r/min，所以计算20～200 Hz的所有自由模态，并将振型中这些位置的位移值输出，根据式(5)用MATLAB编写后处理程序提取主方向的振型位移值并将其计权累加，得出ADDOFD曲线与挂钩对应布置位置，如图4所示。

图4　ADDOFD曲线

由图4可知，并不是所有的挂钩位置都选在图中模态位移谷值点，这是因为必须考虑空间位置要求和挂钩受力分布要求。但是，图4中某一段的模态位移谷值点也不一定是实际系统中模态位移最小的点，因为图4中所取点是不连续的，是整个系统的很小一部分具有一定代表性的点。例如，15点与16点之间还有很多点，模态位移谷值点很有可能出现在15、16点之间，也就是说在15、16点之间还有一个比16点更低的点，而且在这两点之间也满足空间及受力要求，那么16点所布的挂钩就不是最理想的位置。笔者在做挂钩位置布置专题研究时，为了提高工作效率并改善其最优效果， 对ADDOFD法进行改进来研究挂钩位置，使用改进方法既省时又更准确。

3.2改进方法确定挂钩位置

改进方法和传统方法一样需要计算20～200 Hz内的自由模态，不同的是改进方法不需要对模型进行单独选点及编号，而是直接将整个模型输入到程序中，节省了大量的时间，减小了工作量。通过模态分析得到排气系统所有节点的振型位移，由于排气系统相对于车架总是在竖直方向振动较为激励，其他自由度方向振动较小，所以将竖直方向的振型位移作为研究对象，根据式(5)用MATLAB编写后处理程序，将其计权累加得到整个系统在该方向的模态位移云图(图5)。

图5　ADDOFD云图

根据图5，挂钩最合适位置非常清楚，在同时考虑空间位置及受力强度的情况下可以非常快速地确定挂钩位置。图5中明显看出1号、5号挂钩处在模态振型位移较大的位置，说明是考虑到受力强度或者在车架上该挂钩位置附近不宜布置挂钩；2号、4号挂钩处在模态振型位移最小的位置，说明这两个挂钩布置得非常准确；3号挂钩明显不是在最优位置，然而通过实车考察，这个挂钩可以作适当调整。

由图4与图5对比可知，改进方法可以非常直观地看出系统模态位移的大小，而且能够确定最小点位置，从而更加准确地确定挂钩位置。由图5可以看出图4中选择的3号挂钩并不是在模态位移最小处，考虑到空间位置及受力的情况，3号挂钩可以适当向左微调，可能会使传递到车身的振动减少。事实上，用传统方法建立模型比改进方法耗费更多的时间，虽然改进方法在后处理程序编写上比传统方法耗时多，但计算时间更少，比较而言改进方法更省时，这一点的工程价值非常明显。虽然传统方法取足够多的点同样能找到最准确的位置，但是这样会耗费更多的时间。综上所述：改进方法更省时，更准确。

3.3动力响应分析验证两种方法确定的挂钩位置

动力响应分析是分析由挂钩传递到车架上的力，这个力是直接影响汽车舒适性的重要指标，正好作为验证两种状态下传递力大小的有效方法[11]。由于受到空间位置和挂钩受力大小限制，并不是所有挂钩都能处于模态位移最小的位置，所以不能验证所有挂钩，选择3号挂钩作为研究对象。图1是包括动力总成的排气系统的动力响应分析模型。

该排气系统与横置四缸发动机匹配，发动机怠速转速为800 r/min，汽车在正常车速下发动机转速一般不会超过4000 r/min，则发动机的扭矩激励频率在26.67～133.33 Hz之间。参考企业标准，加载频率在20～200 Hz之间的大小为100 N·m的绕曲轴中心线的扭矩，在完全约束情况下进行动力响应分析，得到两种状态下3号挂钩约束反力-频率曲线，如图6所示。

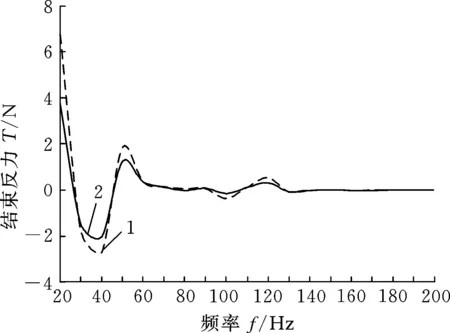
图6　3号挂钩动力响应对比曲线

图6中，曲线1是原状态，曲线2是根据图5在曲线1的基础上把3号挂钩向颜色浅的地方移动45 mm后的状态。从两条曲线明显看出，排气系统在20 Hz、37 Hz、52 Hz频率附近出现较大的传递力，而曲线2从挂钩传递到车身的力比曲线1更小，特别是在20～140 Hz的中低频段，而且20 Hz处出现最大减小约3 N的力，这相对挂钩响应力要求不超过10 N的标准已经有很大程度的改善了。汽车使用过程中，发动机转速范围较多时间在800～4000 r/min之间，激励频率恰好在20～140 Hz之间，如果不尽量通过改变挂钩位置来减小传递到车身的力，很可能在车内会感受到来自排气系统的振动和挂钩传递过来的结构噪声。综上所述，用云图显示的方法确定挂钩位置比传统方法的准确性更高。

4　结论

(1)传统平均驱动自由度法确定挂钩位置较为粗糙，位置确定不够精细，确定的位置不一定是最优位置。

(2)从两种方法确定的位置计算得到的3号挂钩响应力曲线可以看出，改进方法确定的挂钩位置挂钩响应力在低频区域更小，传递到车身的振动和结构噪声更不明显。

(3)改进方法是三维云图形式，挂钩位置根据云图情况来确定，不需要和曲线对比，使得工作效率提高，同时更加直观明了，更具工程价值。

[1]庞剑，谌刚.汽车噪声与振动:理论与应用[M].北京：北京理工大学出版社,2006.

[2]张修路, 姚国凤, 韩春杨, 等.汽车排气系统的悬挂点对减振效果的仿真分析[J].系统仿真学报,2014,26(4): 796-801.

Zhang Xiulu,Yao Guofeng,Han Chunyang,et al.Car Exhaust System of Hanger Point Simulation Analysis of the Vibration Reduction Effect[J].Journal of System Simulation,2014,26(4):796-801.

[3]刘名,翁建生.排气系统振动分析和悬挂点位置优化[J]. 噪声与振动控制,2010,30(5):95-97.

Liu Ming, Weng Jiansheng. Exhaust System Vibration Analysis and the Hanger Point Position Optimization [J].Journal of Noise and Vibration Control,2010, 30(5):95-97.

[4]雷刚,胡鹏,刘圣坤.汽车排气系统模态分析及挂钩位置优化[J].内燃机工程,2014,35(2):102-106.

Lei Gang,Hu Peng,Liu Shengkun.Automotive Exhaust System Modal Analysis and Hanger Position Optimization[J].Journal of Internal Combustion Engine Engineering, 2014, 35(2):102-106.

[5]Pang J,Kurrle P,Qatu M,et al.Attribute Analysis and Criteria for Automotive Exhaust Systems[J].SAE Technical Paper, 2003-01-0221.

[6]Iyer G, Mohan S, Rao N, et al.Evaluation of Dynamic Characteristics of an Automotive Exhaust System Using Operational Modal Analysis (OMA) and Experimental Modal Analysis (EMA)[J].SAE Technical Paper, 2013-01-2903.

[7]刘志恩,田静,颜伏伍,等.汽车排气系统悬挂点布置研究[J].武汉理工大学学报(信息与管理工程版),2010,32(6): 950-953.

Liu Zhien, Tian Jing, Yan Fuwu, et al. Automotive Exhaust System Hanger Point Arrangement Study[J].Journal of Wuhan University of Science and Technology(Information and Management Engineering)2010,32(6):950-953.

[8]Pang J, Qatu M.Exhaust System Robustness Analysis due to Flex Decoupler Stiffness Variation[J].SAE Technical Paper, 2003-01-1649.

[9]黄泽好,郑风云,姜广志,等.基于波纹管简化模型的排气系统模态分析[J].工程设计学报,2015，22(1):54-57.

Huang Zehao,Zheng Fengyun,Jiang Guangzhi,et al. Simplified Model Based on the Corrugated Pipe of Exhaust System Modal Analysis[J].Journal of Engineering Design,2015，22(1):54-57.

[10]Lee C M,Park S T,Kim S H.Development of a Simple Numerical Method of the Exhaust System to Find Optimized Design Values[J].SAE Technical Paper, 1999-01-1666.

[11]Goktan A G, Yetkin A.A Mathematical Model for Exhaust System Vibrations Caused by Road Surface Inputs[J].SAE Technical Paper, 2001-01-1006.

(编辑陈勇)

Hanger Point Location Optimization to Improve Automobile Exhaust System

Huang ZehaoZheng FengyunJiang GuangzhiYuan Guangliang

Chongqing University of Technology, Chongqing,400054

In order to get a better location for the hanger of a exhaust system, this paper was focused on numerical analysis and theoretical research on the simplified model. Firstly, the hanger position was analyzed theoretically and a finite element model was established based on a passenger car. Secondly, the hanger position was determined with the methods of average driver DOF and improved method. Finally, the conclusion was obtained through force response of the two methods’results. It takes less time to calculate and establish a model with improved method, which is proved to be more efficient. Moreover, the location determined by improved method is more accurate, which has a less force response, less shock and less structural noise.

exhaust system,；hanger position；force response；structural noise

2015-10-10

2013年重庆高校创新团队建设计划资助项目(KJTD201319)

TH122；U463.1DOI：10.3969/j.issn.1004-132X.2016.15.021

黄泽好，男，1966年生。重庆理工大学车辆工程学院教授。主要研究方向为车辆系统动力学、车辆动噪声的分析和控制。发表论文30余篇。获省部级科技进步一等奖1项、二等奖2项、三等奖5项。郑风云，男，1989年生。重庆理工大学车辆工程学院硕士研究生。姜广志，男，1990年生。重庆理工大学车辆工程学院硕士研究生。袁光亮，男，1990年生。重庆理工大学车辆工程学院硕士研究生。