亚波长二维光栅结构零级透射场的计算方法
马 平,黄训铭,邓 浩,石安华,黄 洁
(1.中国空气动力研究与发展中心超高速所,四川 绵阳 621000; 2.电子科技大学 物理电子学院,成都 610054)
亚波长二维光栅结构零级透射场的计算方法
马平1,黄训铭1,邓浩2,石安华1,黄洁1
(1.中国空气动力研究与发展中心超高速所,四川 绵阳621000; 2.电子科技大学 物理电子学院,成都610054)
基于散射度量术中测量掩膜版时对零级透射率波谱的计算需求,将需要阶梯近似分层的复杂二维光栅统一模型化为多层二维光栅,建立了多层二维光栅零级透射场计算方法;将Moharam传输矩阵法的部分解法推广到一般复杂二维光栅结构,实现对多层或者非垂直侧壁结构透射场的逐层迭代计算;对一种亚波长二维金属光栅阵列结构进行了宽谱光源入射下的透射特性仿真计算;结果表明:结合二维光栅模拟的收敛性改进算法,建立的计算方法能实现对复杂二维光栅透射率波谱的求解。
衍射;光栅;严格耦合波分析;传输矩阵法;散射度量术
本文引用格式:马平,黄训铭,邓浩,等.亚波长二维光栅结构零级透射场的计算方法[J].兵器装备工程学报,2016(8):155-159.
光栅零级衍射场的模拟计算对分析与设计光栅、光子晶体等周期结构具有重要意义[1-3]。此外,它在微电子半导体集成电路结构的分析/测试技术中也有着广泛的应用[4]。其中,光栅透射场的计算是散射度量术中测量掩膜版等透明材料的一个重要环节[5]。传统的光栅零级衍射场计算方法主要采用标量衍射模型。随着半导体技术节点的不断更新以及半导体工艺的持续发展,以亚波长尺寸3D结构为代表的复杂二维光栅结构大量出现,矢量衍射模型逐渐成为主流。其中,严格耦合波分析(RCWA)是目前应用最广泛的高效、稳定的方法[6]。它对于垂直侧壁周期结构的衍射模拟具有极高效率,对于复杂非垂直侧壁结构则需通过沿光栅侧壁方向阶梯近似分层计算[7-8]。对于亚波长光栅,只存在零级衍射传播波,其余级次均为不携带能量的倏逝波[9]。零级透射场的计算分析对于确定亚波长光栅的透射特性至关重要。目前,针对复杂二维光栅结构零级透射场模拟的研究较少。根据文献[9]的观点,传输矩阵法相对于传统S-矩阵法更直接高效。Moharam只给出了一维情况下的反射率计算方法,对于透射率以及更复杂的二维情况并没有具体说明。本文在Moharam的部分解法的基础上,将需要阶梯近似分层的复杂二维光栅统一模型化为多层二维光栅,最终通过逐层迭代计算宽谱光源入射情况下二维问题的零级透射场。
1 理论模型
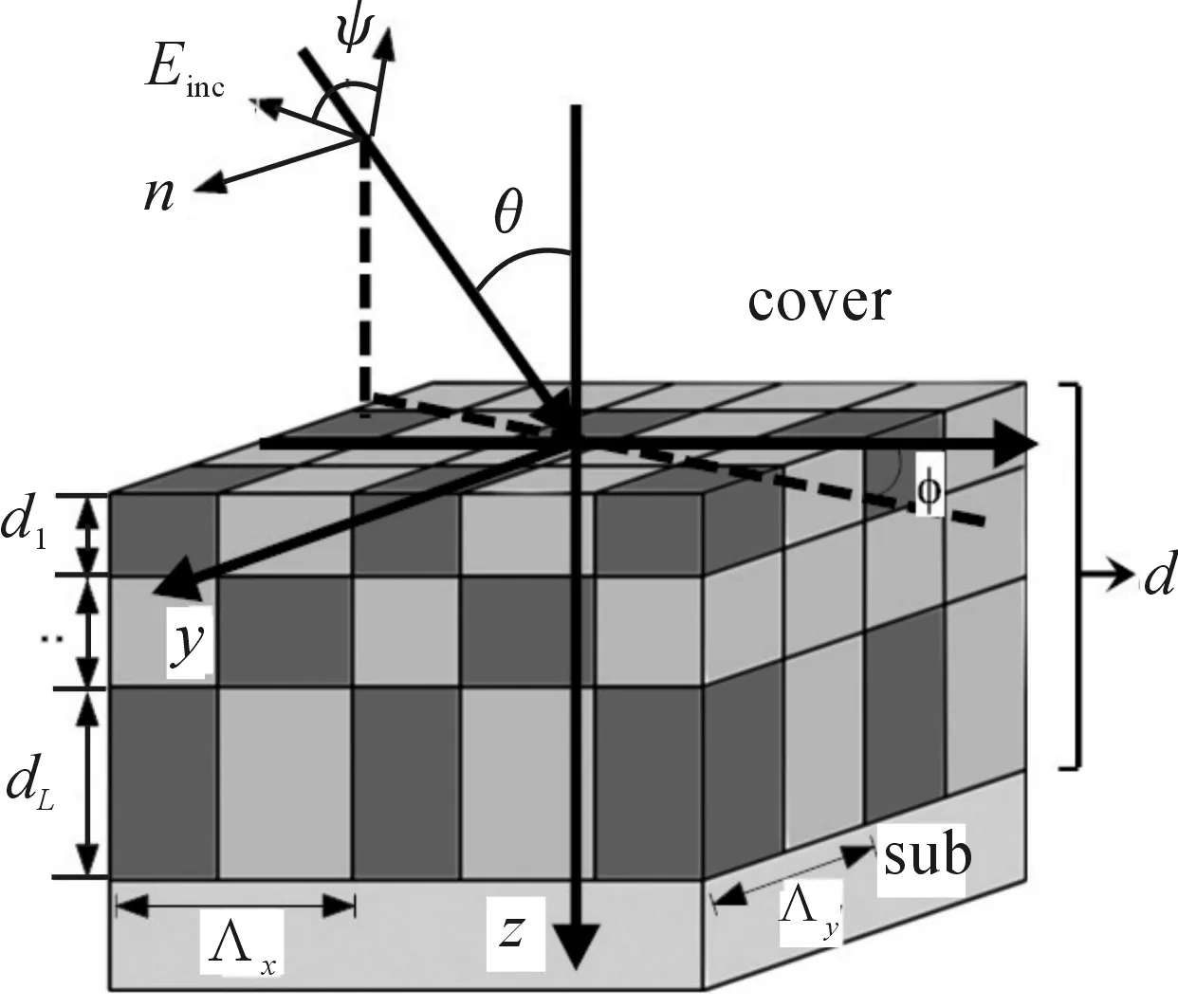
图1 亚波长复杂二维光栅的多层模型
对此二维问题,其入射电场定义:
(1)
其中,
(2)
在光栅区域,光的传播将受到二维光栅在两个方向上的周期性变化的调制,最终通过弗洛奎特条件反映到电磁波在各个问题区域的平面波谐波展开形式上。因此,光栅区域(各阶梯近似层内)的归一化电磁场可以表示为如下的谐波形式:
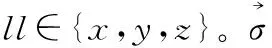
(5)
式(5)中:Kx=2π/Λx,Ky=2π/Λy,Λx,Λy为x,y方向周期。
待定的Sll,m,n(z)与Ull,m,n(z)可以通过求解光栅区域各层的特征值问题给出其谐波展开形式。该二维光栅的特征值问题则通过如下微分方程表述:
(6)
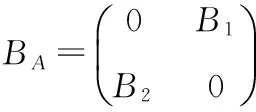
各层内,微分方程(6)的通解表示为如下谐波展开形式:
(7)
(8)
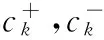
(9)
对于任意复杂二维光栅透射问题,均可通过对复杂光栅结构实现阶梯近似后将各层的通解式(7)、式(8)代入层间电磁场的切向连续边界条件,并结合覆盖层与衬底层的电磁场谐波展开式,计算其各阶透射衍射效率。其中,覆盖层与衬底层的电场谐波展开式表示为:
(10)
(11)

(12)
通过求解各阶梯近似层内的特征值问题,并自覆盖层到衬底层逐层的结合各层间边界条件方程,最终计算任意介质复杂二维光栅的透射率。
2 多层二维光栅零级透射场算法
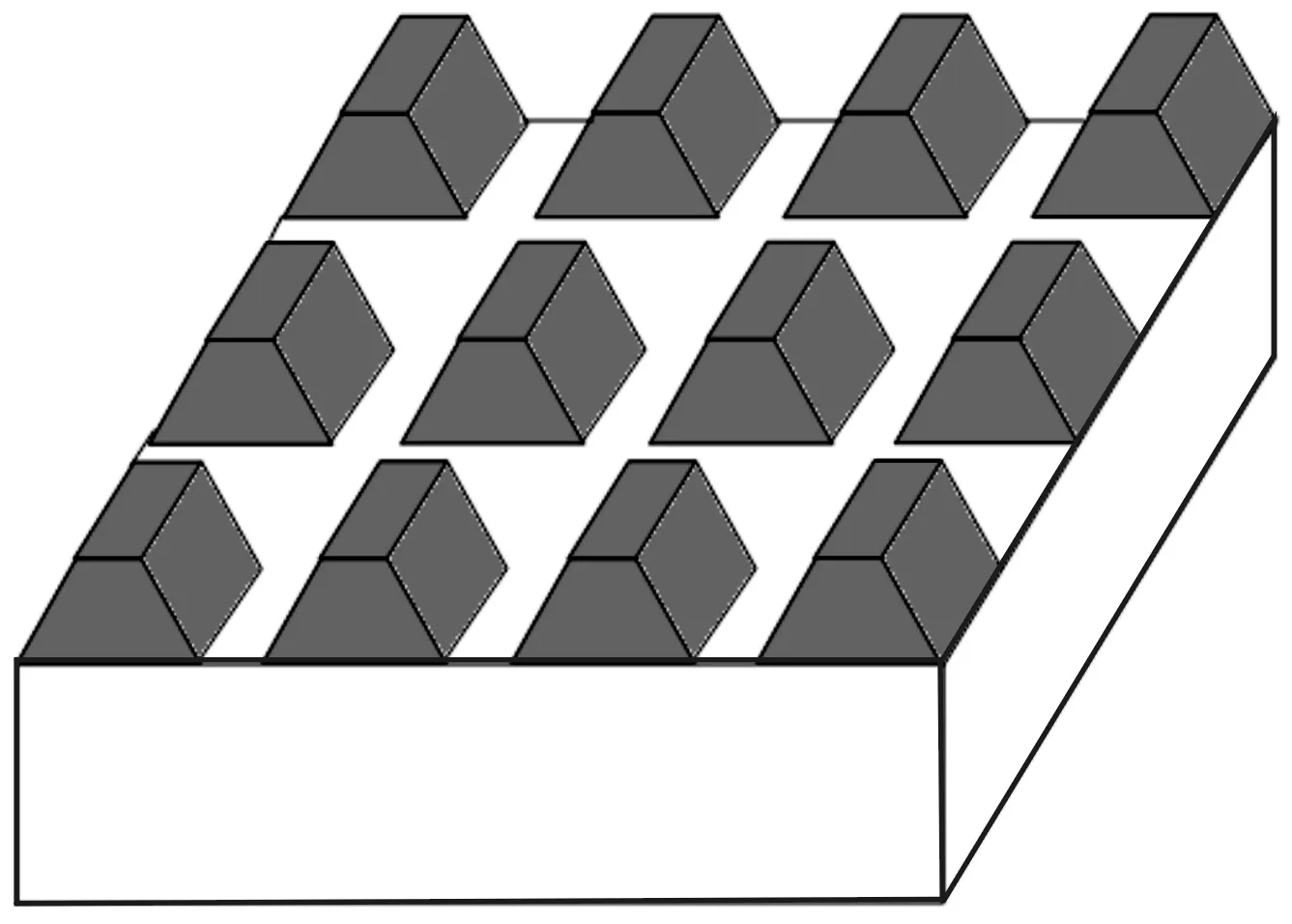
根据上节所述多层二维光栅模型,令各层的特征问题相关矩阵为Wl,Vl(其中,0 首先,在边界z=0处,通过匹配各层间的切向电场与切向磁场,边界条件方程可以写为 (16) (17) (18) 然后,式(18)进一步改写为 (19) 其中, 令f1=W1(X1a1+I),g1=V1(I-X1a1),那么 (20) 其次,在第1层与第2层边界处,边界条件方程可以写为 (21) 由此得到: (22) (23) 类似的,可以继续给出f2,g2和B2。 (24) (25) (26) 在最后一层(l=L)与衬底边界处,边界条件方程可以写为: (27) (28) 对于零级透射率而言,Tx,00,Ty,00由式(28)得到,Tz,00则可以通过下式计算: (29) 二维光栅的零级透射率T00为Tx,00、Ty,00、Tz,00平方和的方根。需要注意的是由于衬底介质的存在,实际的透射率是在衬底层之外检测到,因此最终计算结果需要考虑衬底层与空气边界对T00的多重反射效应。此外,由于二维光栅结构往往还会带来严重的收敛性问题,实际应用过程中通过采用一些收敛性改进方案,比如Lalanne的经验法[11]与Schuster的垂直矢量法[12]等,提高其计算收敛速度。 图2为参考自文献[13]中实现高透射调制的一种二维亚波长金属阵列结构,其x与y方向周期为120 nm。该结构为非垂直侧壁,其x方向上底矩形长为90 nm(占空比为0.75),下底矩形长为108 nm(占空比fx=0.9);其y方向上下底矩形宽为66 nm(占空比fy=0.55),衬底为SiO2,金属材料为Al,光栅厚度为140 nm。实际半导体集成电路分析/测试工程中通常采用宽谱光源入射,因此对于波长为190~1 100 nm垂直入射的TE偏振平面波(由于坐标系的区别,对应文献13中的TM偏振),采用色散折射率数据计算。本文采用Lalanne的经验法提高其收敛速度,其阶梯近似数选择为5层,最大谐波阶次M、N均选择为10,其零级透射率波谱计算结果如图3所示。从图3可以看出,该亚波长金属阵列结构的光栅TE波具有较高透射特性,其透射光的零级衍射率大于60%;随着入射光波长的增加,光栅衍射效率增加。因此,本文建立的多层二维光栅零级透射场计算方法能够有效地计算分析二维光栅的零级透射场,为分析复杂二维光栅的透射特性提供了一种新方法。 图2 非垂直侧壁金属阵列光栅 图3金属阵列光栅零级透射率波谱计算结果 本文给出了复杂二维光栅零级透射率的逐层迭代计算方法,该方法适用于任意二维光栅结构。对于复杂的亚波长多层结构或者非垂直侧壁的周期结构均可以实现数值稳定的迭代计算。由于二维结构往往需要考虑傅里叶级数展开过程所带来的收敛问题[14],实际的严格耦合波应用中通常还需采用适当的收敛性改进方法,以提高收敛效果。本文所述方法为Moharam传输矩阵法的部分解法在二维透射计算问题的拓展,能有效计算各种复杂二维结构的零级透射率波谱,并应用于微电子半导体集成电路结构的分析与测试应用之中。 [1]赵华君.亚波长介质偏振分束光栅的衍射特性[J].强激光与粒子束,2008,20(10):1629-1632. [2]周云,申溯,叶燕,等.带有高折射率介质层的金属光栅偏振器特性的研究[J].光学学报,2010,30(4):1158-1161. [3]童凯,曾文智,谷朝聪,等.覆层介质对光子晶体生物传感器灵敏度的影响[J].中国激光,2013,40(2):02140021-02140026. [4]CHALYKH R,PUNDALEVA I,KIM S,et al.Simulation of critical dimension and profile metrology based on scatterometry method[C]//Proc.SPIE 6349,2006,63491K1-63491K9. [5]PERLICH J,KAMM F M,RAU J,et al.Characterization of extreme ultraviolet masks by extreme ultraviolet scatterometry[J].J Vac Sci Technol B,2004,22(6):3059-3062. [6]MOHARAM M G,GAYLORD T K.Rigorous coupled-wave analysis of planar-grating diffraction[J].J Opt Soc Am,1981,71(7):811-818. [7]MOHARAM M G.POMMET D A,GRANN E B,et al.Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings:enhanced transmittance matrix approach[J]. J Opt Soc Am A,1995,12(5):1077-1086. [8]LI LIFENG.Formulation and comparison of two recursive matrix alogrithms for modeling layered diffraction gratings[J].J Opt Soc Am A,1996,13(5):1024-1035. [9]TAN E L.Note on formulation of the enhanced scattering-(transmittance-) matrix approach[J].J Opt Soc Am A,2002,19(6):1157-1161.[10]DENG H,CHEN S.Efficient implementation of Fourier modal slice absorption method for lamellar crossed gratings[J].Optical Engineering,2013,52(6):0682011- 06820111.[11]LALANNE P.Improved formulation of the couple-wave method for two-dimensional gratings[J].J Opt Soc Am A,1997,14(7):1592-1598. [12]SCHUSTER T,RUOFF J,KERWIEN N,et al.Normal vector method for convergence improvement using the RCWA for crossed gratings[J].J Opt Soc Am A,2007,24(9):2880-2890. [13]陈娟,闫连山,潘炜,等.二维金属矩形光栅的偏振控制及其透射特性[J].光学学报,2011,31(12):12240011-12240015. [14]LI L F.Use of Fourier series in the analysis of discontinuous periodic structures[J].J Opt Soc Am A,1996,13(9):1870-1876. (责任编辑唐定国) Calculation Zero-Order Transmittance for Sub-Wavelength Multilayered Two-Dimensional Gratings MA Ping1, HUANG Xun-ming1,DENG Hao2, SHI An-hua1,HUANG Jie1 (1.Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang 621900, China; 2.School of Physical Electronics, University of Electronic Science and Technology of China, Chengdu 610054, China) Based on the needs for calculation of the zero-order transmittance spectrum in scatterometry, the complex two-dimensional gratings needed to divide into many echelons that are equivalent to multilayer two-dimensional gratings. The computing method of the zero-order transmission field of those was put forward. The partial-solution of the enhanced transmittance matrix approach was generalized to arbitrary two-dimensional gratings. This approach was shown to produce numerically stable iterative-calculation results for multilevel or slanted gratings. A sub-wavelength two-dimensional metallic grating was analyzed. Simulation results show that this approach is efficient for the calculation of transmittance for general two-dimensional gratings with a preferred convergence-improved method. The computing method can be used to solve the transmissivity spectrum of the complex two-dimensional grating. diffraction; grating; rigorous couple wave analysis; enhanced transmittance matrix approach; scatterometry 2016-02-29; 2016-04-18 国家重大基础研究发展计划项目(2014CB340202);国家自然科学基金项目(11272336) 马平(1976—),男,高级工程师,主要从事超高速目标光电特性、再入通讯中断等研究。 10.11809/scbgxb2016.08.035 format:MA Ping, HUANG Xun-ming,DENG Hao, et al.Calculation Zero-Order Transmittance for Sub-Wavelength Multilayered Two-Dimensional Gratings[J].Journal of Ordnance Equipment Engineering,2016(8):155-159. O436 A 2096-2304(2016)08-0155-05 【光学工程与电子技术】
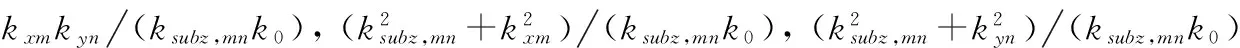
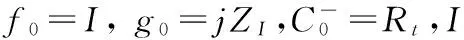
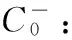



3 数值模拟与分析

4 结论

