基于RBF神经网络的滚仰式导引头控制系统设计

贾晓洪,韩宇萌,王炜强

(中国空空导弹研究院，河南 洛阳　471009)



基于RBF神经网络的滚仰式导引头控制系统设计

贾晓洪,韩宇萌,王炜强

(中国空空导弹研究院，河南 洛阳471009)

为保证滚仰式捷联导引头的稳定控制，提出了一种基于RBF神经网络整定的PID控制策略，用于导引头稳定回路校正环节。根据滚仰式捷联导引头的运动学与动力学关系，结合导引头稳定回路校正环节采用的RBF神经网络PID控制算法，建立了滚仰式捷联导引头稳定与跟踪一体化仿真模型；仿真结果表明：滚仰式捷联导引头稳定回路采用RBF神经网络整定的PID控制器后，其动态性能优于传统PID控制器，建立的仿真模型能够对机动目标实现快速稳定跟踪，在工程应用中可提供有益参考。

滚仰式导引头；稳定平台；伺服控制；RBF神经网络；PID参数整定

本文引用格式：贾晓洪,韩宇萌,王炜强.基于RBF神经网络的滚仰式导引头控制系统设计[J].兵器装备工程学报，2016(8):1-5.

tuning

为适应现代近距格斗空空导弹高机动性及大离轴角发射的要求，导引头伺服稳定平台就要实现大跟踪场、高跟踪角速度[1-2]。滚仰式导引头伺服稳定平台结构具有体积小、跟踪场大、大离轴发射能力，视场可以覆盖整个前半球，做到“看见即发射”，可以大大减少对载机发射占位的要求[3-6]，其结构如图1所示。由于受到弹体姿态变化、外部高速气流冲击、气动力扰动等因素的影响，使得空空导弹的整个弹体处于复杂运动状态[7]，对导引头的稳定控制也产生了严重不良影响，使得常规的PID控制方法难以满足精度要求。

图1　滚仰式捷联导引头结构示意图

神经网络能够逼近任意的非线性映射关系，可以对非线性系统及不确定系统有效控制[8]。神经网络在滚仰式导引头伺服稳定平台控制系统中的应用，可以提高控制系统的智能化水平和适应能力。本文针对常规PID控制方法控制精度要求低的问题，提出了一种基于RBF神经网络整定的PID控制策略，用于滚仰式导引头伺服稳定平台，使伺服稳定平台的控制系统具有更高的跟踪精度和更好的鲁棒性。

1　导引头稳定跟踪原理

图2　滚仰式导引头稳定跟踪原理

1.1运动学关系

滚仰式稳定平台采用滚转+俯仰两轴极坐标结构形式，其外框架为滚转框架，内框架为俯仰框架。通过采用这种结构形式，可以实现大离轴角条件下对目标的探测与跟踪。对滚仰式导引头运动学原理分析可以得到稳定平台的运动耦合传递机理，为滚仰式导引头动力学建模和伺服稳定控制研究提供依据[10]。

(1)

(2)

为了使导引头光轴在惯性空间内的指向保持稳定，令式(2)中ωiy=0，ωiz=0，得到光轴稳定时外框架和内框架的转动指令如下：

(3)

1.2动力学关系

导引头稳定平台框架的结构形式、质量分布等都会对动力学系统的性能产生影响。根据刚体绕定点运动的欧拉动力学方程，内框的动力学方程为：

(4)

(5)

若考虑俯仰内框架的电缆约束力矩、摩擦力矩、质量不平衡力矩等，则又存在如下关系：

(6)

其中，Tiz为内框架俯仰电机的控制力矩；Tumbi为内框架的质量不平衡力矩；Tfi为内框架的摩擦力矩；Tsi为内框架的电缆约束力矩，并且：

(7)

根据式(5)和式(6)，可得内框架的动力学方程：

(8)

按运动学关系将式(8)展开，得内框电机的驱动力矩为

(9)

其中，Tgci为外框对内框的交叉耦合项，Tmci为弹体与内框的交叉耦合项。

导引头滚转外框架除了自身的转动力矩作用外还有内框的反作用力矩，其动力学方程为

(10)

得到外框架动力学模型：

(11)

1.3控制信号指令

采用导引头方位角和高低角εy、εz及平台内外框架角θs和γs解算稳定平台内外框架角误差Δθs、Δγs，形成稳定跟踪指令如下：

(12)

2　基于RBF神经网络的PID控制算法

2.1RBF神经网络

径向基函数(Radial Basis Function,RBF)神经网络结构是一种局部逼近的网络结构，它能以任意精度逼近任意连续函数。RBF神经网络输入到输出的映射是非线性的，隐含层到输出的映射是线性的，这种结构形式在提高学习速度的同时避免了局部极小问题[11-12]。RBF神经网络结构如图3所示。

图3　RBF神经网络结构

设X=[x1，x2，…，xn]T为RBF神经网络的输入向量，H=[h1，h2，…，hj,…，hm]T为其径向基向量，hj为高斯基函数：

(13)

式(3)中Cj为第j个结点的中心矢量：

(14)

设神经网络的基宽向量为B=[b1,b2,…,bm]T，网络的权向量为W=[w1,w2,…,wj,…,wm]T，辨识网络的输出为

ym(k)=w1h1+w2h2+…+wmhm

(15)

辨识器的性能指标函数：

(16)

根据梯度下降法，输出权向量、节点基宽参数及节点中心向量的迭代算法分别如下：

(19)

式(19)中，η为学习速率，α为动量因子。

Jacobian算法为

(20)

2.2RBF神经网络PID整定原理

滚仰式稳定平台伺服控制回路采用增量式PID控制器，基于RBF神经网络PID整定原理如图4所示。

图4　RBF神经网络PID整定原理

PID控制器其控制误差为

error(k)=rin(k)-yout(k)

(21)

控制器的3项输入分别为

(22)

控制器的控制算法为

(23)

神经网络整定指标可由下式计算：

(24)

采用梯度下降法调整kp、ki、kd，调整量如下：

(25)

3　仿真分析

根据滚仰式导引头稳定与跟踪原理，导引头伺服控制回路采用基于RBF神经网络整定的PID控制器，利用Matlab/Simulink建立仿真模型如图5所示，对导引头的稳定与跟踪性能进行验证。

图5　滚仰式导引头仿真模型

为了验证RBF神经网络控制器，取采样时间t=0.001 s,学习速率η=0.25,动量因子α=0.05。导引头稳定平台框架角误差给定1°的阶跃信号时，导引头稳定跟踪系统的阶跃响应曲线如图6所示。与传统PID控制器相比，基于RBF神经网络整定的PID控制器的响应调节时间ts由0.21 s减小到0.14 s，上升时间tr由0.09 s减小到0.06 s，阶跃响应的超调量σ%由19%减小到16%，由此可知导引头控制系统采用基于RBF神经网络整定的PID控制器后，其动态性能比采用常规PID控制器的动态性能优异。内环框架开环幅频特性如图7所示，幅值裕度10.5 dB，幅值交接频率125 rad/s，相位裕度53.3 deg，相位交接频率36.2 rad/s。外环框架开环幅频特性如图8所示，幅值裕度8.75 dB，幅值交接频率128 rad/s，相位裕度55.9 deg，相位交接频率45.6 rad/s。

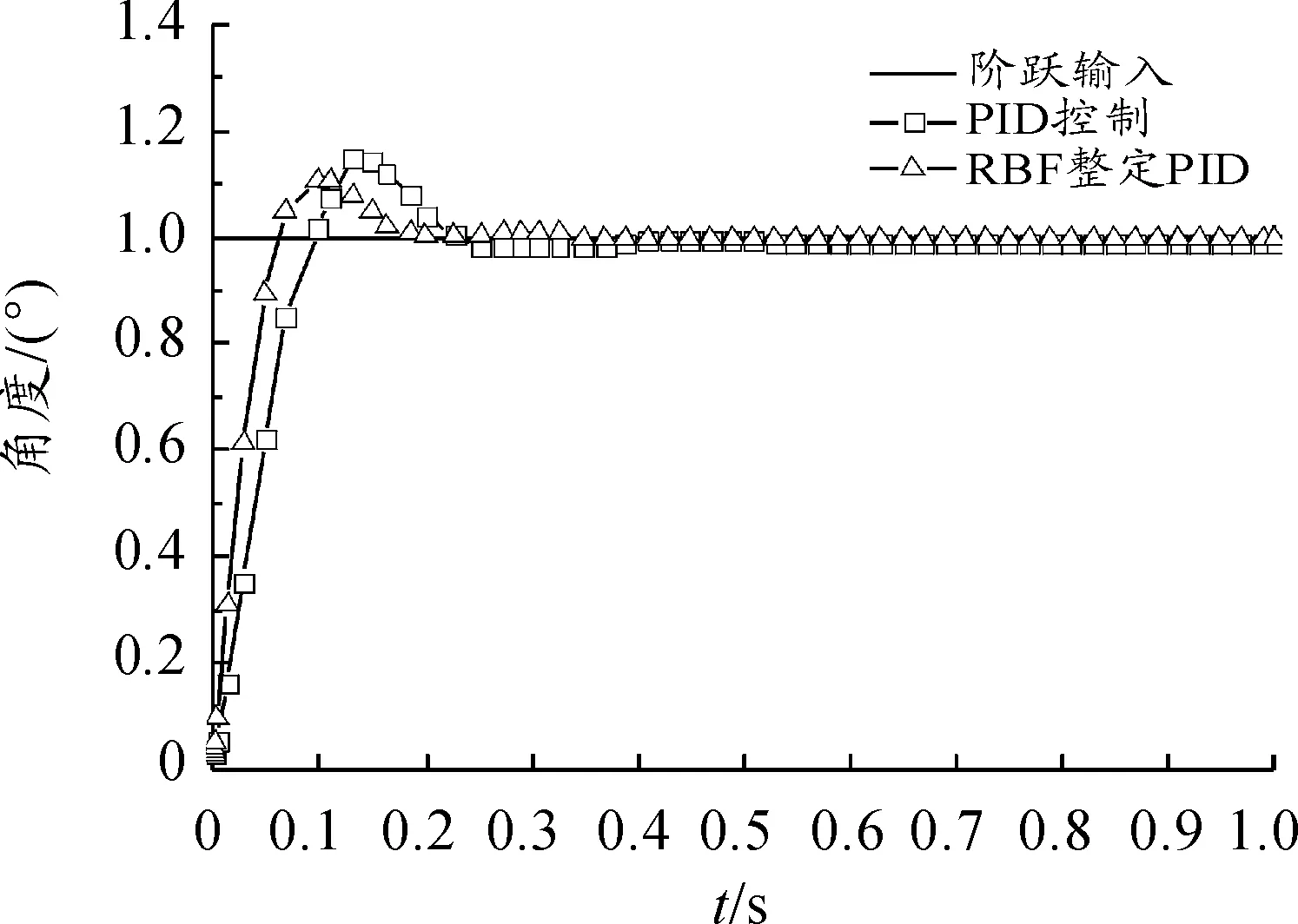
图6　导引头跟踪系统的阶跃响应

图7　内环位置回路开环幅频特性

图8　外环位置回路开环幅频特性

假定目标在惯性空间做圆周运动，根据图5所示的仿真模型验证导引头对运动目标的跟踪性能。由图9、图10可知，在0.15 s内导引头可完成对目标的稳定跟踪，稳定平台内外框架能够根据目标的运动状态持续稳定的对目标跟踪。目标在导引头视场中的运动轨迹如图11所示，可以看出目标始终在导引头视场内，导引头能稳定的跟踪目标。

图9　目标运动情况下光轴误差角εy

图10　外环滚转框架角变化曲线

图11　目标在导引头视场中的运动轨迹

4　结论

针对滚仰式导引头控制回路设计了一种基于RBF神经网络整定的PID控制器，建立了稳定与跟踪的一体化仿真模型。根据导引头框架角误差信号，通过学习在线调整kp、ki、kd3个参数，实现具有最佳组合的PID控制。基于RBF神经网络整定PID控制器可以提高导引头控制系统的响应速度，减小系统的超调量，使导引头控制回路的自适应能力得到提高，能够实现对目标的快速稳定跟踪，使目标持续有效的稳定在视场内，在实际工程应用中能够为导引头的控制提供有益的参考。

[1]崔大朋,苏建平.精确制导武器稳定平台技术[J].四川兵工学报,2015,36(5):35-38.

[2]周卫文,梁晓庚,贾晓洪.平台式导引头跟踪回路对制导系统的影响[J].四川兵工学报,2011,32(5):1-4.

[3]王志伟,祈载康,王江.滚-仰式导引头跟踪原理[J].红外与激光工程,2008,37(2):274-277.

[4]夏晓雷.框架式导引头控制技术[J].四川工兵学报,2011,32(9):43-50.

[5]耿峰,祝小平.精确制导武器红外成像导引头控制系统研究[J].宇航学报,2007,28(3):535-538.

[6]付奎生.两轴捷联稳定跟踪平台关键技术分析[J].电光与控制,2009,16(7):53-55.

[7]ZARCHAN P.Tactical and Strategic Missile Guidance[M].Massachusetts:American Institute of Aeronautics and Astronautics,2012.

[8]刘金琨.智能控制[M].北京:电子工业出版社,2014.

[9]肖仁鑫,张聘义,胡海双,等.滚俯仰式红外导引头稳定平台控制与仿真[J].红外与激光工程,2007,36(增刊):39-42.

[10]陈雨,赵剡,张同贺，等.滚仰式捷联导引头跟踪原理与仿真[J].航空兵器,2010(5):55-58.

[11]强勇,凌有铸,贾冕茜.基于RBF神经网络的永磁同步电机速度控制[J].微电机,2013,46(4):53-56.

[12]乔俊飞,韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报,2010,36(6):865-872.

(责任编辑周江川)

Control System Design Based on RBF Neural Network for Roll-Pitch Seeker

JIA Xiao-hong, HAN Yu-meng, WANG Wei-qiang

(China Airborne Missile Academy, Luoyang 471009, China)

To solve the stability control of roll-pitch strap-down seeker, one kind of PID self-tuning algorithm based on RBF neural network was put forward for the stable loop correction link of the seeker. According to the kinematics and dynamics model of the roll-pitch strap-down seeker, the stability and tracking integrated model was established by using RBF neural network PID controller algorithm. Simulation results show the dynamic performance of PID self-tuning algorithm based on RBF neural network is superior to traditional PID controller for the roll-pitch strap-down seeker. The simulation model of the stability and tracking integrated model not only has stable quickly tracking ability for the maneuvering target, but also can provide a useful reference in the engineering application.

roll-pitch seeker; stabilized platform; servo control; RBF neural network; PID parameter

2016-02-23；

2016-03-20

贾晓洪(1968—)，男，研究员，博士，主要从事飞行器控制、制导与仿真研究。

10.11809/scbgxb2016.08.001

format:JIA Xiao-hong, HAN Yu-meng, WANG Wei-qiang.Control System Design Based on RBF Neural Network for Roll-Pitch Seeker[J].Journal of Ordnance Equipment Engineering,2016(8):1-5.

TJ765.3

A

2096-2304(2016)08-0001-05

【装备理论与装备技术】