从折叠与展开视角看立体几何问题的解答

☉华中师范大学第一附属中学 黄文韬

从折叠与展开视角看立体几何问题的解答

☉华中师范大学第一附属中学 黄文韬

折叠与展开问题是立体几何的两个重要问题，这两种方式的转变正是空间几何与平面几何问题转化的集中体现.处理这类题型的关键是抓住两图的特征关系.平面图形通过折叠变成立体图形；立体图形通过展开变成平面图形.这类问题的解决主要是弄清它们之间的位置关系和度量关系.要善于将立体问题转化为平面问题.

例1 （2016年浙江卷）如图1，在△ABC中，AB=BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是_________.

图1

常规解答：△ABC中，因为AB=BC=2，∠ABC=120°，所以∠BAD=∠BCA=30°.由余弦定理可得AC2=AB2+BC2-2AB·BCcosB=22+22-2×2×2cos120°=12，所以AC=2

在△ABD中，由余弦定理可得BD2=AD2+AB2-2AD· ABcosA=x2+22-2x·2cos30°=x2-2x +4.故BD=

在△PBD中，PD=AD=x，PB=BA=2.

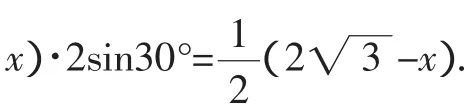
设PO与平面ABC所成角为θ，则点P到平面ABC的距离h=dsinθ.

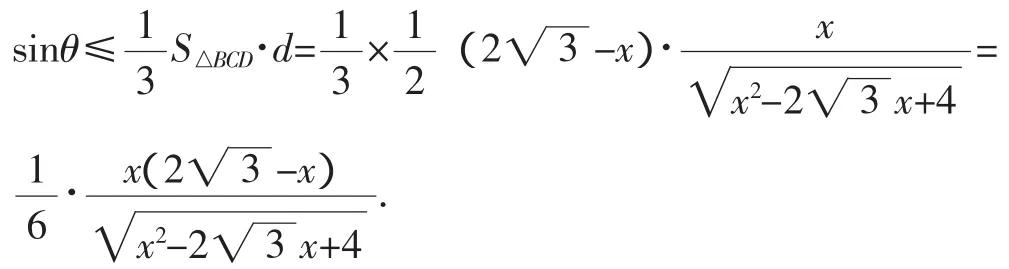
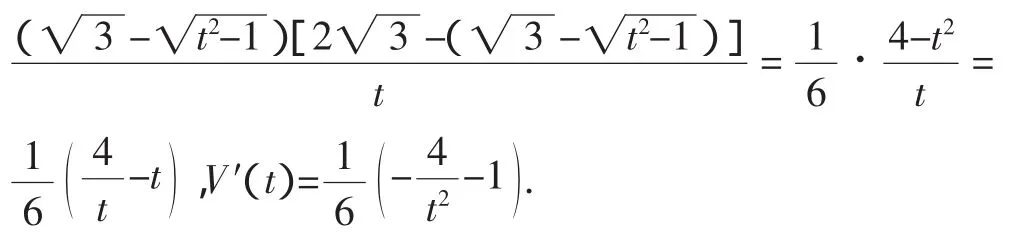
因为1≤t≤2，所以V′（t）＜0，所以函数V（t）在区间［1，2］上单调递减，故V（t）≤V（1）=

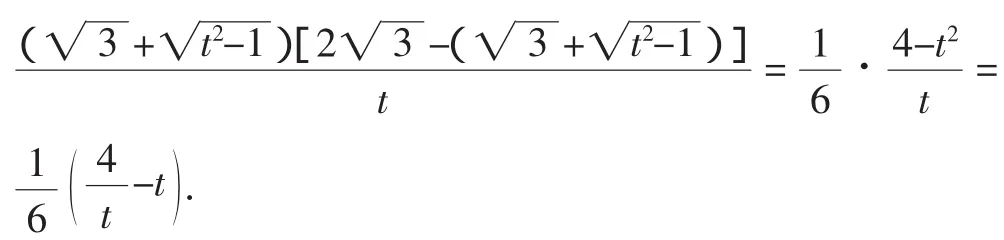
由以上可知，函数V（t）在（1，2］上单调递减，故

空间问题平面化是处理立体几何问题的有效策略，对于某些特殊的几何体可将其视为由平面几何图形通过旋转或翻折得到的，解题中即可利用相应平面几何图形的性质求解，可化繁为简.

优化解答：根据题目特征，本题可以理解为△PBD是由△ABD绕着BD旋转得到的，对于每段固定的AD，底面△BCD的面积为定值，要使体积最大，则△PBD⊥面ABC，此时高最大，体积也最大.具体解析过程如下：

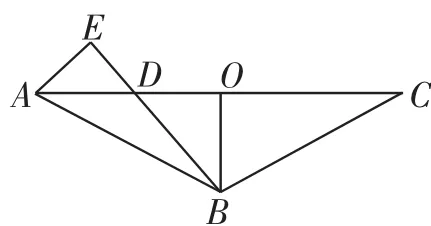
图2

图3

一、借助菱形的翻折变换

例2 如图4，四面体ABCD的一条棱长为x，其余棱长均为1，记四面体ABCD的体积为F（x），则函数F（x）的单调增区间是_________；最大值为__________.

解析：根据四面体的结构特点，四面体ABCD可视为∠CAD=60°的菱形ABCD，沿对角线CD折叠而成.

图4

随着x值的增大，四面体ABCD的体积逐渐增大，并且当面ACD⊥面BCD时，体积达到最大值，此时易求得，故

评注：本题求解中根据题目特征，将已知几何体平面化，再借助平面图形即菱形的翻折变换，得到已知几何体，再根据翻折过程中相关量的变化趋势，实现了对问题的简洁求解.

二、借助正方形翻折变换

解析：根据题目特征，已知四面体相当于将边长为1的正方形ABCD沿着对角线BD折叠而成.如图5所示，则长为a的棱即为AC，而0＜AC＜.故正确选项为A.

图5

评注：本题的求解中将空间问题平面化，寻找特殊的平面几何图形，即正方形，通过正方形的翻折变换，得到满足条件的几何体.再借助正方形相关量的变化范围得到所求几何体相关量的范围.

三、以翻折变换为条件

例4 （2015年陕西卷理）如图6所示，在直角梯形ABCD中，AD∥BC，∠BAD=，AB=BC=1，AD=2，E是AD的中点，O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置，如图7所示.

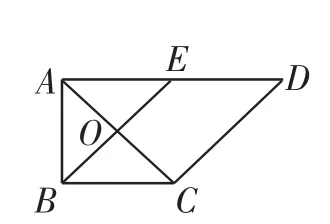
图6

图7

（1）证明：CD⊥平面A1OC；

（2）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD夹角的余弦值.

分析：这是一个将平面图形通过翻折得到空间图形，进而论证空间图形形成过程中的位置关系，计算空间角等问题.我们在解决此题时，一定要抓住图形在翻折过程中，保持不变的关系和不变的量.因为△ABE沿BE折起，这个过程中，不变的是△ABE，四边形BCDE.在图6中，我们易于发现四边形ABCE是正方形，AC⊥BE，在图7中有BE⊥AO，BE⊥CO，可得BE⊥平面A1OC，再由CD∥BE，第（1）问得证，对于第（2）问，我们可能建立直角坐标系，用向量的方法通过代数运算求解.

解：（1）在图6中，因为AB=BC=1，AD=2，E是AD的中点，∠BAD=，所以BE⊥AC，BE∥CD.即在图7中，BE⊥OA1，BE⊥OC.又OA1∩OC=O，OA1⊂平面A1OC，OC⊂平面A1OC，从而BE⊥平面A1OC.又CD∥BE，所以CD⊥平面A1OC.

（2）由已知，平面A1BE⊥平面BCDE，AO⊂平面A1BE，平面A1BE∩平面BCDE=BE，所以A1O⊥平面BCDE.因为OC⊂平面BCDE，所以A1O⊥OC.

又由（1）知，BE⊥A1O，BE⊥OC，所以，以O为原点，OB，OC，OA1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，如图8所示.

因为A1B=A1E=BC=ED=1，BC∥ED，所以

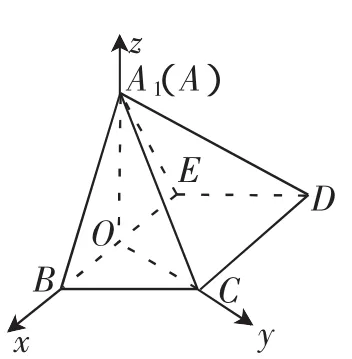
图8

设平面A1BC的法向量n1=（x1，y1，z1），平面A1CD的法向量n2=（x2，y2， z2），平面A1BC与平面A1CD的夹角为θ，则得，取=（1，1，1）.

从而 θ=|cos〈n1，n2〉|=，即平面A1BC与平面A1CD夹角的余弦值为

评注：折叠问题是常考常新的一类问题.本题以翻折变换为条件，充分考查考生的空间想像能力、推理论证能力与运算求解能力，以及向量的方法的运用等.若本题第（2）问改为求二面角B-A1C-D的余弦值，则需判断二面角B-A1C-D是否为锐角.