高三数学立体几何的复习建议和思考

☉江苏省海门实验学校 张 浩

高三数学立体几何的复习建议和思考

☉江苏省海门实验学校 张 浩

近几年的高考有逐步回归基础、回归课本、回归本质等的趋势.而目前这种卷子满天飞，大量盲目训练、重复训练、题型训练，使师生苦不堪言的复习过程，其实是注重操作，缺失本质、缺失思维的过程，高考过后，感到做了不少无用功，令人痛心.笔者结合立体几何备考过程中的复习措施，谈谈如何回归基础、回归课本、回归本质，期望展现平凡中的精彩，启发学生走出程式，走出模仿，提高数学解题能力.

一、回归考题，明确模型

由近几年的高考题容易发现，立体几何题型比较稳定.因此，关注考题的类型，是立体几何复习的关键.立体几何类命题以考查线面平行和垂直的判断与推理为主，一般地以选择题或填空题的形式考查概念性的知识与判定定理、性质定理的简单应用，以解答题的形式结合几何体的结构特征考查平行与垂直的判定、性质定理的综合运用，以及空间想象能力和逻辑思维能力.

例1如图1，在四棱锥ABCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=.

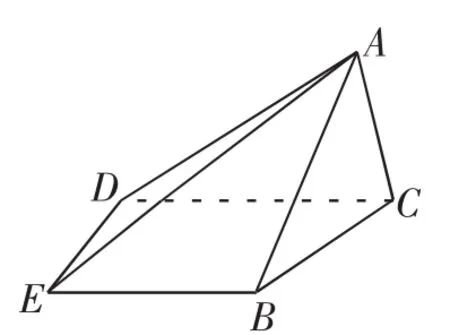
图1

（Ⅰ）证明：DE⊥平面ACD；

（Ⅱ）求二面角B-AD-E的大小.

分析：（Ⅰ）先在直角梯形BCDE中求出BC，即可利用勾股定理验证AC⊥BC，然后利用面面垂直的性质定理将已知平面ABC⊥平面BCDE转化为AC⊥平面BCDE，从而得到AC⊥DE，最后结合已知DE⊥DC即证得结论.（Ⅱ）方法1，根据（Ⅰ）中证的垂直关系作出二面角的平面角，然后求出其所在三角形的三边长，利用余弦定理求其值；方法2，根据（Ⅰ）中证的垂直关系建立空间直角坐标系，求出相应点的坐标及二面角的法向量，最后利用这两个法向量的夹角表示所求的二面角即可.

解：（Ⅰ）在直角梯形BCDE中，由DE=BE=1，CD＝2，得BD＝BC＝.由AC＝，AB=2，得AB2=AC2+BC2，即AC⊥BC.又平面ABC⊥平面BCDE，从而AC⊥平面BCDE.所以AC⊥DE，由DE⊥DC，从而DE⊥平面ACD.

（Ⅱ）方法1：作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AE交于点G，连接BG.由（Ⅰ）知，DE⊥AD，则FG⊥AD.所以∠BFG是二面角B-AD-E的平面角.在直角梯形BCDE中，由CD2=BC2+BD2，得BD⊥BC.

又平面ABC⊥平面BCDE，得BD⊥平面ABC，从而BD⊥AB.

由AC⊥平面BCDE，得AC⊥CD.

在△ABE，△ABG中，利用余弦定理分别可得

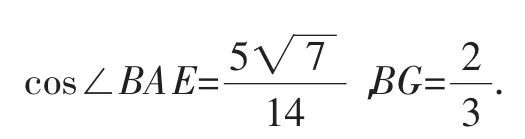
6

图2

方法2：以D为原点，分别以射线DE，DC为x，y的正半轴，建立空间直角坐标系D-xyz，如图2所示.由题意知，D（0，0，0），E（1，0，0），C（0，2，0），A（0，2，），B（1，1，0）.

设平面ADE的法向量为m= （x1，y1，z1），平面ABD的法向量为n=（x2，y2，z2），

点评：本题考查了空间位置关系证明以及求二面角.在解决空间距离与空间角问题时，有时可以采用几何法，有时可以采用向量法，可以结合题目的条件加以选择.而往往采用向量法解决问题时思路比较简单，是一种常用的方法，但是要会根据题意建立适当的坐标系.通过这道题的复习，对证明线面垂直和求二面角的大小有了明确的方法.

二、回归基础，系统梳理

高三一轮复习的展开，主要是基础知识的梳理，高效的一轮复习课是数学教师的不懈追求.例如某教师的上课流程如下：

环节1情景导入，引入复习

教师首先用多媒体课件以表格形式展示近几年来各省市高考数学试卷中有关立体几何中的空间角的相关试题类型及分值，然后展示分析考试大纲中相应的考试要求.

环节2回忆巩固，构建知识

多媒体课件上以问题串的形式提问学生并配图演示，以帮助学生完成对本节的知识梳理.

问题1：立体几何中学习的异面直线所成的角、直线和平面所成的角、二面角的概念是什么？

问题2：异面直线所成的角、直线和平面所成的角、二面角的范围是什么？

问题3：两条异面直线所成的角是它们方向向量的夹角吗？

问题4：直线和平面所成的角是直线的方向向量和平面的法向量的夹角吗？

问题5：二面角是两个平面的法向量的夹角吗？

问题6：如何用式子来说明三种角与向量夹角的关系？

教师引导学生将所求的角与向量夹角建立联系并通过向量计算来解决立体几何中的空间角问题.

环节3典例剖析，考点突破

例2如图3，直角梯形OABC中，OA∥BC，∠AOC=90°，SO⊥平面OABC，且OS=OC=BC=1，OA=2.

（Ⅰ）求异面直线SA和OB所成的角的余弦值；

图3

（Ⅱ）求OS与面SAB所成角的

正弦值；

（Ⅲ）求二面角B-AS-O的余弦值.

教师分析并在黑板上板书解题过程，示范立体几何中空间角问题的常规解法和解题规范步骤，规范学生的解题步骤和过程.

环节4合作交流，互动探究

（1）自主练习

如图4，已知长方体AC1中，棱AB= BC=1，棱BB1=2，点E是CC1的中点.

（Ⅰ）求BE和A1C所成角的正弦值；

图4

（Ⅱ）求ED与平面A1B1C所成角的正弦值；

（Ⅲ）求二面角E-BD-C的余弦值.

学生练习，利用多媒体投影仪投影部分学生的解题过程，进一步规范学生的解题过程.

（2）变式提升（学生自主编制试题）

学生练习后，在提前将学生分组的前提下，以练习中的长方体为背景，由一组编制试题（三类空间角的问题），另一组解答.因为在练习环节已经建好坐标系，找好了各点的坐标.因此时间是允许的.这样可以激发学生的学习积极性，培养学生自主探索、动手实践和合作交流的能力，真正实现“知识的深化”和“能力的活化”.

环节5完整体系，思维升华

问题7：通过学习，体会向量法求空间角的一般步骤.

问题8：通过本节的学习，你有什么体会？（引导学生分析、综合、提升）

（1）空间问题平面化：立体几何平面化与空间向量平面化；

（2）立体几何向量化：解题的关键是找出直线的方向向量与平面的法向量，通过两条射线所成的角解决所求角的计算，转化为平面角的计算；

（3）向量问题坐标化：通过找点、向量的坐标的运算将平面角用坐标法求出.

本课例中的几个环节通过问题串的形式给出概念和公式给出基础知识，情形正如章建跃博士所言：“大量数学教师在课堂上没有抓住数学概念的核心进行教学，学生经常在没有对数学概念和思想方法有基本了解的情况下就盲目进行大运动量的解题操练，导致教学缺乏必要的根基，教学活动不得要领.学生花费大量时间学数学，完成了无数次解题训练，但他们的数学基础仍非常脆弱.”在数学一轮复习中，以呈现基础知识为主，帮助学生从整体上真正理解概念，掌握数学的基础知识，完成对知识的重组，逐个击破知识点.

三、回归课本，追溯本源

在立体几何复习中，如能很好地抓住课本上的一些基本、典型的关系，既可简化求解过程，提高复习效率，又可培养全面深刻、灵活多变的思维能力.

问题：在Rt△ABC中，两直角边分别为a，b，设h为斜边上的高，则=+.类比并论证：三棱锥S-ABC的三条侧棱SA，SB，SC两两垂直，且长分别为a，b，c，设棱锥底面上的高为h，则a，b，c，h之间有关_______.

课本习题：S是△ABC所在平面外一点，SA⊥SB，SB⊥SC，SC⊥SA，SH⊥平面ABC于H.求证H是△ABC的垂心.

解析：如图5，作SH⊥平面ABC，垂足为H，连结AH并延长交BC于G，连结SG.由习题的证明过程可知，BC⊥平面SAG，BC⊥SG.设SG的长为x，则在Rt△CSB中

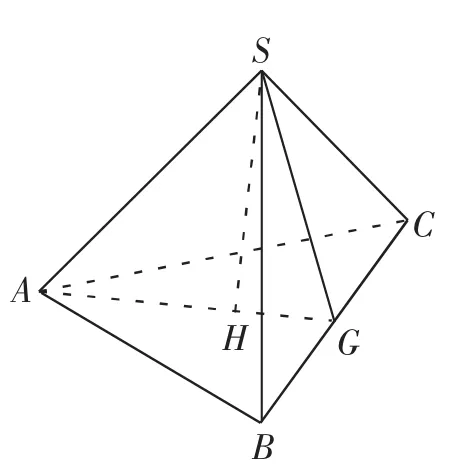
图5

立体几何的一个重要作用是培养空间想象能力，向量引入计算和证明，很好地体现了转化与化归思想，使问题的解决灵活多样，但课本反映的基本空间关系不可丢.高三的复习要引导学生利用基础知识、基本技巧逐步掌握解题过程的一般规律，学习分析方法，提高分析能力，切不可变成模仿训练，重复训练.

总之，高三数学复习中，学生对数学思想方法的理解和掌握必须依靠典型的问题来体现，因此在高三一轮复习教学中，教师要精选例题，应精选那些最能体现本质的思想方法的例题和练习，用它们来支撑和验证本质的思想方法和通性通法确实是最有效的解题策略.

另外，我们提倡讲授式教学和探究式教学的有效整合.我们不能“满堂灌”，也不能将“讲授式”拒于课堂之外，应根据不同问题的特点，选取恰当的教学方法.该教师讲授的，教者要滔滔不绝；该学生探究的，教师要积极创设情境，充分发挥学生学习的主动性，通过师生互动、生生互动，让学生真正参与、亲身经历教学过程，使学生的学习过程成为在教师引导下的“再创造”过程.