基于递归分析的生物质与惰性颗粒混合流动压差脉动信号混沌分析

王泽宇，仲兆平，王肖祎，赵凯

（东南大学 能源与环境学院，能源热转换及其过程测控教育部重点实验室，江苏 南京，210096）

基于递归分析的生物质与惰性颗粒混合流动压差脉动信号混沌分析

王泽宇，仲兆平，王肖祎，赵凯

（东南大学 能源与环境学院，能源热转换及其过程测控教育部重点实验室，江苏 南京，210096）

将递归图及其定量分析方法应用于双组分流化床流动混沌分析中，对大颗粒生物质（当量直径为5 mm，密度为350 kg/m3）与石英砂（直径为0.4 mm，密度为2 700 kg/m3）在流化床内混合流动的压差脉动信号进行持续10 s的采样提取，并对其进行递归图和递归定量分析。研究结果表明：在鼓泡流状态下生物质颗粒的存在降低床内流动的随机性，增强系统的平稳性。系统的确定性和周期性随着气速的增加而增强。而当气速小于最小流化风速时，床内流动接近固定床状态，递归特征值的变化规律不明显，系统的随机性较强。

压差脉动；递归定量分析；递归图；生物质；流化床；多相流

生物质在流化床内的热解气化是一种良好的生物质能源利用技术。但由于生物质密度小、形状不规则、颗粒尺寸较大等特性，生物质在流化床内难以稳定流动，易出现沟流或腾涌现象，同常将惰性颗粒如石英砂与生物质混合，这样不仅可以增强生物质的流化质量，还可以强化传热，提高热解效率。递归图分析方法通过相空间重构法将高维的相空间轨迹的递归关系直观地呈现在二维递归图上，在医疗、机械、信息等领域有着广泛应用［1-2］。对于非线性动力系统，递归图可以定性的揭示较短的时间序列的递归关系，从而给出系统的周期性，确定性，结构复杂性等评价结果。ECKMANN等［3］最初使用递归图（recurrence plot，RP）对Lorenz系统进行定性的分析，并指出递归分析是一种简便直观且有效的非线性动力系统分析方法。DONG等［4］将递归分析与小波分析方法结合研究了油水两相流流型复杂动力学特性，较好地揭示了两相流相界面的运动变化情况。MARWAN等［5］使用相干递归图（cross recurrence plots，CRP）分析了不同时间序列的2个非线性信号。气固流化床压差脉动信号主要由床内气泡和颗粒流动引起，可以很好地揭示床内的气泡特性、颗粒特性和反应器的几何特性等。由于流化床内气固两相流过程十分复杂，产生的压差脉动信号非线性和随机性很大［6］。STRINGER等［7-8］也都证明了单组分细颗粒流化床流动的压力脉动信号具有混沌与分形的特性。王春华等［9］通过对单组分流化床压力脉动信号的递归图分析，提取了不同床型下的递归图特征量，从而对流化床的不同流型进行辨识。王肖祎等［10］对成型生物质与石英砂在流化床内流动压差脉动信号进行了递归分析，得出鼓泡床状态与腾涌状态下成型生物质质量分数和气速的变化对流动混沌特性的影响。对于未成型的生物质颗粒与石英砂在流化床内的流动的混沌特性仍鲜有研究，本文作者通过对流化床床层的压差脉动信号进行递归图和递归定量分析，研究气速和生物质质量分数的变化对系统的确定性、周期性的影响，从而探索了未成型生物质与石英砂双组分在流化床中的混沌特性，这对生物质颗粒与惰性颗粒混合流动机理以及生物质颗粒流化床内热解和气化过程的研究具有重要意义。

1 递归分析方法

1.1 递归图

1个混沌动力系统的某些状态往往在某个特定的时间段具有一定的相似性，这种相似性就称为系统的递归性。将1个一维的时间u（t）离散化表示为ui，其中t=iΔt，Δt为采样时间间隔。按一定的嵌入维数（m）［11］和延迟时间（τ）［8］进行相空间重构后得到

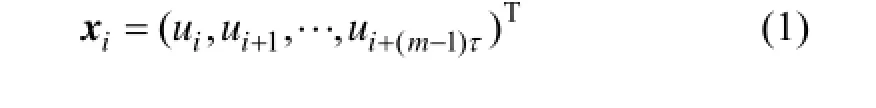
为使重构后的相空间轨迹与原始空间轨迹等价，需满足m＞2d+1，d为相空间吸引子维数。

定义递归矩阵

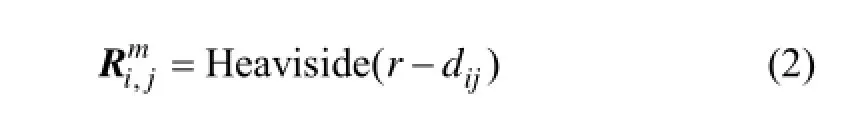
其中：

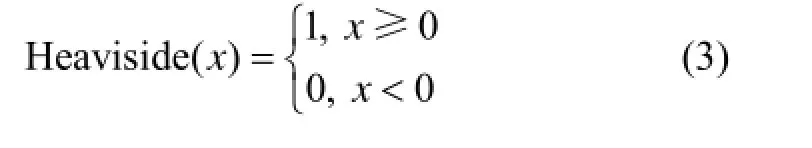
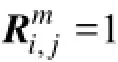
周期信号的递归图如图1所示，为1个正弦信号的递归图，在图形上表现为棋盘状，大量递归点在对角线和垂直于对角线方向上排列整齐有序。

图1 周期信号递归图Fig.1 Recurrence plot of periodic signal

Lorenz吸引子是一种典型的混沌系统，它是由洛伦兹（Lorenz）［12］在1963年提出的极端简化的天气预报模型，其微分方程如下：

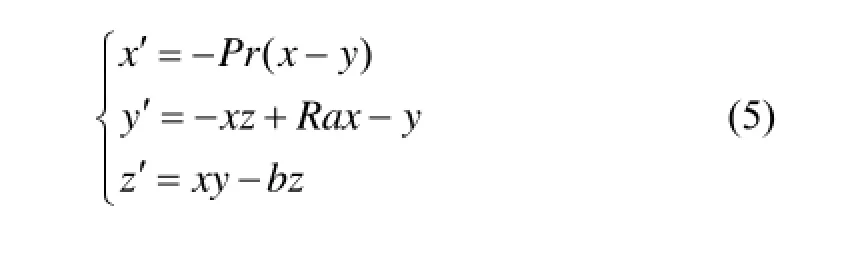
式（5）是一组不显含时间的常微分方程组，其中Pr为普朗特（Prandtl）数；Ra为瑞利（Rayleigh）数；b为正实数。方程中的非线性相使得系统各部分相互作用，所以，Lorenz吸引子是1个混沌动力系统，选取Pr=10，Ra=28，b=8/3，其相空间轨迹如图2所示。

图2 Lorenz吸引子相空间轨迹Fig.2 Phase space trajectory of Lorenz attractor

对其进行相空间重构，采用C-C算法计算延迟时间τ［13］，采用伪最邻近法（false nearest neighbors， FNN）计算嵌入维数m［14］，其递归图如图3所示。

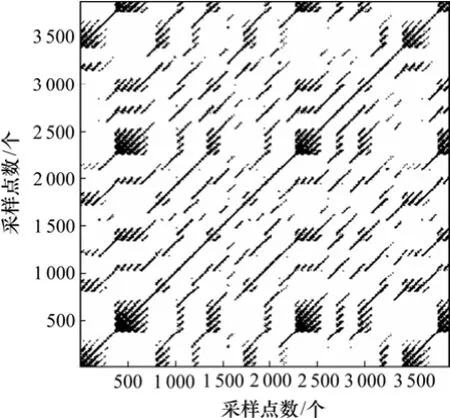
图3 Lorenz吸引子递归图Fig.3 Recurrence plot of Lorenz attractor

观察Lorenz系统递归图可以得出3种基本形式的微观纹理特征：1） 孤立点，这主要是系统的不稳定性引起的；2） 平行于主对角线方向的线段，表示系相空间轨迹在某个时间段持续的逼近，反映了系统的确定性和稳定性；3） 垂直或水平的线段，表示系统在某一时刻出现停滞或缓慢变化的状态。Lorenz系统的递归图既具有一定数量长短不一的沿对角线方向的线段，也具有一定数量的孤立点。还有一些呈块状分布的区域，这是代表系统的突变结构。

1.2 递归定量分析

递归图分析能够直观地反映混沌系统的相空间结构，但只能定性地研究时间序列的复杂性和可预测性［15］。为此，ZBILUT等［16-17］提出了基于递归图小尺度结构的递归定量分析方法。

递归定量分析针对信号递归图的局部结构细节进行分析（主要是对角线方向的分析），并从中提取特征量，通过特征量量化系统的各项指标。递归定量分析所选择的特征量有以下几种。

1） 确定性（QDET）。

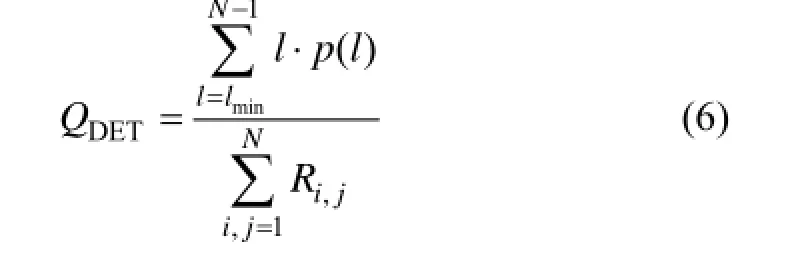
式中：p（l）是长度为l的线段数，lmin一般选择不小于2的整数； QDET表示沿对角线方向的递归点占总递归点的比例，其值越大说明系统确定性越强［12］。

2） 平均对角线长度（QL）。

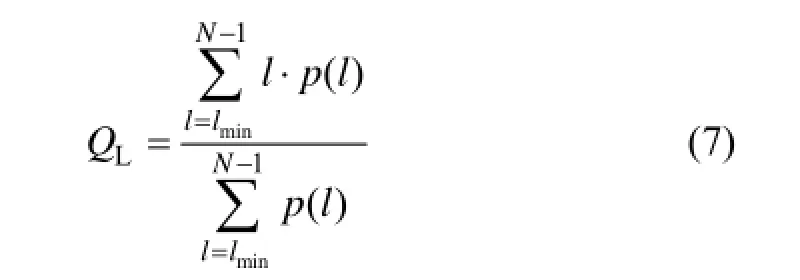
表示发生递归现象的平均持续时间，即系统的平均周期［12］。

3） 熵（QENTR）。

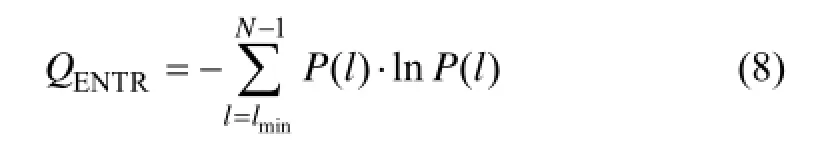
式中：（）P l是长度为l的线段数占总线段数的比例，

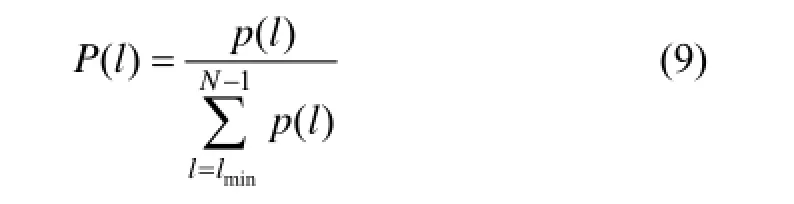
熵即对角线方向线段频次分布的香农熵，反映了系统的确定性结构的复杂性［18］。

4） 层流率（QLAM）。）

式中：

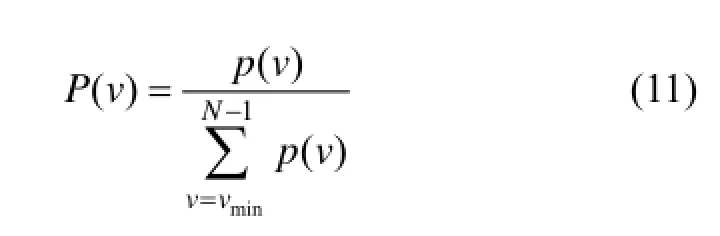
层流率越大说明系统间歇性越大［13］。

2 实验方案

本实验以玉米芯颗粒和石英砂为床料，玉米芯颗粒为玉米芯经由破碎机破碎后自然风干所得，床料物理特性如表1所示。实验装置由流化床主体、供风系统、数据采集系统组成。如图4所示，流化床主体由有机玻璃制成，布风板的长×宽为120 mm×32 mm，其上错列分布着126个直径为1 mm的圆孔，开孔率为2.6%，以使流化风均匀进入床内。布风板上覆盖着一层孔径为0.25 mm的筛网，以防止细颗粒石英砂落入布风板造成布风板堵塞。

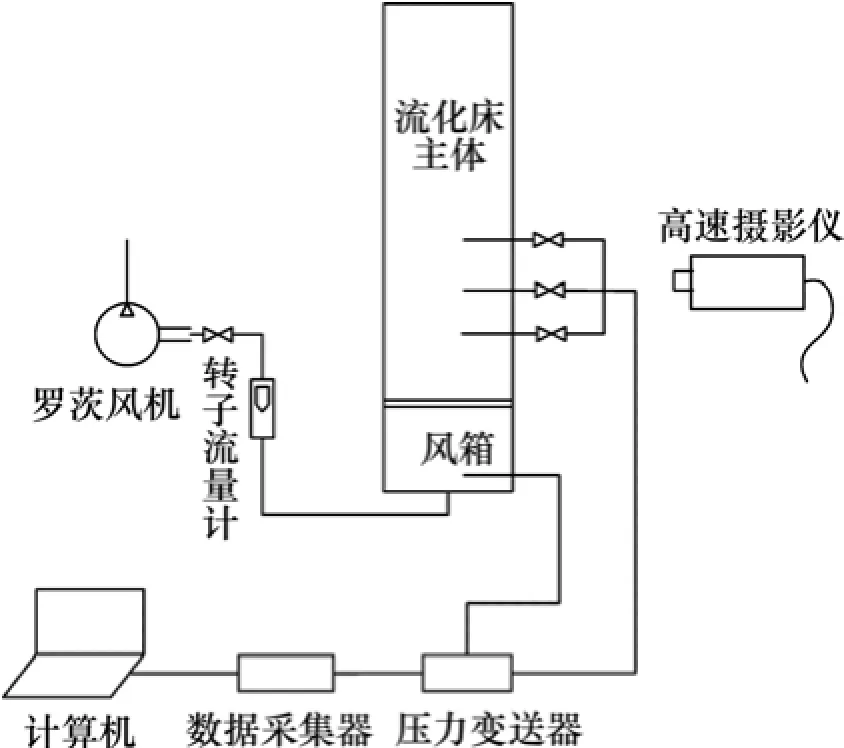
图4 实验装置系统图Fig.4 Schematic diagram of experimental setup

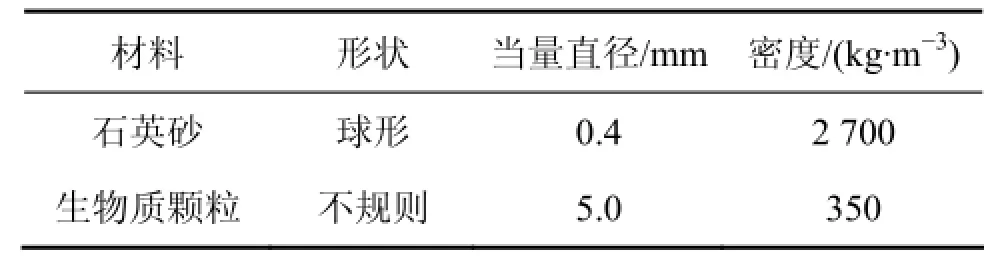
表1 实验材料物理特性Table 1 Physical properties of materials

本次实验使用罗茨风机（型号：L21LD；升压：29.4 kPa）为流化床提供流化风。采用转子流量计控制风速。测压点分别布置在距布风板200，300和400 mm的位置上，用来测量不同床高下的压差脉动信号。压力变动器（型号：KMSSTO；量程：0～35 kPa）与USB数据采集器（RBH8251-13）用来采集床内的压差脉动信号，采样频率为100 Hz，连续采集10 s以上。高速摄影仪（photron SA4）用来采集床内流动图像，以观察床料和气泡的运动状态。最大记录速度为12 500幅/s。本次记录速度为1 000幅/s，图像像素为1 024×512。本实验选取工况：静止床高H=150 mm、表观气速v为0.30～2.17 m/s，玉米芯质量分数w分别为4%，8%和16%。

3 数据分析

3.1 最小流化风速

图5所示为不同生物质质量分数w时平均压差Δp随气速的变化曲线图，由图5可知：随着生物质质量分数的增加，平均压差逐渐减小，其中，w=4%和w=8%的混合流动与单组分石英砂的流动相差不大，而当w=16%时平均压差下降明显。

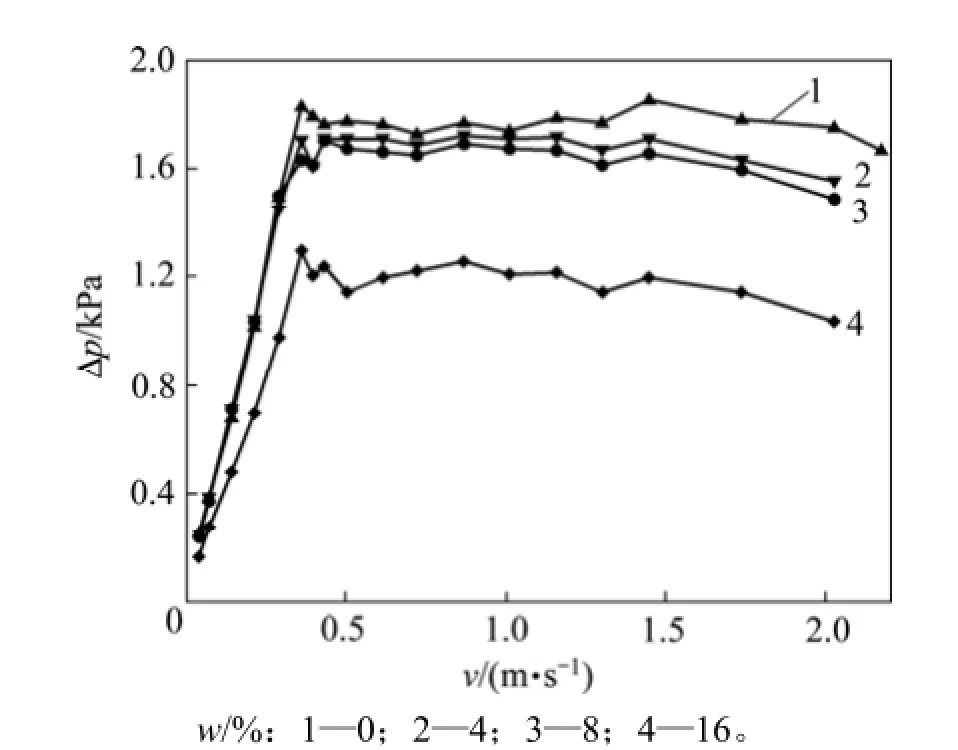
图5 不同生物质质量分数w时平均压差随气速的变化Fig.5 Change of average pressure with gas velocity at different biomass mass fractions

采用降压法测得不同生物质质量分数的最低流化风速，根据图5可以得出不同生物质质量分数下的最低流化风速相差不大，约为0.45 m/s。

3.2 递归图分析

图6所示为当v=0.87 m/s时床内流动状态。由图6可知：此床内流动处于典型的鼓泡状态，气泡数比较大且气固分界面明显。随着生物质质量分数的增加，压差脉动信号的频率逐渐减小，平均压差减小。当v=1.45 m/s时，床内湍动加剧（图7），气泡边缘变得模糊，流动状态出现湍动流态化状态。与小气速工况（图6）相似，生物质质量分数的增加同样降低了平均压差和振动频率。

图8和图9所示分别为v=0.87 m/s和v=1.45 m/s时床内压力脉动其递归图。由图8（a）和9（a）可知：单组分的石英砂颗粒在流化床内的流动递归图总体上具有网格状结构，说明系统具有较强的周期性。递归图中出现较多的块状、水平和垂直的线段，说明系统具有较强的间歇性和突变性［19］，这是由于床内的石英砂颗粒较细且形状均一，易形成较大的气泡，气泡的生长和破裂会产生较大的压力脉动。

图6 v=0.87 m/s时床内流动状态Fig.6 Flow state of bed at v=0.87 m/s

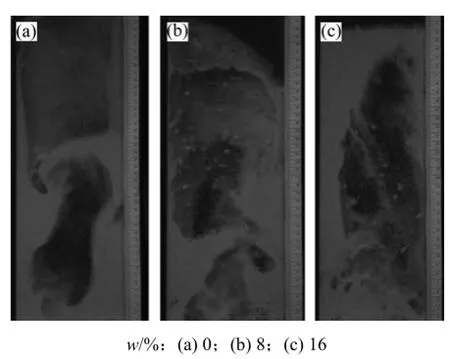
图7 v=1.45 m/s时床内流动状态Fig.7 Flow state of bed at v=1.45 m/s

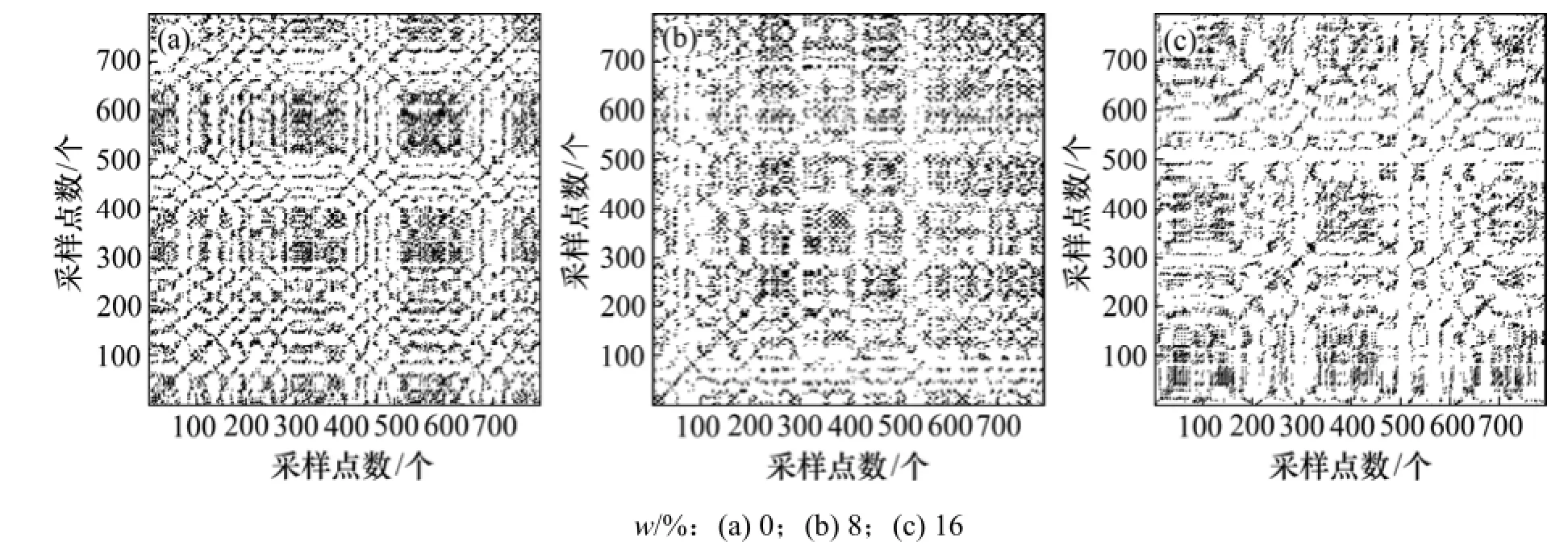
图8 v=0.87 m/s时压力脉动递归图Fig.8 RP of pressure fluctuation at v=0.87 m/s

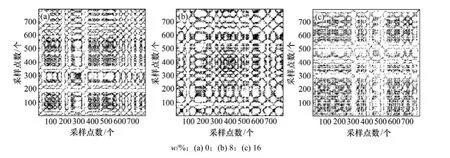
图9 v=1.45 m/s时压力脉动递归图Fig.9 RP of pressure fluctuation at v=1.45 m/s

当玉米芯颗粒质量分数增加时，流动递归图（图8（b）和（c））产生递归的点较单组分石英砂的逐渐减少，块状结构逐渐消失，但仍存在较多的对角线方向的短线段，说明玉米芯颗粒的存在使得系统的递归性和突变性减弱，但仍然存在较强的混沌特性。这主要是因为在混合流动的时候气泡尺寸会随着高度的增加而增大，同时向四周排挤周围的颗粒，但由于玉米芯颗粒在形状、体积和密度上与石英砂颗粒相差很大，被抬升的玉米芯颗粒会回落到气泡中（图7（b）和7（c）），从而破坏气泡，使得气泡分裂成更小的气泡，床内的压差脉动也随之趋于平缓。随着气速的增加，床内的流动状态仍然处于鼓泡状态，并没有因为气速太大或太小产生腾涌和固定床状态，具有一定的可比性。通过对比可看出v=1.45 m/s时的递归图块状结构跟明显，流动具有较强的突变性。这主要由于气速的增加会使得气泡的尺寸增大。

3.3 递归定量分析

递归图分析方法可以直观地看出生物质与石英砂在流化床内流动混沌系统的周期性和突变性。为了更进一步研究不同工况下系统递归图细微结构的变化规律，则需对压力脉动信号的递归图提取特征参数进行递归定量分析。

3.3.1 确定性（QDET）

图10（a）所示为不同生物质质量分数递归特征量QDET随气速变化情况。在固定床状态（v＜0.4 m/s），气体不能汇聚成气泡而从床料之间的缝隙中穿过，床料处于轻微的震动状态。这就使得压力脉动信号接近于随机状态，当床内流动状态从固定床向鼓泡流转变的过程中（0.4＜v＜0.8 m/s），床内逐渐产生小气泡，气泡尺寸随着气速的继续加大而加大，从而增大了确定性。同时，气体的紊流加剧，又降低了系统的确定性。所以系统的确定性表现为先急剧上升再急剧下降。当气速继续加大，床体流动状态完全发展为鼓泡流，总体来看此时QDET在鼓泡阶段随着气速变化较为平缓。当生物质质量分数增加时，QDET是逐渐下降的，这说明生物质的存在降低了系统的确定性。

3.3.2 平均对角线长度（QL）

图10（b）所示为不同生物质质量分数递归特征量QL随气速变化情况。单组分石英砂QL随着气速的增长呈M型趋势，与确定性相似。当v＜0.8 m/s时，系统的周期性同时受气泡尺寸和气体紊流状态的影响，表现为先增后减。当v＞0.8 m/s时，纯石英砂流动有向湍流流态化发展的趋势，气泡与颗粒混合剧烈，所以QL有减小的趋势。而随着生物质质量分数的增加，床内气泡受生物质的扰动增大，平均对角线长度减小，QL曲线的M型趋势减弱。这表明系统的平均周期随着生物质质量分数的增加而降低。气速对平均周期的影响也随着生物质质量分数的增加而减弱。这是由于生物质的存在加速了气泡破碎，使得床内气泡尺寸减小，并且分布更加均匀。

3.3.3 层流率（QLAM）

图10（c）所示为不同生物质质量分数时递归特征量 QLAM随气速变化情况。系统的层流率随气速的增加先下降再上升。当床内为固定床时，不同生物质质量分数的 QLAM相接近，且随气速的增大为减小。当床内处于鼓泡流动状态时，QLAM随气速增加而增加，同时生物质质量分数w的增加使得QLAM降低，这与递归图分析结果相吻合。当v＞0.8 m/s时，w=8%的系统QLAM与单组分石英砂相近。而当w=16%时，系统的 QLAM相对较低，这表明较高的生物质质量分数使得气泡尺寸分布相对均匀，增加了系统的连续性。

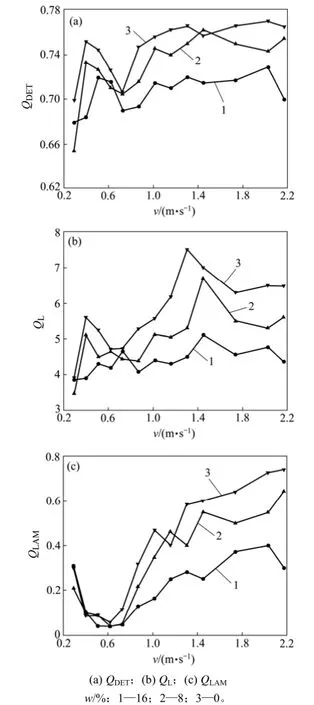
图10 不同生物质质量分数时递归特征量随气速的变化Fig.10 Change of recurrence characteristic values with gas velocities at different biomass mass fractions

4 结论

1） 递归图通过相空间重构的方法可以直观定性地将非线性动力系统的混沌特性描述在二维平面上，通过特征量可以定量分析动力系统的递归特性，对于混沌信号的分析是一种较好的研究方法。对流化床的压力脉动信号的递归分析可知生物质与石英砂双组分在流化床内混合流动具有较强的混沌特性。

2） 气速的增加会使得处于鼓泡床状态的流动混沌特性增强。此时递归图平均对角线长度和香农熵在单组分石英砂的工况下变化较剧烈，大颗粒生物质的存在会扰乱气泡的运动状态，致使大尺寸气泡破裂生成更小尺寸的气泡，从而使系统能量耗散加剧，所以，生物质质量分数的增加使得系统趋于平缓，降低了系统的确定性、周期性和间歇性。

3） 当表观气速小于0.8 m/s时，床内接近于固定床状态，气体主要通过物料的缝隙流出床体，且几乎没有大尺度的气泡出现，各递归特征值的变化规律不明显，系统的递归特性较弱，很难通过递归图反映出生物质质量分数的变化对流动的影响。

［1］ BELAIRE-FRANCH J， CONTRERAS D， TORDERA-LLEDÓ L. Assessing nonlinear structures in real exchange rates using recurrence plot strategies［J］. Physica D： Nonlinear Phenomena，2002， 171（4）： 249-264.

［2］ DU B X， LIU Y， LIU H J， et al. Recurrent plot analysis of leakage current for monitoring outdoor insulator performance［J］. IEEE Transactions on Dielectrics and Electrical Insulation， 2009，16（1）： 139-146.

［3］ ECKMANN J P， KAMPHORST S O， RUELLE D. Recurrence plots of dynamical systems［J］. Europhysics Letters， 1987， 4（9）：973.

［4］ DONG Fang， JING Ningde， ZONG Yanbo， et al. Multi-scale recurrence quantification analysis of the dynamic characteristics of two phase flow pattern［J］. 2008， 57（10）： 6145-6154.

［5］ JIN Ningde， ZHENG Guibo， DONG Fang， et al. Application of chaotic recurrence plot analysis to identification of oil/water two-phase flow patterns［M］. Berlin， Heidelberg： Springer， 2006：1213-1216.

［6］ MARWAN N， KURTHS J. Nonlinear analysis of bivariate data with cross recurrence plots［J］. Physics Letters A， 2002， 302（5）：299-307.

［7］ STRINGER J. Is a fluidized bed a chaotic dynamic system［C］// Proceedings of the 10th International Conference on Fluidized Bed Combustion. San Francisco， 1989： 265-272.

［8］ ZHAO Guibing， CHEN Jizhong， YANG Yongrong. Study on the nature of pressure signals in a bubbling fluidized bed［J］. Journal of Zhejiang University： Science， 2002， 3（4）： 435-439.

［9］ 王春华， 仲兆平， 李睿， 等. 气-固流化床压力脉动递归图分析［J］. 化工学报， 2010， 61（3）： 557-564. WANG Chunhua， ZHONG Zhaoping， LI Rui， et al. Recurrence plots analysis of pressure fluctuation in gas-solids fluidized bed［J］. CIESC Journal， 2010， 61（3）： 557-564.

［10］ 王肖祎， 仲兆平， 王春华. 流化床内生物质石英砂双组分混合流动混沌递归分析［J］. 化工学报， 2014， 65（3）： 813-819. WANG Xiaoyi， ZHONG Zhaoping， WANG Chunhua. Chaotic recurrence analysis of two-component flow of mixed biomass particles and quartz sands in fluidized-bed［J］. CIESC Journal，2014， 65（3）： 813-819.

［11］ 刘树勇， 朱石坚， 俞翔. 确定相空间重构嵌入维数的研究［J］.哈尔滨工程大学学报， 2008， 29（4）： 374-381. LIU Shuyong， ZHU Shijian， YU Xiang. Determinating the embedding dimension in phase space reconstruction［J］. Journal of Harbin Engineering University， 2008， 29（4）： 374-381.

［12］ LORENZ E N. Deterministic nonperiodic flow［J］. Journal of the Atmospheric Sciences， 1963， 20（2）： 130-141.

［13］ BROOMHEAD D S， KING G P. Extracting qualitative dynamics from experimental data［J］. Physica D： Nonlinear Phenomena，1986， 20（2）： 217-236.

［14］ PACKARD N H， CRUTCHFIELD J P， FARMER J D， et al. Geometry from a time series［J］. Physical Review Letters， 1980，45（9）： 712.

［15］ 吕勇， 徐金梧， 李友荣. 递归图和近似熵在设备故障信号复杂度分析中的应用［J］. 机械强度， 2006， 28（3）： 317-321. LÜ Yong， XU Jinwu， LI Yourong. Application of recurrence plot and approximate entropy on complexity analysis of machinery fault signal［J］. Journal of Mechanical， 2006， 28（3）： 317-321.

［16］ ZBILUT J P， WEBBER C L Jr. Embeddings and delays as derived from quantification of recurrence plots［J］. Physics Letters A， 1992， 171（3）： 199-203.

［17］ MARWAN N， WESSEL N， MEYERFELDT U， et al. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data［J］. Physical Review E，2002， 66（2）： 026702.

［18］ WEBBER C L， ZBILUT J P. Dynamical assessment of physiological systems and states using recurrence plot strategies［J］. Journal of Applied Physiology， 1994， 76（2）：965-973.

［19］ HONG W， ZHOU Y， LIU Y. Chaotic recurrence characteristics analysis of differential pressure fluctuating signal across tube bundles［J］. Proceedings of the CSEE， 2011， 31（23）： 74-78.

（编辑 杨幼平）

Chaotic analysis of pressure fluctuation of quartz sands flow mixed with biomass particles based on recurrence analysis

WANG Zeyu， ZHONG Zhaoping， WANG Xiaoyi， ZHAO Kai

（Key Laboratory of Energy Thermal Conversion and Control of the Ministry of Education， School of Energy and Environment， Southeast University， Nanjing 210096， China）

The recurrence plot （RP） and recurrence quantification analysis （RQA） were used in the chaotic analysis of two-component flow in fluidized-bed. Pressure fluctuation signals generated by the fluidized bed flow were sampled for 10 min， and were analyzed by RP and RQA. The materials of the research were the mixture of biomass （equivalent diameter： 5 mm， density： 350 kg/m3） and silica sands （diameter： 0.4 mm， density： 2 700 kg/m3）. The results show that the existence of biomass decreases the chaos properties but improves the reliability of the dynamic system in the fluidized bed on the bubbling conditions. However， there is not obvious regularity on the characteristic value when the velocity is below the minimum fluidizing gas velocity and the flow pattern in the bed is close to fixed bed， which means a strong randomness of the system.

pressure fluctuation； recurrence quantification analysis； recurrence plot； biomass； fluidized-bed； multiphase flow

TQ051

A

1672-7207（2016）05-1767-07

10.11817/j.issn.1672-7207.2016.05.041

2015-05-27；

2015-07-22

国家自然科学基金资助项目（51276040）；国家重点基础研究发展计划（973计划）项目（2013CB228106） （Project（51276040）supported by the National Natural Science Foundation of China； Project（2013CB228106） supported by the National Basic Research Development Program （973 Program） of China）

仲兆平，博士，教授，从事废弃物资源化和可再生能源技术、大气污染控制等研究；E-mail： zzhong@seu.edu.cn