加强思维训练提升思维品质

保春燕

摘要：数学教育的本质就是发展学生的思维，数学教学中的思维训练，是通过教师、学生、教材三者的多维互动，实现思维品质的有效提升。在课堂教学中，教师要把思维训练贯穿于数学课堂教学的各个环节：创设情境，激发思维动机：主动探索，促进思维发展；总结深化，提升思维品质。力求让课堂成为思维训练的力场，促使学生的数学思维在这一过程中获得最大的发展！

关键词：思维动机；思维的深刻性；灵活性；独创性；思维品质

加里宁说过“数学是思维的体操”。思维是事物的本质属性和内部规律性在人脑中的反映，它是智力的核心。数学教育的本质就是发展学生的思维。因此，在课堂教学中，教师要把思维训练贯穿于数学课堂教学的各个方面，力求让课堂成为思维训练的力场。特级教师张齐华在《确定位置》一课的教学中给我们提供了具体的路径。

一、创设情境，激发思维动机

动机是人们“因需要而产生的一种心理反应”，它是人们行为活动的内动力。因此，激发学生思维的动机，是培养学生思维力的关键因素。教师必须善于利用学生的好奇、好胜等心理特点，给学生创设学习数学的有效情境，从而为学生主动参与学习、积极进行思维提供最佳的心理准备。

课始，张老师以寻找最帅的儿子为切入点，在出示了一系列的照片后，学生哗然，无法确定哪一个是张老师的儿子。接着，教者给出一组数对（4，2），学生们在激烈探讨后，出现了不同的答案：有先从上到下，再从左至右数第4行第2列的；有先从上到下，再从右至左数第4行第2列的；有先从左至右，再从上到下数第4列第2行的；先从右至左，再从上到下数第4列第2行的。最终锁定4个头像，教者调侃：没有这么多儿子，这里只有一个是我的。质疑：到底哪一个是真的呢？问题出现在哪里？一语惊醒梦中人，生齐：老师，你没说清楚？（4，2）中哪个指的是行，哪个指的是列？是从哪边（即从什么方向）开始数的？

创设情境问题是思维的起点。有问题才会有思考，有思考才会有真正的思维活动。巧妙恰当地提出问题，创设良好的思维情境，能够迅速集中学生注意力，激发学生的兴趣和求知欲。张齐华老师的有效有意导入，使得学生们兴趣盎然，快乐地踏上了思维之旅。

二、主动探索，促进思维发展

教学中，不仅要注意学生是否找出规律，更应注意学生是否进行思考。创设情境后，放手让学生用自己喜欢的学习方法进行学习，变教师的“教”为“导”、学生的“学”为“探”，从而引导学生自主探索合作交流，在此过程中培养学生独立分析问题的能力，促进思维的发展。

1.沟通内在联系.培养思维的深刻性

思维的深刻性是指思维活动的抽象程度和逻辑水平，它集中表现在善于深入地思考问题，能从复杂的表面现象中，发现和抓住事物的规律和本质。因此沟通知识间的内在联系，是培养思维深刻性的主要手段。

学起于思，思源于疑。朱熹说：“学贵有疑，小疑则小进，大疑则大进。”张老师对于学生的疑问，并没有给出直接的答案。而是说：“我儿子最铁的哥们的位置是（2，1）。”（在屏幕上圈出头像）此时学生思绪万千，想说的话特别多。张老师趁机让学生进行小组讨论，恰到好处。

学生们七嘴八舌地交流着自己的想法，张老师适时抛出：“现在你能找着我儿子了吗？”生齐：“能！”

“哪一个？”

“第4列第2行。”

“帅吗？”

“帅！”学生开心地大笑。

“说说你是怎么找着的？”

生1：那个最铁的哥们的位置（2，1），就是左数第2列最下面第1行。所以，（4，2）就是第4列第2行。

“还有不同意见吗？你们都同意他的说法吗？”

生齐：“同意！” “恭喜你，答对了。”微笑示意其坐下。“今天我们一起来研究‘用数对确定位置’。”

接着给出几个数对判断位置。

在让学生进行自主探索时，若遇到学生一筹莫展，不知从何下手的时候，张老师没有通过直接的传授，而是借助知识间的内在联系，以巧妙的疏导、殷勤的期待、热情的鼓励，引导学生深入思考，在思考中掌握知识，在掌握知识中发展自己的思维能力。

2.开拓思维空间.培养思维的灵活性

思维的灵活性指的是善于从不同角度和不同方面进行分析思考，学生思路开阔，能灵活变换某种因素，调整思路，从一个思路到另一个思路，从新角度去思考，善于巧妙地转变思维方向，随机应变，产生适合时宜的办法。

照片中的数对迎刃而解之后，张老师联系实际：“你觉得你在教室里所处的位置，能用数对来表示吗？”

生点头大声应允：“可以。”

“第1列第1行在哪里？”（学生举手示意）

有两位学生同时举手。（师皱眉）

启发引导，师生明确：应站在讲台的角度来看，第1列第1行的位置。

请出班长、副班长、体育委员，分别说出其所处的位置。

跟同桌说说自己所处的位置，并记住自己的位置，进行听数对起立的游戏。

游戏步骤：

①师依次由慢渐快地报出：（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），听到自己数对的学生一一起立，学生站成一列。

②请学生报数对，听到自己数对的同学起立。（学生依照教者的形式报出数对）

（1，1），（2，1），（3，1），（4，1），（5，1），…，学生站成一行；

（1，1），（2，2），（3，3），（4，4），（5，5），…，学生站成一斜排；

（1，6），（2，5），（3，4），（4，3），（5，2），…，学生又站成另一斜排。

③师：都这样说成一行一列，已没什么新鲜感，下面谁来挑战：报一个数对就能站一列或一行或斜排？

生1报（2，0），没人站。

生2报（1，1-7），师含笑：打包出售了。没人理。

生3报（1，），师：这是数对吗？众生摇头。

生4报（3，x），师相机板书。（3，1），（3，2），（3，3）…位置的学生，依次在其他学生提醒声中缓缓起立。

师面对他们一一询问：你是（3，x）吗？第一位学生摇头，师示意其坐下，继而整列学生都被这一问题一一轰坐下。紧接着，师又面向他们一一再询问：x可以代表1吗？可以代表2吗？……刚刚被轰坐下的学生又一一站起。整个课堂充溢着快乐的思辨，学生的思路逐渐开阔起来，从具体的数字到用字母来代替数字，这不正是学生思维灵活性的体现吗？

3.提倡求异思维.培养思维的独创性

思维的独创性是指个体独立思考创造出新颖的有社会价值的智力品质，是人类思维的高级形态，是智力活动的独立创造水平。学生的独创性思维即善于探求新的途径和寻找新的方法去解决问题，提出自己独到的见解。在教学中要提倡求异思维，鼓励学生探究求新，激发学生在头脑中对已有知识进行“再加工”，以“调整、改组和充实”，创造性地寻找独特简洁的解法，培养思维的独创性。

“一石激起千层浪”。用字母表示数，把学生的思维又推向了另一个高起点。

张老师在拓展延伸环节中设置了这样两个问题：

①平面图中位置出格了，怎么办？

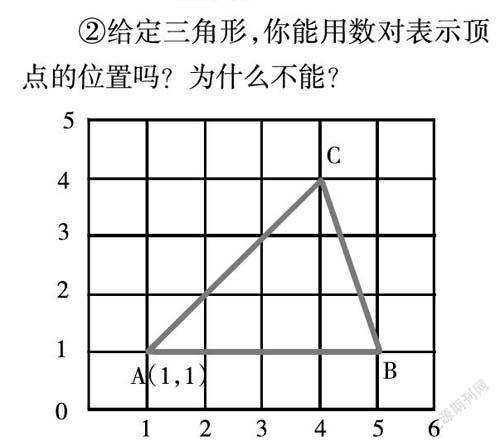
②给定三角形，你能用数对表示顶点的位置吗？为什么不能？

利用变式训练，一题多解或多题一解来开阔学生思路，引起思维变通，延伸思维。注重运用发散性思维方式提问，培养学生“立体思维”模式。徐利治教授曾指出：创造能力=知识量×发散思维能力。在这一训练中，学生的创造性思维得以培养。

三、总结深化，提升思维品质

学生的思维发展，应指在事物的不同层次上向纵、横两个方面发展，向问题的深度和广度发展，以达到对事物全面的认识的水平。为此，教师应重视在数学教学过程中，当前问题趋于解决后，由此及彼，系统地研究相关的问题，揭示数学问题的实质，构建数学思维模型，帮助学生提高思维的凝练能力。

张老师在小结提升环节引出：（1）确定一个点的位置，需要几个数？（2）真的都需要两个数吗？这两个问题将学生在确定位置时所要面临的一维线性空间、二维的平面空间、三维的立体空间、多维的无限空间进行巧妙的沟通、联系、梳理、铺垫。我们教育者要用发展的眼光确定教学目标的生长点与发展点，用心唱好“我从哪里来，要到哪里去”，懂得从孩子一生的经历来教学，开拓学生的思路，总结深化，促进学生思维品质的提升。

从张老师简明扼要的总结中，我们深深领会到：数学确实是一门应用性很强的学科，我们学习数学也是为了能够更好地解决生活中的问题。通过实践操作提升学生的思维品质，让学生能够看到数学的有趣、有用、真实的另一面。从而能够做到使用数学知识解决问题，帮助学生迅速提升数学思维品质。

学生的逻辑思维发展是一个长期的过程。因此，课堂教学应以学生思维的发展为核心，将思维训练贯穿于数学课堂教学的各个环节，抓住学生思维的起始点、转折点以及新的生长点、发展点，启发引导，努力培养学生思维的深刻性、灵活性、独创性；把时空有限的课堂变为“人人参与、个个思考”的无限空间，这样才能使绚丽的思维波澜飞溅起更高的思维浪花……