儿童立场下数学深度课堂的构建
孙敬彬
“儿童立场应是现代教育的根本立场”[1],这已得到越来越多教师的重视。但当儿童真正走到教育的中心位置,在课堂遇到“数学”后,经常发现许多课堂是有了“儿童”却没了“数学”,在热热闹闹中数学被浅表化了。因此,基于儿童立场,探寻用儿童自己的经验世界、认识水平以及思维方式等感悟数学本质的有效路径,构建用儿童的浅显数学经验触摸数学深刻内涵的“深度课堂”,显得尤为重要。
一、深度开发,化“隐”为“显”
儿童经验在数学学习中具有重要的作用。事实上,在与数学相遇之前,儿童就已经积淀了一些对数学的感性认识与经验,只不过这些经验多以零散的形式暗藏于其脑海深处。数学教材在编排时只是呈现了具体知识线索,在知识背后同样暗藏着许多数学思想方法。深度课堂要从儿童最本真的理解出发,学习最本质的数学,就需要深度开发儿童的内隐经验,以及知识背后暗藏的数学思想方法,通过变“隐”为“显”,让儿童自然走进数学,让数学更加贴近儿童。
如在“枚举策略”教学中,学习开始时的“热身活动”可以这样做。
师:把10根小棒分成两堆,可以怎样分?
(学生动手分小棒后相互交流自己的分法)
生:分成1和9、2和8、3和7、4和6、5和5。
结合学生回答板书:1 2 3 4 5
9 8 7 6 5
师:大家这样分有什么特点?为什么不继续分下去?
生1:这样分按照一定顺序,不会漏。
生2:再继续下去就重复了。
……
结合学生回答板书:有序 不重复 不遗漏。
可以看出,这次热身活动针对儿童内隐经验与暗藏的数学思想方法,把他们的一些浅表的、零散的、感性的认识逐步汇聚,同时也将枚举策略进一步具体化,有效促进了儿童对学习意义的认可,让儿童通过知识载体的学习不断发展经验,而当经验与思想充分“外显”之时,恰是两者交汇融合共生之机。
二、深度感悟,由“浅”入“深”
“思考是学生学习数学认知过程的本质特点,是数学知识的本质特征。”[2]学生对数学思考感悟的程度,影响其学习中数学化的进程。由于儿童的思考方式往往有明显的具象性,通常伴随着一些浅显、无序、不够全面、跳跃式思维状态,而数学思维具有极强的抽象性和逻辑性。因此,当儿童思考数学时,基于儿童立场就要充分考虑其思考方式,充分展现其思维过程;基于学科特点又要有效发展儿童的数学思维。而要实现两者的有效对接,让儿童思考与数学思维“淡妆浓抹总相宜”,就要引导儿童思考由“浅”入“深”,把思考逐步打上数学的烙印,以“浅”的内涵感悟,促进对数学“深”的理解。让儿童自发感受到思维方式完善提升的必要性,从而自觉促进其思维习惯养成,让儿童通过思考走向数学思维,并最终学会数学地思维。
如教学“认识分数”时,在分数的引入上,教师通过把一个苹果平均分成两份,促使儿童对“半个”的思考,然后通过用儿童喜欢的方式表示“半个”,呈现出方法上的丰富多彩,画苹果图,用半圆、用线段、用数字……最后及时对这些创造性表示方法进行对比沟通,“这些表示方法虽然有图有数各不相同,但它们之间也有相同的地方,你能找出它们之间相同之处吗?”再次引发学生深度感悟,他们很容易就会发现其共性的一面,即无论是哪种表示方法,其实质都是平均分成两份,而在这种感悟中也让学生清楚地看到了数与形在实质上的相同,意义上的相通,帮助学生更好地实现由整数到分数认知上的跨越。这样的认识过程由“浅”入“深”,让学生在对数学本质的感悟中实现“浅草才能没马蹄”。
三、深度活动,以“静”促“动”
儿童的天性是好玩、好动,他们喜欢通过用“动起来”的方式与数学对话,通过自己的观察比较、操作实验、讨论交流等去认识数学、理解数学。而数学的特性是抽象、理性,需要静下去从理性角度对活动中的认识与经验进行提升概括。因此,当儿童的天性与数学的特性在课堂上相遇,就需要既能“动”起来还能“静”下去的深度活动,把动手操作与静思内化结合起来,以“动”所“获”,为“静”成“思”,让“静”为“动”指明方向,增加活动的效度和深度,实现儿童天性尽情释放的同时,使他们的数学理性得以尽展光芒。
如教学“分数基本性质”时,可以先让学生通过折一折、涂一涂表示出正方形纸的1/2,接着让学生继续对折下去,找出几个与1/2相等的分数。这一环节让学生充分动起来,在折、涂、找的过程中帮助学生积累对分数间变化的原生认识与理解,而在下个环节安排学生对活动过程“静”下去反思,通过对“这些分数与1/2比起来什么变了,什么没变”的思考,把分子、分母间的变化规律逐步外显、提炼。可以看出,“动”帮助学生积累了许多活动经验,“静”则从意义角度理解“动”的变化实质,以“静”促“动”,让儿童实现了自己经验的逐步外化与提升,促成了对分数基本性质的初步概括。
四、深度体验,由“表”及“里”
数学作为理性之花,绽放的是“冰冷的美丽”,而儿童眼中的“美”是客观的、实实在在的。显然,“数学美”与儿童的审美很不统一。深度课堂需要对数学进行“审美化改造”,把“数学美”改造成儿童看得见、摸得着、能真切感受到的认知体验。然后让儿童以自己这些最真实的体会,缓慢地、反复地、持续地一次次触及数学的本质,不断掀开数学的面纱,感受数学形式美、内容美、价值美的本质内涵,以深度体验中的“真知灼见”生发对数学美的认同。而且借助深度体验帮助儿童感受到数学“火热”的温度、“迷人”的芳香,由表及里实现对“冰冷的美丽”的欣赏,让儿童以最真实深刻的体会勾勒数学的理性之美。
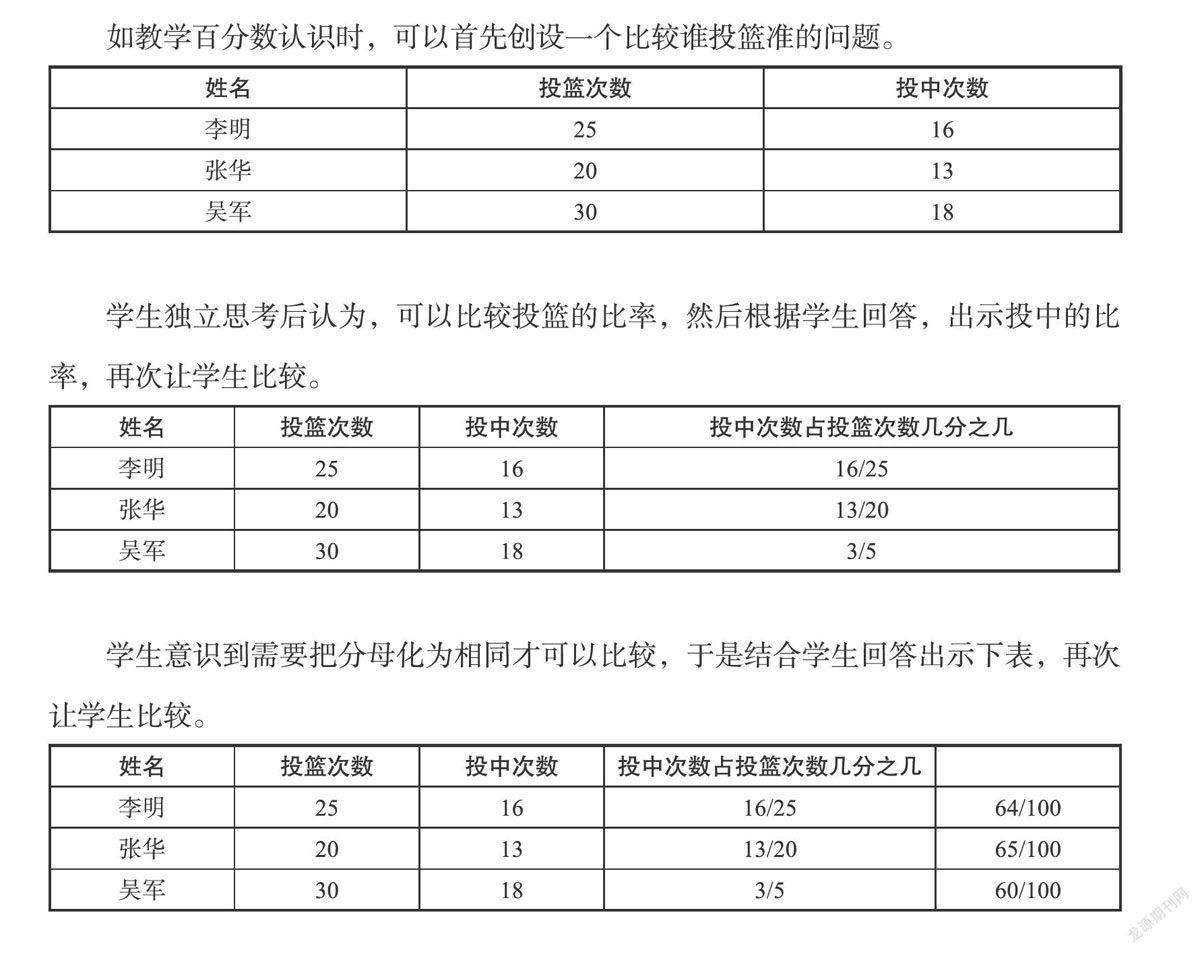
提问:现在能看出谁的投篮准吗?看前面投篮次数和投中次数两列能直接看出来吗?看第三列投中的比率能直接看出来吗?而根据百分数这列就能一眼看出,你觉得百分数有什么好处?
……
这样通过让学生反复比较、体验,从而真正让他们感受到百分数的应用价值,而随着体验的深入,数学之美也越发呈现,百分数的实质就会“水落石出”。
五、深度评价,由“此”及“彼”
“儿童作为学习的主体,对自己的学习最有评价权,对他人的学习最有建议权,而成人立场上的教师则最有发言权。”基于儿童立场,当儿童真正成为儿童时,他就有了“话语权”,评价便不再是教师的“独角戏”,于是,“生评”与“师评”此消彼长,成为需要相融的风景。深度课堂要发挥评价的正能量,让儿童的评价权有分量、建议权有质量,教师的发言权有含量,需要一种不分彼此的深度评价,在数学“在场”的情况下引导儿童学习的方向。
深度评价首先要关注儿童的数学现实如何变成数学实现。教师要从自己的角度及时给出客观建议,让儿童从评价中学会自我完善,同时要引导儿童对学习过程中遇到的问题、采用的方法、积累的经验自我审视,反思自己活动中哪些目标实现了,哪些还存在问题,以“师评+自评”实现对自己学习的主体回归。其次,要让学生在评价中学会评价,从事不关己、金口难开到学会分享自己的想法,引导学生向“帮助别人,从补充开始;评价别人,从欣赏开始”去转变,“你有什么看法或想法?”“有什么建议或补充?”“问题好在哪里?”“哪里做得好,哪里有问题?”等。通过互评让学生相互肯定,相互补充,把评价化为彼此成长的动力,让评价促成相互学习,共同发展,使课堂真正成为梦想开始的地方。
参考文献:
[1]成尚荣. 儿童立场,教育从这里出发[J]. 人民教育, 2007 (23)
[2]孔企平. 小学数学学习理论及其对课堂教学的启示[J]. 湖南教育(数学教师) , 2007 (6)
(作者单位:北京市海淀区中关村第三小学)
责任编辑:赵彩侠
zhaocx@zgjszz.cn

