大柔性飞行器的低阶建模方法及仿真分析

赵子绮，徐 亮，陆宇平

（南京航空航天大学 江苏 南京 211100）

大柔性飞行器的低阶建模方法及仿真分析

赵子绮，徐 亮，陆宇平

（南京航空航天大学 江苏 南京 211100）

大柔性飞行器模型采用有限元思路建模往往造成阶次较高，模型复杂等问题，不利于进行系统研究以及飞行控制一体化设计。文章基于常规刚柔解耦思路，建立了面向控制的大柔性飞行器低阶简化模型，用以对飞行控制进行研究，探索刚柔特性对飞行稳定性和控制设计的影响。通过仿真软件Matlab对建立的非线性大柔性飞行器模型运动特性进行分析。最终，得出了不同刚度条件下的仿真曲线，从而验证了模型正确性和可行性，为后续控制设计提供了实现基础。

大柔性飞行器；建模；仿真；模型配平

大柔性无人机（VFA）近年来成为特殊航空器研究热点，它能够在高空完成较大范围的长时间飞行［1］，然而质轻的特点使其在飞行中会产生明显的机翼结构变形，从而改变气动结构［2-3］。“太阳神”号无人机在极限飞行状态下的机翼上反角［4］可达到50°。然而，2003年6月的一次飞行试验中，太阳神无人机出现震荡导致飞机解体坠毁。在其后NASA发布的事故调查中发现，飞机在遭遇强湍流时，引起了翼段向上弯曲，致使整个机翼发生严重俯仰震荡，超出了飞机结构的扭转极限，报告同时还进一步强调后续将展开对大变形无人机的非线性的几何结构建模研究［5］。

当前开展的完成度和精确性较高的几何非线性结构模型主要有Hodges-Dowell理论梁模型和基于Total Lagrange （TL法）、Updated Lagrange（UL法）的有限元模型。其中，密歇根大学Hodges-Dowell等人在NASA的资助下，对非线性梁模型的高空长航时飞机进行了非线性的气动弹性配平及稳定性计算代码（NATASHA）［6-8］。TL法和UL法是几何非线性问题中较为常见和重要的两种算法。TL法以结构的初始位形，单元的局部坐标系不随单元的变形前的初始坐标系。UL法的第n+1级加载时以第n级加载终了时的位形为参照位形，即参照位形是单元变形后的位形［9-10］。

以上3种方法都是基于有限元思想建立的非线性几何模型，其在保证精确度的基础上，会导致模型阶次过高，例如美国国防部高级研究计划局（DARPA）在研的“秃鹰”模型［11］，其线性化的状态空间模型达到707阶，这类高阶模型通常不利于用作系统研究。Gibson等人［12］面向控制算法提出了一种刚柔分离的简化建模思路，将飞机机翼结构简化为翼板和弹性铰链的组合，从而获得一个利于控制器设计较为低阶的数学模型。文中以此方法为基础，建立了5段机翼的完整大柔性飞行器机翼非线性模型。

1　结构建模

文中以“秃鹰”飞行器的飞翼式模型结构布局进行模型搭建，其外形结构如图1所示。该飞行器主体由5个外形相同的机翼连接而成，在各翼板前端装配叶片式发动机提供飞机所需油门推力，只有处于中间位置的3号机翼所连尾翼附带方向舵，其余机翼均为平尾，实物如图2所示［13］，机翼弹性变形集中在铰链位置j，η表示翼板间的二面角，如图3所示。

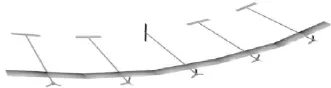
图1　飞翼式布局大柔性飞行器外形结构

图2　大柔性飞行器小型实物模型

图3　大柔性飞行器结构及坐标系示意图

1.1翼板角动量

令飞行器整体角速度为

这里，下标f表示机体重心位置，上标｛g｝表示机体坐标系，机体坐标系下的整体线速度可定义为

根据飞行器的整体结构可知，由于变形只涉及铰链位置的弯曲变形，利用向量和坐标系转换关系，可得各翼板和铰链j1，j2，j3，j4处速度。

由速度和角速度通过式可以求得各机翼角动量相对于铰链处的大小

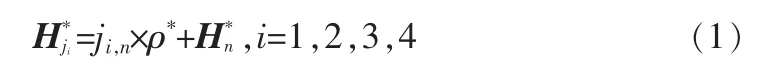
其中，加号前部分为平移转动原点导致的附加量，加号后H*n为翼板自身角动量，H*ji为i号机翼在对应铰链位置处的角动量（向内取铰链点），ρ*为其线动量，假定各机翼均为左右对称结构，所以转动惯量张量矩阵非对角线上的元素皆为0。

对角线元素为机翼相对于各坐标系的转动惯量，由角动量定义H=I×ω，可得各翼板在对应铰链处（取内侧）的角动量

1.2铰链处动力学方程和铰链力矩

根据结构动力学方程，只考虑机翼弯曲变形，将弯矩定义为有关机翼二面角的量，可令

此处，Mj为机翼铰链处产生的力矩，kc和kk分别铰链阻尼和铰链刚度，中文关心的是弯曲变形带来的铰链扭转力矩对飞行性能的影响，因此将其视为机翼x方向角动量的微分。

Mj的推导主要在各机翼的局部机体轴系下进行：取机翼坐标系下z轴方向的气动力与机翼沿z轴的分量同重心到气动焦点的叉乘值作为作用在铰链位置的铰链力矩：

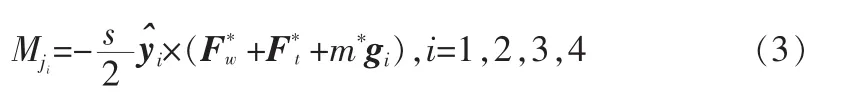
其中，m*为单段翼板质量，F*w和F*t分别为机翼和尾翼在各机翼准坐标系下受力情况。由于飞行姿态和飞行器的变形，重力加速度与二面角大小有关，需要进行适当的坐标系转换。

2　气动建模

本节主要对大柔性飞行器进行气动建模，通过飞行器展向弯曲变形的几何结构关系推导各翼板气动力和气动力矩的关系。气动力的计算采用已知飞行器整体迎角和侧滑角，通过结构关系得出各翼板自身的气流角，通过气流角得到局部准坐标系下的气动力，最后通过坐标变换到机体气流系下。这里直接给出迎角和侧滑角关系式（左加右减）。

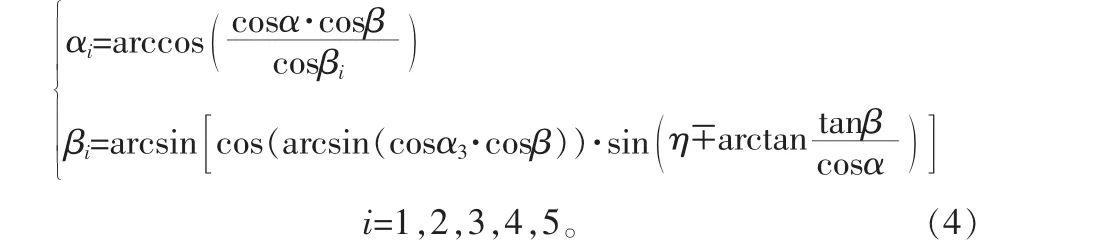
2.1气动力公式推导

作用在飞行器上的外力共3种，重力、气动力和推力。气动力对每段翼板单独分析，以机翼各自气流角为对象。

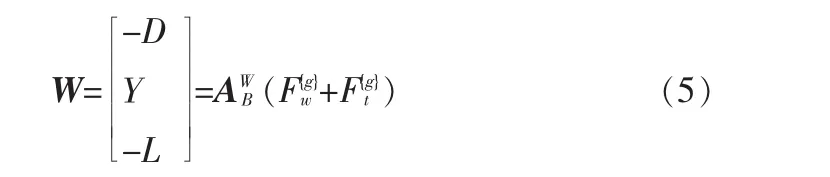
其中AWB为机体系到气流系转换矩阵，F｛g｝w和F｛g｝t分别为机翼和尾翼在机体系下受到气动力载荷。此处已将各翼板的气动力转换到整体机体轴中。利用飞行力学［14］和模型自身特点可以得到单段机翼升阻力公式：

式中，L、D为升力和阻力，下标w、t区分机翼和尾翼，Q为当地动压，S为机翼或尾翼参考面积，δa为副翼偏转角，δe为升降舵偏转角，CL、CD分别为飞行器升力系数和阻力系数。

侧力主要体现在侧滑时垂尾和具有上反角的边翼的气动力上，当机翼发生侧滑时，侧滑角的部分分量会影响到边翼的迎角带来一定的迎角增量，且左右侧呈叠加状态，从而导致侧力的产生。将各机翼气动力通过坐标系转换至整体机体系下，分别得到机翼和尾翼的升力，阻力和侧力：

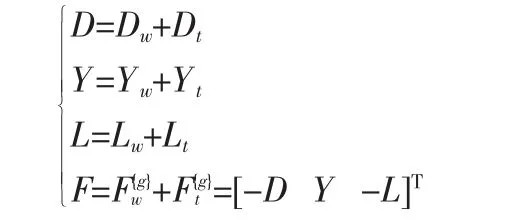
2.2气动力矩公式推导

每段翼板的气动力相对于质心会产生气动力矩，决定了飞行器的俯仰、滚转和偏航运动，在切线坐标系下，通过求解各翼板气动力对质心的力矩作用，再结合飞行器副翼的气动力矩，可求得飞行器总的气动力矩：

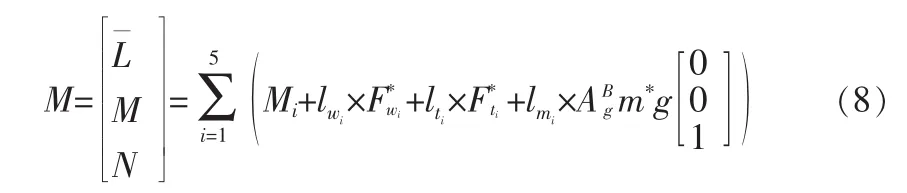
其中，ABg为地轴系到体轴系的转换矩阵，Mi=［L¯′iM′iN′i］T是角速度、操纵舵面和上反角引起的动态滚转、俯仰、偏航力矩［14］

上式中，CL¯i，CMi，CNi是各方向力矩系数，cw是机翼弦长，¯p为机翼滚转角速度，δa，i、δe、δr为分别为副翼、升降舵、方向舵的舵面偏转角，相应地，CLδa、CMδ、CNδr为滚转、俯仰、航向操纵导数，式中，由于机翼两侧方向不同，导致上反角的变化率对机翼的滚转力矩的影响不一，这里左侧取正，右侧取负。

2.3状态量的选取

选取17个状态作为研究对象，分别为速度，气流角α、β，姿态角 φ、θ、ψ，角速度 p、q、r，二面角 η1、η2、η3、η4及其导数η.1、η.2、η.3、η.4。输入量为发动机推力T，以及舵面偏转角δe、δr、δa1、δa2，需要说明的是本文采用的是常规横纵向解耦，依据常规的飞行器分析方法优先对纵向进行研究。另外，将利用水平无侧滑飞行条件可解耦得到气流角公式［14］

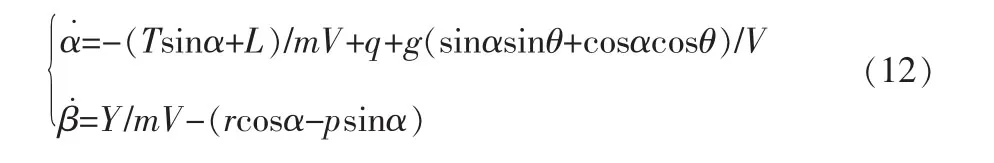
由机体坐标轴系与地面坐标轴系之间的关系，不难写出姿态角速度（θ.，φ.，ψ.）与机体坐标轴系的3个角速度分量（p，q，r）之间的关系

机体轴下的角速度的变化主要由气动力矩和惯量张量的变化导致，

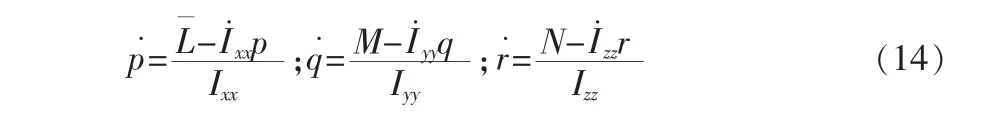
铰链处动力学方程变形得到式关于二面角的二次导方程：

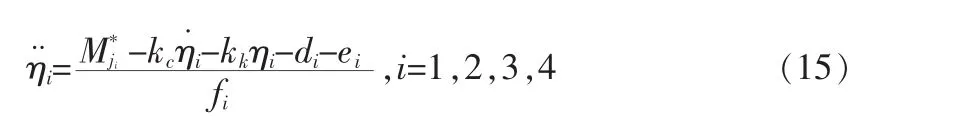
其中di，ei，fi为上文推倒结果，公式过长此处略去，读者可自行推倒。

3　仿真验证

将模型导入Matlab的S函数，代入通过文献［12］得到的Helios飞行器的几何结构参数和气动参数，在给定不同刚度值条件下，利用Matlab中trim（）函数［15］，得到表1的配平数据。

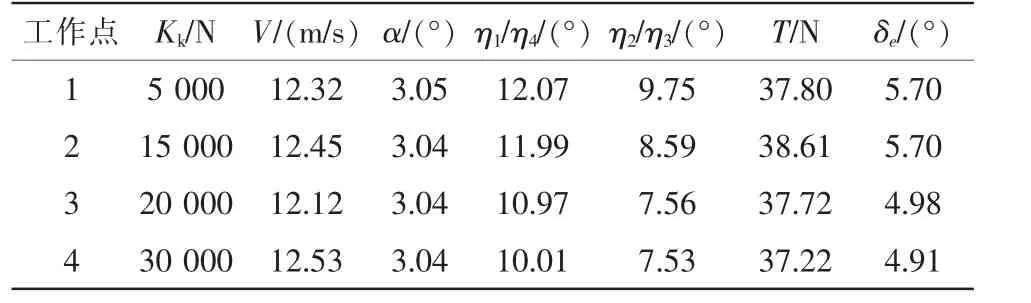
表1　大柔性飞行器配平平衡点

将表1配平点数据带入模型，在不同柔性单元刚度值下，得到如图4的飞行性能仿真曲线，仿真时间为100 s。

由图可知，非线性模型在平衡点附近做微幅震荡收敛，最终稳定在平衡点上。当刚度随着工作点1到4逐渐增加时，速度振荡幅度减小，变化趋势一致，迎角和俯仰角的振荡幅度亦随刚度增大而减小，猜测迎角维持长周期振荡的原因可能与翼二面角有关。而俯仰角速度在前期剧烈振荡后基本趋于稳定。图（d）和（e）为飞行器左侧的翼二面角变化情况，由于柔性单元刚度的增加二面角振荡幅度显著减小，而由于阻尼不变，翼二面角振荡周期基本一致。

4　结束语

文中介绍了一种面向控制设计的低阶大柔性飞行器建模方法，利用集中柔性单元的做法，将模型刚柔解耦，结合常规飞行力学进行受力分析，得到了完整大柔性飞行器低阶非线性模型。最后通过仿真软件对模型进行了准确性进行了验证，实验证明了该模型可作为大柔性飞行器的有效近似模型。

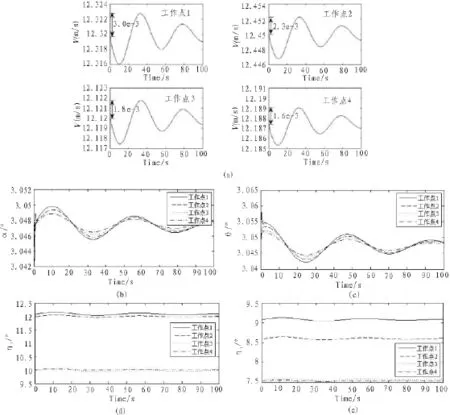
图4　变刚度条件下的飞行性能响应曲线

［1］Shearer C M，Cesnik C E S.Nonlinear flight dynamics of very flexible aircraft［J］.Journal of Aircraft，2007，5（44）:1528-1545.

［2］潘登，吴志刚，杨超，等.大柔性飞机非线性飞行载荷分析及优化［J］.航空学报，2010，31（11）:2146-2151.

［3］Whitson S.The Proteus，Giving Shape to Form Unknown［J］. Private Pilot，1988-12，33（12）:44-50.

［4］Kirk Flittie，Bob Curtin.Pathfinder solar-powered aircraft flight performance［R］.1998.

［5］Youngblood J W，Talay T A.Solar-powered airplane design for long-endurance，high-altitude flight［R］.1982.

［6］Patil M J，Hodges D H，Cesnik C E S.Nonlinear Aeroelasticity and Flight Dynamics of High-Altitude Long-Endurance Aircraft［R］.1999.

［7］Patil M J，Hodges D H.Flight Dynamics of Highly Flexible Flying Wings［R］.Journal of Aircraft，2006，43（6）:1790-1798.

［8］Jaworski J W.Nonlinear Aeraelastic Analysis of Flexible HighAspectRatioWingIncludingCorrectionwith Experiment［D］.Duke University，2009.

［9］Zhang Jian，Xiang Jinwu.NonliearAeroelastic Response of High-Aspect-Ratio Flexible Wings［J］.Chinese Journal of Aeronautics.2009，22（4）:355-363.

［10］朱慈勉，吴维华，陈栋.TL法和UL法对刚架弹性大位移分析的适用性［J］.力学季刊，2001，22（1）:104-111.

［11］GadientR，WiseK，LavretskyE.Very flexible aircraft control challenge problem［C］//Guidance，Navigation，and Control and Co-located Conferences，Minneapolis，Minnesota，AIAA，2012，（4793）:1-6.

［12］Travis E.Gibson，Anuradha M.Annaswamy.Modeling for Control of Very Flexible Aircraft［C］//Guidance，Navigation，and Control Conference，Portland，Oregon，AIAA，2011-6202.

［13］Christopher M.Shearer.Coupled nonlinear flight dynamics，aero-elasticity，and control of very flexible aircraft［D］.Michigan: University of Michigan，2006.

［14］吴森堂，费玉华.飞行控制系统［M］.北京：北京航空航天大学出版社，2005.

［15］薛定宇.控制系统计算机辅助设计:MATLAB语言与应用［M］.北京：清华大学出版社有限公司，2006.

A low order modeling approach and simulation for very flexible aircraft

ZHAO Zi-qi，XU Liang，LU Yu-ping
（Nanjing University of Aeronautics and Astronautics，Nanjing 211100，China）

The VFA model was usually produced by finite element，which lead to the problem of high order and complexity，it was harmful for doing research on the system and brought difficulty to integrated design for flight control.In this paper，a new modeling method was proposed for flight control，using conventional decoupling for rigid coupling，which could be used to research the flight stability caused by rigid characteristics.Then，the simulation software（Matlab）was applied to analysis the kinematics of the non-linear VFA model，whichcorrectness and feasibility was verified，and in order to realize the control design further，the simulation to analyze the flight performance was also done in the condition of different value of stiffness.

very flexible aircraft；modeling；simulation；model trimming

TN96

A

1674－6236（2016）16-0005-04

2016-02-24稿件编号：201602124

国家自然科学基金（11572149）；中央高校基本科研业务费专项资金资助：南京航空航天大学研究生创新基地（实验室）开放基金（kfjj20150322）

赵子绮（1991—），男，安徽蚌埠人，硕士。研究方向：先进飞行控制。