混凝土重力坝接触爆炸的响应及破坏特性分析*
徐 强,曹 阳, 陈健云,李 静,刘 静
(大连理工大学 建设工程学部, 辽宁 大连 116024)
混凝土重力坝接触爆炸的响应及破坏特性分析*
徐强,曹阳, 陈健云†,李静,刘静
(大连理工大学 建设工程学部, 辽宁 大连116024)
运用显式非线性动力分析程序LS-DYNA模拟正常蓄水位及空库条件下混凝土重力坝接触爆炸.考虑爆炸荷载作用下混凝土的高应变率的影响,采用HJC(Holmquist-Johnson-Cook)本构模型模拟坝体混凝土的损伤破坏及塑性变形的破坏特性.首先构建炸药-空气-水-混凝土试块模型并对其进行了模型验证.然后构建炸药-空气-库水-坝体-地基之间的动态全耦合模型,并对正常蓄水位与空库条件下TNT炸药接触爆炸的大坝动态响应及破坏特征进行了分析.研究结果表明:运用该方法研究混凝土重力坝水下接触爆炸引起的结构动力响应问题,具有稳定的可靠性,弥补了试验研究的不足.正常蓄水位下,在上游布置炸点对坝体的动力响应及损伤程度影响更大,因此在研究大坝抗爆性能时,应重点关注正常蓄水位条件下大坝上游侧炸点水下接触爆炸时大坝的破坏特性.
混凝土重力坝;HJC本构模型;水下接触爆炸;响应;破坏特性
改革开放以来,国内建设了很多高坝,如已建的三峡大坝、溪洛渡拱坝等.大坝作为水工建筑物的一部分,其安全性是国家安全防护的重中之重.随着现代战争技术与武器的发展,大坝已经成为战争中重要的打击与争夺对象,特别是近年来恐怖袭击频繁,防止大坝结构冲击和研究大坝的抗爆性能至关重要[1-2],因此对爆炸荷载作用下的水工大坝破坏特征开展研究具有重大的现实意义.
20世纪末期,随着计算机的发展,对爆炸荷载作用下大坝的数值计算研究迅猛发展.目前,国内对于大坝爆炸荷载作用的研究主要是将理论、实验和数值模拟相结合[3],并且主要集中在重力坝、拱坝和土石坝方面.在重力坝的研究中,张社荣等采用SPH-FEM耦合算法分析了混凝土重力坝水下爆炸的损伤,用SPH法[4]模拟爆炸点附近的坝体变形破坏,用FEM法模拟爆炸点远处的变形破坏并对水下接触爆炸与非接触爆炸的损伤严重性进行了对比[5],建立了全耦合模型分析水下爆炸冲击荷载下重力坝的破坏特点[6];李本平[7]通过模拟炸弹连续打击混凝土重力坝,研究大坝的破坏效应;Yu[8],徐俊祥和刘西拉[9]对混凝土重力坝水下爆炸建立了全耦合模型,以坝体、坝基、炸药、水、空气为计算域模拟了混凝土重力坝的水下爆炸动力响应. 对于拱坝,张社荣和王高辉运用数值全耦合模型,考虑混凝土高应变率效应,采用三维有限元法分析了水下不同位置爆炸冲击荷载下高拱坝的破坏模式[10],并针对重力拱坝的结构特点分析了大坝在水下爆炸荷载作用下的破坏机理[11].考虑土石坝的爆炸破坏,刘军等[12]运用显式非线性动力分析程序LS-DYNA对爆炸荷载作用下的大型土石坝进行了数值模拟计算,土石坝在爆炸荷载作用下,在爆炸接触部分发生局部破坏;宋娟等[13]运用共节点算法、接触算法和任意拉格朗日-欧拉(ALE)算法模拟了土坝中的爆炸,并且考虑了黏性边界、三维一致黏弹性边界和远置边界,分别模拟计算了3种算法及3种边界下的破坏特性,并对结果进行了比较分析.童桦、罗松南等[14-15]对应力波在混凝土中的传播进行了研究.
随着碾压混凝土技术的发展,国内已建成许多混凝土重力坝,其安全也是水利工程的核心问题.大坝遭到爆炸袭击,必然造成巨大的灾难,对于混凝土重力坝工程结构的防护和对其抗爆性能的研究逐渐引起关注.重力坝爆炸荷载作用下的破坏按空间位置分为水下爆炸、库区近空爆炸、坝体爆炸.研究表明,水下爆炸比其他爆炸形式具有更大的破坏性,水下爆炸根据炸心距的不同也会对大坝产生不同的损伤破坏.对于水下爆炸的研究已有很长的历史.1948年Cole R H出版的《水下爆炸》[16]分析了水下爆炸的机理,并推导了水下爆炸冲击波超压计算公式,得到广泛的理论与实践运用.近代,随着计算机计算能力的提高,水下爆炸研究在数值模拟方面得到了迅速发展,已经成为重要研究方法之一.
本文运用显式非线性动力分析程序LS-DYNA模拟混凝土重力坝水下爆炸.考虑爆炸作用荷载下混凝土的高应变率[17],通过在上下游不同位置设置炸点,分析上游水库正常蓄水位和空库爆炸时混凝土重力坝的损伤破坏、结构动力响应及其抗爆性能,为混凝土重力坝的抗爆安全评估和抗爆防护设计提供理论参考.
1 坝体混凝土及坝基岩体本构模型
1.1坝体混凝土本构模型
HJC本构模型是一种率相关混凝土本构模型,综合考虑了混凝土材料的大应变、高应变率及高压效应.HJC本构模型用等效强度取代静态屈服强度,如图1(a)所示,HJC屈服方程如式(1)所示.
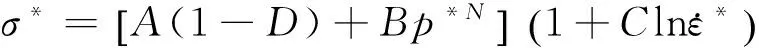
(1)
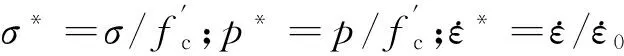
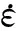
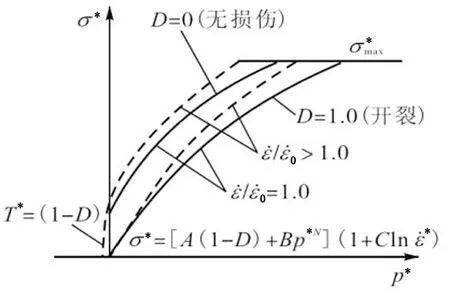
(a)等效强度模型

(b)混凝土损伤模型
(c)静水压力与体积应变曲线图1 HJC混凝土本构模型Fig.1 HJC constitutional law models of concrete
材料的损伤累积用损伤度D来表示.材料的损伤累积主要来自于等效塑性应变、塑性体积应变和静水压力的影响,如图1(b)所示, HJC损伤演化方程如式(2)所示.
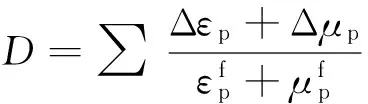
(2)

混凝土损伤常数EF,min是混凝土破坏时允许的最小塑性应变,满足式(3).
D1(p*+ T*)D2≥EF,min.
(3)

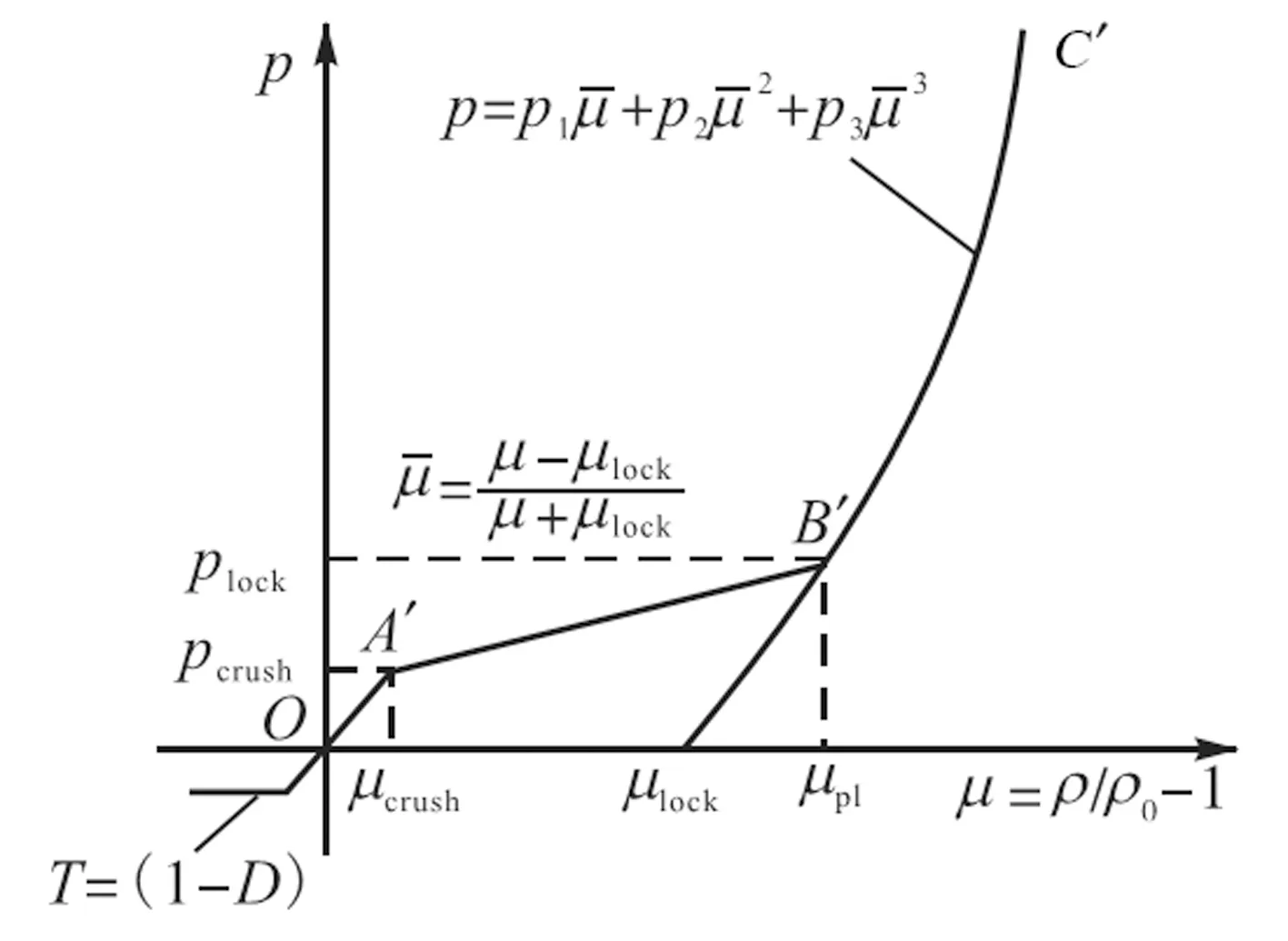
HJC本构模型采用状态方程描述静水压力与体积应变之间的关系.混凝土的状态方程可以分为3个阶段.线弹性阶段在第一个过程(OA′)中,静水压力和体积线应变满足线性关系K=p/μ;过渡阶段在第二个过程(A′B′)中,混凝土材料内的空洞逐渐被压缩,以致产生塑性体积变形;完全密实阶段在第三个过程(B′C′)中,当压力达到plock值时,混凝土内部气孔被完全压碎,其关系常用三次多项式(4)表示.
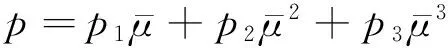
(4)
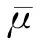
1.2坝基岩体本构模型
坝基岩体本构模型采用塑性硬化模型.该模型属于各向同性、随动硬化或各向同性和随动硬化的混合模型,与应变率相关,考虑失效,如式(5)所示.
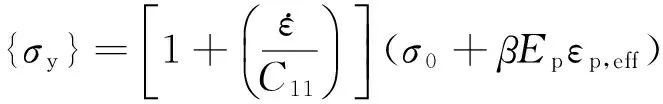
(5)
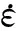
1.3材料模型参数及状态方程
炸药采用MAT_HIGH_EXPLOSIVE_BURN高能炸药材料模型描述,其JWL状态方程如式(6)所示.
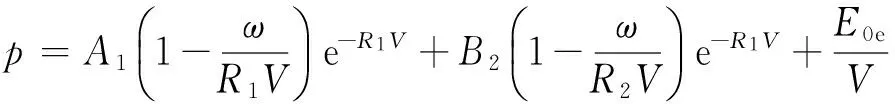
(6)
式中:A1,B2,R1,R2,ω为材料参数;p为压力;V为相对体积;E0e为初始比内能.
水采用可压缩无旋流体,水的状态方程为EOS_GRUNEISEN,其状态方程如式(7)所示.
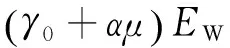
(7)
式中:C22,α,S1,S2,S3,γ0均为水的材料参数;EW为水的初始单位质量内能;μ=ρ/ρ0-1,ρ0为参考密度,ρ为水的密度.
空气采用EOS_LINEAR_POLYNOMIAL状态方程描述,空气简化为无黏性理想气体,其状态方程如式(8)所示.
p=C0+C1μ+C2μ2+C3μ3+
(C4+C5+C6μ2)Ea.
(8)
式中:C0,C1,C2,C3,C4,C5,C6均为材料参数;Ea为初始单位质量内能.
2 模型验证
为了验证运用显式非线性动力分析程序LS-DYNA模拟混凝土重力坝水下爆炸的可行性,用LS-DYNA建立重力场下的水下爆炸模型.通过此模型和文献[17]中提及的长江科学院刘美山等进行的混凝土深水爆炸实验进行对比.炸药采用岩石乳化炸药,炸药的JWL状态方程及材料相关参数见表1,水的状态方程及材料相关参数见表2,空气的状态方程及材料相关参数见表3.混凝土立方体试件材料的本构模型采用HJC本构模型描述,其材料参数见表4.此模型采用实验中的实际尺寸模拟在重力场下的混凝土水下爆炸损伤过程,有限元1/4模型及尺寸如图2所示.混凝土试件边长为100 cm,装药半径为1.6 cm,装药筒半径为5 cm,炸药周围的装药筒空隙用水填充,炸药的装药量为50 g,混凝土周围加水压,模拟水深为25 m.水外表面采用无反射边界.
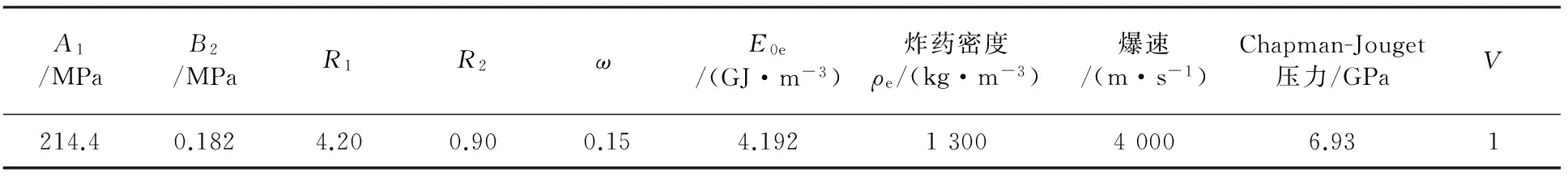
表1 岩石乳化炸药状态方程及材料相关参数

表2 水的状态方程及材料相关参数

表3 空气的状态方程及材料相关参数

表4 混凝土HJC本构模型材料参数
图3给出了分析过程中的能量平衡图.由图3知,爆炸刚开始时动能迅速增加,随后下降趋于稳定,同时内能快速下降达到稳定,总能量减少趋于稳定(本例作为一个开放系统),满足能量守恒定律.图4给出了50 g装药25 m水深的水下爆炸实验结果和50 g装药25 m水深的数值实验结果.如图4所示,实验结果中水下爆炸后混凝土试件外表面产生了十字形的裂纹,没有裂开;数值实验模拟结果表明混凝土试件外表面出现了十字形的损伤破坏.综上所述,实验结果和数值模拟结果接近并且爆炸过程中能量平衡,从而说明了运用显式非线性动力分析程序LS-DYNA模拟混凝土重力坝水下爆炸的稳定可靠性.
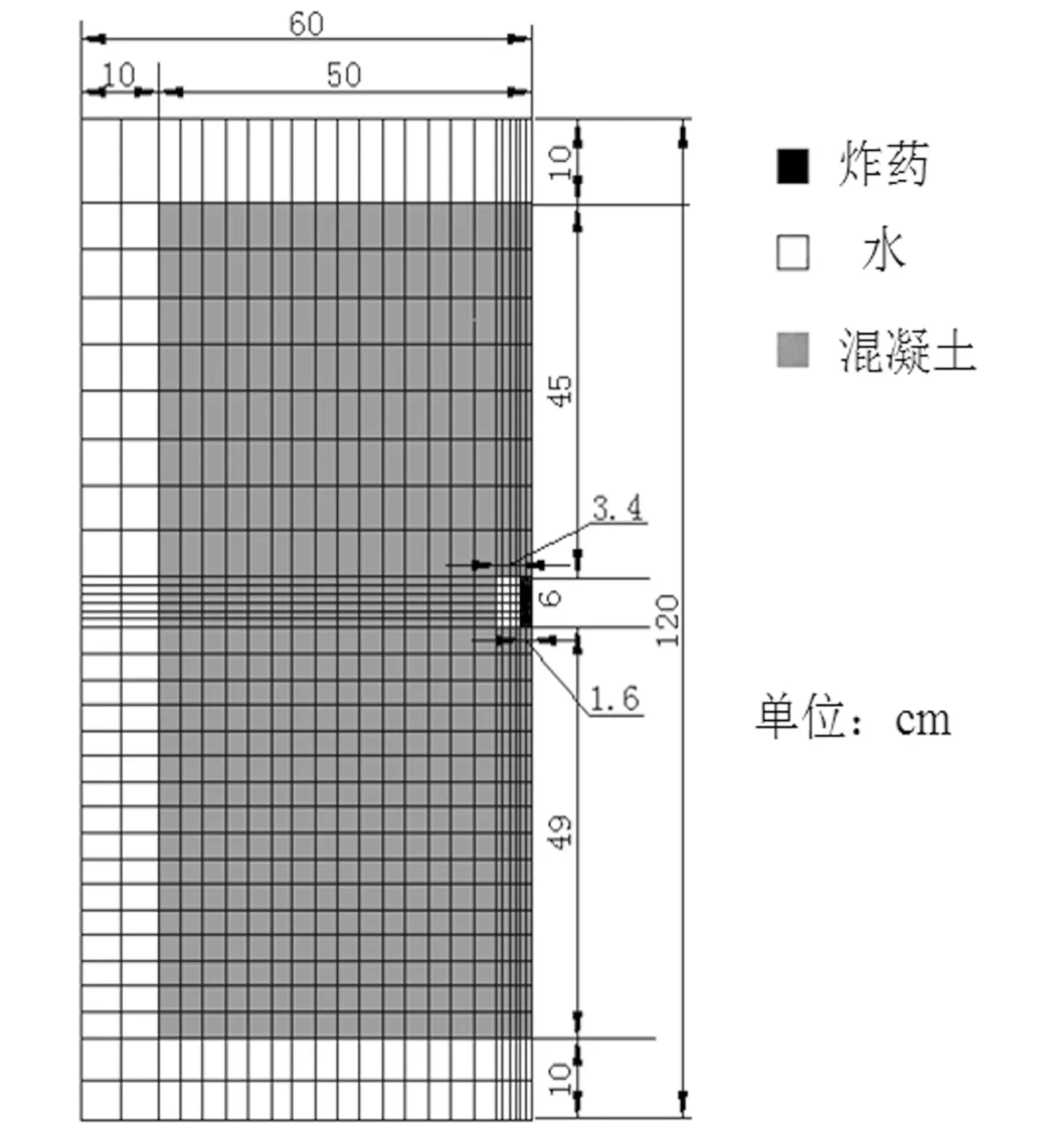
图2 用于验证的计算模型Fig.2 The model for verification
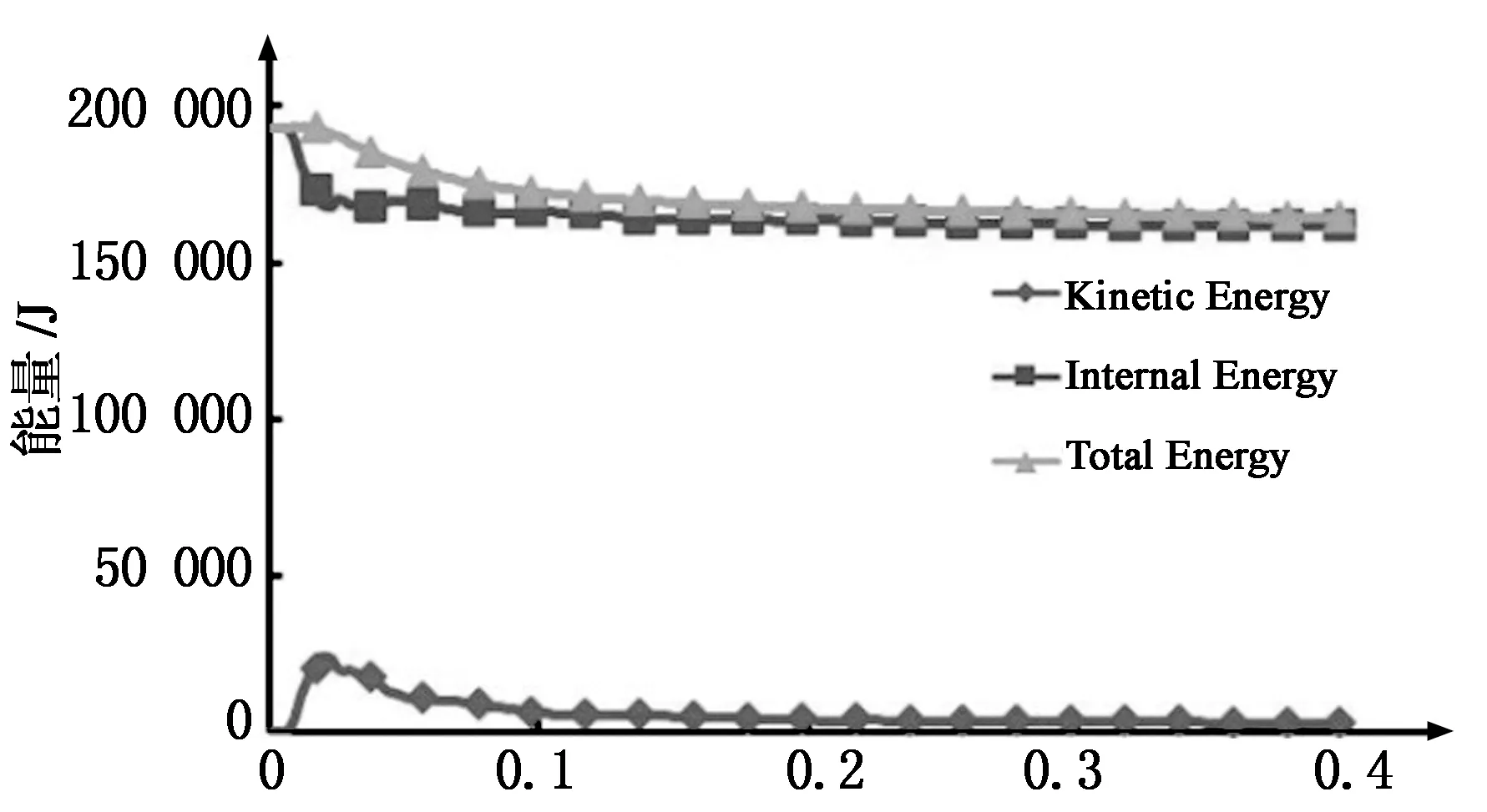
时间/ms图3 能量平衡图Fig.3 Energy balance curves

图4 实验结果和数值模拟的破坏模式Fig.4 Failure mode of experimental results and numerical simulation
3 接触爆炸下混凝土重力坝的抗爆性能分析
3.1计算模型
本文研究对象为混凝土重力坝非溢流坝段,取印度Koyna大坝作为计算模型,水库正常蓄水位为93.5 m,坝高103 m,计算区域如图5所示.正常蓄水位模型由空气、TNT炸药、库水、大坝和地基组成;空库模型由空气、TNT炸药、大坝和地基组成;采用Lagrange网格建模,网格单元高度为0.5 m;在大坝的上游和下游分别布置5个炸点(上游炸点编号为1~5,下游炸点编号为6~10,其中编号1~2与6~7之间的间隔为12.5 m,其余间隔为18 m).本文中TNT炸药的用量为14.88 t,炸药的炸点位置布置图如图5所示,TNT炸药的JWL状态方程及材料相关参数见表5;水的状态方程及材料相关参数见表2;空气的状态方程及材料相关参数见表3.混凝土重力坝坝体材料的本构模型采用HJC本构模型描述,其材料参数见表4.地基采用塑性硬化模型,其材料参数见表6.边界条件采用如下形式,库水、上下游空气采用无反射边界,使得人工边界上无应力波反射,来模拟无限的库水和空气.地基、坝体横河向方向施加法向约束,地基底部施加全约束.

表5 TNT炸药的状态方程及材料相关参数

表6 塑性硬化模型材料参数
3.2正常蓄水位与空库条件下接触爆炸时混凝土重力坝的抗爆性能分析
3.2.1正常蓄水位与空库条件下同一炸点不同测点(A,B测点)的时程分析
为了比较分析正常蓄水位与空库条件下接触爆炸时坝体的动力响应,分别在坝顶、下游折坡处取A,B测点.由于计算工况较多,且在正常蓄水位与空库条件下加速度、速度和位移时程曲线相似,仅以炸点1(炸药安放在炸点1处)为例,炸点1及A和B测点位置如图5所示.
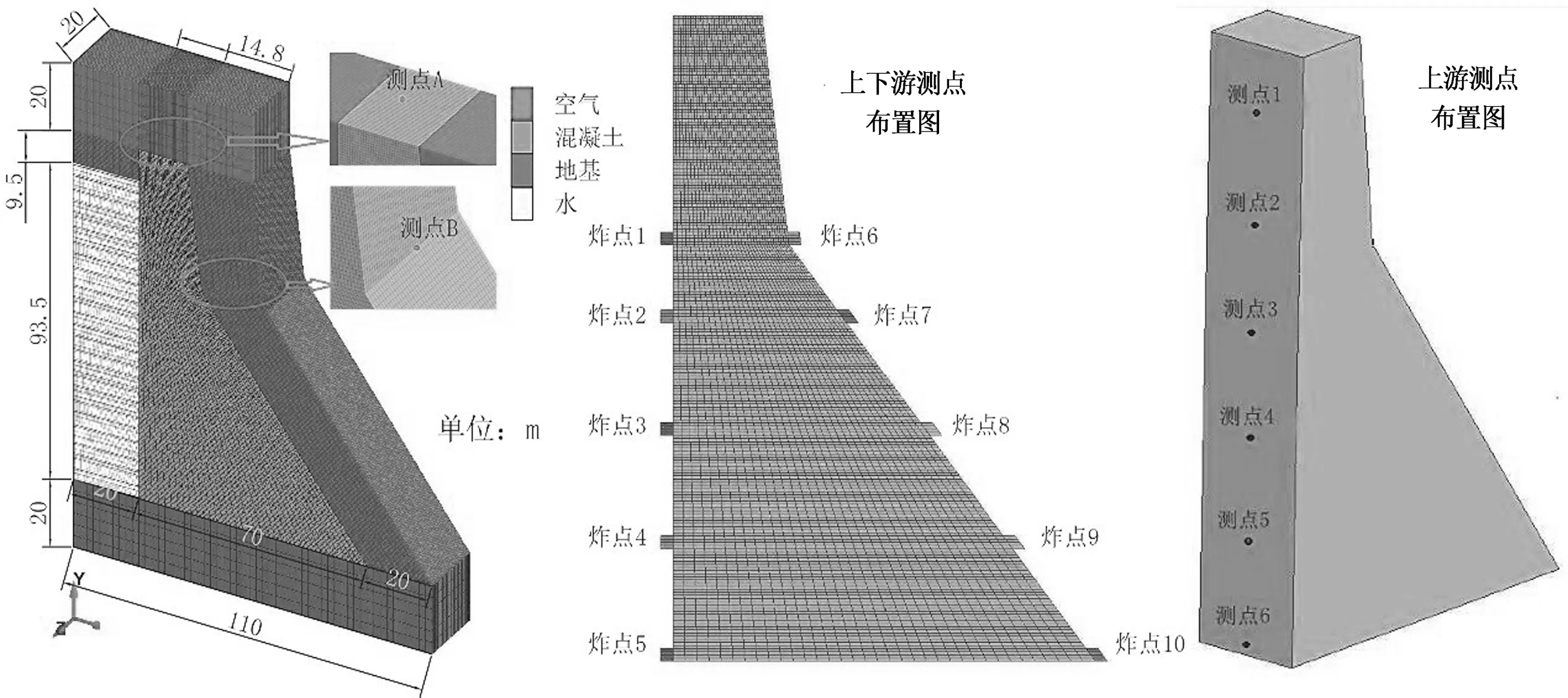
图5 重力坝接触爆炸的计算模型Fig.5 The model for simulating the concrete gravity dam subjected to contact explosion
图6(a)给出了顺河向接触爆炸A与B两测点的加速度时程曲线.通过分析两测点的加速度可知,A测点正常蓄水位时的最大峰值加速度小于空库时的最大峰值加速度约16%,B测点正常蓄水位时的最大峰值加速度大于空库时的最大峰值加速度约68%;由于动水压力的影响,正常蓄水位比空库的峰值加速度略微滞后,且持续时间较空库长,波动幅度也较大.综上所述,大坝在正常蓄水位时接触爆炸荷载作用下的总体加速度响应较在空库荷载作用下剧烈,尤其在下游折坡处更为明显.
图6(b)给出了顺河向接触爆炸A与B两测点的速度时程曲线.通过分析两测点的速度可知,A测点正常蓄水位时的最大速度约为空库时最大速度的2.23倍,B测点正常蓄水位时的最大速度约为空库时最大速度的2.75倍;由于动水压力的影响,正常蓄水位比空库的速度时程略微滞后,且持续时间较空库长,波动幅度也较大,从而对大坝的破坏也较大.综上所述,大坝在正常蓄水位时接触爆炸荷载作用下的速度响应比在空库荷载作用下剧烈得多.
图6(c)给出了顺河向接触爆炸A与B两测点的位移时程曲线.由A与B测点可知,接触爆炸时,正常蓄水位的峰值位移均比空库时的峰值位移大,并且由于动水压力的影响,正常蓄水位的位移波动较空库时的大,从而对大坝的破坏也较大.
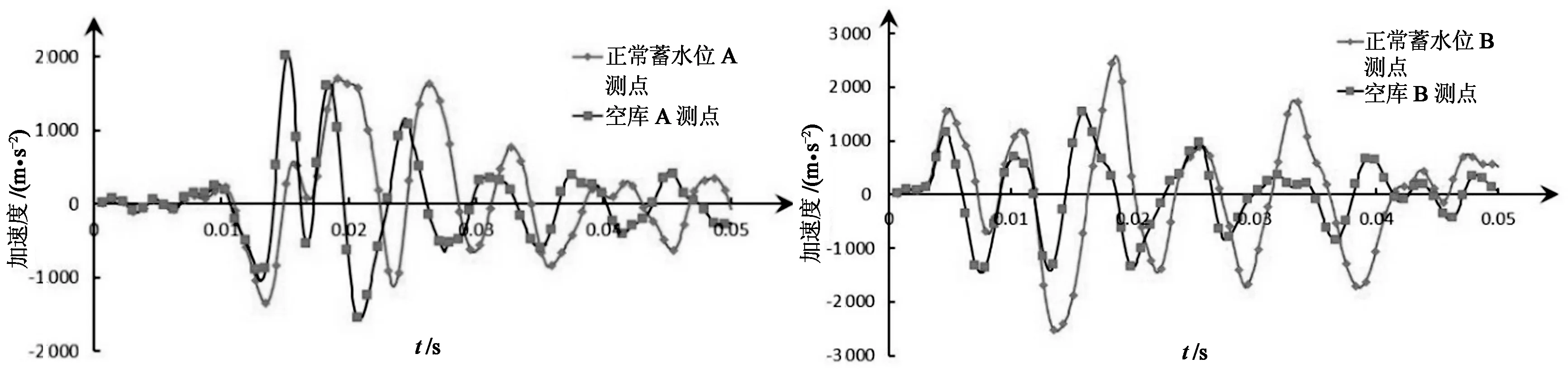
(a) 测点A,B顺河向加速度对比
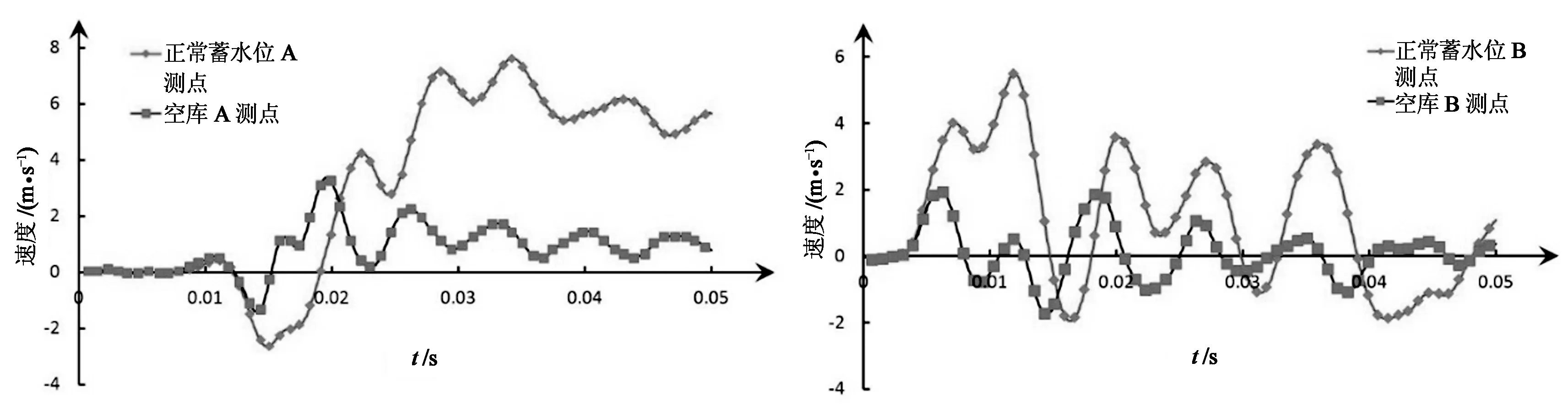
(b) 测点A,B顺河向速度对比

(c) 测点A,B顺河向位移对比图6 测点A,B顺河向时程对比Fig.6 Contrastive analysis of time-histories along the river at points A,B
3.2.2正常蓄水位与空库条件下不同炸点不同测点的动力响应分析
图7给出了接触爆炸荷载作用下正常蓄水位、空库条件下不同炸点不同测点处的动力响应(炸点位置及测点位置如图5所示,测点6的高程为2 m,每20 m增加1个测点,共设6个测点).由图7可知,在爆炸荷载作用下,总体上正常蓄水位的顺河向加速度、速度、位移响应幅值比空库更加剧烈.对于此大坝,由动力响应曲线得出,在炸点2处爆炸,产生的动力响应在高程62 m处(折坡高程附近)最为剧烈,并且在炸点附近的加速度、速度及位移响应幅值基本呈三角形分布.
3.2.3正常蓄水位与空库条件下不同炸点的毁伤特性分析
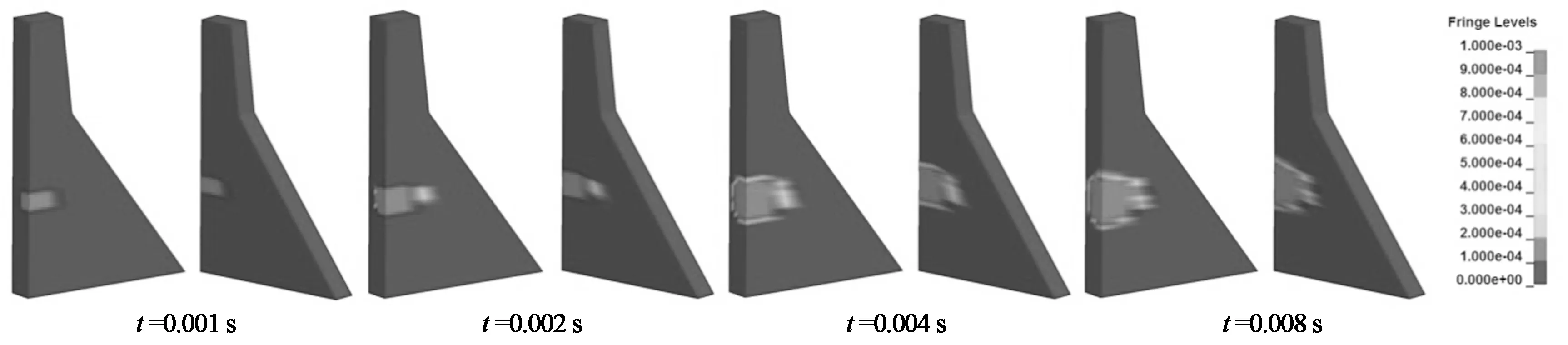
图8给出了炸点1,3,5的正常蓄水位及空库条件下等效塑性应变过程.由图8可看出刚开始爆炸时,大坝坝体产生等效塑性应变,在0~0.004 s增加较快,在0.008 s左右趋于稳定.正常蓄水位条件下接触爆炸的等效塑性应变的分布范围比空库的范围更大,并且随着炸点位置的下移,同样炸药量下对大坝造成的破坏更大(炸点5的等效塑性应变范围最大).
3.3正常蓄水位时上下游接触爆炸时重力坝的抗爆性能分析
为了比较正常蓄水位条件下,上下游不同炸点接触爆炸时对大坝产生的动力响应,在该重力坝的坝顶布置测点A,并分析炸点接触爆炸时测点A处的加速度、速度、位移和压力随时间的变化特点及反应谱分析.由于计算工况较多,且正常蓄水位条件下A测点的加速度、速度、位移、压力的时程变化以及反应谱具有相似性,本文取上游处的炸点1和下游处的炸点6作为比较分析对象,如图5所示.

(a) 正常蓄水位条件

(b)空库条件图7 不同炸点下坝体响应幅值随高程变化曲线Fig.7 Response amplitude as a function of the height of dam subjected to contact explosion at different points
(a)正常蓄水位炸点1的等效塑性应变演变过程

(b)空库炸点1的等效塑性应变演变过程
(c)正常蓄水位炸点3的等效塑性应变过程
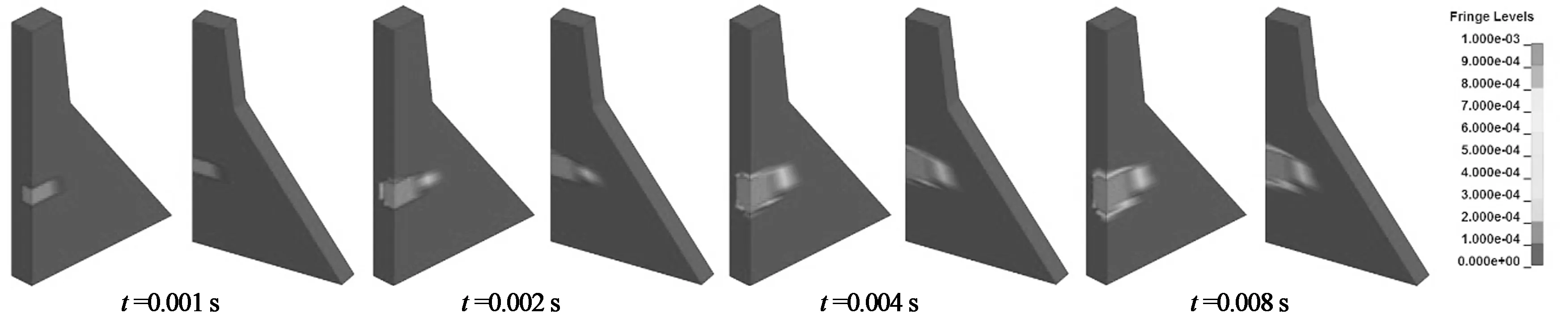
(d)空库炸点3的等效塑性应变演变过程

(e)正常蓄水位炸点5的等效塑性应变过程
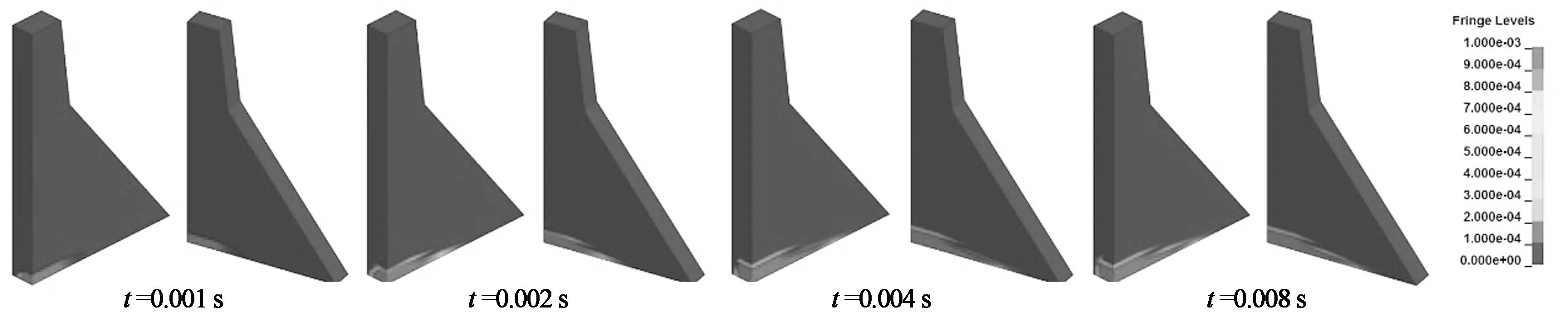
(f)空库炸点5的等效塑性应变过程图8 等效塑性应变过程Fig.8 Time sequences of equivalent plastic strain
3.3.1正常蓄水位时上下游等高程炸点接触爆炸时,同一测点(A测点)的时程分析
图9(a)给出了接触爆炸时A测点顺河向的加速度时程曲线.通过对上下游不同炸点的加速度时程分析可知,上游侧炸点1的最大峰值加速度大于下游侧炸点6的最大峰值加速度约13.5%.正常蓄水位时由于上游侧动水压力的影响,上游侧炸点1接触爆炸后产生的峰值加速度略微滞后,且持续时间也较下游侧炸点6的长,波动幅度也较大.综上所述,大坝在正常蓄水位时,上游侧炸点接触爆炸产生的加速度响应比下游侧炸点接触爆炸产生的加速度响应剧烈.
图9(b)给出了接触爆炸时A测点顺河向的速度时程曲线.通过对上下游不同炸点的速度时程分析可知,上游侧炸点1的最大峰值速度约为下游侧炸点6的最大峰值速度的2.8倍.正常蓄水位时由于上游侧动水压力的影响,上游侧炸点1接触爆炸后产生的峰值速度略微滞后,并且长时间维持在峰值速度附近.综上所述,大坝在正常蓄水位时,上游侧炸点接触爆炸产生的速度响应比下游侧炸点接触爆炸产生的速度响应剧烈得多.
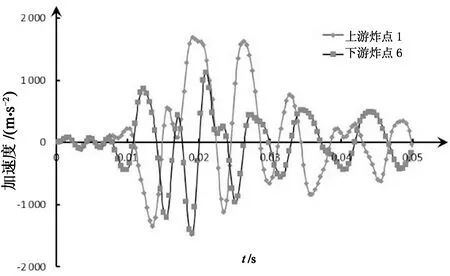
时间/s (a)加速度时程对比
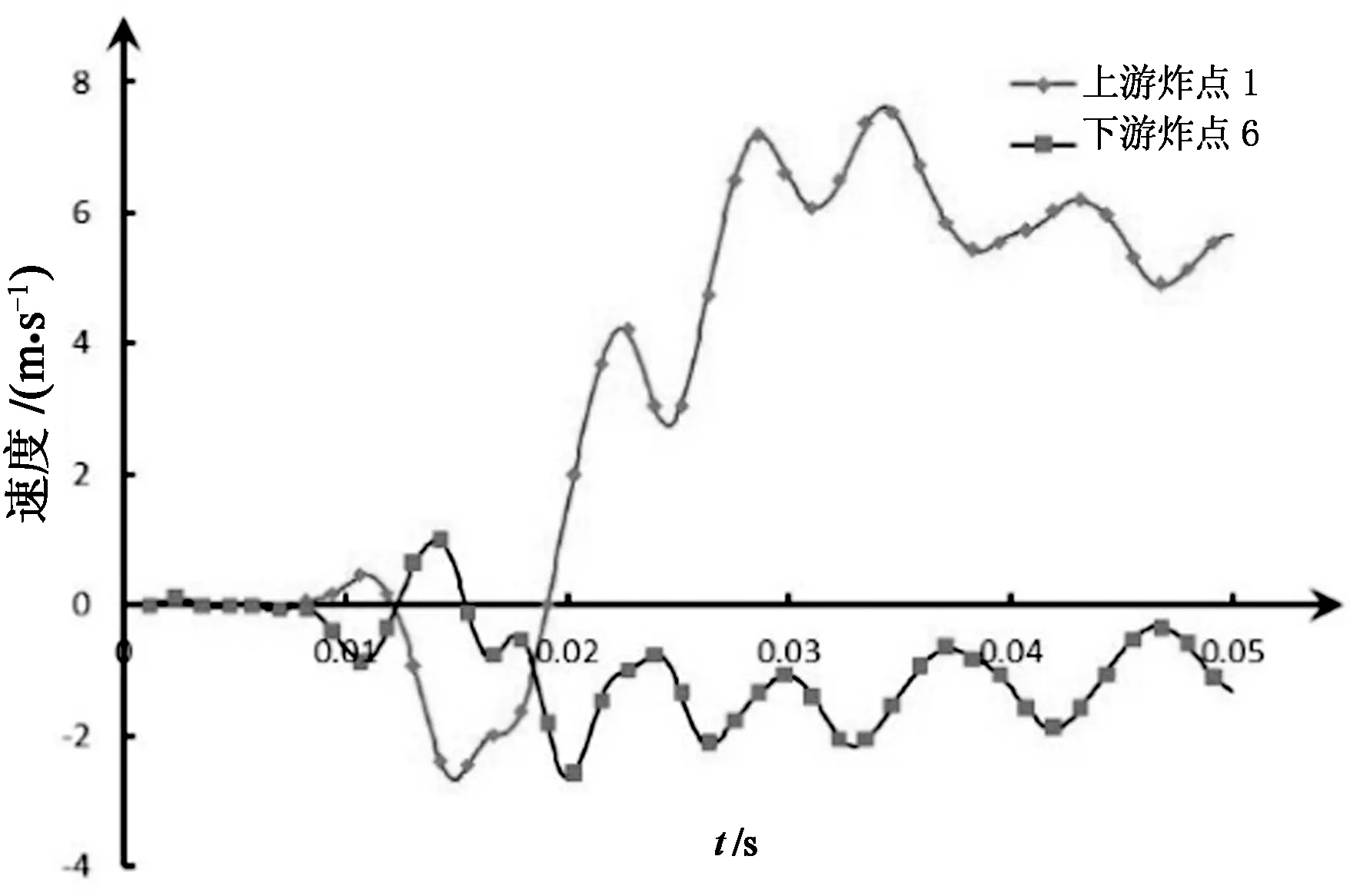
时间/s (b)速度时程对比

时间/s (c)位移对比图9 测点A顺河向时程对比Fig.9 Contrastive analysis of time-histories along the river at point A
图9(c)给出了接触爆炸时A测点的顺河向位移时程曲线.由A测点可知,在正常蓄水位时由于上游侧动水压力的影响,上游侧炸点1接触爆炸后产生的最大位移大大超过下游侧炸点6的最大位移,位移曲线的波动幅度也更大,从而对大坝的破坏也较大.
3.3.2正常蓄水位时上下游等高程炸点接触爆炸时,同一测点(A测点)的反应谱分析
图10(a)所示为接触爆炸时A测点顺河向的加速度反应谱对比图.
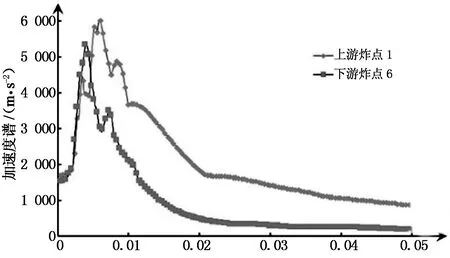
周期/s (a)加速度反应谱对比

周期/s (b)速度反应谱对比
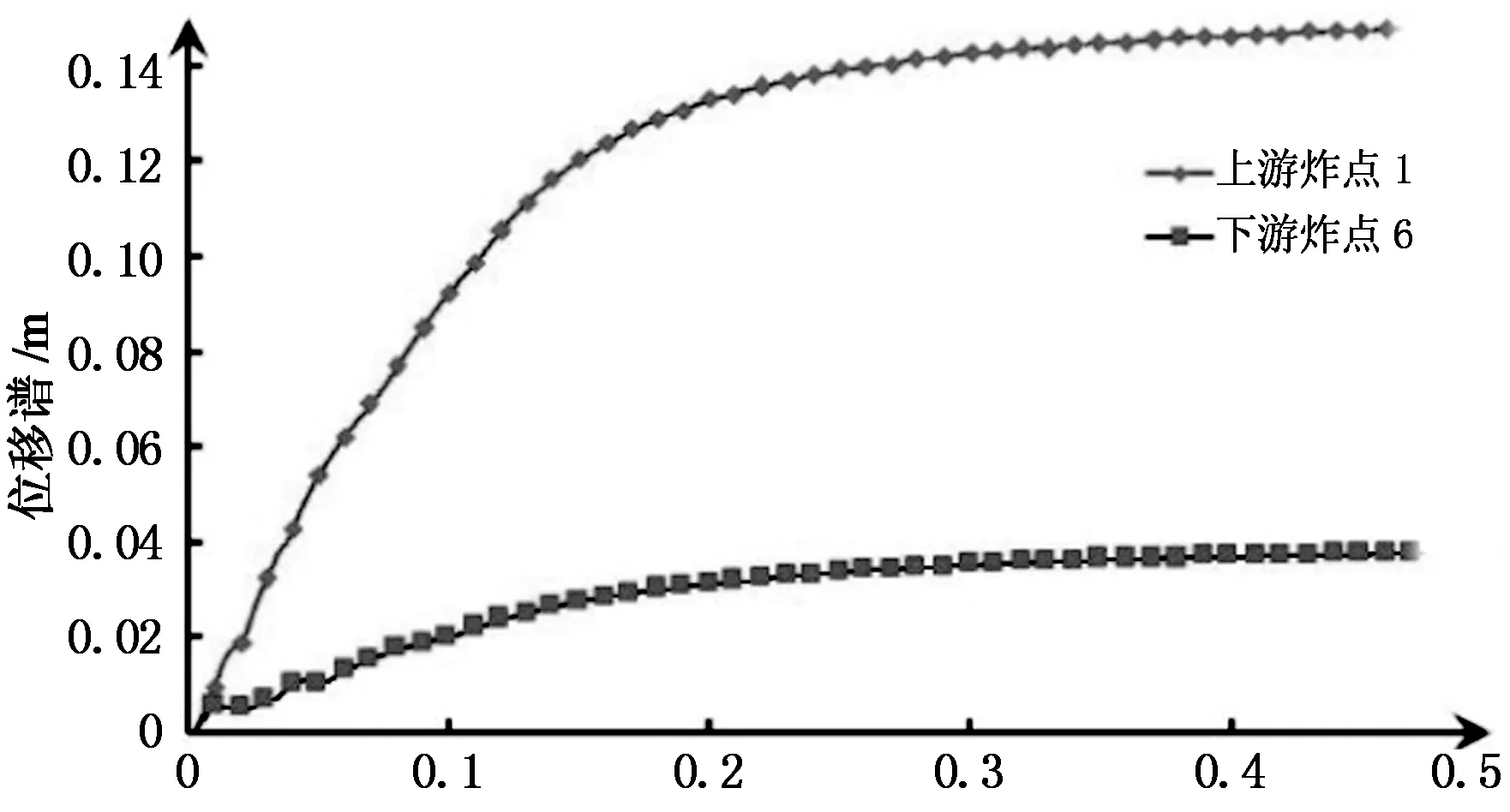
周期/s (c)位移反应谱对比图10 测点A顺河向反应谱对比Fig.10 Contrastive analysis of response spectrum along the river at point A
由图可清晰地看出,加速度反应谱的峰值都很高,无论是上游侧炸点1还是下游侧炸点6均超过了5 000 m/s2.在周期约0.005 s之前,上下游侧炸点接触爆炸产生的加速度谱几乎都是一样的,且下游侧炸点6的加速度谱在周期0.005 s左右达到最大值;在周期约0.005 s之后,下游侧炸点6的加速度谱开始迅速下降至0.02 s后稳定,而上游侧炸点1的加速度谱在周期0.006 s左右达到峰值,随后才开始下降.由于动水压力的影响,上游侧炸点的加速度反应谱峰值较大.综上所述,上下游侧炸点位置影响加速度谱的峰值和所包含周期的范围.上游侧炸点的加速度反应谱整体较下游侧炸点的加速度反应谱大.对固有周期0~0.02 s的加速度敏感的结构影响较大.
图10(b)给出了接触爆炸时A测点顺河向的速度反应谱对比图.由图可清晰地看出,上游侧炸点1速度反应谱的峰值大约是下游侧炸点6速度反应谱峰值的2倍.由于动水压力的影响,上游侧炸点1的速度谱谱值快速增大并在最大速度谱谱值附近上下波动,最终在约6.9 m/s附近稳定;下游侧炸点6的速度谱达到峰值后则快速衰减,最终稳定在2.6 m/s附近.综上所述,上下游侧炸点位置对速度反应谱的峰值产生了较大的影响,使上游侧炸点的速度谱在峰值处有波动,但并未影响两者速度反应谱的谱形,并在周期0.01 s后上游侧炸点接触爆炸产生的冲击波对大坝的速度反应谱起着控制作用,说明对固有周期大于0.01 s的速度敏感的结构影响较大.
图10(c)给出了接触爆炸时A测点顺河向的位移反应谱对比图.由图可清晰地看出,在周期约0.2 s之前,上下游侧炸点接触爆炸产生的位移谱谱值均快速增大;在周期约0.2 s之后,两者均达到最大值并稳定.由于上游侧炸点存在动水压力,上游侧炸点1位移反应谱的峰值大约是下游侧炸点6位移反应谱峰值的3.8倍.综上所述,上下游侧炸点只影响位移谱的峰值,对谱形没有影响,并且0.2 s之后的长周期上游侧炸点接触爆炸产生的冲击波对大坝的位移谱起着控制作用,说明对固有周期大于0.2 s的位移敏感的结构影响较大.
3.3.3正常蓄水位时上下游等高程炸点接触爆炸时的压力传播过程对比
图11(a)给出了上游炸点1水下接触爆炸后冲击波的压力传播过程,在t=0~0.01 s时间内,压力波迅速向坝体四周扩散,逐步扩散到大坝顶端和下游折坡处,可见压力波传到坝顶端和下游折坡处时仍有较大的能量,对大坝坝顶和下游折坡处破坏较大;在t=0.01~0.5 s时间内,爆炸点压力由于动水压力的影响缓慢耗散,而坝头处的压力波能量在空气中快速耗散,下游折坡处的压力波继续沿着下游坝坡表面向大坝坝趾传播,并在传播过程中不断反射,导致在坝趾有较大的压力波能量,对大坝的底部产生很大的压力波集中现象,这和文献[18]的结果相吻合.
图11(b)给出了下游炸点6接触爆炸后冲击波的压力传播过程,在t=0~0.05 s时间内,压力波迅速向坝体四周扩散,压力波能量迅速在坝体和空气中耗散,在t=0.01 s时压力波能量已耗散了大部分,虽然对大坝坝体造成一定的破坏,但没有上游炸点爆炸时造成的破坏范围大,破坏范围主要集中在炸点处.
3.3.4正常蓄水位条件下上下游不同高程炸点接触爆炸时大坝的毁伤特性分析
图12给出了正常蓄水位条件下上游侧炸点1,3,5和下游侧炸点6,8,10等效塑性应变演变过程.由图12可看出刚开始爆炸时,大坝坝体产生等效塑性应变,在0~0.004 s增加较快,在0.008 s左右趋于稳定.正常蓄水位条件下上游侧炸点接触爆炸产生的等效塑性应变的分布范围比下游侧炸点接触爆炸产生的等效塑性应变的分布范围稍大,但并不明显;随着炸点位置的下移,同样炸药量下损伤范围略有增加(炸点5和炸点10的等效塑性应变范围最大).
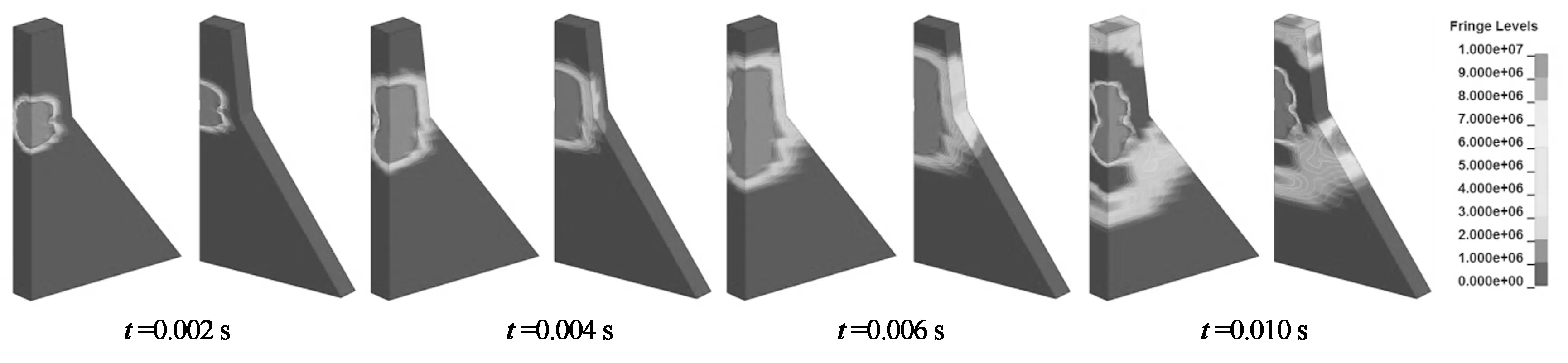
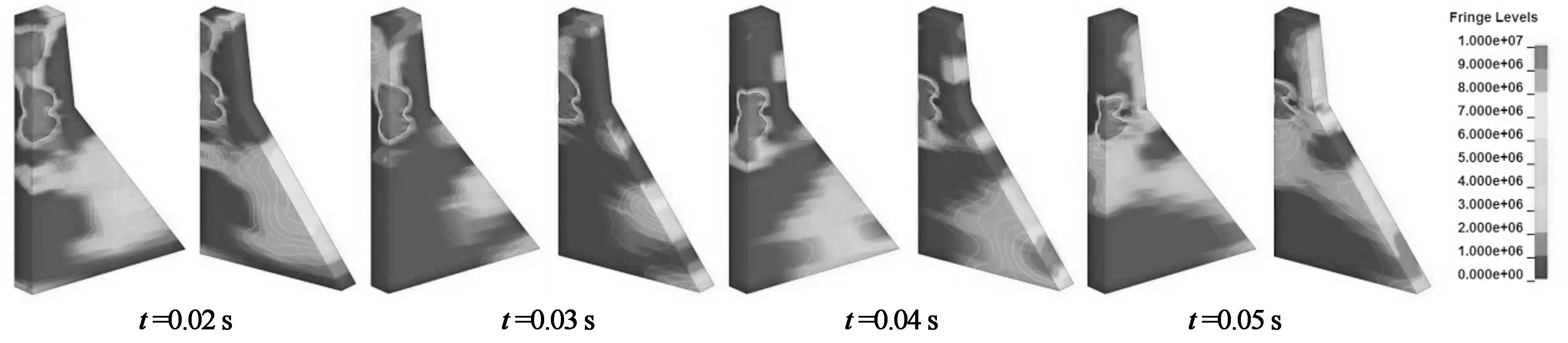
(a) 正常蓄水位上游侧炸点1接触爆炸压力波传播过程(Pa)
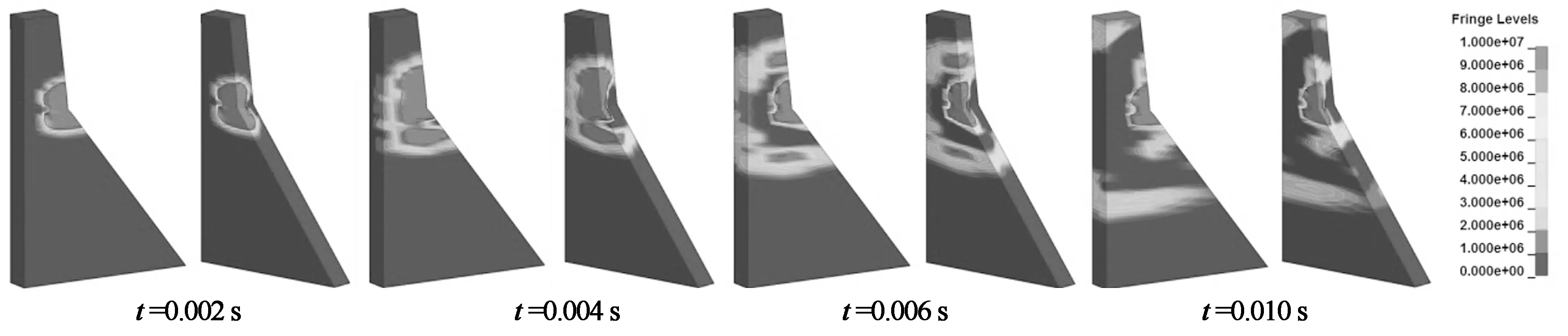

(b) 正常蓄水位下游侧炸点6接触爆炸压力波传播过程(Pa)图11 接触爆炸下冲击波压力传播过程Fig.11 The propagation of pressure wave under contact explosive
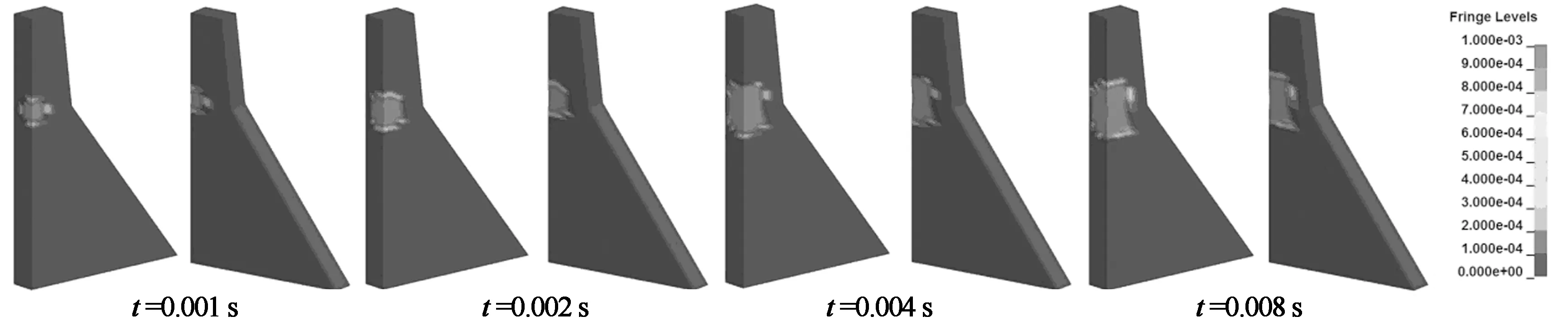
(a)正常蓄水位上游侧炸点1的等效塑性应变演变过程

(b) 正常蓄水位下游侧炸点6的等效塑性应变演变过程
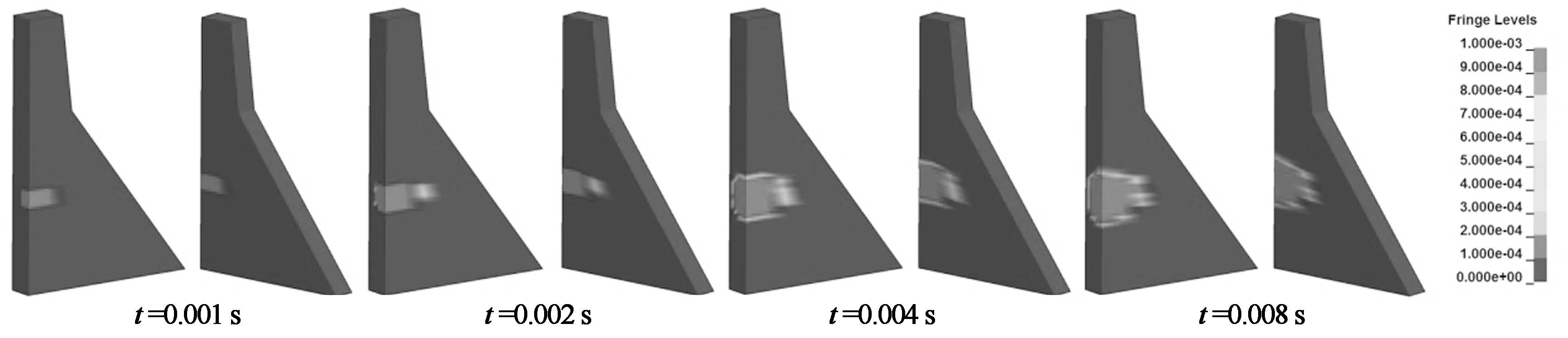
(c) 正常蓄水位上游侧炸点3的等效塑性应变演变过程
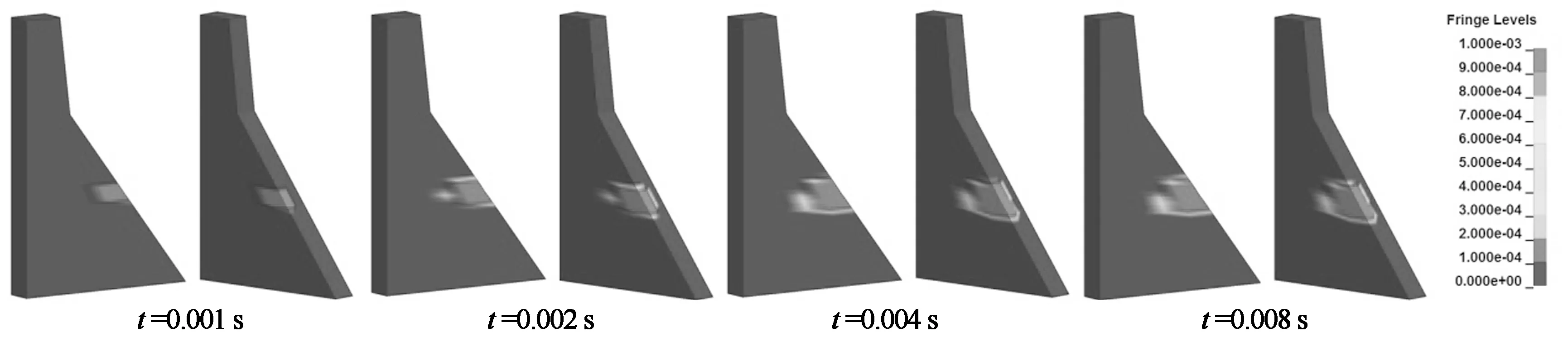
(d) 正常蓄水位下游侧炸点8的等效塑性应变演变过程

(e) 正常蓄水位上游侧炸点5的等效塑性应变演变过程

(f) 正常蓄水位下游侧炸点10的等效塑性应变演变过程图12 等效塑性应变演变过程Fig.12 The propagation of equivalent plastic strain
4 结 论
通过本文对于混凝土重力坝接触爆炸的响应及破坏特性分析,可以得到以下结论:
1) 数值模拟的水下爆炸与长江科学院刘美山等进行的混凝土深水爆炸实验进行对比,模拟结果较为接近,验证了运用显式非线性动力分析程序LS-DYNA模拟混凝土重力坝水下爆炸的稳定可靠性.
2) 通过正常蓄水位与空库条件对比显示:正常蓄水位的动力响应比空库更为剧烈,在速度与位移响应曲线中更为明显,并且由于动水压力的原因,正常蓄水位比空库的时程曲线有滞后.分析不同炸点不同测点的动力响应后可得出,在上游折坡对应的高程处进行水下接触爆炸,坝体产生的加速度、速度及位移响应最大,且随着炸点高程的下移,对大坝毁伤范围也更大.
3) 对比正常蓄水位时上下游不同炸点位置接触爆炸可得出:上游侧炸点动力响应比下游侧炸点更加剧烈,并且上游侧炸点的爆炸冲击波对坝顶、折坡及坝趾均产生了较大的冲击破坏.炸点位置对反应谱的峰值起决定作用.
[1]GEORGIN J F,REYNOUARD J M . Modeling of structures subjected to impact:concrete behavior under high strain rate[J]. Cement & Concrete Composites,2003,25(1):131-143 .
[2]ZHANG Q,LIN D C,BAI C H. Correlations of blast damage to ground surface targets with explosion seismic effect[J]. Soil Dynamics and Earthquake Engineering,2004,24(7):519-525.
[3]陆路,李昕,周晶.水下爆炸引起的混凝土坝危险性估计[J]. 水资源与水工程学报,2010,21(5):6-9.
LU Lu,LI Xin,ZHOU Jing. Risk analysis of high concrete dam result from underwater explosion[J].Journal of Water Resources & Water Engineering,2010,21(5):6-9.(In Chinese)
[4]LIU M B, LIU G R . Smoothed particle hydrodynamics(SPH):an overview and recent developments[J]. Archives of Computational Methods in Engineering,2010,17 (1):25-76 .
[5]张社荣,孔源,王高辉,等. 混凝土重力坝水下接触爆炸下的毁伤特性分析[J]. 水利学报,2014,45(9):1057-1065.
ZHANG She-rong,KONG Yuan,WANG Gao-hui,etal. Damage characteristic analysis of concrete gravity dams subjected to underwater contact explosion[J]. Journal of Hydraulic Engineering,2014,45(9):1057-1065.(In Chinese)
[6]张社荣,王高辉. 混凝土重力坝抗爆性能及抗爆措施研究[J]. 水利学报,2012,43(10):1202-1213.
ZHANG She-rong,WANG Gao-hui. Study on the antiknock performance and measures of concrete gravity dam[J]. Journal of Hydraulic Engineering, 2012,43(10):1202-1213.(In Chinese)
[7]李本平. 制导炸弹连续打击下混凝土重力坝的破坏效应[J]. 爆炸与冲击,2010,30(2):220-224.
LI Ben-ping. Damage effect of a concrete gravity dam under continuous attacks of guided bombs [J]. Explosion and Shock Waves, 2010, 30(2):220-224. (In Chinese)
[8]YU T T. Dynamical response simulation of concrete dam subjected to underwater contact explosion load[C] //Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering. Los Angeles:IEEE,2009:769-774.
[9]徐俊祥,刘西拉. 水中爆炸冲击下混凝土坝动力响应的全耦合分析[J]. 上海交通大学学报,2008,42(6):1001-1004.
XU Jun-xiang,LIU Xi-la. Full coupled simulation of concrete dams subjected to underwater explosion[J]. Journal of Shanghai Jiaotong University,2008,42(6):1001-1004.(In Chinese)
[10]张社荣,王高辉. 浅水爆炸冲击荷载下高拱坝抗爆性能分析[J].天津大学学报:自然科学与工程技术版,2013,46(4):315-321.
ZHANG She-rong,WANG Gao-hui. Antiknock performance of high arch dam subjected to shallow water explosion [J]. Journal of Tianjin University: Science and Technology,2013,46(4):315-321.(In Chinese)
[11]张社荣,杨明,王高辉. 水下爆炸冲击下重力拱坝的破坏特性[J]. 水电能源科学,2014,32(7):69-73.
ZHANG She-rong,YANG Ming,WANG Gao-hui. Failure characteristics of gravity arch dam subjected to underwater explosion[J].Water Resources and Power,2014,32(7):69-73.(In Chinese)
[12]刘军,刘汉龙,张正. 爆炸荷载下土石坝动力响应特征的数值模拟[J]. 防灾减灾工程学报,2010,30(1):10-16.
LIU Jun,LIU Han-long,ZHANG Zheng. Numerical simulation of dynamic response of an earth and rock-fill dam to a blast loading[J]. Journal of Disaster Prevention and Mitigation Engineering,2010,30(1):10-16.(In Chinese)
[13]宋娟,李术才,张敦福.基于不同算法和边界条件的土中爆炸数值模拟[J]. 爆破,2014,31(2):21-25.
SONG Juan,LI Shu-cai,ZHANG Dun-fu. Numerical simulation of explosion in soil under various arithmetic and boundary conditions[J]. Blasting,2014,31(2):21-25.(In Chinese)
[14]童桦,程红梅,罗松南. 预应力损伤混凝土介质中波的传播[J]. 湖南大学学报: 自然科学版, 2005,32(1): 48-51.
TONG Hua,CHENG Hong-mei,LUO Song-nan. Wave propagation in prestressed concrete with damage[J]. Journal of Hunan University: Natural Sciences, 2005,32(1):48-51.(In Chinese)
[15]罗松南,程红梅. 波在局部损伤混凝土介质中的传播[J]. 湖南大学学报:自然科学版, 2002,29(2): 20-23.
LUO Song-nan,CHENG Hong-mei. Propagation of waves in concrete media with local damage[J]. Journal of Hunan University: Natural Sciences, 2002,29(2):20-23. (In Chinese)
[16]COLE R H. Underwater explosion[M]. New Jersey: Princeton University Press, 1948:118-127.
[17]李建阳. 爆炸载荷下水中混凝土损伤破坏规律研究[D]. 合肥:中国科学技术大学工程科学学院, 2010:40-52.
LI Jian-yang. Research on the damage and fracture rules of concrete in water due to explosion loading[D]. Hefei: School of Engineering Science, University of Science and Technology of China, 2010:40-52. (In Chinese)
[18]崔杰.近场水下爆炸气泡载荷及对结构毁伤试验研究[D].哈尔滨:哈尔滨工程大学船舶工程学院,2013:184-186.
CUI Jie. Experimental study on underwater explosion bubble loads and damage on the structure[D]. Harbin :College of Shipbuilding Engineering, Harbin Engineering University,2013:184-186.(In Chinese)
Study on the Response and Damage Characteristic of Concrete Gravity Dam Subjected to Contact Explosion
XU Qiang, CAO Yang, CHEN Jian-yun†, LI Jing, LIU Jing
(Faculty of Infrastructure Engineering, Dalian Univ of Technology, Dalian, Liaoning116024,China)
In this study, an explicit non-linear analysis program of LS-DYNA was employed to simulate a concrete gravity dam with either normal or empty reservoir under contact explosion. Considering the effect of high strain rate of concrete under the contact explosion, HJC (Holmquist-Johnson-Cook) constitutive model was adopted to simulate the damage characteristic and plastic deformation of the dam. Firstly, “Explosive-Air-Water-Concrete Test Cube” model was constructed and verified. “Explosive-Air-Water Storage-Dam-Foundation” dynamic full coupled model was then developed to evaluate the dynamic response and damage characteristic of the concrete gravity dam under the contact explosion denoted by TNT explosive on both normal water level dam and empty dam. The test shows that the analytical method is reliable to study the contact explosion of the concrete gravity dams, and it also covers the shortage of experimental study. In the case of the normal water level, the dynamic response and the damage of the dam are greatly affected by the explosion points in upstream. Therefore, the study of anti-explosion properties for the concrete gravity dam should focus on the damage measurement when the explosion points are disposed in upstream under the normal water level.
concrete gravity dams; HJC constitutional model; underwater contact explosion; response; damage characteristics
1674-2974(2016)07-0062-13
2015-08-20
国家自然科学基金重点资助项目(51138001,51178081),Key Program of National Natural Science Foundation of China(51138001,51178081); 国家重点基础研究发展计划(973计划)资助项目(2013CB035905);中央高校基本科研业务费专项资金资助项目(DUT15LK34,DUT14QY10); 辽宁省重点实验室基础研究项目(LZ2015022)
徐强(1982-),男,辽宁大连人,大连理工大学副教授,博士
†通讯联系人,E-mail:eerdool@dlut.edu.cn
TV331
A

