预应力混凝土钢组合风电塔架塔段优化研究*
许 斌,李泽宇,陈洪兵
(1. 湖南大学 土木工程学院,湖南 长沙 410082;2. 湖南大学 工程结构损伤诊断湖南省重点实验室,湖南 长沙 410082)
预应力混凝土钢组合风电塔架塔段优化研究*
许斌1,2†,李泽宇1,陈洪兵1
(1. 湖南大学 土木工程学院,湖南 长沙410082;2. 湖南大学 工程结构损伤诊断湖南省重点实验室,湖南 长沙410082)
以某2 MW传统钢筒结构风电塔架为对象,采用预应力混凝土-钢组合塔架结构取代原钢筒结构,并对组合塔架结构的两塔段进行优化.以造价为目标函数, 在塔架几何外形不变的情况下,考虑预应力混凝土与钢塔段的强度、刚度、稳定性、疲劳以及自振频率、顶部最大位移等约束条件, 借助改进的粒子群优化算法,对预应力混凝土和钢塔段的高度及其截面尺寸进行优化.结果表明,采用粒子群算法对预应力混凝土-钢组合塔架两个塔段进行优化后,在满足各项约束条件的前提下,组合塔架结构形式的造价比传统钢塔架造价降低约27%.
组合风电塔架;结构优化;改进的粒子群算法;钢筒风电塔架
风能作为一种蕴藏丰富,分布广泛,而且清洁的可再生能源,受到了全世界越来越多的关注[1-2].近年来我国风电场建设发展迅速.对于我国能源相对短缺的湖南、贵州、云南等南方省份,风资源大多分布在交通不便的山区.风电塔架作为水平轴风力发电机组的下部支撑,是风机的重要组成部分.兆瓦级传统钢结构风电塔筒的底截面直径一般超过4 m,接近一些国家公路运输容许的最大宽度和高度,因此传统钢塔筒的运输非常困难,而且运输费用高.特别是南方山区风场建设中,重量大、长度长的钢制塔筒的运输越发困难而且危险性高.此外为了建设上山道路必须花费大量额外资金,大大增加了风电场建设的成本.
由于混凝土结构可以现浇或者预制,因此采用钢筋混凝土或者预应力混凝土代替部分钢结构,形成钢筋混凝土或者预应力混凝土-钢组合风电塔筒结构是有效的解决之道.Singh等的研究表明预应力钢筋混凝土风电塔架的设计比全钢塔架具有更大的灵活性[3].Seidel对已经建成的钢-混凝土组合塔架和钢塔架整体结构进行了结构比较分析,说明钢-混凝土组合塔架可以克服山区交通不便、难以运输的问题[4].牛家兴对预应力混凝土与钢组合塔架的研究表明,预应力混凝土与钢组合塔架克服了传统钢管塔的运输及制造困难,同时也能更好地满足目前风机功率大型化发展趋势对于塔架高度的需求,代表了未来风电结构发展的方向[5].许斌等提出了一种新型的嵌入式开孔板和穿孔钢筋连接段结构方案,有效地提高了塔架过渡段刚度并改善了应力分布[6].这种组合塔架中预应力混凝土段与钢结构段的高度以及各自的界面尺寸的优化对于降低造价,保证其良好的动静力性能具有重要意义.
Uys等以造价为目标函数对传统钢塔架结构进行了优化[7].然而,目前对于预应力混凝土与钢组合塔架中钢塔段与混凝土塔段的高度的比例以及各段的截面尺寸的优化尚无详细研究[8-9].Hani 等基于风电塔架的自振周期以及稳定性设计提出了5种优化准则并对某100 kW风机进行了优化设计[10].国内,马宏旺等提出了一种基于ABAQUS和遗传算法的预应力混凝土塔架优化方案[11].陈俊岭等提出了一种新的塔架结构形式并对其进行了优化[12].
本文以某兆瓦级风力发电机组的传统钢塔架为对象,采用预应力混凝土-钢组合风电塔架结构方案,考虑不同风荷载工况下,以强度、刚度和稳定性为约束条件,以造价为目标函数,对预应力混凝土段和钢塔段的高度以及各段的界面尺寸采用粒子群优化算法(Particle Swarm Optimization, PSO)进行优化.两塔段高度的优化结果与国外文献报道的预应力混凝土-钢组合塔架工程实例吻合较好[9].
1 预应力混凝土-钢组合塔架结构优化约束条件
风电塔筒所受荷载均为偏心荷载,风荷载作为风机塔架设计的重要荷载之一[13],由于其不确定性,根据相关设计规程规定,需要对4种不同风速(平均风速、额定风速、切出风速以及暴风风速)下的塔筒受力进行计算.结构设计必须满足钢塔架以及预应力混凝土塔段的强度、刚度和稳定性要求.本文以强度、刚度和稳定性作为约束条件进行结构的优化求解.
1.1钢筒段约束条件
1.1.1局部稳定
由烟囱设计规范[14],钢筒段局部稳定约束条件可表示为:
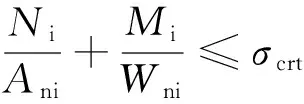
(1)
式中:Mi为塔架水平计算截面的最大弯矩设计值;Ni为相应轴向压力或轴向拉力设计值;Ani为计算截面处的净截面面积;Wni为计算截面处的净截面抵抗矩;ft为钢材抗拉、抗压和拉弯强度设计值;σcrt为塔架筒壁局部稳定的临界应力值;i表示塔架i截面.
1.1.2整体稳定
由钢结构设计规范[15],钢筒段整体稳定约束条件可表示为:

(2)
式中:Abi为计算截面处的毛截面面积;等效弯矩系数βmx=1.0;Wbi为计算截面处的毛截面抵抗矩;λ为塔架长细比, 塔架可以按照悬臂梁构件计算;φ为塔架截面轴心受压构件稳定系数;NEx为欧拉临界荷载.
1.1.3强度
参考ASCE/AWEA RP2011[16],确定塔筒筒壁的各项强度约束条件.
1)抗压强度
fu≤φcFn.
(3)
(4)
Fn=Fcr;
(5)
φc=0.9;
(6)
(7)
式中:D为塔筒外径;t为塔筒壁厚;E为弹性模量;Fy为钢材屈服强度.
Q=0.038E/[Fy(D/t)]+2/3;
(8)
λ1=0.11E/Fy;
(9)
λ2=0.357E/Fy;
(10)
λmax=330.
(11)
2)抗剪强度
fvu≤φvFvn.
(12)
其中,
fvu=Vu/Av,
(13)
Vu为剪力设计值,Av为塔筒截面面积的一半;
Fvn=Fcr;
(14)
φv=0.9;
(15)
(16)
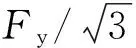
3)抗扭强度
fTu≤φTFTn.
(17)
其中,fTu=Tu/Wt,
(18)
Tu为扭转弯矩设计值,Wt为抗扭截面模量;
FTn=Fcr;
(19)
φT=0.9;
(20)
(21)
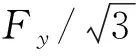
4)综合作用
fvu/(φvFvn)+fTu/(φTFTn)≤1,
(22)
且若fTu/(φTFTn)≤0.2,则有:
fu/(φcFn)≤1.
(23)
若fTu/(φTFTn)>0.2,则有:
[fu/(φcFn)]2+[fvu/(φvFvn)+fTu/(φTFTn)]2≤1.
(24)
1.1.4疲劳
钢塔段的疲劳约束条件为

(25)
式中:Δσe为常幅等效应力幅,可以根据风场气象资料,通过Miner 线性积累损伤法则和雨流计数法统计得出;[Δσ]为容许应力幅,可通过钢结构设计规范[15]查得疲劳参数C,n和β求得.
1.2预应力混凝土塔段约束条件
预应力混凝土段的约束条件主要是对混凝土段承载能力进行验算.根据高耸规范[17],混凝土塔筒筒壁厚t的最小值为tmin=100+0.01D,且不小于180 mm.1.2.1混凝土段约束条件
1)混凝土轴向应力
根据高耸结构设计规范[17],混凝土轴向应力由式(26)确定:
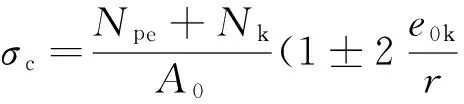
(26)
式中:Nk为各项荷载标准值共同作用下的截面轴向力;Npe为有效预应力;A0为计算截面处混凝土塔筒的水平截面的换算截面面积;e0k为轴向力对界面圆心的偏心距.
对于混凝土段,要求混凝土轴向应力满足以下条件:
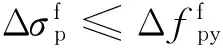
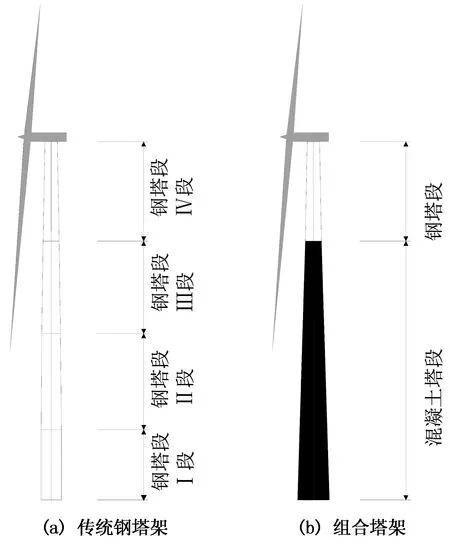
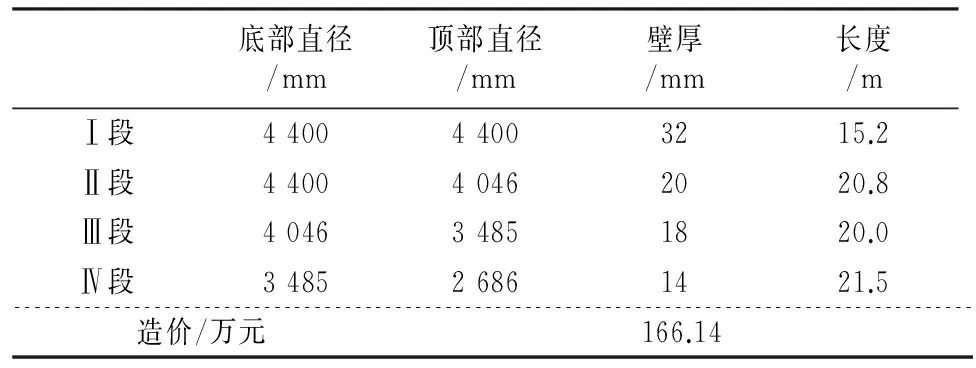
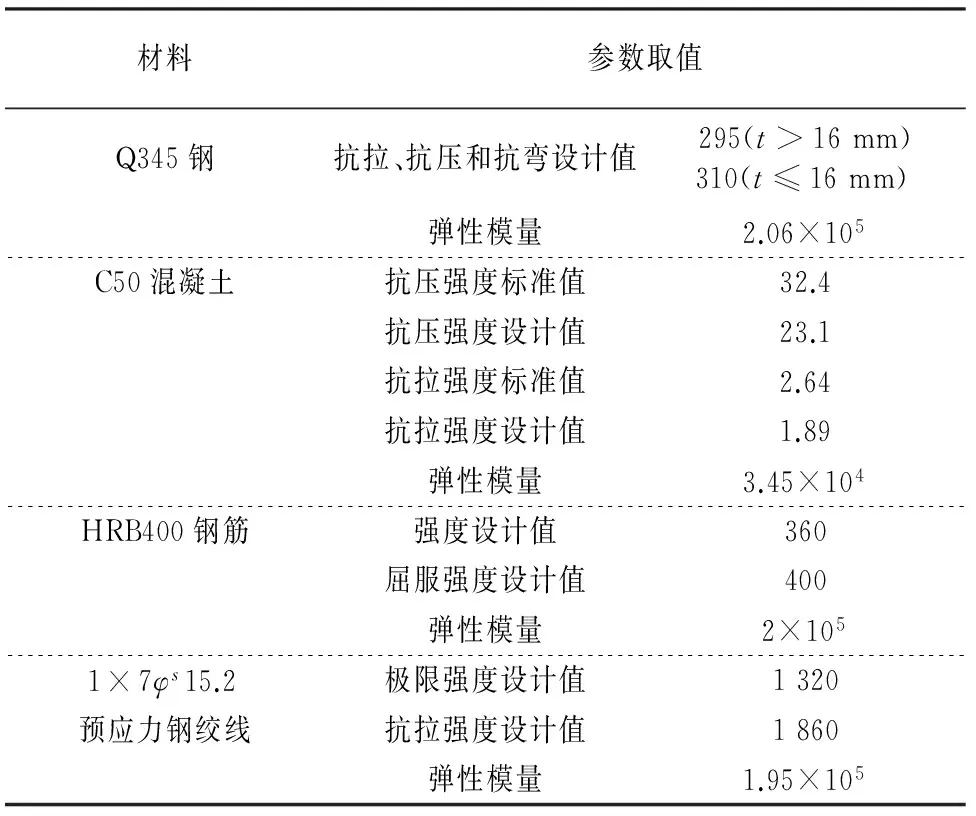
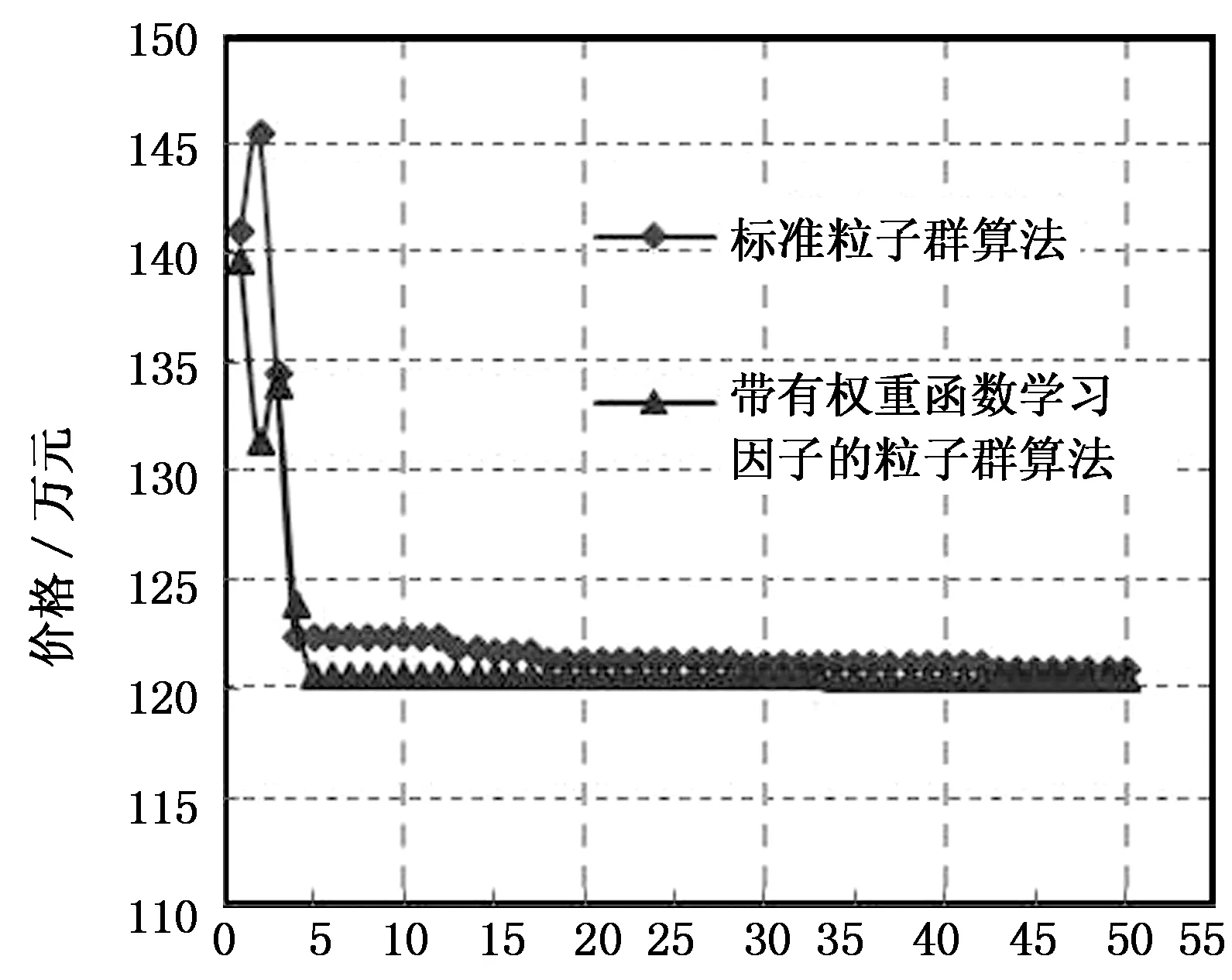
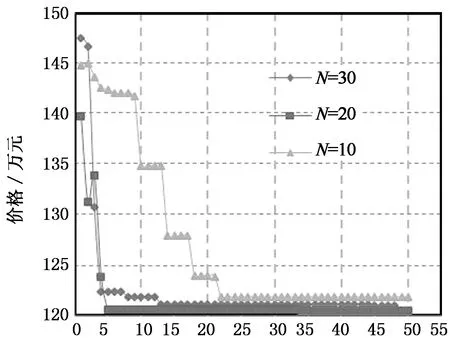
0<σc (27) 式中:fc为混凝土的轴心抗压强度. 2)混凝土截面弯剪扭作用 根据混凝土结构设计规范[18],混凝土截面在弯剪扭作用下需要满足以下条件: (28) 式中:ft为混凝土的轴心抗拉强度;Np0为计算截面上混凝土法向预应力等于零时的预加力. 3)疲劳作用 混凝土规范[18]中对疲劳验算给出了相关规定,要求不出现裂缝的预应力混凝土受弯构件其正截面的混凝土、纵向预应力筋应力幅应符合下列要求: (29) (30) 1.2.2塔筒混凝土-钢连接段 风电塔筒混凝土-钢连接段设计需要考虑多种因素.一方面,连接段需要有良好的传力性能;另一方面,连接段本身需要有足够的强度、刚度以及稳定性. 对于一般的预应力混凝土结构,涉及到钢筋的绑扎和定位、混凝土浇筑等问题,工作量很大.在国外,混凝土塔筒等结构常采用体外预应力混凝土[19].体外预应力混凝土的预应力筋套管布置简单,调整容易,简化了后张法的操作程序,大大缩短了塔筒的施工时间;同时由于预应力筋布置于混凝土外,混凝土浇筑方便,减少了摩擦损失且可以方便地在结构使用过程中更换预应力筋.本文根据截面弯矩设计值,在保证截面混凝土不出现拉应力的原则下,确定截面总预应力水平.预应力筋取36束高强低松弛钢绞线,每一束有8根1×7φs15.2钢绞线,张拉控制应力为1 302 MPa. 1.3塔筒整体约束条件 塔筒整体约束条件主要有自振频率和塔筒的顶部最大位移. 1)自振频率 为了防止塔架与叶片发生共振,塔架动力特性尤为重要.一般要求风电塔架的固有频率应避开风机的叶片转动频率以及叶片通过频率这两个区段且至少相差10%[19].如图1所示,塔筒自振频率应处于白色区域内. 图1 塔架自振频率要求Fig.1 Natural frequency constraints of tower 2)塔筒顶部最大位移 塔筒顶部最大位移应满足下式要求.[10] Wmax/Wal<1. (31) 式中:Wmax为塔筒顶部的最大位移;Wal为塔筒顶部最大容许位移. 1.4荷载组合 参考荷载规范[20],塔架荷载组合见表1,其中DL为永久荷载,TWL为风轮气动荷载,WL为塔架风荷载,PL为俯仰荷载,EL为附加荷载. 取塔筒造价为优化目标函数. 2.1钢塔段材料价格计算 钢塔段造价可以表示为: (32) 式中:F1为钢塔筒材料价格;C1为市场钢制塔筒的平均价格; r为钢筒半径;ti(i=1,2,3,…,N)为各段钢筒壁厚;hi(i=1,2,3,…,N)为各段钢筒长度;N为法兰数量(即钢筒数量);C为单个法兰造价. 表1 荷载组合 2.2混凝土塔筒段价格计算 由普通钢筋和预应力钢绞线的用量,塔筒混凝土段造价可表示为: C4ρsAph4. (33) 式中:F2为混凝土塔筒材料价格;C2,C3,C4分别为C50混凝土、普通钢筋、预应力钢绞线的市场平均价格;r为混凝土塔筒半径;t为混凝土塔筒壁厚;h4为混凝土塔筒高度;As,Ap分别为普通钢筋和预应力钢筋的面积. 2.3其他费用 法兰造价、模版、脚手架、人工费、机械费、管理费、措施费、规费等费用根据《湖南省建筑工程单位估计表(99)》《湖南省建筑工程概算定额(2001)》《湖南省建筑装饰装修工程消耗量标准(2006)》和各类材料在湖南地区的基本价格进行估价得到.运输、道路建设等其他方面的费用受工程地点等因素影响较大,难以估算,本文暂未考虑. 目标函数和约束方程都是非线性的,其优化问题可以表示为: (34) 式中:z为目标函数;x=(x1,x2,…,xn)T为向量;c(x)=[h1(x),h2(x),…,hn(x)]T为函数向量;f(x)为标量函数;f(x)和c(x)为非线性函数. 基本粒子群算法由于采用常数学习因子和惯性权重,寻优结果往往不够理想.此外,所有粒子都使用相同的学习因子和惯性权重来更新速度和位置并朝这个最优粒子聚集,容易陷入局部最优解,且收敛速度较慢.因此,本文采用了带有权重函数学习因子的粒子群算法进行优化求解[21].其学习因子和惯性权重的计算公式为: (35) 式中:t为迭代次数;M为最大迭代次数;wmax为最大惯性权重;wmin为最小惯性权重;c1为学习因子1;c2为学习因子2.本文利用MATLAB进行编程,主程序为粒子群算法.先随机生成代表设计变量的粒子送入f(x)中计算在满足所有约束条件下的塔筒造价,即目标函数,然后将每个粒子的目标函数值返回主程序,用每组设计变量对应的造价通过更新原则即式(32)更新学习因子和惯性权重,得到新的粒子的速度和位置.之后,将新粒子送入f(x)中计算造价,多次循环后得出满足结束条件时的最优造价[22].粒子群算法流程图如图2所示. 图2 粒子群算法流程图Fig.2 Flow chart of PSO 在选择设计变量时, 为减少循环次数, 提高计算效率, 依据工程中的设计经验,对设计变量的取值范围进行限定.本文优化变量及取值范围见表2. 表2 设计变量取值范围 本文以湖南某山区2 MW风机塔筒为研究对象.该风机塔架原设计为全钢筒设计,现拟更改为预应力混凝土-钢组合塔架结构形式.全钢筒塔架结构与预应力混凝土-钢组合塔架结构的对比图见图3.原钢塔架设计由4段钢塔段组成,总高为77.5 m,如图3(a)所示,现使用预应力混凝土-钢组合风电塔架将原设计全钢制塔架下部整体替换为预应力混凝土塔段,如图3(b)所示.原钢塔筒设计具体参数见表3. 图3 传统钢塔架和组合塔架Fig.3 Steel tower and hybrid tower表3 钢塔筒原设计参数Tab.3 Original design parameters of steel tower 底部直径/mm顶部直径/mm壁厚/mm长度/mⅠ段440044003215.2Ⅱ段440040462020.8Ⅲ段404634851820.0Ⅳ段348526861421.5造价/万元166.14 结合《烟囱设计规范》[14]《钢结构设计规范》[15]《高耸结构设计规范》[17]《混凝土结构设计规范》[18]和厂家提供的风电场荷载等条件,基于上文所述目标函数和约束条件,对组合塔筒预应力混凝土段与钢塔段的高度以及两塔段的截面尺寸进行优化.组合塔架的材料参数取值见表4. 表4 组合塔架材料参数 首先,对采用不同优化算法的优化过程进行对比.其中,带有权重函数学习因子的粒子群算法各参数取值分别为:最大惯性权重wmax=0.9;最小惯性权重wmin=0.4;粒子数目N=30;迭代次数M=50.标准粒子群算法的进化各参数取值分别为:学习因子1取c1=2;学习因子2取c2=2;惯性权重w=0.5;粒子数目N=30;迭代次数M=50.运输时,钢塔筒最大长度为25 m. 图4表示的是相同条件下带有权重函数学习因子的粒子群算法与标准粒子群算法的进化曲线对比.可见,可变权重和变化的学习因子的粒子群算法收敛更快. 迭代次数图4 改进的PSO算法和PSO算法的 进化曲线的对比Fig.4 Evolution curve comparison of improved PSO and standrad PSO 图5表示的是相同算法条件下不同粒子数的粒子群算法的进化曲线对比.粒子数N=20与N=30时,进化到15代以内,造价即接近最小值.粒子数N=20与N=30时的计算结果区别不大,为提高计算速度,实际计算时粒子数可只取N=20. 迭代次数图5 不同粒子数的粒子群算法的进化曲线对比Fig.5 Evolution curve comparison of PSO with different partical number 表5表示经过优化之后的两塔段高度以及塔筒截面尺寸的优化结构以及相应造价.与原造价约166万元对比可以看出,经过粒子群优化后,造价最终可节省约27%,可以有效减少工程投资.钢筒段长度占塔架全长约30%,与国外现有文献中报道的钢塔段高度占26%的结果较为接近[4,9].考虑到我国与国外在建造费用特别是人工费上的区别,这一比值可以认为是合理的. 表5 组合塔架高度以及截面优化结果 本文采用改进的粒子群算法,对预应力混凝土-钢组合风电塔架的结构塔段高度以及截面尺寸进行优化,综合考虑组合塔架结构的强度、刚度和稳定性等约束条件,以造价为目标函数,通过优化得到了预应力混凝土塔段与钢塔段两段塔架高度以及界面尺寸的优化结果.通过本文的优化算例,可以得出以下结论: 1)带有权重函数学习因子的粒子群算法计算速度快于标准粒子群算法.对于本文组合塔架结构,实际计算时粒子数可只取N=20.对于预应力混凝土-钢组合塔架结构的优化问题,通过修正学习因子和权重可以提高优化计算的精度及效率. 2)通过本文的优化算法得出的预应力混凝土-钢组合塔筒中预应力混凝土塔段的高度约为总塔高的70%,与国外文献报道结果较为接近. 3)采用预应力混凝土-钢组合风电塔架结构代替传统钢结构塔筒,通过优化可以明显降低塔架的造价.优化方案能够有效地减少造价约27%.如果考虑采用预应力混凝土结构后,混凝土的现场浇筑或者预制对道路运输的要求大为降低,可以进一步降低道路建设费用,对山区风场建设可以带来进一步的经济效益.本文暂未考虑塔架抗震等因素对塔架结构的影响,需要进一步开展研究. [1]罗如意, 林晔, 钱野. 世界风电产业发展综述[J]. 可再生能源, 2010,28(2): 14-17. LUO Ru-yi, LIN Ye, QIAN Ye. The development and prospects of world wind power industry[J]. Renewable Energy Resources, 2010,28(2): 14-17. (In Chinese) [2]JACOBSON M Z, DELUCCHI M A. Providing all global energy with wind, water, and solar power, Part I: technologies, energy resources, quantities and areas of infrastructure, and materials[J]. Energy Policy, 2011, 39(3): 1154-1169. [3]SINGH A N. Concrete construction for wind energy towers[J]. The Indian Concrete Journal, 2007, 81: 43-49. [4]SEIDEL M. Experiences with two of the world’s largest wind turbine towers[C]//2003 EWEC European Wind Energy Conference and Exhibition. Madrid: EWEA , 2003: 16-19. [5]牛家兴.预应力混凝土-钢组合风电塔架结构性能研究[D].长沙:湖南大学土木工程学院,2014:9-11. NIU Jia-xing. Research on the structural performance of pretressed concrete-steel hybrid wind turbine tower [D]. Changsha: College of Civil Engineering, Hunan University, 2014:9-11. (In Chinese) [6]许斌,谢咏剑,李正超.预应力砼-钢组合风电塔架穿筋连接段弹塑性分析[J]. 可再生能源, 2015, 33(7):1033-1041. XU Bin, XIE Yong-jian, LI Zheng-chao.Elasto-plastic analysis on a perfobond strip connection of prestressed concerete-steel hybrid wind turbine tower[J]. Renewable Energy Resources, 2015, 33(7) :1033-1041. (In Chinese) [7]UYS P E, FARKAS J, JARMAI K,etal. Optimisation of a steel tower for a wind turbine structure[J]. Engineering Structures, 2007, 29(7): 1337-1342. [8]LANIER M W. LWST phase Ⅰ project conceptual design study: evaluation of design and construction approaches for economical hybrid steel/concrete wind turbine towers [R]. Golden, CO(US): National Renewable Energy Lab, 2005:4-14. [9]SEIDEL M. Auslegung von hybridturmen fur windenergieanlagen [J]. Beton- und Stahlbetonbau, 2002,97(11):564-575. [10]HANI M N,KARAM Y M.Structural design optimization of wind turbine towers[J].Computers and Structures,2000,74: 649-666. [11]MA Hong-wang, MENG Ran. Optimization design of prestressed concrete wind-turbine tower[J]. Science China Technological Sciences, 2014, 57(2): 414-422. [12]陈俊岭,阳荣昌,马人乐.大型风电机组组合式塔架结构优化设计[J]. 湖南大学学报:自然科学版, 2015, 42(5): 29-35. CHEN Jun-ling, YANG Rong-chang, MA Ren-le. Structural design optimization of a composite tower for large wind turbine systems[J]. Journal of Hunan University: Natural Sciences, 2015, 42(5): 29-35.(In Chinese) [13]柯世堂,曹九发,王珑,等.风力机塔架-叶片耦合模型风致响应时域分析[J]. 湖南大学学报:自然科学版, 2014, 41(4): 87-93. KE Shi-tang, CAO Jiu-fa, WANG Long,etal.Time-domain analysis of the wind-induced responses of the coupled model of wind turbine tower-blade coupled system[J]. Journal of Hunan University: Natural Sciences, 2014, 41(4): 87-93. (In Chinese) [14]GB 50051—2013 烟囱设计规范[S].北京:中国计划出版社, 2013:106-108. GB 50051—2013 Code for design of chimneys[S]. Beijing:China Planning Press, 2013:106-108. (In Chinese) [15]GB 50019—2003 钢结构设计规范[S].北京:中国计划出版社, 2003:45-46. GB 50019—2003 Code for design of steel structures[S]. Beijing: China Planning Press, 2003:45-46. (In Chinese) [16]AGBAYANI N A. A technical overview of ASCE/AWEA RP2011: Recommended practice for compliance of large land-based wind turbine support structures[C]//Proceedings of Structures Congress 2014. Reston, Virginia: ASCE, 2014: 1759-1770. [17]GB 50135—2006 高耸结构设计规范[S].北京:中国计划出版社,2007:74-86. GB 50135—2006 Code for design of high-rising structures standard[S]. Beijing: China Planning Press, 2007:74-86. (In Chinese) [18]GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010:64-72. GB 50010—2010 Code for design concrete structure[S]. Beijing: China Architecture & Building Press,2010:64-72. (In Chinese) [19]GRÜNBERG J, GÖHLMANN J. Concrete structures for wind turbines[M]. Hoboken, New Jersey: John Wiley & Sons, 2013:116-120. [20]GB 50009—2012 建筑结构荷载规范[S].北京:中国建筑工业出版社,2010:8-12. GB 50009—2012 Load code for the design of building structure[S]. Beijing: China Architecture & Building Press,2010:8-12. (In Chinese) [21]赵远东, 方正华. 带有权重函数学习因子的粒子群算法[J]. 计算机应用, 2013, 33(8): 2265-2268. ZHAO Yuan-dong, FANG Zheng-hua. Particle swarm optimization algorithm with weight function’s learning factor[J]. Journal of Computer Applications, 2013, 33(8): 2265-2268.(In Chinese) [22]刘峡壁. 人工智能导论: 方法与系统[M]. 北京:国防工业出版社, 2008:263-266. LIU Xia-bi. Introduction to artificial intelligence: approaches and systems[M]. Beijing: National Defense Industry Press, 2008:263-266.(In Chinese) Geometry Optimization on Prestressed Concrete and Steel Segments of Wind Turbine Towers XU Bin1,2†, LI Ze-yu1, CHEN Hong-bing1 (1. College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China; 2. Hunan Provincial Key Lab on Damage Diagnosis for Engineering Structures,Hunan Univ, Changsha, Hunan410082, China) A prestressed concrete-steel hybrid tower structure was proposed to replace a conventional 2 MW steel tubular wind turbine tower structure. The height and section size of the prestressed concrete-steel hybrid tower were optimized by an updated partial swarm optimization algorithm, where the cost was taken as the optimal objective function, and the constraint conditions including the strength, stability and the stiffness of the prestressed concrete and steel tubular segments, as well as the fatigue, natural frequency, and the maximum top deflection of the hybrid tower structure were considered, but the shape of the tower was kept unchanged. The optimization results show that the total construction cost of the prestressed concrete-steel hybrid wind turbine tower satisfying all of the constraint considerations is about 27 % less than that of the conventional steel tubular wind tower. hybrid wind turbine tower; structural optimization; particle swarm optimization(PSO); traditional steel tubular wind turbine tower 1674-2974(2016)07-0025-07 2015-11-19 国家自然科学基金资助项目(51478175),National Natural Science Foundation of China(51478175) 许斌(1972-),男,湖北孝感人,湖南大学教授,博士 †通讯联系人,E-mail:binxu@hun.edu.cn TU398.9;TM614 A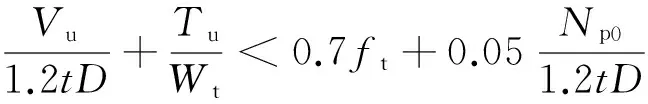
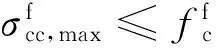

2 优化目标函数
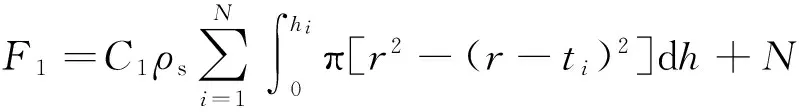

3 基于粒子群算法的组合塔架优化



4 优化分析算例

5 结 论

