含裂纹故障的转子-轴承系统的非线性特性分析*

张亚辉　赵　军

(91267部队　福州　350600)

ZHANG Yahui　ZHAO Jun

(No.91267 Troops of PLA, Fuzhou　350600)



含裂纹故障的转子-轴承系统的非线性特性分析*

张亚辉赵军

(91267部队福州350600)

针对含有初始弯曲转子系统在运行过程中出现的裂纹故障问题，建立了含有裂纹故障的转子分析模型，推导了其运动微分方程。采用数值方法分析研究裂纹深度、初始弯曲对系统振动的影响。结果表明：随着无量纲裂纹深度的增加，系统发生倒分岔现象提前；当考虑初始弯曲时，系统响应在临界转速附近的混沌区域比不考虑时增大，且随裂纹深度增大变化缓慢。并进一步研究分析了初始弯曲量对系统振动特性的影响。论文的研究工作能够更加真实地模拟出实际转子系统的响应特征，更好地为转子系统的安全稳定运动和故障的诊断提供理论参考。

裂纹; 转子系统; 非线性振动

ZHANG YahuiZHAO Jun

(No.91267 Troops of PLA, Fuzhou350600)

Class NumberTB561；U661.42

1　引言

转子是航空和船用汽轮机组的关键部件，其工作环境非常恶劣，长期处于高温介质中高速旋转，逐渐形成疲劳裂纹源进而扩展，裂纹会导致转轴刚度降低，从而引起转子横向振动幅值变大，形成运行故障进而影响机组正常工作，严重影响飞机和船舶在航率和安全性。引起转子异常振动或振动过大的原因有很多，转轴裂纹是主要原因之一[1]。

工程实际中，转子的弹性轴有时会存在一定的初始弯曲，即弹性轴在不受力的情形下其轴线并不是一条理想的直线。造成转子初始弯曲的原因各不相同，有制造安装误差的问题，也有运行中热效应等问题。转子的弹性轴出现弯曲后，必然引起相应的质量偏心，造成转子的动扰度增加，机组的振动加剧，甚至能引发转子与静子之间的碰摩[2]。

瓮雷，杨自春等[3～4]分析研究了气流激振力作用下转子系统的非线性振动特性。张韬、孟光[5]分析了具有初始弯曲和刚度不对称转子系统的碰摩响应，得到了参数对系统分叉和混沌响应的影响。林富生，孟光[6]以飞行器内等速运动的同时存在初始弯曲和横向裂纹的转子轴为研究对象，分析研究了飞行器机动飞行对转子系统振动响应的影响。

以上文献都是基于简单的模型分析初始弯曲对裂纹转子系统的动力学响应，而工程实际中转子系统非常复杂，为了更进一步研究初始弯曲对裂纹转子振动特性的影响，本文综合考虑了非线性油膜力以及裂纹交叉刚度，建立了含初始弯曲的转子-轴承系统。通过数值仿真，分析研究了初始弯曲和裂纹深度对系统的振动响应。

2　系统动力学方程

本文以含有裂纹故障的对称刚性油膜支承的转子-轴承系统作为研究对象，忽略扭转振动和陀螺力矩，只考虑转子的横向振动，如图1所示，研究在汽轮机非线性间隙气流激振力作用下的非线性动态响应。其中O1、O2分别为轴承内瓦和转子几何中心，O3为转子质心；转子两端由半径为R、长为L的滑动轴承支承，m1、c1和m2、c2分别为转子在轴承处和圆盘处的等效集中质量和结构阻尼，e为圆盘的质量偏心，Fx、Fy为非线性油膜力[7]。

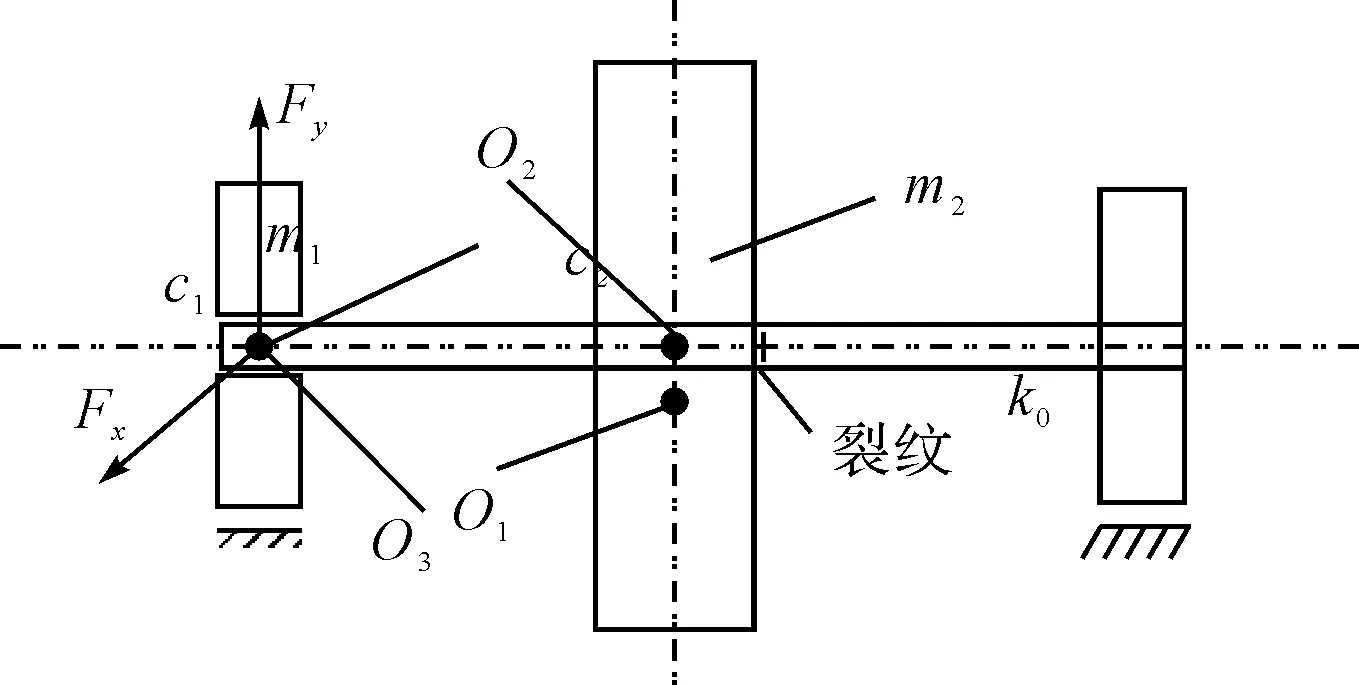
图1　油膜支承裂纹转子系统示意图

2.1裂纹刚度模型

转子轴在无裂纹时的刚度为k0,kxx为x方向的刚度；kxy、kyx为x,y方向交叉的刚度；裂纹在ξ方向和η方向的刚度变化量为kξ和kη；ω为转速；β为不平衡量与裂纹法向的夹角。转子系统的刚度矩阵无量纲形式可表示为[8]

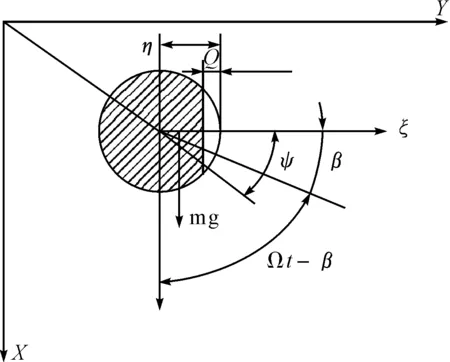
图2　转子裂纹轴横断面示意图

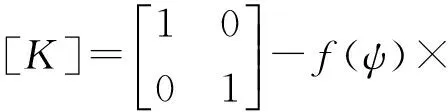
(1)

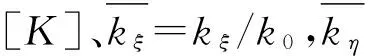
(2)

开闭函数当a/R<0.5时采用GASCH的铰链弹簧模型，a/R≥0.5时采用MAYES提出的裂纹模型[9]，开闭函数表达式如下：

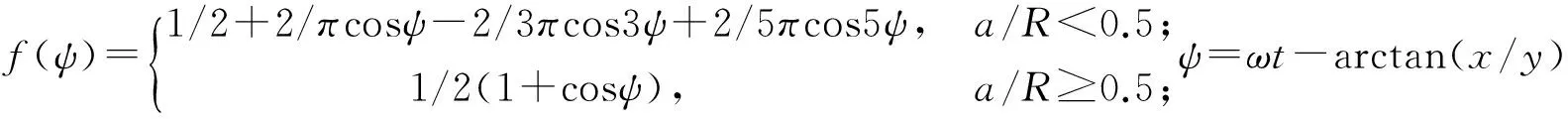
(3)

2.2转子运动微分方程

只考虑系统的横向振动，忽略扭转振动和陀螺力矩，则在非线性油膜力作用下考虑初始弯曲的含

裂纹转子系统运动微分方程的无量纲运动微分方程如下：

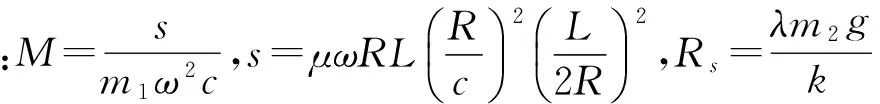
3　仿真结果与分析

鉴于本文运动微分方程具有强非线性特征，采用四阶龙格库塔方法研究分析参数变化时系统的各种动力学现象，获取不同参数变化下的振动响应，进而给出在非线性油膜力作用下含有初始弯曲的转子在裂纹故障时的振动分岔图、轴心轨迹和Poincare截面图。

本文转子轴承系统的主要参数为：m1=4.0kg，m2=32.1kg，R=25mm，L=12mm，μ=0.018pa·s，c1=1050N·s/m、c2=2100N·s/m、k=2.5×106N/m，b=0.11mm，气流激振力的参数选取如下：ρ0=11.8kg/m3，RT=0.5m，RB=0.37m，β1=35°，β2=40°，ζ=0.83，δ=1.2×10-3m，V=200m/s。系统一阶临界转速为ω0=882.5rad/s。

3.1裂纹深度对系统动力学特性的影响

裂纹深度对转子系统的非线性动力学响应产生不同的影响。如图3和图4所示，分别给出了初始弯曲量为λ=0.3时，在非线性油膜力作用下不考虑和考虑初始弯曲时不同裂纹深度下裂纹转子轴承系统的振动响应随转速ω变化的分岔图。图3为不考虑初始弯曲的裂纹转子系统的分岔图，与文献[10]中的分岔图类似，但文献采用的是余弦波模型，虽然考虑了裂纹之间的开闭的过度过程，但没能较好地反映裂纹的常开与常闭阶段，这与实际情况也是不相吻合的。

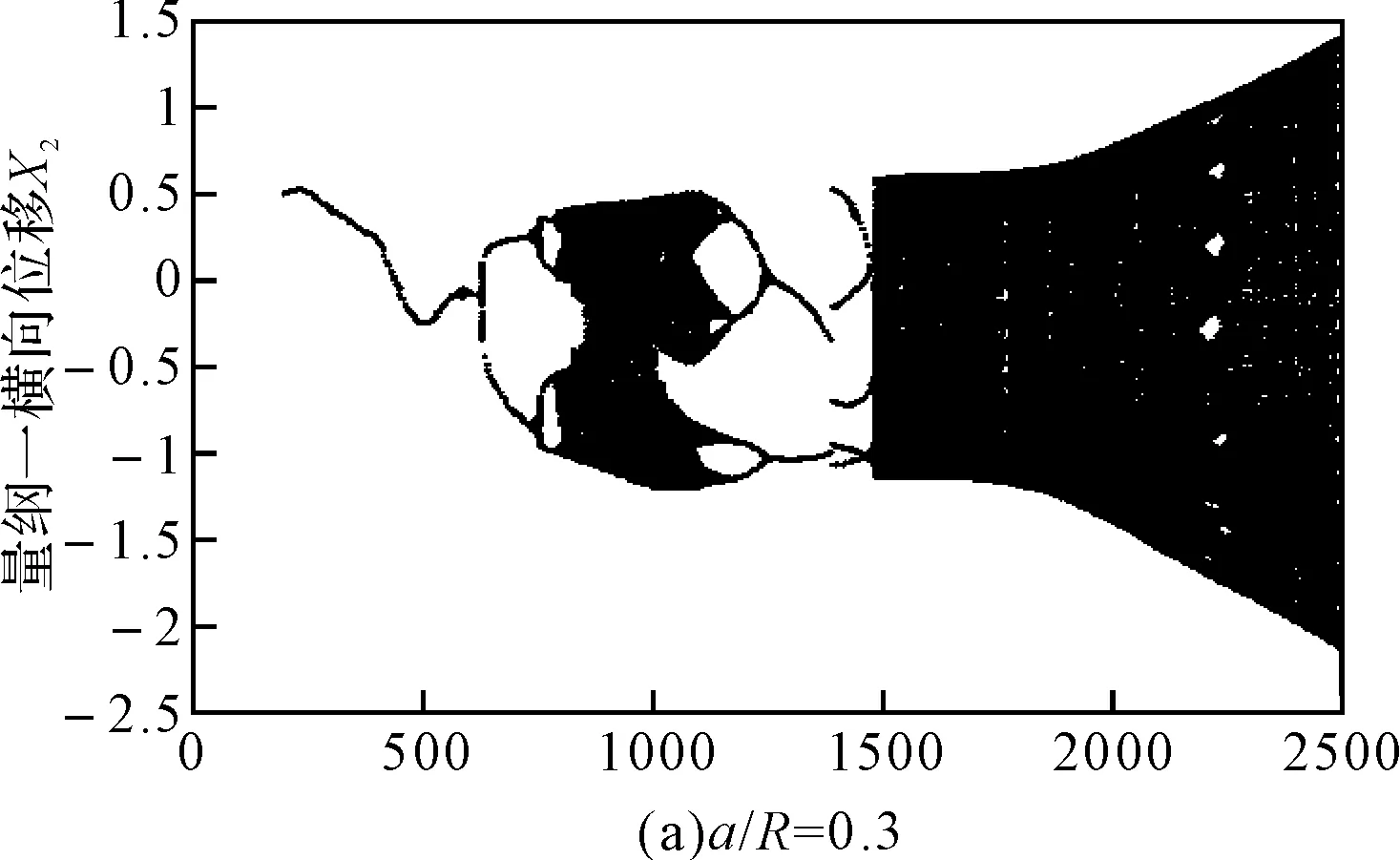
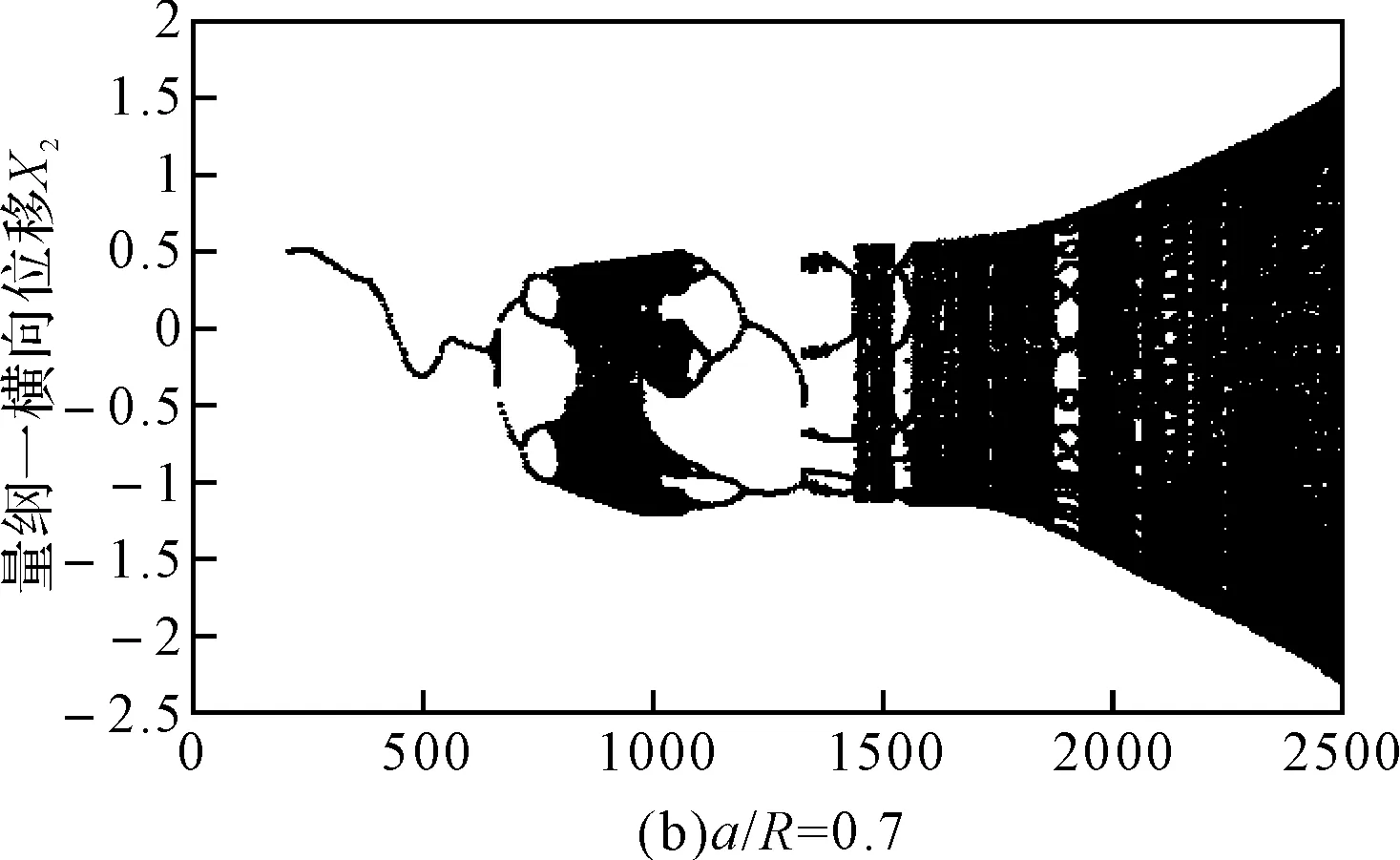
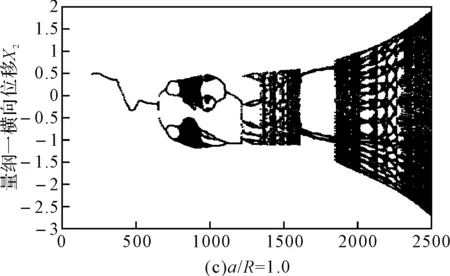
图3　无初始弯曲时不同裂纹深度系统随转速变化的分岔图

本文采用的模型可以综合考虑裂纹深度对裂纹轴刚度的影响，能够更加准确地说明含裂纹转子系统随裂纹深度变化的动力学响应。从图3可以看出，在转速比较低时，无量纲裂纹深度对转子系统的动力学响应影响较小，而对临界转速和超临界转速区域的动力学特性影响比较大。对比图3(a)、3(b)和3(c)可以看出，随着无量纲裂纹深度的增加，系统发生倒分岔现象提前，临界转速区域的混沌区域逐渐减小；由图3(b)和3(c)可以看出系统在超临界转速区域出现周期8和较长的周期3运动，且系统在临界转速区域的分岔图演变为两条自相似的轨迹。

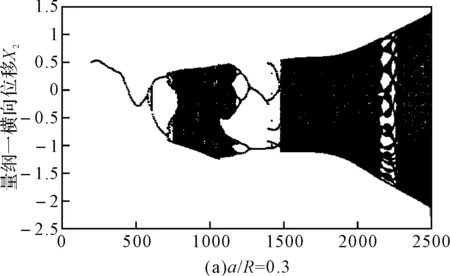
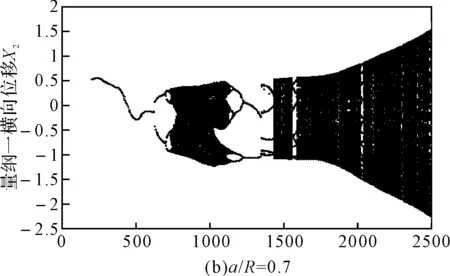
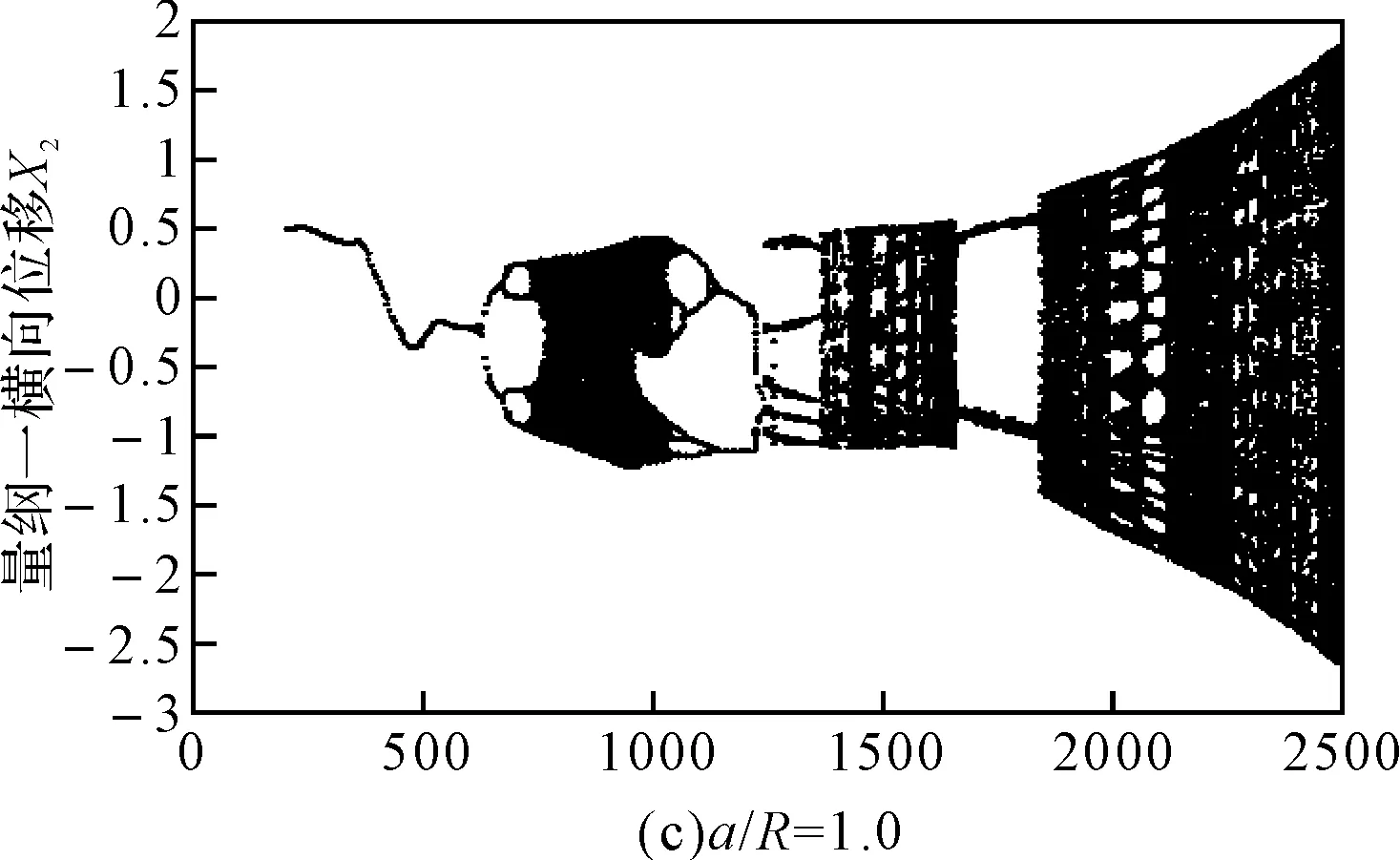
图4　含初始弯曲时不同裂纹深度系统随转速变化的分岔图

由图4可以看出，随着无量纲裂纹深度的增加，系统发生倒分岔现象提前，临界转速区域的混沌区域也逐渐减小，但相对无初始弯曲时变化不大；在超临界转速区域出现周期8和较长的周期2运动。对比图3和图4可以看出，转子系统随着无量纲裂纹深度的增加，在考虑初始弯曲时，转子系统响应在临界转速附近的混沌区域比不考虑初始弯曲时增大，随裂纹深度变化较无初始弯曲时变化缓慢，这主要是由于初始弯曲的存在使得系统的响应复杂化。因此，进一步研究初始弯曲对系统动力学响应的影响，是很有必要且十分有意义的。

3.2初始弯曲量对系统动力学特性的影响

为了进一步研究初始弯曲量对系统动力学特性的影响，以初始弯曲量λ作为控制参数，研究其变化对转子系统动力学行为的影响。图5给出了无量纲裂纹深度a/R=1.0、转速ω=1050rad/s时转子系统随初始弯曲量变化的响应分岔图。由图可以看出，随着初始弯曲量的增大，在油膜力和转子质量偏心作用下裂纹故障转子系统呈现出不同的非线性特征。

图5　无量纲裂纹深度a/R=1.0时振动响应随初始弯曲量变化图

在初始弯曲量较小时，系统呈现出周期4运动，如图6(a)所示，系统的轴心轨迹为4条交叉曲线，在Poincare截面上表现为4个离散的点。随着初始弯曲量的增大，转子的振动响应演变为周期8运动，如图6(b)所示，系统的轴心轨迹为8条交叉曲线，在Poincare截面上表现为8个离散的点。随着初始弯曲量的进一步增大，转子系统经过周期性分岔进入混沌运动，当λ=0.512时，系统出现短暂的周期12运动，如图6(c)所示，Poincare截面上为12个离散的单点，轴心轨迹为有限条曲线。之后又进入复杂的混沌运动。

图7给出了无量纲裂纹深度a/R=0.7、转速ω=1050rad/s时转子系统随初始弯曲量变化的响应分岔图，由图可以看出系统的响应在初始弯曲量λ=0.629附近出现短暂的周期12运动外，都处于混沌运动状态。图8为不同初始弯曲量下转子系统的轴心轨迹图和Poincare截面图。对比图5、6和图7、8可以看出：在无量纲裂纹深度较小时，系统的动力学响应主要受初始弯曲的影响，系统响应除了出现短暂的周期12运动外，基本上处于混沌运动状态；随着无量纲裂纹深度的增加，无量纲裂纹深度导致系统的动力学特性逐渐变得明显，在不同的初始弯曲量下系统的响应交替出现周期运动和混沌运动。

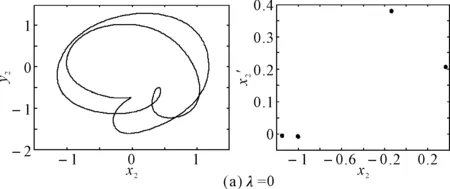
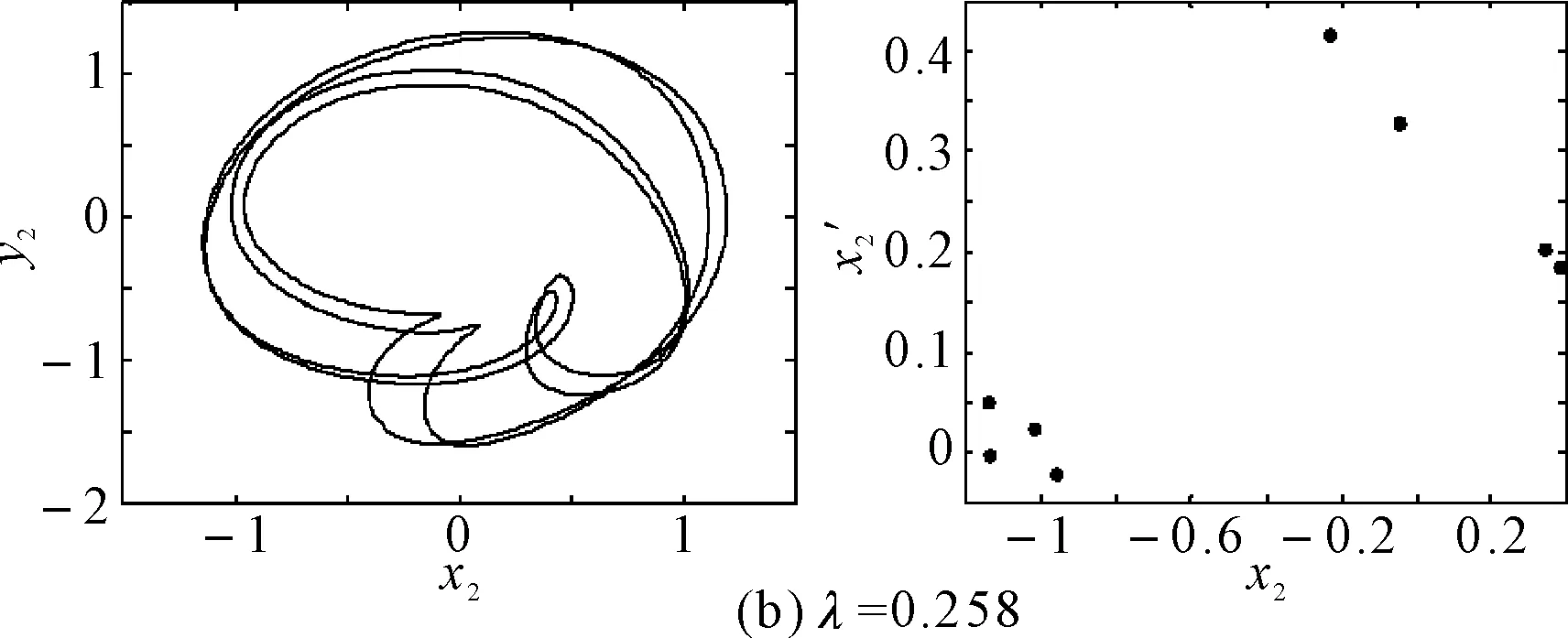
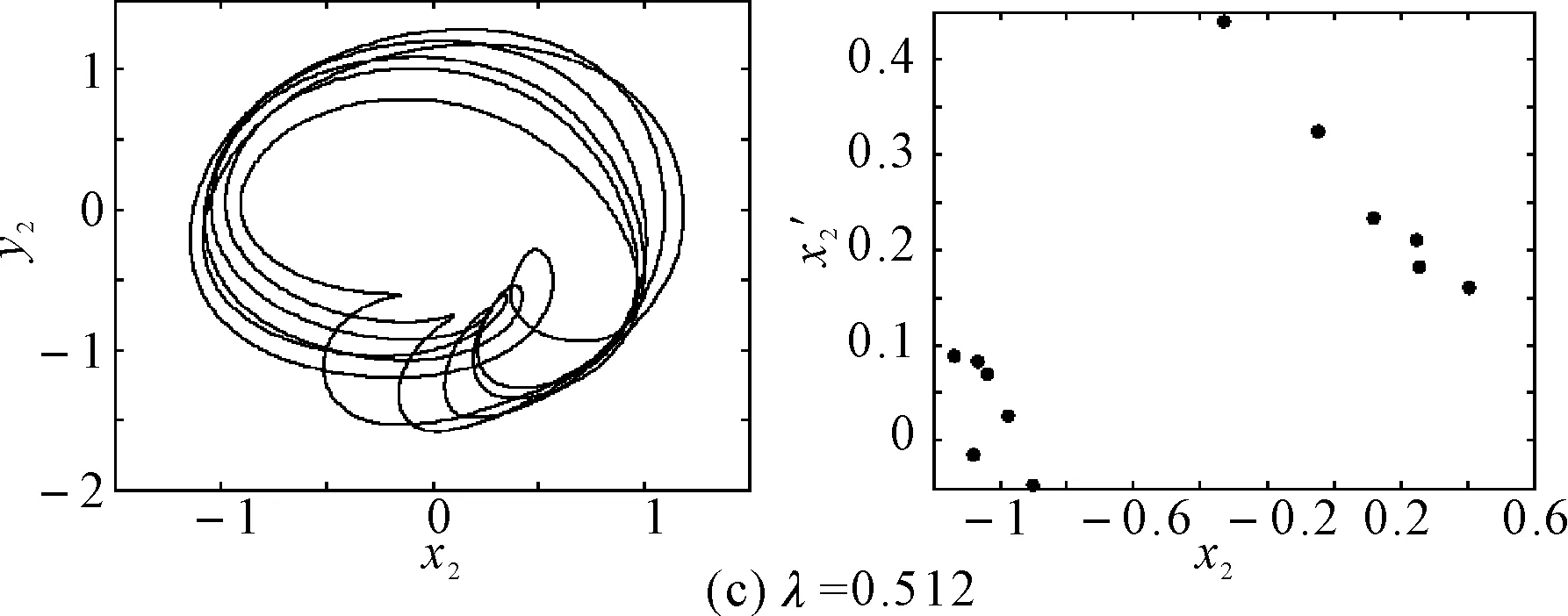
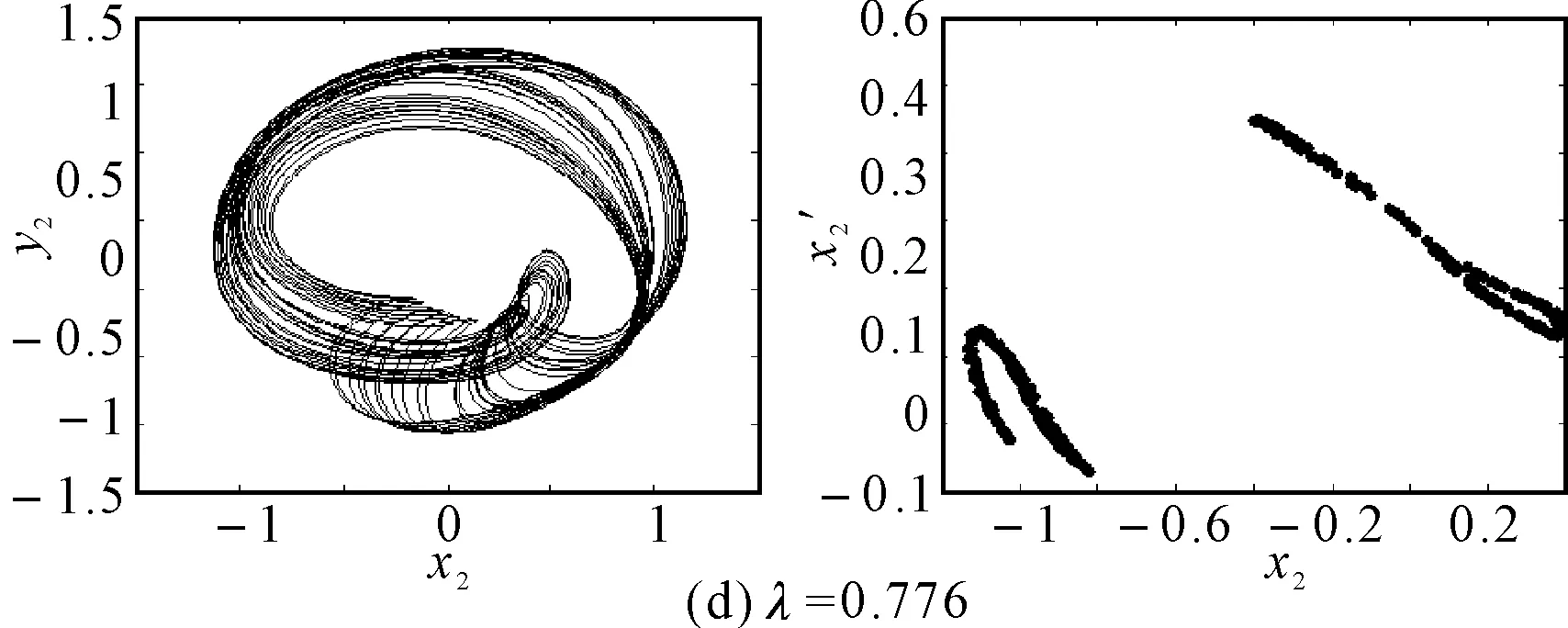
图6　裂纹深度a/R=1.0不同初始弯曲时转子轴心轨迹和Poincare截面图

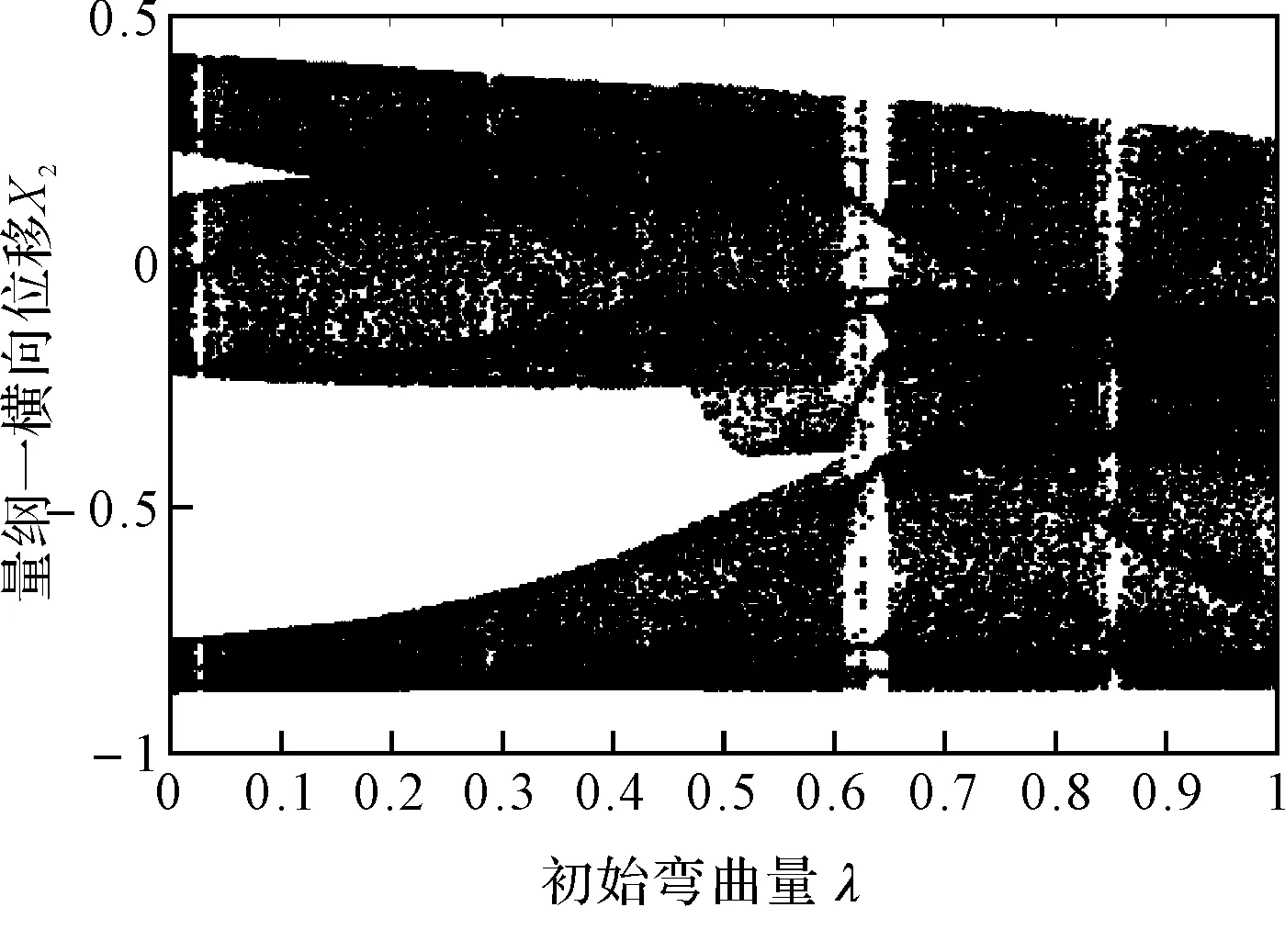
图7　无量纲裂纹深度a/R=0.7时振动响应随初始弯曲量变化图

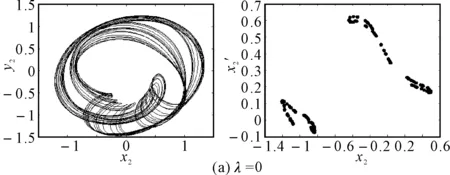
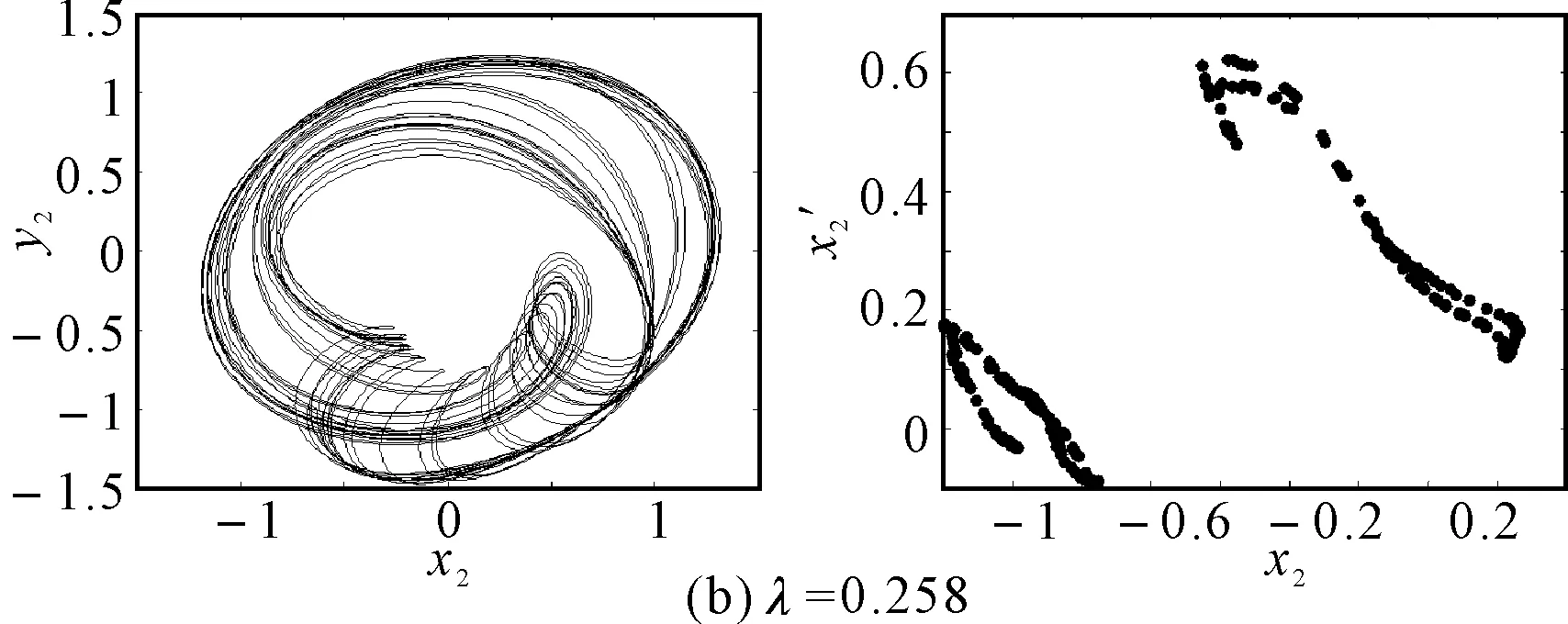
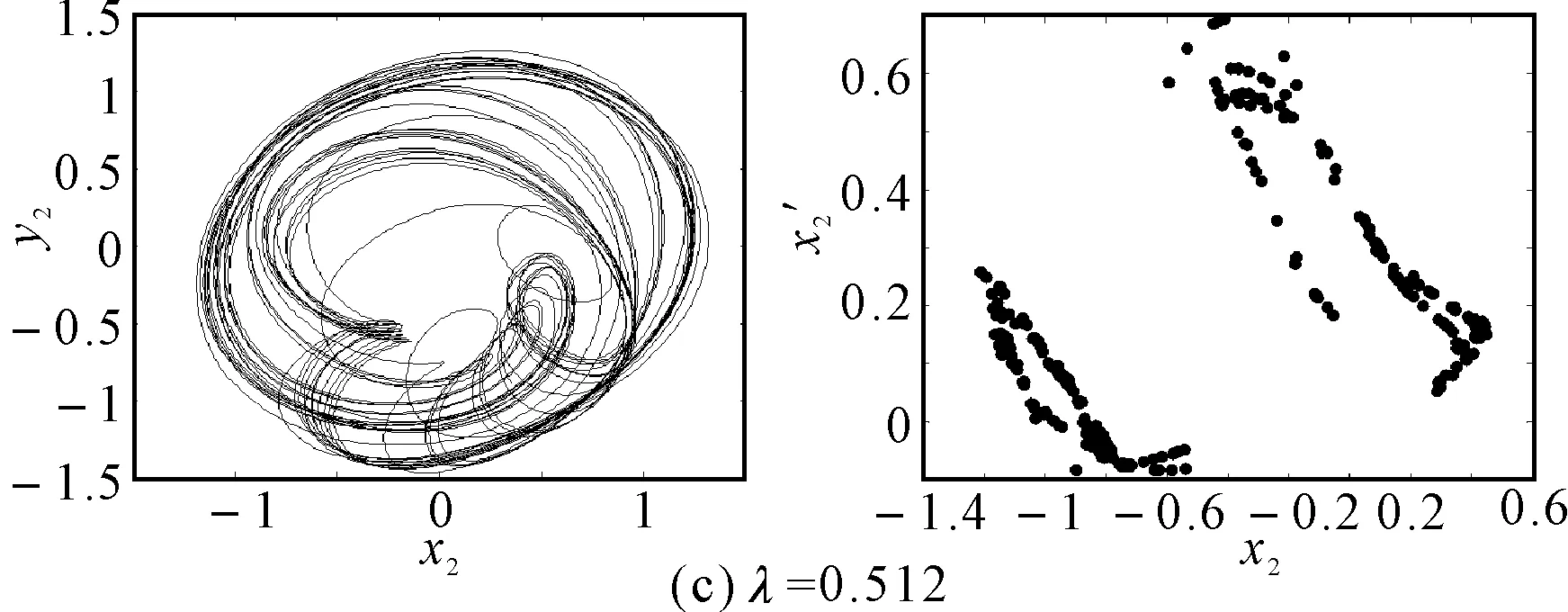
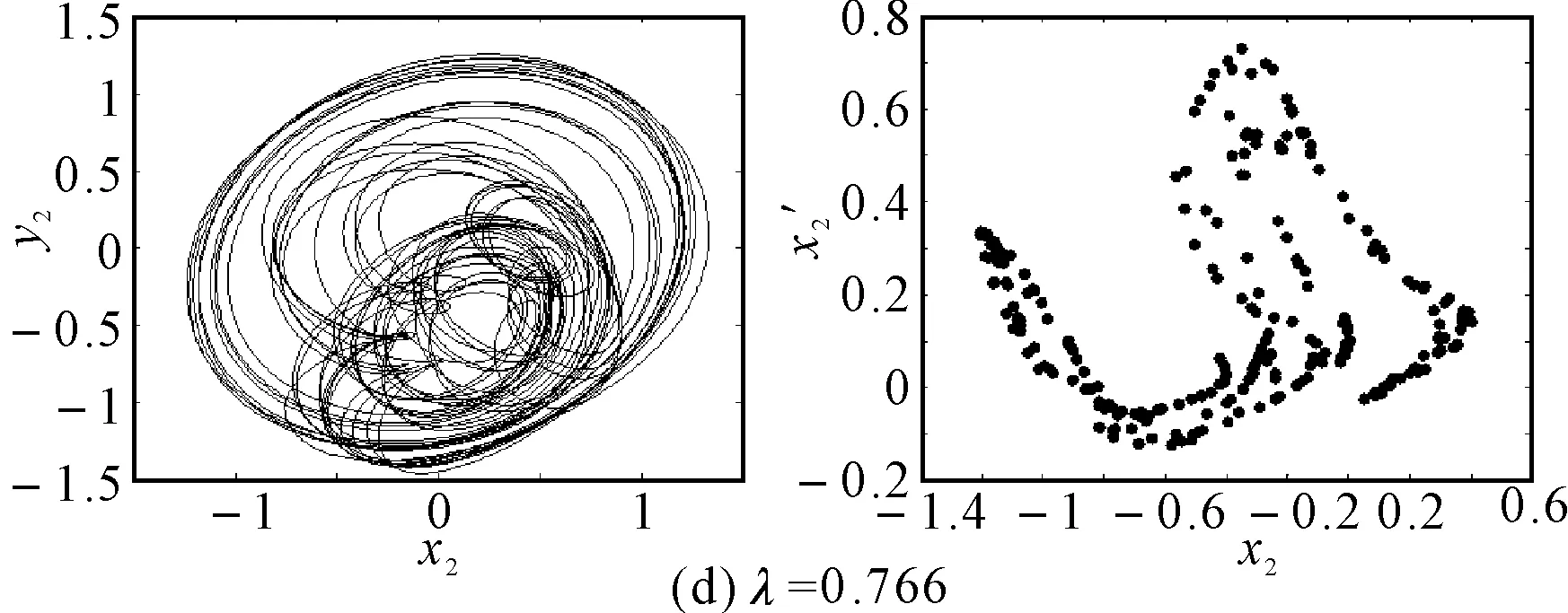
图8　裂纹深度a/R=1.0不同初始弯曲时转子轴心轨迹和Poincare截面图

4　结语

本文建立了在非线性油膜力和转子质量偏心作用下，考虑初始弯曲的含有裂纹故障的转子系统动力学分析模型，推到了系统的运动微分方程，通过数值仿真方法分析了在不同裂纹深度和初始弯曲量对系统非线性动力学特性的影响，得出如下结论：

1) 随着无量纲裂纹深度的增加，在转速较低时，无量纲裂纹深度对系统的动力学响应影响较小，而对转速在临界转速和超临界转速区域的动力学特性影响较大，且系统发生倒分岔现象提前；当考虑初始弯曲时，系统响应在临界转速附近的混沌区域比不考虑时增大，且随裂纹深度增大变化缓慢，这主要是由于初始弯曲的存在使得系统的响应复杂化。

2) 进一步研究分析了初始弯曲量对系统振动特性的影响，结果表明：在无量纲裂纹深度较小时，系统的动力学响应主要受初始弯曲的影响，系统响应除了出现短暂的周期12运动外，基本上处于混沌运动状态；随着无量纲裂纹深度的增加，无量纲裂纹深度导致系统的动力学特性逐渐变得明显，在不同的初始弯曲量下系统的响应交替出现周期运动和混沌运动。

本文考虑了转子系统在实际中存在的初始弯曲，能够更加真实地模拟出实际转子系统的响应特征，更好地为转子系统的安全稳定运动和故障的诊断提供理论参考。

[1] 赵常兴.汽轮机组技术手册[M].北京：中国电力出版社，2007.

[2] 黄文虎,夏送波.旋转机械非线性动力学设计基础理论与方法[M].北京：科学出版社，2006.

[3] 瓮雷,杨自春,曹跃云.汽轮机非线性间隙气流激振力作用下转子系统的分岔研究[J].海军工程大学学报，2015，27(5)：52-57.

[4] 瓮雷,杨自春,曹跃云.汽轮机非线性间隙气流激振力作用下含裂纹转子的振动特性研究[J].振动与冲击,2016,35(5):89-95.

[5] 张韬，孟光.具有初始弯曲和刚度不对称的转子碰摩现象分析[J].上海交通大学学报，2002，36(6)：844-848.

[6] 林富生，孟光.飞行器内含横向裂纹的初始弯曲转子的动力学特性研究[J].振动工程学报，2004，17(s)：16-18.

[7] 杨积东，徐培民，闻邦椿.裂纹转子分岔、混沌行为研究[J].固体力学学报，2002，23(1)：115-119.

[8] LI Ruqiang,LIU Yuanfeng. Simulation of crack diagnosis of rotor based on multi-scale singular-spectrum analysis[J].Chinese Journal of Mechanical Engineering,2006,19(2):282-285.

[9] 曾复，吴昭同，严拱标.裂纹转子的分岔与混沌特性分析[J].振动与冲击，2000，19(1)：40-42.

[10] 李振平，金志浩，徐培民，等.含横向裂纹的弹性转子-轴承系统的动力学研究[J].振动工程学报，2003，16(4)：468.471.

Nonlinear Characteristics of the Rotor-Bearing System with A Crack*

The dynamic model of a rotor system with crack fault is established. Considering the initial bend deformation of the rotor, and the movement differential equation is deduced. The effects of crack depth and the initial bending on the rotor system are analyzed using numerical methods. The results indicate that the phenomenon of the bifurcation happen in advance when the dimensionless depth of crack increase. And the response with initial bending is bigger than without initial bending, and the system response changes slowly with the depth of crack increase. And the effect of initial bending on the system is also analyzed in this paper. It indicates that the research on this paper can offer better theoretical reference for the fault diagnosis and safely running of rotor system.

crack, rotor system, nonlinear vibration

2016年2月13日,

2016年3月17日

张亚辉，男，工程师，研究方向：装备技术保障。赵军，男，硕士，助理工程师，研究方向：装备技术保障。

TB561；U661.42

10.3969/j.issn.1672-9730.2016.08.047