基于希尔伯特振动分解的低频振荡在线辨识

孟洁，李世明，温伯坚

(1. 三峡大学 电气与新能源学院，湖北 宜昌 443002；2. 广东电网有限责任公司电力调度控制中心，广东 广州 510600)



基于希尔伯特振动分解的低频振荡在线辨识

孟洁1，李世明2，温伯坚2

(1. 三峡大学 电气与新能源学院，湖北 宜昌 443002；2. 广东电网有限责任公司电力调度控制中心，广东 广州 510600)

利用希尔伯特振动分解(Hilbert vibration decomposition，HVD)算法适于处理时变频率信号的特性，提出一种处理非平稳振荡信号的新算法——结合HVD的信号能量分析法，并应用于电力系统低频振荡在线辨识中。首先，对通过Hilbert变换获得的解析信号进行分析和滤波，得到幅值最大分量的瞬时频率，并由同步检测获得相应的幅值和初相位；然后，通过迭代运算检测出非平稳振荡信号各分量的频率、幅值、相位；最后，运用信号能量法对通过HVD得到的各平稳信号的主导振荡模式进行识别和分离。将该算法与Prony算法、基于经验模态分解(empirical mode decomposition，EMD)的信号能量分析法进行比较，仿真测试和实例分析结果说明，此算法能够有效提取非轴对称振荡信号的主导模式，并且抗噪能力强、计算效率高。

低频振荡；非平稳信号；在线辨识；希尔伯特振动分解；信号能量分析法

随着电力系统互联规模的不断扩大和自动化设备的日益增多，低频振荡已成为系统运行安全的一大威胁。近年来，随着基于全球定位系统(global position system，GPS)的广域测量系统(wide area measurement system，WAMS)的不断推广[1]，技术人员可以获取海量的动态量测数据，而且数据精度不断提高，这为提取低频振荡特征提供了技术可能。

目前基于量测轨迹的低频振荡模式识别方法主要有快速傅里叶变换(fast Fourier transform，FFT)法、小波算法、Prony算法、希尔伯特-黄变换(Hilbert-Huang transform，HHT)法和信号能量分析法等[2-8]。FFT法通过频谱分析得到信号频率，但是无法分析信号的阻尼特性。小波算法在FFT的基础上，通过小波基函数给信号加窗，能有效反映信号的时频特性，但小波基函数不易确定。Prony算法通过指数函数的多阶线性组合来拟合采样信号，识别的信息量大、自适应能力较强，但其对噪声敏感，且准确性依赖于正确定阶[2]，此外传统的Prony算法无法处理非平稳振荡。HHT法可处理非平稳信号，但其经验模态分解(empirical mode decomposition，EMD)过程可靠性较差，难以避免虚假成分，使本征模态函数分量的物理意义不明确[3]。信号能量分析法[6-7]是近年来提出的一种根据发电机受扰轨迹分析系统动态特征的新算法，曾被用于估计电力系统的稳定传输极限和识别结构的机械阻尼比。文献[6]提出了一种分析主导振荡模式的信号能量法，但其能量分布源于经典二阶模型，要求被分析对象必须是包络线关于时间轴对称的振荡信号，因此经典的信号能量分析方法很难用于实际电力系统低频振荡参数的辨识。针对这一问题，文献[7]借助EMD方法可以将信号分解为经验模态函数这一特点，将高阶模式下的振荡信号进行EMD，得到若干轴对称分量，再利用能量权重判据筛选固有模态函数(intrinsic mode functions，IMF)，找到主导振荡模式分量，然后采用信号能量分析法辨识振荡频率和阻尼比。然而，EMD存在一个模式混淆的问题，众多研究成果表明其根本无法区分2个频率较为接近的振荡模式[9-10]。

本文将希尔伯特振动分解(Hilbert vibration decomposition，HVD)[11-13]和信号能量分析法相结合，提出一种更有效的振荡模式分离方法——结合HVD的信号能量分析法，该方法的显著优点是可以借助滤波将2个频率非常接近的振荡模式有效地进行分离。首先，对通过Hilbert变换获得的解析信号进行分析和滤波，得到非平稳频率成分中幅值最大分量的瞬时频率，并由同步检测获得相应的幅值和初相位；然后，通过迭代运算检测出非平稳振荡信号各分量的频率、幅值、相位；最后，运用信号能量法对通过以上HVD过程得到的各平稳信号的主导振荡模式进行识别和分离。

1　信号能量分析法原理

信号能量分析法基于能量耗散原理，可以将阻尼特性从半周期能量描述的物理过程中提取出来。设δ(t)为振荡信号，其中t为固定振荡时间点，则信号的能量E可定义为

式中t0为第一个过零点时间。

鉴于E的非负性，可定义半周期信号能量

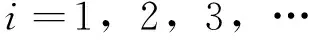
式中：ti为第i个过零点时间，Td为振荡周期。

对于经典二阶模型，则

式中：ωn为无阻尼固有频率，ξ为系统阻尼比。

又

若

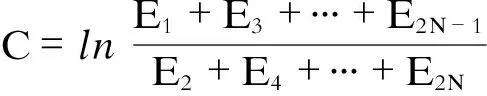
则振荡阻尼比

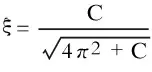
在已知振荡轨迹δ(t)的情况下，频率f可通过过零点检测求得。

该方法简单快捷、抗噪声干扰能力强，并且物理意义明确。但它的适用条件比较苛刻，要求分析对象满足其上、下包络线关于时间轴对称这一条件。文献[6]已证明，只有二阶模型的振荡信号能量分布才能满足这个条件。因此，经典的信号能量分析法很难用于实际电力系统低频振荡参数的辨识。

2　结合HVD的信号能量分析法

HVD是M.Feldman[11-12]等提出的一种非平稳信号处理方法，因最初应用于机械振动信号而得名。鉴于传统的信号能量法不能直接处理非平稳或非轴对称高阶模式信号，可借助HVD算法对信号进行平稳化预处理，然后再采用信号能量法进行分析。

2.1Hilbert变换

对于任一连续的时间信号x(t)，其Hilbert变换为

式中：y(t) 为经Hilbert变换后的时间信号，τ为时间。

x(t)与y(t)组成一复共轭对，得到解析信号

其中：

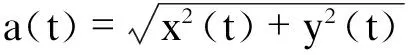
式中：a(t)为瞬时幅值，φ(t)为瞬时相位。

瞬时频率

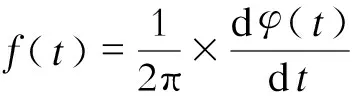
2.2幅值最大振荡分量的频率估计

考虑幅值和频率的非平稳性，振荡信号

式中：M为振荡模式的个数，al、fl、θl和φl分别为第l个振荡分量的幅值、频率、初相位和相位。

当M=2且振荡信号平稳时，由Hilbert变换获取x(t)的解析信号为

根据HVD原理，其瞬时幅值

其中

瞬时频率

(1)

式(1)表明：瞬时频率f(t)包含两个部分,即幅值最大(不妨设为a1)振荡分量的瞬时频率f1(t)及相对于f1(t)快速变化的不对称振荡高频分量。f1(t)可由f(t)的积分均值估计得到，也可采用平滑滤波或低通滤波法滤除f(t)中快速变化的频率成分后估计出来。

考虑振荡信号非平稳(瞬时幅值和瞬时频率时变)或者包含多个振荡模式(M≥3)时，瞬时幅值a(t)和瞬时频率f(t)的表达式更加复杂，但是在实际应用中采用低通滤波法同样可以提取出f1(t)[11]。

2.3幅值和相位估计

不失一般性，将以上估计得到的瞬时频率作为参考频率fγ，通过同步检测估计相应的瞬时幅值aγ和初相位θγ。将初始振荡信号分别与两参考正交信号相乘，得同相输出

(2)

正交相输出

(3)

通过低通滤波可滤除式(2)—(3)后半部分，得到如下表达式：

(4)

(5)

由式(4)—(5)可得：

2.4迭代运算

根据以上步骤提取当前幅值最大的振荡分量

从初始待检信号中减去当前检测出的幅值最大振荡分量xγ(t)，得到：

式中：r为迭代次数，Xr(t)为第r次迭代运算后去除检出振荡分量的信号残差值，X0(t)为原始振荡信号。以Xr(t)作为新的待检信号，为下一步迭代作准备，当残差值标准差小于0.001时停止迭代。

经HVD后得到的各振荡分量为平稳信号，满足经典信号能量法适用条件，于是可在此基础上采用信号能量分析法进行低频振荡参数辨识。

3　仿真测试及实例分析

3.1非平稳振荡信号分析

考虑包含2个振荡模式的待检信号，对结合HVD的信号能量分析法的低频振荡模式及参数辨识性能进行测试。测试信号

测试信号包含2个振荡模式，振荡频率分别为0.7 Hz和2.5 Hz，其波形如图1所示。由图1可见，测试信号为非平稳振荡信号。

图1　非平稳振荡测试信号波形

利用HVD对测试信号δ(t)进行分解，得2个振荡分量δ1和δ2，波形如图2所示。

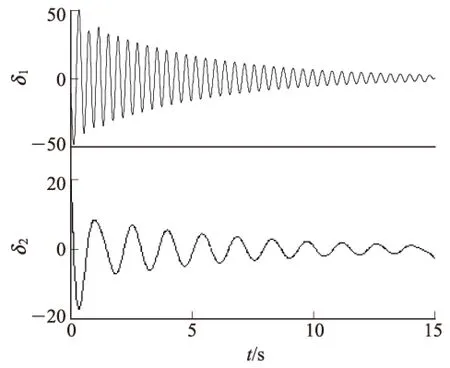
图2　非平稳振荡测试信号的HVD结果

对分解后的2个HVD分量分别进行信号能量分析，求相应的振荡频率，所得波形如图3所示。识别结果为：对于分量δ1，频率为2.491 8 Hz，阻尼比为0.012 3；对于分量δ2，频率为0.699 6 Hz，阻尼比为0.041 3。显然识别结果与原信号的真实值是一致的。

图3　非平稳振荡测试信号HVD分量的频率

由于HVD中Hilbert变换和低通滤波器对截断数据会产生边界效应，因此图3的两边界会出现频率不准确情况，在以后的研究中可以采用波形延拓法来避免这种边界效应，本文不作进一步研究。

为了进一步验证检测结果的有效性，分别对原信号进行Prony分析和基于EMD的信号能量分析，结果见表1。

表1非平稳振荡信号2种分析方法的识别结果对比

分析方法频率/Hzδ1δ2ξδ1δ2Prony算法2.50000.70000.01270.0341基于EMD的信号能量分析法2.50000.70040.01240.0338

Prony算法的分析结果和新方法的分析结果较一致，验证了结合HVD的信号能量分析法的有效性。基于EMD的信号能量分析法显然也可以将振荡频率分别为0.7 Hz和2.5 Hz的2个振荡模式分离，但是众多研究成果表明，如果2个模式的频率相差在1倍以内，EMD法无法有效地将之分离，而电力系统低频振荡模式之间很可能彼此频率较为接近，例如南方电网长期存在频率为0.4 Hz和0.6 Hz的振荡模式。

3.2频率非常接近的仿真信号分析

考虑包含频率非常接近的振荡模式的待检信号，对结合HVD的信号能量分析法的性能进行测试。取测试信号

测试信号含有2个振荡模式，振荡频率分别为2.5Hz和2.3Hz，测试信号的波形如图4所示。

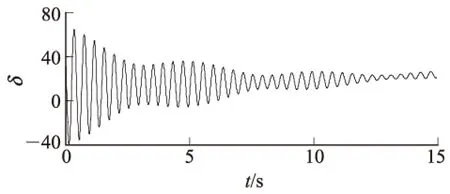
图4　频率非常接近的测试信号波形

对测试信号进行HVD，得到两个分量δ1和δ2，波形如图5所示。

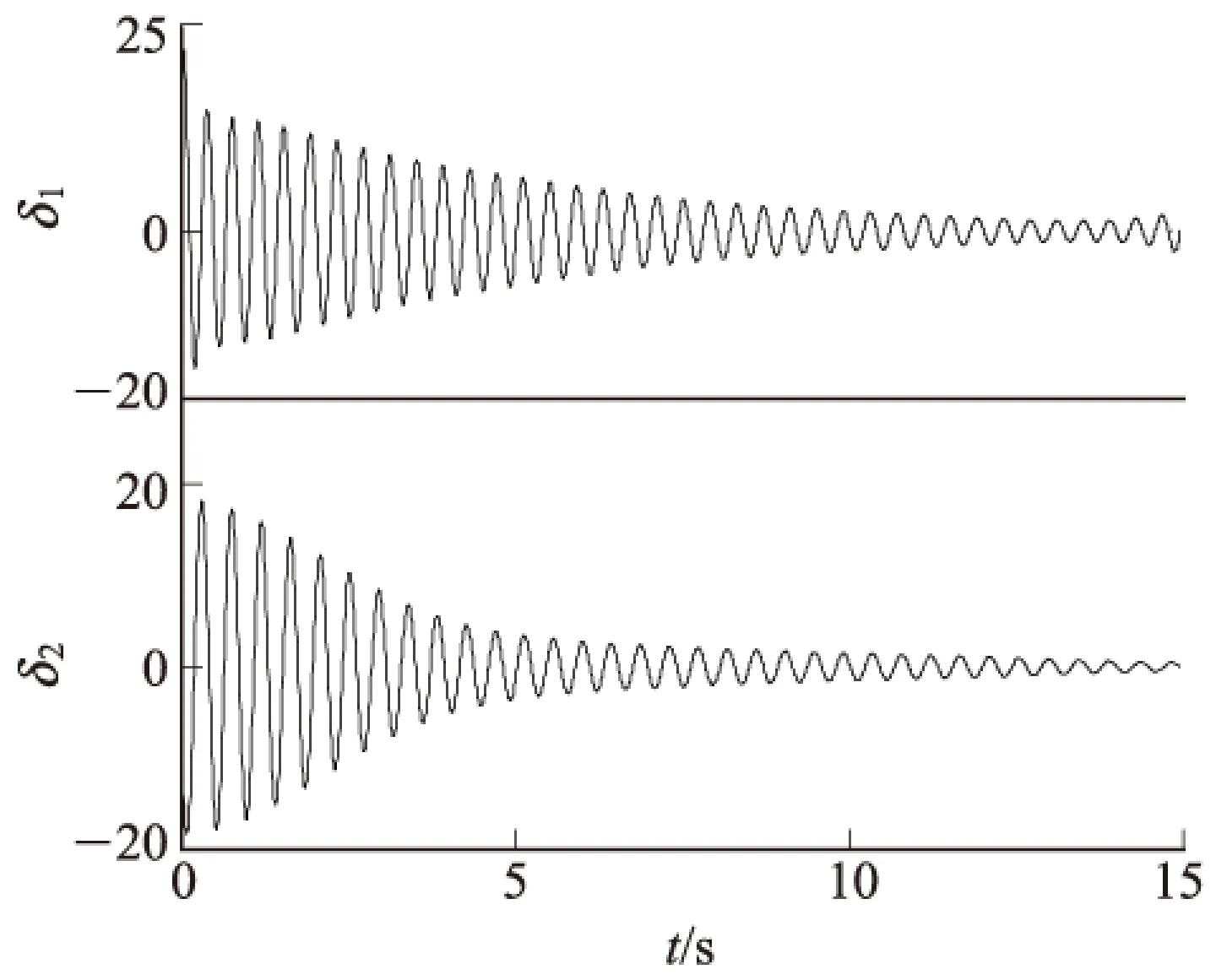
图5　频率非常接近的测试信号HVD结果

采用信号能量分析法验证δ1和δ2是否和原信号包含的2个振荡模式相吻合，结果见表2。

表2频率非常接近的测试信号2种分析方法识别结果

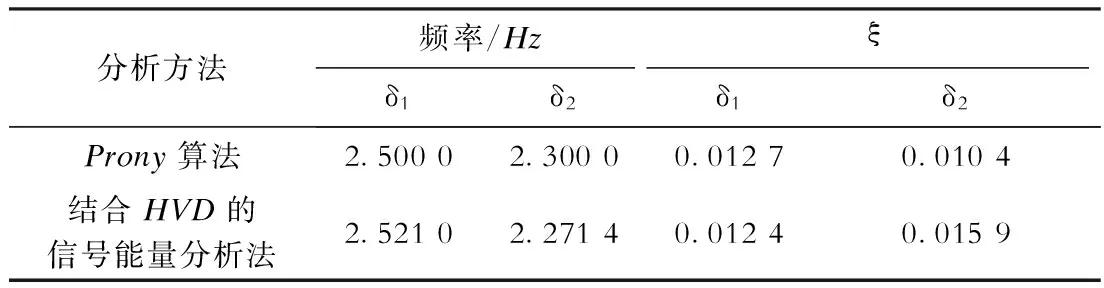
分析方法频率/Hzδ1δ2ξδ1δ2Prony算法2.50002.30000.01270.0104结合HVD的信号能量分析法2.52102.27140.01240.0159

由表2可看出：结合HVD的信号能量分析法的分析结果与真实值一致，而且与Prony算法的分析结果相差无几，从而验证了该方法是可以区分频率较为接近的振荡模式的。

3.3抗噪声性能分析

为了进一步验证结合HVD的信号能量分析法的抗噪声能力，在图1的非平稳振荡测试信号中加入10dB的白噪声信号。加入白噪声后的测试信号波形如图6所示。

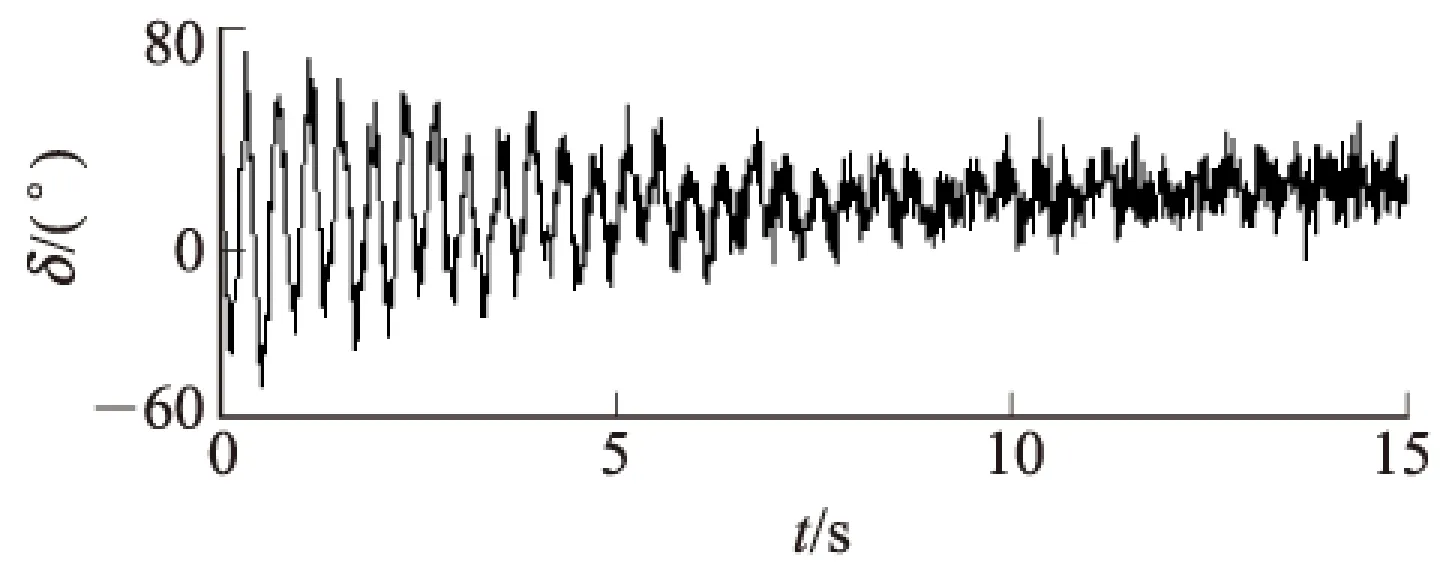
图6　含白噪声的测试信号波形

对加入白噪声的信号进行HVD，得到分量δ1和δ2，其波形如图7所示。识别结果为：对于分量δ1，频率为2.500 5Hz，阻尼比为0.012 8；对于分量δ2，频率为0.676 0Hz，阻尼比为0.055 3。

图7　含白噪声的测试信号HVD分解结果

对比3.1节的分析结果，新方法分析结果与真实情况和Prony算法的识别结果基本一致，但Prony算法计算时间特别长，而本文提出的算法通过HVD对非平稳信号轴对称化处理，能筛选出低频振荡主导分量，过滤了高频非主要成分，计算时间明显较短。

3.4实例分析

为了更好地说明结合HVD的信号能量分析法的实用性，以中国某省级电网实际低频振荡的相量测量单元(phasormeasurementunit，PMU)监测数据为测试信号进行仿真分析。

3.4.1案例1

2013年南方电网某中调WAMS监测到某电厂一机组发生功率波动(如图8所示)，并发出低频振荡预警信号，波动持续约51s，振荡频率为0.11Hz，阻尼比为-0.008。采样时间间隔为0.01s，采样点数为12 000。

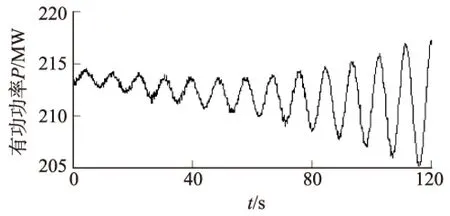
图8　振荡机组的有功功率实测数据

图9　振荡机组有功功率实测信号的HVD分解结果

通过HVD对该功率波动曲线进行分解，结果如图9所示。由图9可看出：δ1是这次振荡事件中唯一的主导振荡模式；平稳化后信号的上下包络线关于时间轴对称，符合信号能量分析法的适用条件。以15s为数据窗宽，对δ1进行信号能量分析，得到2个不同时段的主导振荡模式，结果见表3所示。

表3案例1结合HVD的信号能量分析法分析结果

分析时段/s振荡模式频率/Hz阻尼比20～3540～45δ1δ20.11150.1137-0.0112-0.0107

由表3可知，通过HVD和信号能量分析得到的主导振荡模式与已知的真实情况是一致的。为了进一步验证该方法的优越性，对此振荡信号采用基于EMD的信号能量分析法进行处理，结果见表4。

表4案例1基于EMD的信号能量分析法分析结果

分析时段/s振荡模式频率/Hz阻尼比20～3540～45δ1δ20.10390.1211-0.0302-0.0411

由表4可见，基于EMD的信号能量分析法虽然也可以近似辨识出振荡模式的频率，但是计算出的阻尼比误差较大。

3.4.2案例2

2011年南方电网某中调WAMS监测到低频振荡告警事件，振荡频率大约为0.6Hz，振幅最大的线路A的波形如图10所示，振荡幅值达109MW，振荡持续时间约6min，其中前2min振荡幅度较大。采样时间间隔为0.02s，采样点数为6 000。

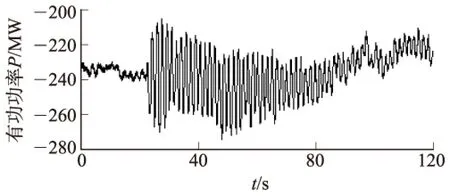
图10　振荡线路A有功功率实测数据

应用Prony算法对此次低频振荡事件进行分析，以15s为窗宽，得到3个不同时段的主导振荡模式，具体数据见表5。

表5案例2 Prony算法的分析结果

分析时段/s模式频率/Hz阻尼比24～39模式10.61680.0048模式20.51440.5144模式30.3521-0.111044～59模式10.61320.0060模式20.49150.0398模式3——64～79模式10.61590.0100模式20.50680.0403模式30.32280.0567

由表5可知，该次振荡事件的主导振荡模式有3个，分别位于0.6Hz、0.5Hz和0.3Hz附近，其中频率为0.3Hz的振荡模式幅值极小，且在44～59s时间段内近乎不存在。为了分析基于EMD的信号能量分析法能否区分这3个频率较为接近的振荡模式，对图10的功率曲线进行EMD，结果如图11所示，其中PIMFi为通过EMD得到的振荡分量i的有功功率，i=1,2,…,5。

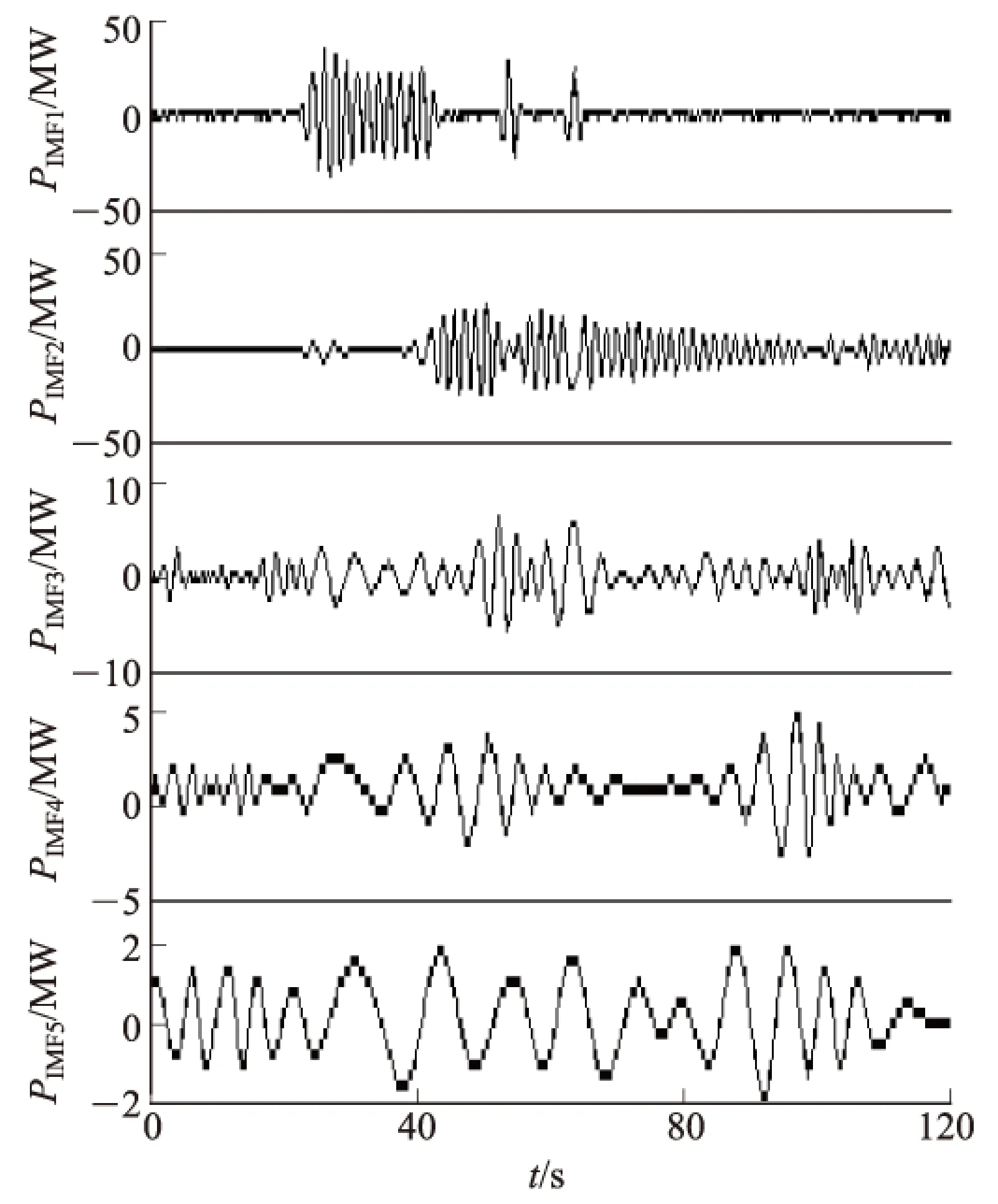
图11　振荡线路A功率曲线的EMD结果

应用信号能量分析法对得到的分解结果进行分析，得到不同时段的主导振荡模式，具体数据见表6。

表6　案例2基于EMD的信号能量分析法分析结果

由表6可见：基于EMD的信号能量分析法在3个时段都没有辨识出位于0.5Hz附近的振荡模式，且辨识出的位于0.3Hz附近的振荡模式也出现了极大误差，说明基于EMD的信号能量分析法在区分频率较为接近的振荡模式是很困难的。

为验证本文方法的有效性，采用结合HVD的信号能量分析法对图10的功率曲线进行分析，图12为HVD结果，其中x为对原功率曲线进行平稳去噪处理后的信号，x1、x2分别为HVD得到的振荡分量，图13为利用信号能量分析法求得的频率分布情况。

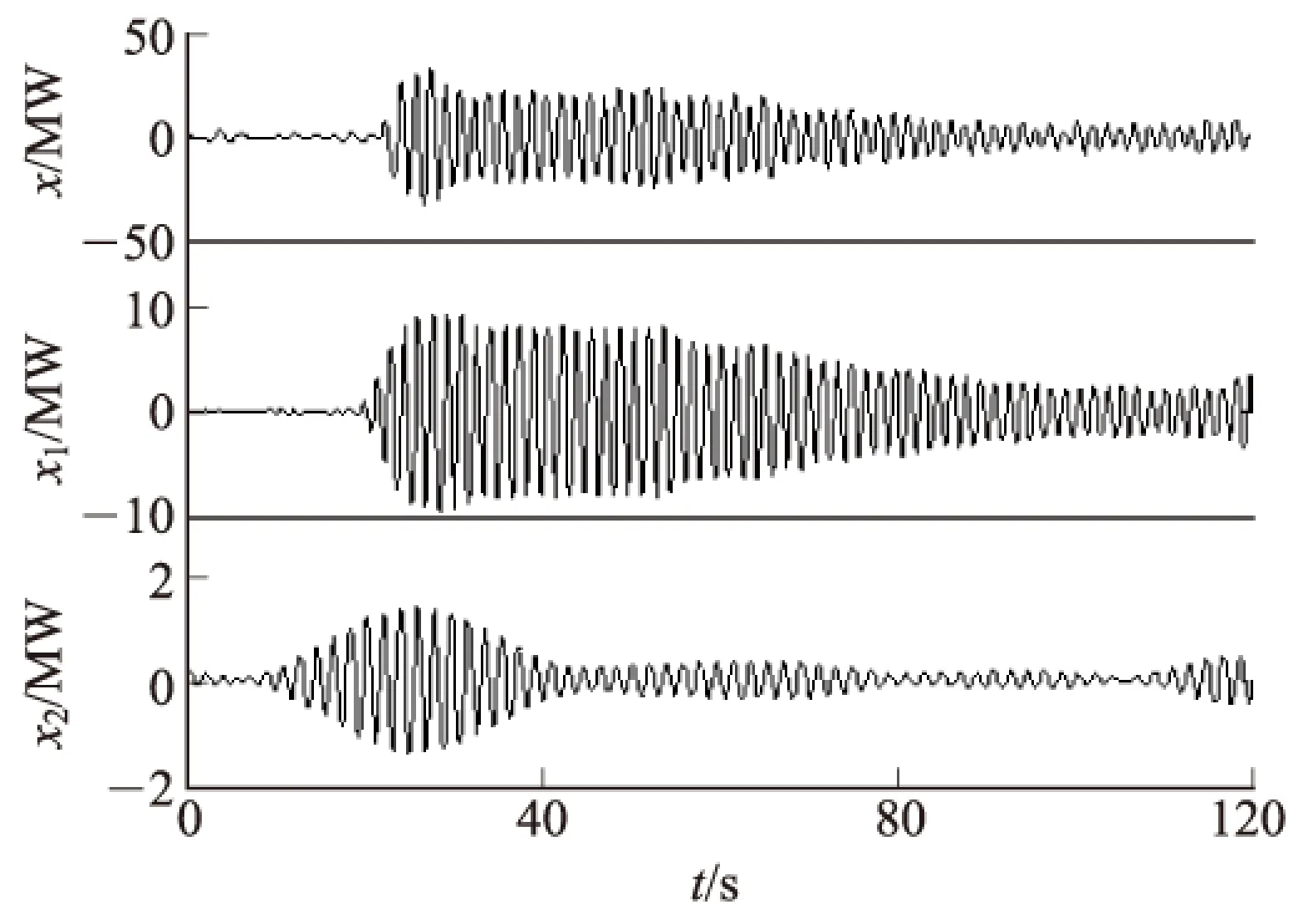
图12　振荡线路A功率曲线的HVD结果

图13　振荡线路A功率曲线HVD分量对应的频率

由图13可知：在不考虑HVD过程带来的边界效应的情况下，应用结合HVD的信号能量法得到的结果与Prony算法的分析结论是一致的，能准确辨识出频率较为接近的两振荡模式，其中f1=0.615 3Hz，对应的阻尼比ξ1=0.002 1，f2=0.513 5Hz，对应的阻尼比ξ2=0.064 9。

由于结合HVD的信号能量分析法在处理非平稳振荡信号方面具有优势，且可以区分频率较为接近的复合振荡模式，因此可以将Prony算法和结合HVD的信号能量分析法结合起来，研究南方电网中平稳振荡和非平稳振荡问题。

4　结论

a)本文提出结合HVD的信号能量分析法，将HVD引入电力系统低频振荡的非平稳振荡信号处理中，不仅拓展了传统信号能量分析法的适用范围，还提高了算法的抗噪能力。

b)本文提出的方法以HVD为核心，通过Hilbert变换和低通滤波器实现，不需要其他复杂的信号处理技术，与基于EMD的信号能量法相比不需要复杂的EMD过程，大大提高了计算效率。

c)基于EMD的信号能量分析法无法区分南方电网中长期存在的频率较为接近的振荡模式，而本文提出的结合HVD的信号能量分析法却能够很好地解决这一问题，有良好的应用前景。

[1]许树楷，谢小荣，辛耀中.基于同步相量测量技术的广域测量系统应用现状及发展前景[J]. 电网技术，2005，29(2)：44-49.

XUShukai，XIEXiaorong，XINYaozhong.PresentApplicationSituationandDevelopmentTendencyofSynchronousPhasorMeasurementTechnologyBasedWideAreaMeasurementSystem[J].PowerSystemTechnology，2005，29(2)：44-49.

[2]黄冉，李晓明.基于WAMS的低频振荡模式分析法的研究综述[C]//《电力系统保护与控制》杂志社，华北电力大学电气与电子工程学院. 中国电力系统保护与控制学术研讨会论文集. 许昌：《电力系统保护与控制》杂志社，2008：604-608.

[3]李天云，谢家安，张方彦，等.HHT在电力系统低频振荡模态参数提取中的应用[J]. 中国电机工程学报，2007，27(28)：79-83.

LITianyun，XIEJiaan，ZHANGFangyan,etal.ApplicationofHHTforExtractingModelParametersofLowFrequencyOscillationsinPowerSystems[J].ProceedingsoftheCSEE，2007，27(28)：79-83.

[4]罗骏，周崇雯，汪芳宗，等.基于不完全S变换的低频振荡在线辨识方法[J]. 广东电力，2015，28(7)：62-67.

LUOJun，ZHOUChongwen，WANGFangzong，etal.OnlineIdentificationMethodforLowFrequencyOscillationBasedonIncompleteSTransform[J].GuangdongElectricPower，2015，28(7)：62-67.

[5]易建波，黄琦，丁理杰，等.提升经验模态分解检测低频振荡模式精度的改进算法研究[J]. 电力系统保护与控制，2013，41(22)：71-78.

YIJianbo，HUANGQi，DINGLijie，etal.ResearchonanImprovedAlgorithmtoEnhancetheDetectionAccuracyofLow-frequencyOscillationModesbyEmpiricalModeDecomposition[J].PowerSystemProtectionandControl，2013，41(22)：71-78.

[6]穆钢，王宇庭，安军，等.根据受扰轨迹识别电力系统主要振荡模式的信号能量法[J]. 中国电机工程学报，2007，27(19)：7-11.

MUGang，WANGYuting,ANJun,etal.SignalEnergyMethodforIdentificationofMainOscillationModeinPowerSystemBasedonDisturbedTrajectory[J].ProceedingsoftheCSEE，2007，27(19)：7-11.

[7]穆钢，史坤鹏，安军，等.结合经验模态分解的信号能量法及其在低频振荡研究中的应用[J]. 中国电机工程学报，2008，28(19)：36-41.

MUGang，SHIKunpeng，ANJun，etal.SignalEnergyMethodBasedonEMDandItsApplicationforResearchofLowFrequencyOscillation[J].ProceedingoftheCSEE，2008，28(19)：36-41.

[8]王娜娜，刘涤尘，廖清芬，等.基于EMD-TEO及信号能量分析法的主导低频振荡模式识别[J]. 电工技术学报，2012，27(6)：198-204.

WANGNana，LIUDichen，LIAOQingfen，etal.IdentificationoftheDominantInertialModeBasedonEMD-TEOandSignalEnergyMethod[J].TransactionsofChinaElectrotechnicalSociety，2012，27(6)：198-204.

[9]RILLINGG,FLANDRINP.OneorTwoFrequencies?TheEmpiricalModeDecompositionAnswers[J].IEEETransactionsonSignalProcessing, 2008, 56(1)：85-95.

[10]FELDMANM.AnalyticalBasicsoftheEMD:TwoHarmonicsDecompositionMechSystSignalProcess[J].MechanicalSystems&SignalProcessing, 2009, 23(7)：2059-2071.

[11]FELDMANM.Time-varyingVibrationDecompositionandAnalysisBasedontheHilbertTransform[J].JournalofSound&Vibration, 2006, 295(3/5)：518-530.

[12]FELDMANM.TheoreticalAnalysisandComparisonoftheHilbertTransformDecompositionMethods[J].MechanicalSystems&SignalProcessing, 2008, 22(3)：509-519.

[13]刘慧，刘国海，沈跃.采用希尔伯特振动分解的非整数次谐波检测新方法[J]. 高电压技术，2009，35(7)：1758-1764.

LIUHui，LIUGuohai，SHENYue.NovelMethodforNon-integerHarmonicsMeasurementUsingHilbertVibrationDecomposition[J].HighVoltageEngineering，2009，35(7)：1758-1764.

(编辑李丽娟)

Online Identification for Low Frequency Oscillation Based on Hilbert Vibration Decomposition

MENG Jie1, LI Shiming2, WEN Bojian2

(1.School of Electrical Engineering and New Energy, China Three Gorges University, Yichang, Hubei 443002, China; 2. Electric Power Dispatching Control Center of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510600, China)

On the basis of characteristic of Hilbert vibration decomposition (HVD) algorithm being suitable to deal with time-varying frequency signals, this paper proposes a kind of new algorithm combining with HVD for dealing with non-stationary oscillation signals named signal energy analysis method which is applied in online identification for low frequency oscillation of the power system. Firstly, it analyzes and filters analytic signals obtained from Hilbert conversion to get instantaneous frequency with the maximum component of amplitude as well as get relevant amplitude and initial phase by means of synchronous detection. Then, by iterative operation, it is able to detect out frequency, amplitude and phase of each component of non-stationary oscillation signals. Finally, the signal energy analysis method is used for identification and decomposition for the dominant oscillation mode of each stationary signal from HVD. This algorithm is compared with Prony algorithm and signal energy algorithm based on empirical mode decomposition (EMD), and results of simulating test and example analysis indicate that this new algorithm is able to effectively extract the dominant mode of off-axis-symmetrical oscillation signals which has strong noise proof ability and high computation efficiency.

low frequency oscillation; non-stationary signal; online identification; Hilbert vibration decomposition(HVD); signal energy analysis method

2015-12-30

2016-04-19

10.3969/j.issn.1007-290X.2016.08.014

TM71

A

1007-290X(2016)08-0071-08

孟洁(1990)，女，河南邓州人。在读硕士研究生，研究方向为电力系统运行与控制。

李世明(1984)，男，四川隆昌人。工程师，工学硕士，主要从事电网调度自动化系统的研究工作。

温伯坚(1963)，男，湖北武汉人。教授级高级工程师，工学硕士，主要从事电力系统分析及调度自动化方面的研究工作。