基于多状态信息修正优化组合的电力设备故障率计算方法

吴杰康, 胥志强, 徐庆焯, 鲍雨徽

(广东工业大学 自动化学院，广东 广州510006)



基于多状态信息修正优化组合的电力设备故障率计算方法

吴杰康, 胥志强, 徐庆焯, 鲍雨徽

(广东工业大学 自动化学院，广东 广州510006)

采用多状态修正优化组合预测方法，建立天气因素、材料绝缘老化和设备检修影响的3种状态修正优化组合预测电力设备故障率模型。针对各随机影响因素的特点，依据可拓性原理预测3种天气状态模型的故障率，由3种参数威布尔分布-Copula函数的联合失效概率密度法计算绝缘老化引起的设备故障率，基于Holt-Winters模型来预估设备检修造成的故障率，再采用果蝇算法加权组合优化所求得的各子模型的故障率，算出具有高准确度的预测值。以某地区的电力系统为实例进行分析，所得结果表明所述模型可有效提高设备故障率的预测精度，同时也验证了果蝇优化算法在求解多状态修正优化组合预测问题时的有效性。

电力设备；故障率；多状态信息；修正优化组合；果蝇优化算法

电力设备的可靠性运行保障了人们生活及社会生产，故其失效预测也愈显重要，组合预测法[1]、灰色预测法[2]和人工智能算法[3]等优化方法已广泛应用于求解设备失效率。大量研究表明：气象因素、材料绝缘老化等易对设备可靠性评估结果造成较大偏差[4-5]；Holt-Winter预测设备失效率的模型具有鲁棒性强、精度高的特性[6]；引入Copula函数可较准确分析电力系统的多维联合失效概率密度[7]；用关联函数定量化计算出受气象因素影响的设备发生某种故障的程度及其变化[8]。实践证明，采用组合预测模型预估设备失效率，克服了单一预测模型误差大、精度低等缺点[9]。常规组合预测法也有若干不足之处：某些预测方法并不适用于预测所有影响因素引起的故障率，降低了预测结果的可靠度；常规组合预测法难于满足大电网的发展需求，对设备故障的预测易产生错误性指导。基于此，本文提出相应的修正优化措施，分析大电网中影响设备运行的随机因素及可能引起的故障，确定各相应故障率的最佳预测方法，组合成修正优化组合预测方案，保证预测值的准确度，提高供电可靠性。

1　多状态信息修正优化组合方法

1.1修正优化组合预测原理

组合预测的核心思想就是对同一目标运用多种方法进行预测，再选取适当的权重对预测结果进行加权组合的一种预测方法[1]。本文所提出的多状态信息修正优化组合预测模型的基本原理如下：

(1)

若其子模型的拟合残差为

uti=xti-x′ti(t=1,2,…,n;i=1,2,…,m).(2)

则各子模型构成的拟合残差矩阵

(3)

本文借助最小二乘原理求解该模型的最优权重，其目标函数和约束条件为

(4)

令R=[1,1,…,1]，则有

(5)

用拉格朗日乘子法求解上式，得

(6)

则最优权重向量

(7)

目标函数的最小值

(8)

本文所建电力设备故障率修正优化组合预测模型正是基于天气因素、材料绝缘老化和设备检修三者综合因素的基础上建立的，其3种状态信息修正优化组合预测步骤如图1所示。

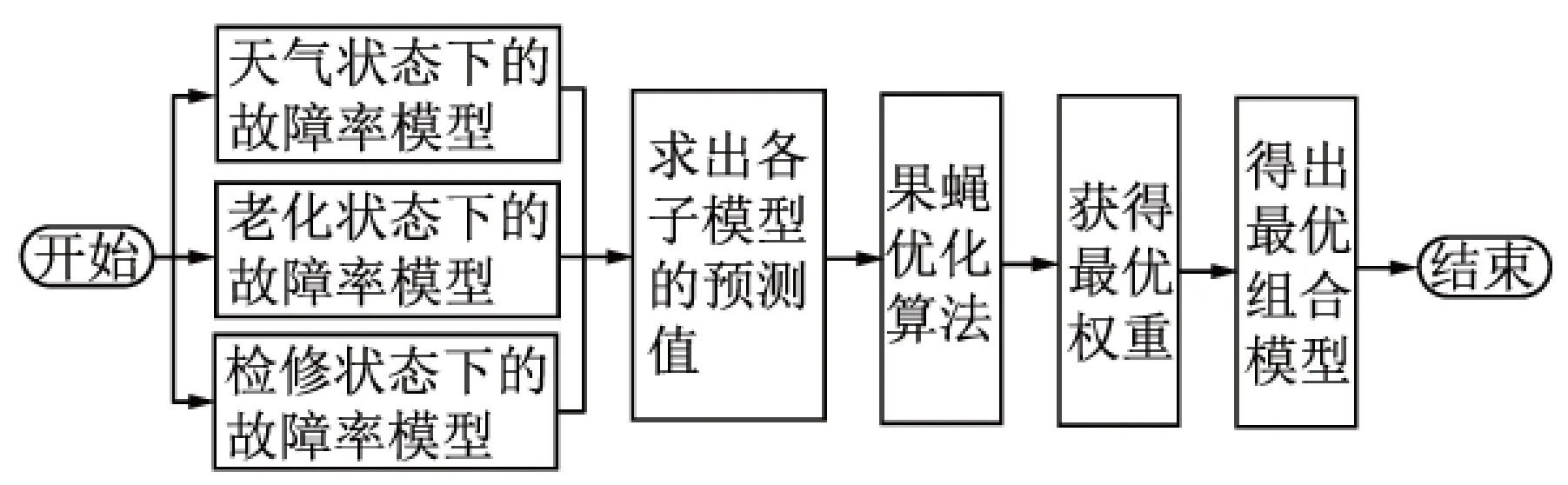
图1　3种状态信息修正优化组合预测流程

1.2果蝇优化算法

果蝇优化算法(fruitflyoptimizationalgorithm,FOA)[10]的核心是果蝇利用其敏锐的感知能力，通过嗅觉搜集各种气味，再发现食物和同伴聚集的位置，沿此方向飞去寻找食物。模仿果蝇搜寻食物的特性，可知果蝇优化算法的建模步骤如下：

步骤1。随机设定果蝇群体的初始位置(x0,y0)，群体规模S，最大迭代次数Nmax；

步骤2。假设Δ为搜寻距离，果蝇根据嗅觉感应随机地飞去寻找目标为

(9)

步骤3。预先估计目标物与原点之间的距离为di，计算出该点处味道浓度判定值Ti，此值是距离之倒数为

(10)

步骤4。结合味道浓度判定值Ti及其判定函数F，计算出果蝇个体位置的味道浓度值

(11)

步骤5。综合分析(4)中的结果,确定该果蝇群体中味道浓度值最大的果蝇

(12)

步骤6。记录并保留最佳味道浓度值ωbi与其X、Y坐标，然后果蝇群体飞向该位置后，即

(13)

步骤7。在遵从最大迭代次数的原则下，进行迭代寻优，重复执行步骤2至步骤5，并判断最佳味道浓度是否优于前一迭代最佳味道浓度，若是，则执行步骤6；否则继续执行步骤2至步骤4，直至找到目标物所在位置。

2　基于多状态信息的电力设备故障率预测模型

2.1设备在天气影响状态下的故障率预测模型

本文综合考虑天气的优劣程度及其对设备的影响，将天气状态划分为正常天气、恶劣天气及极端天气3种，建立3种状态天气模型[11]如图2所示，其中各种天气状态的持续时间可通过相应地区的气象统计数据得到。

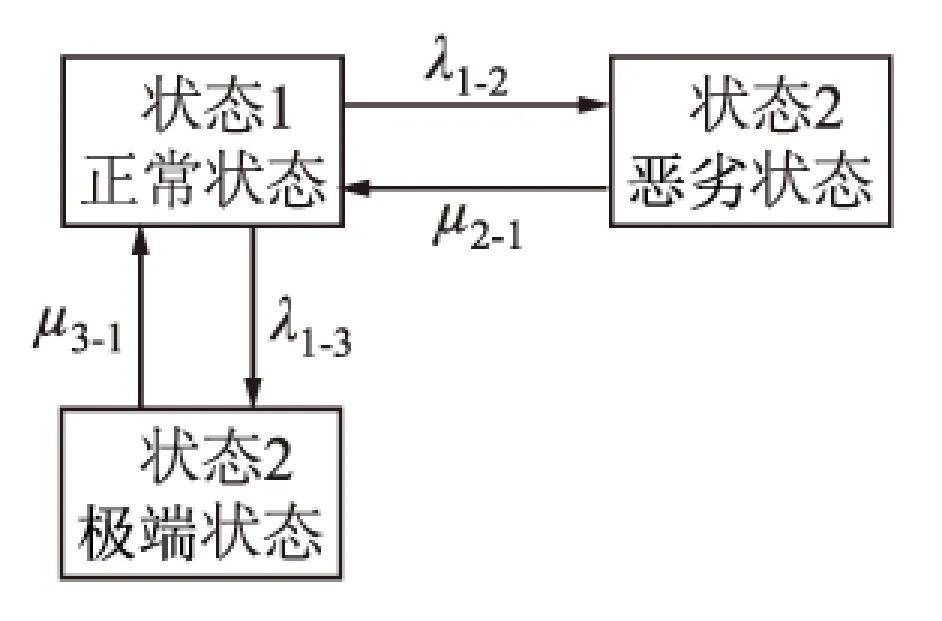
图2　3种状态的天气模型

因为可拓理论能够快速、准确地判断出3种状态天气模型中设备是否发生故障及其程度，且关联函数能够精细化、定量化地预测出设备故障率[8,12-13]。假设设备Ω发生故障，其故障率的具体诊断步骤如下：

步骤1。设Ω可能产生故障Ii(Ω)(i=1,2,…,n)，则其故障集为I={I1(Ω),I2(Ω),…,In(Ω)}。若关于特征cij的经典域和节域分别为Wij=(aij,bij)、Wij′=(aij′,bij′)，则其故障物元集Ri=[Ii(n),cij,Wij](i=1,2,…,n; j=1,2,…,ki)。

步骤2。构建电力设备Ω发生故障时的经典域物元和节域物元分别为

步骤3。建立电力设备Ω待诊状态时的物元

步骤4。求出关联函数值

其中

步骤5。根据最小二乘原理确定各特征的权系数分别为wi1,wi2,…。

步骤7。由步骤6得max{λ[Ii(Ω)]}=λ[I0(Ω)](1≤i≤n)，则可判断设备Ω产生故障I0，且其故障率λ=λ[I0(Ω)]。

2.2设备在绝缘老化状态下的故障率预测模型

2.2.1三参数威布尔分布

三参数威布尔分布[14]更逼近实际，能充分描述设备绝缘老化的失效机理，便于对各影响因素的边际失效概率密度函数f(t1), f(t2),…, f(tn)进行建模分析，其概率密度函数和概率分布函数分别为

(14)

式中：α为尺度参数，可变换横、纵坐标的缩放拉伸程度；β为形状参数，决定了其概率密度曲线的形状；γ为位置参数，表明设备在γ以前不会发生失效。本文采用GM(1,1)预测法来计算模型的三参数值[2]。

2.2.2联合失效概率

设备在绝缘老化状态下的故障率，是指多元随机影响因素的联合失效概率密度在失效域的积分

(15)

式中：f(x1,x2,…,xn)为联合失效概率密度函数；G(x)<0为失效域。

本文采用Copula函数法求解设备老化时的联合失效概率密度，常用的Copula函数类型及其特性和相关概率密度函数表达式参见文献[15]。若存在一个Copula函数C，则有

(16)

设备老化主要受到电场、温度、湿度、机械力、周边环境等因素影响，本文通过建立设备在老化状态下的故障率模型，综合分析该子模型的联合失效概率密度函数f(x1,x2,…,x5)，其求解流程如图3所示。

图3　联合失效概率密度计算流程

2.3设备在检修状态下的故障率预测模型

2.3.1Holt-Winters预测原理

Holt-Winters预测模型适用于分解受季节变化影响较大的设备检修时间序列，估计其长期趋势、趋势增量及季节变量，再推算出故障率。该模型主要由以下3个基本推算公式构成[6]，即

式中：Ut为t时刻的周期项，是未受季节变化影响的时间序列指数平滑均值；bt为t时刻的趋势项，是时间序列变化趋势的指数平滑均值；Ft为t时刻的季节项，是季节因子的指数平滑均值，可消除季节变化对预测值的影响；dt为t时刻的实际值；L为季节长度或时间周期；α、β、γ分别为相应的平滑系数，取值范围限于(0,1)，通常采用迭代法求其最优值，保证了预测结果的可靠性。

故基于Holt-Winters指数平滑模型的预测公式为

(18)

式中Δt为预测时刻与当前时刻的时间间隔数。

本文采用残差值最小化算法确定模型的参数，再对已知数据进行拟合[16]，其具体步骤如下：

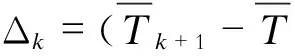
步骤4。算出前k个周期内每个时期的季节因子S(k+1)i=(S1i+S2i+…+Ski)/k。

步骤5。由步骤4所得结果，求出正态化季节因子S=nS(k+1)i/A,A=S(k+1)1+S(k+1)2+…+S(k+1)n。

步骤6。初步预测出第k+1个周期中每个时期的检修时间Ti+j=(E0+j×Δk)×S,(j=1,2,…,n)。

步骤7。选定一组合理的平滑系数α、β、γ来修正步骤6的预测结果。

步骤8。每算完一个周期得到季节因子后，按步骤5的方法重新正态化。反复修改调整，求得较理想结果。

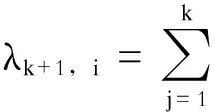
3　实例仿真

本文基于电力设备故障率的多状态修正优化组合预测模型，对某一地区供电线路和变压器历史运行数据统计，相关数据如图4至图6所示，选取10年数据序列进行分析，其中前9年作为设备历史故障率相关的比较数据序列，剩余1年表示设备待求故障率的实际数据序列作为验证。

采用可拓诊断方法预测设备在不同天气状态下的故障率，结合图4所示的统计数据，通过建立物元模型，确定关联函数值和权系数，进而求出其关联度，即为预求故障率，其计算结果见表1。

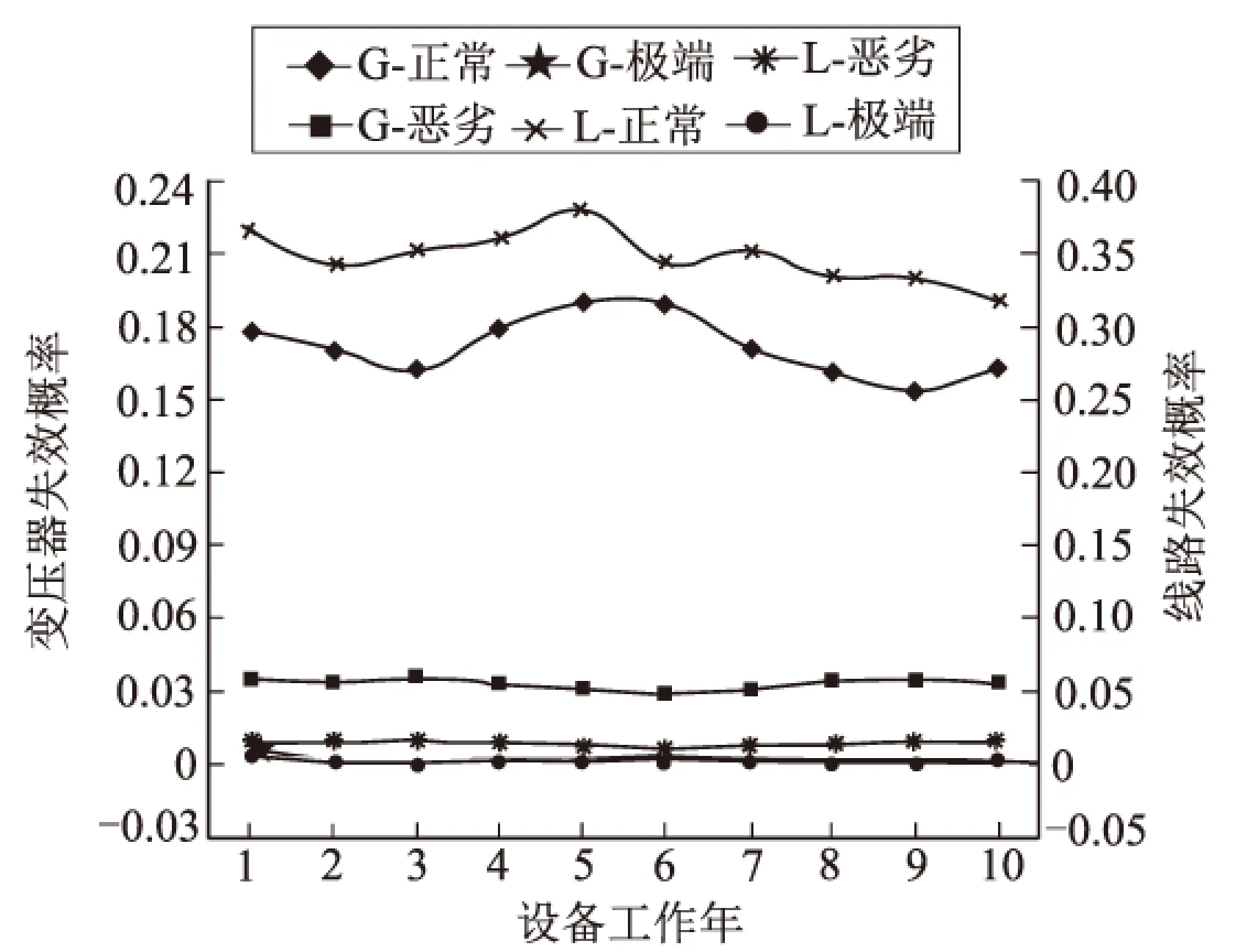
图中的“G”表示发电机；“L”表示线路，下同。图4　电力设备在不同天气状态下的故障率曲线

表1电力设备在天气影响状态下的故障率及误差分析%

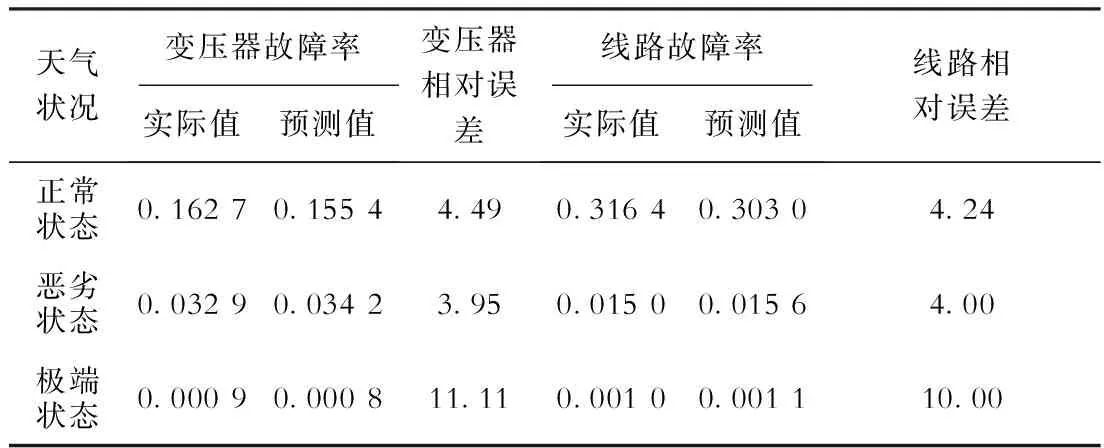
天气状况变压器故障率实际值预测值变压器相对误差线路故障率实际值预测值线路相对误差正常状态0.16270.15544.490.31640.30304.24恶劣状态0.03290.03423.950.01500.01564.00极端状态0.00090.000811.110.00100.001110.00

由表1可知，设备故障率的预测值在正常天气状态和恶劣天气状态下的可靠性较高，相对误差均低于5%；而在极端天气状态下，天气变化大，导致预测结果偏差较大，相对误差均约为10%；整体预测结果的可靠度高，相对误差均低于15%;

结合图5所示统计数据，采用联合失效概率密度法预测设备受绝缘老化影响时的故障率，结果见表2。

图5　电力设备在不同绝缘老化因素影响下的故障率曲线

表2电力设备在绝缘老化状态下的故障率及误差分析%

变压器失效率实际值预测值变压器相对误差线路失效率实际值预测值线路相对误差3.14×10-23.27×10-24.149.23×10-28.86×10-24.01

由表2可知,电力设备在绝缘老化状态下的故障率预测值准确度较高，相对误差均低于5%，故可用该预测值来估算设备的故障率，从而判断出设备出现故障的可能性，及时采取有效措施，提高供电可靠性；结合图6所示的统计数据，采用三参数Holt-Winters模型预测设备在检修状态下的故障率，其预算结果如图7所示。

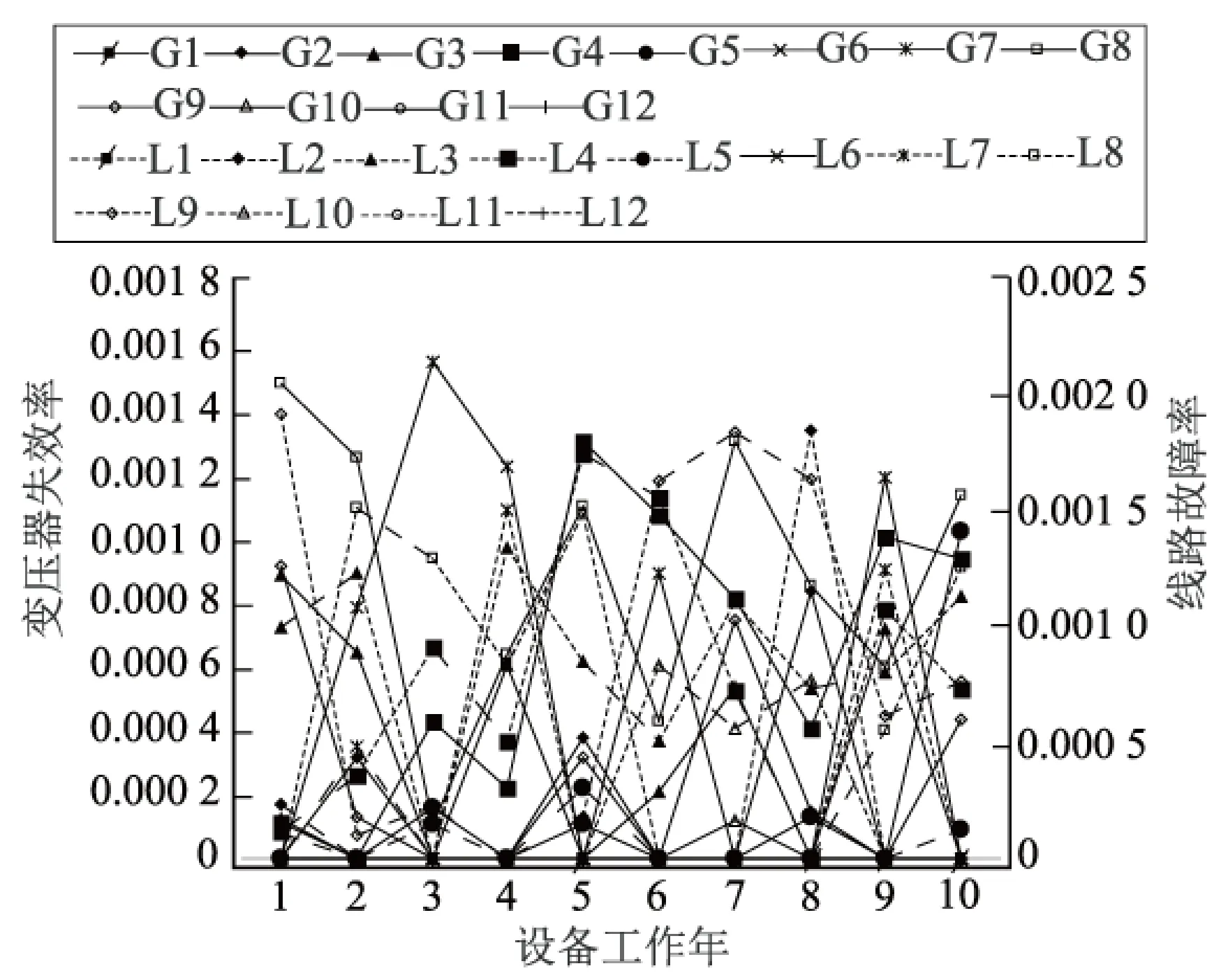
图6　电力设备在检修状态下的故障率曲线

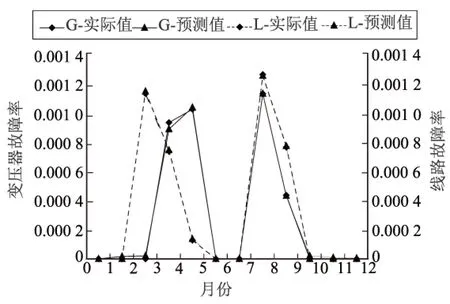
图7　电力设备在检修状态下单月的故障率曲线

由图7可知，该预测模型适合估算受季节变化影响较大的设备检修时间序列，其预算值非常接近实际值，结果有较高的可靠度，故可用该模型来预测设备在检修状态下的故障率，便于安排设备的检修工作。

求出电力设备在修正优化组合预测模型中的故障率结果见表3。

表3电力设备在修正优化组合预测模型中的故障率及误差%

变压器故障率实际值预测值变压器相对误差线路故障实际值预测值线路相对误差0.00410.00459.760.06230.06260.48

由表3可知，根据修正优化组合预测原理预算电力设备故障率的结果的相对误差均低于10%，适用于预测设备在受天气因素、材料绝缘老化和设备检修三者因素综合影响下的故障率，方便准确判断出现故障的可能性及实施保护和控制措施，保证供电可靠性。

另外，以电力设备实际故障率为参照，采用反向传输神经网络-灰色常规组合模型对该设备的故障率进行预测，以其预算结果作为对比数据，具体情况见表4。

由表4可知，常规组合预测模型的计算结果可靠性较本文所提出的修正优化组合预测模型要低，相对误差也较高，故某一些故障率的预测方法并不一定适应于预测所有的随机影响因素造成的故障率，若将其强加于某一个预测模型上，会导致预测结果的可信度降低，从而不能准确判断出设备出现故障的可能性、有效地预防及控制故障。

表4电力设备在不同预测模型中的误差数据比较%

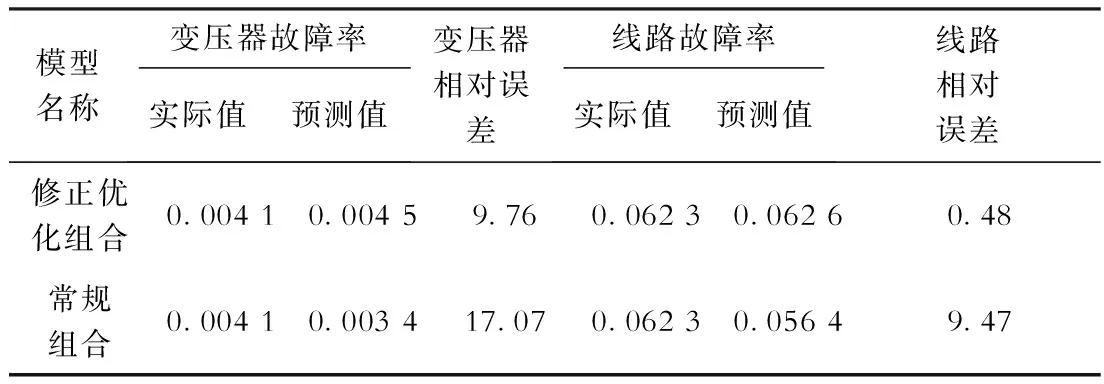
模型名称变压器故障率实际值预测值变压器相对误差线路故障率实际值预测值线路相对误差修正优化组合0.00410.00459.760.06230.06260.48常规组合0.00410.003417.070.06230.05649.47

4　结论

a) 修正优化组合预测值可靠度高，方便人们做出准确的故障判断，及时采取有效的预防和维护措施；

b) 修正优化组合预测法能更好适应电网现代化发展，其应用范围广、预测过程简便、求解效率高，适用于估算复杂约束条件下的设备故障率；

c) 修正优化组合预测模型先以单个约束条件作为预测目标，再通过果蝇算法优化融合以削弱参数变化对预测精度的影响，其预测结果较其他传统方法优异，并克服了常规组合预测法的多种弊端。

[1]BATESJM,GRANGERCWJ.CombinationofForecasts[J].OperationsResearchQuarterly, 1969, 20(4): 451-468.

[2]张肖波, 李婧娇, 罗欣. 基于灰色关联分析与人工神经网络算法的节假日负荷预测研究[J]. 广东电力, 2012, 25(7): 38-42.

ZHANGXiaobo,LIJingjiao,LUOXin.ResearchonLoadForecastonHolidaysBasedonGreyRelationalAnalysisandArtificialNeuralNetworkAlgorithm[J].GuangdongElectricPower, 2012, 25(7): 38-42.

[3]占才亮. 人工智能技术在电力系统故障诊断中的应用[J]. 广东电力, 2011, 24(9): 87-92.

ZHANCailiang.ApplicationofAITechnologyinFaultDiagnosisofPowerSystem[J].GuangdongElectricPower, 2011, 24(9): 87-92.

[4]陈永进, 任震, 黄雯莹. 考虑天气变化的可靠性评估模型与分析[J]. 电力系统自动化, 2004, 28(21): 17-21.

CHENYongjin,RENZhen,HUANGWenying.ModelandAnalysisofPowerSystemReliabilityEvaluationConsideringWeatherChange[J].AutomationofElectricPowerSystems, 2004, 28(21): 17-21.

[5]赵玉林. 高电压技术[M]. 北京: 中国电力出版社, 2008.

[6]吴越强, 吴文传, 李飞, 等. 基于鲁棒Holt-Winters模型的超短期配变负荷预测方法[J]. 电网技术, 2014, 38(10): 2810-2815.

WUYueqiang,WUWenchuan,LIFei,etal.Ultra-shortTermLoadForecastingUsingRobustHolt-WintersinDistributionNetwork[J].PowerSystemTechnology, 2014, 38(10): 2810-2815.

[7]蔡菲, 严正, 赵静波, 等. 基于Copula理论的风电场间风速及输出功率相依结构建模[J]. 电力系统自动化, 2013, 37(17):9-16.

CAIFei,YANZheng,ZHAOJingbo,etal.DependenceStructureModelsforWindSpeedandWindPoweramongDifferentWindFarmsBasedonCopulaTheory[J].AutomationofElectricPowerSystems, 2013, 37(17): 9-16.

[8]李存斌, 李小鹏, 高坡. 基于变权模糊物元模型的变压器状态实时评估[J]. 广东电力, 2015, 28(11): 66-73.

LICunbin,LIXiaopeng,GAOPo.Real-timeEvaluationonTransformerStateBasedonVariableWeightFuzzyMatter-elementModel[J].GuangdongElectricPower, 2015, 28(11): 66-73.

[9]王洪森, 彭显刚. 基于进化和声搜索优化的短期风速组合预测方法[J]. 广东电力, 2013, 26(12): 26-30.

WANGHongsen,PENGXiangang.Short-timeWindSpeedCombinedPredictionMethodBasedonEvolutionalandHarmonySearchOptimization[J].GuangdongElectricPower, 2013, 26(12): 26-30.

[10]PANWT.ANewFruitFlyOptimizationAlgorithm:TakingtheFinancialDistressModelasanExample[J].Knowledge-basedSystems, 2012, 26: 69-74.

[11]BILLINTONR,ACHARYAJR.Weather-basedDistributionSystemReliabilityEvaluation[C]//ProceedingsofIEEEGeneration,TransmissionandDistributionConference.Stevenage,UK:IEEE, 2006: 499-506.

[12]蔡文. 物元模型及应用[M]. 北京: 科学技术文献出版社, 1994.

[13]邓宏贵. 可拓理论与关联分析及其在变压器故障诊断中的应用[D]. 长沙: 中南大学, 2005.

[14]王松岩, 于继来. 短时风速概率分布的混合威布尔逼近方法[J]. 电力系统自动化, 2010, 34(6): 89-93.

WANGSongyan,YUJilai.ApproximationofTwo-peakWindSpeedProbabilityDensityFunctionwithMixedWeibullDistribution[J].AutomationofElectricPowerSystems, 2010, 34(6): 89-93.

[15]NELSENRB.AnIntroductiontoCopulas[M]. 2ed.NewYork,NY,USA:Springer, 2006.

[16]李晓童.Holt-Winters模型与X-11模型在预测中的比较研究[J]. 张家口师专学报, 2000, 16(2): 70-73.

LIXiaotong.ComparisonofHolt-WintersModelsandX-11ModelsinPrediction[J].JournalofZhangjiakouTeachersCollege, 2000, 16(2): 70-73.

(编辑王夏慧)

Calculation Method for Fault Rate of Electric Power Equipment Based on Multi-state Information Amendment Optimization Combination

WU Jiekang, XU Zhiqiang, XU Qingzhuo, BAO Yuhui

(School of Automation, Guangdong University of Technology, Guangzhou, Guangdong 510006, China)

Forecasting method for multi-state information amendment optimization combination is used to establish three kinds of models of state amendment optimization combination for forecasting fault rates of electric power equipments, which are respectively affected by weather, insulation aging of materials and equipment overhaul. In allusion to characteristics of various stochastic influencing factors, extensible principle is applied in forecasting fault rates of three kinds of weather state models. Joint failure probability density method based on three parameters Weibull distribution-Copula function is used for calculating fault rate caused by insulation aging and Holt-Winters model is used to estimate fault rate due to equipment overhaul. Predicted value with high degree of accuracy is worked out by using fruit flies optimization algorithm to weight and optimize the fault rate of each submodel. Taking one power system in some region for an example, the analysis results indicate that these models can effectively improve forecasting precision of fault rates, meanwhile the fruit flies optimization algorithm is efficient to solve the forecasting problem of multi-state information amendment optimization combination.

electric power equipment; fault rate; multi-state information; amendment optimization combination; fruit flies optimization algorithm

2016-03-14

2016-05-25

国家自然科学资助基金(50767001);国家863高技术资助基金(2007AA04Z197);广东自然科学资助基金(S2013010012431, 2014A030313509);中国南方电网有限责任公司科技项目(K-GD2014-194)

10.3969/j.issn.1007-290X.2016.08.012

TM732

A

1007-290X(2016)08-0060-07

吴杰康(1965)，男，广西隆安人。教授，工学博士，主要研究方向为电力系统运行与控制。

胥志强(1990)，男，江西丰城人。在读硕士研究生，主要研究方向为电力系统运行与控制。

徐庆焯(1991)，男，广东佛山人。在读硕士研究生，主要研究方向为电力系统运行与控制。