某圆形地下连续墙基础施工阶段数值模拟分析研究

曹　峰，张东东

(中交第二公路工程局有限公司，陕西　西安　710065)



某圆形地下连续墙基础施工阶段数值模拟分析研究

曹峰，张东东

(中交第二公路工程局有限公司，陕西西安710065)

文章通过使用Midas/GTS有限元软件对某锚碇圆形地下连续墙基础在不同开挖方式下的应力、应变及地下连续墙应力、应变对结构几何尺寸的敏感性进行数值模拟，分析地下连续墙桥梁工程施工阶段的特点。结果表明，采用平挖方案和不对称开挖方案时，地下连续墙的变形及应力均能满足施工监测预警值要求，不会使得支护结构产生较大变形。

锚碇；圆形地下连续墙；开挖方式；数值模拟

0　引言

地下连续墙已发展60多年，随着新材料、新机械、新技术的发展，已广泛应用于各种地下构筑工程、水利工程、市政工程等。使用该类型基础可以加快施工速度、降低工程费用，还能在施工中降低噪音、减少振动，并能在接近已有建筑物的附近施工[1-2]。其之所以能加速施工和降低成本，主要是简化了施工。本文主要通过对某锚碇圆形地下连续墙基础施工方案的数值分析，阐述地下连续墙桥梁工程施工阶段的特点。

1　工程概况

某锚碇基础采用地连墙方案作为基坑开挖的支护结构，根据地质情况及锚体设计需要，地连墙采用外径为82.0 m，壁厚为1.5 m的圆形结构，底标高-35.00～-43.00 m，底部嵌入中风化泥岩、泥质粉砂岩层；地连墙分Ⅰ期、Ⅱ期两种槽段施工，槽段共54个，设计最大槽深46.0 m。

地连墙施工完成后，采用逆作法分层开挖土体，分层施工内衬。土体开挖深度为27 m，土体开挖主要采取平挖方案，内衬及土体分层高度控制在3 m以内。考虑到施工组织的要求，对局部采取超挖3 m、不对称开挖等方案。

2　锚碇基础三维数值模型的建立

本文使用MIDAS/GTS 4.0版本对基坑进行三维数值模拟并分析该基坑在各工况下的应力应变关系。为了满足计算精度的要求，选择Midas.GTS中土体的摩尔-库伦本构模型能够很好地反映出土体的弹塑性特征，在计算区域上需要考虑足够的计算范围。由工程概况确定建立计算模型为：长240 m，宽240 m，深80 m。模型共划分单元36 000个，节点总数为110 000个。

地下连续墙基坑整体网格模型如图1～3所示。

图1　基坑模型网格图

图2　地下连续墙结构网格图

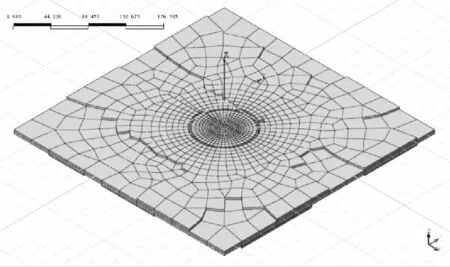
图3　异型土层局部网格图

根据地质勘察报告，基坑开挖岩土体及支护结构物理参数值见表1。

3　施工工况模拟

3.1平挖施工方式

坑内开挖土体及内衬共分9层，每次开挖土体及施工内衬高3 m，土体开挖与内衬同时施工。具体施工顺序如图4所示，对施工过程进行数值模拟。

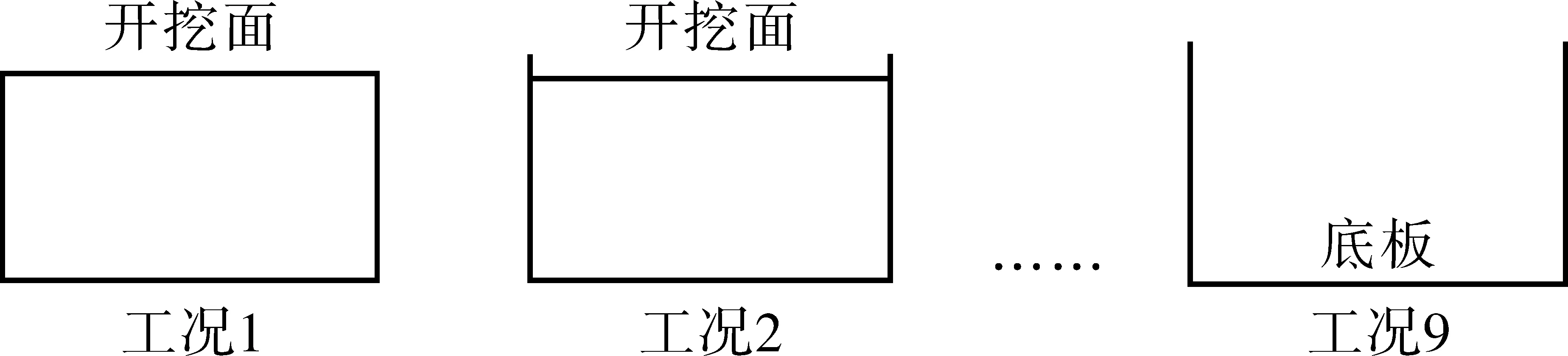
图4　基坑纵向施工过程顺序图(图中蓝色部分为内衬)

基坑在开挖过程中，围护结构受水、土应力影响，产生变形。图5给出基坑在开挖完成后围护体系的应力应变云图。

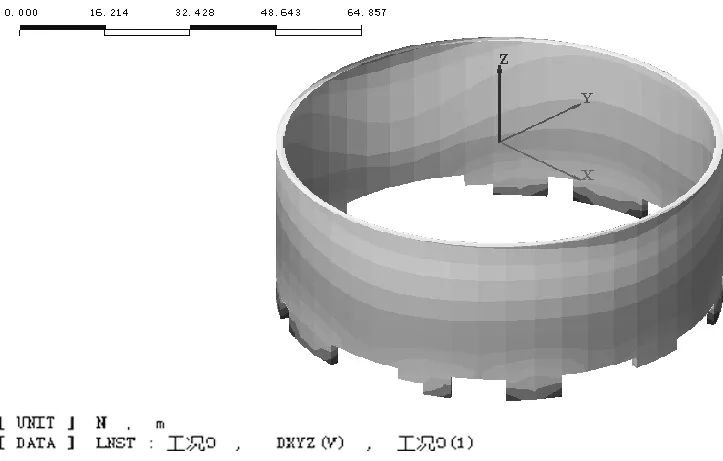
(a)开挖完成后地连墙水平位移

(b)开挖完成后地连墙正应力

经数值分析，基坑在开挖过程中产生了不同程度的变形，基坑在各工况状态下围护结构的应力应变水平[3]见表2。

从表2可知，随着基坑开挖深度的增加，围护结构的应力和其对应的水平位移逐渐增大，当基坑开挖完成后，围护结构的最大累计位移为6.18 mm(小于规范要求30 mm预警值)。

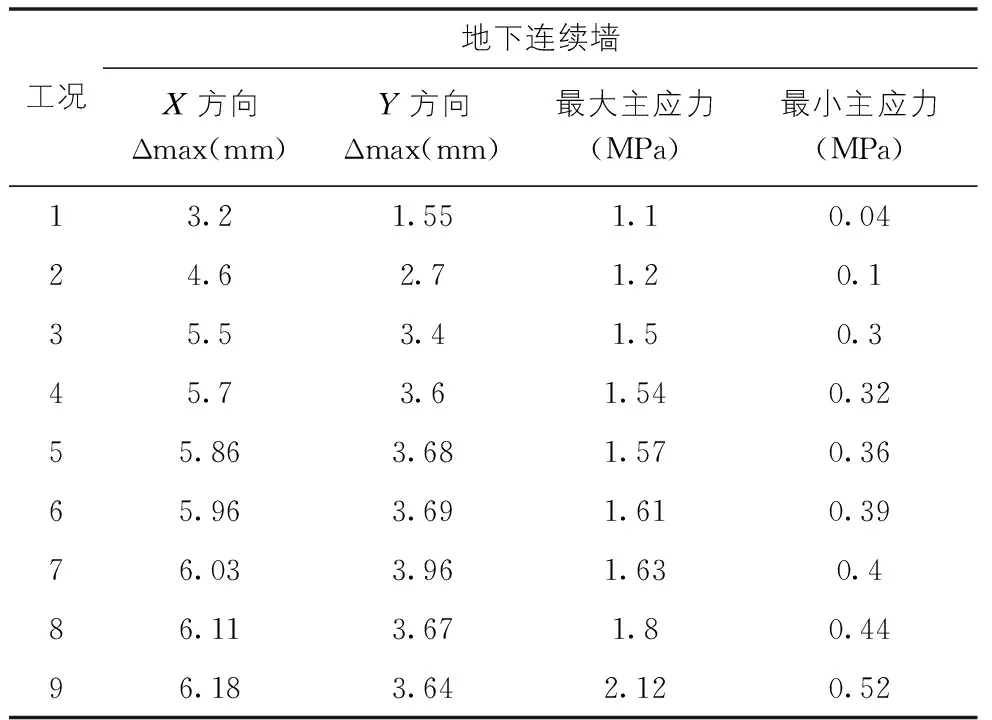
表2　基坑开挖过程中围护结构应力应变状况表

3.2不对称开挖施工方式

不对称开挖方案是将岛式开挖方案分为若干部分并分别对预设区段进行依次开挖。对该方案的数值分析采用先开挖每层1～7部位，再开挖8～14部位，最后将中心60 m圆形区域开挖，当一层开挖完毕后按照相同顺序对下层土体进行开挖[4]。

该方案的单层开挖顺序如图6所示，各区段施工按照数字由大到小依次进行开挖，且图中阴影部分为已开挖部位。

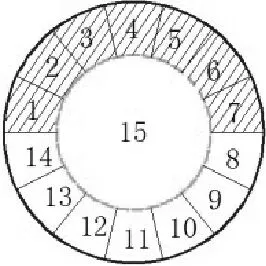
(a)

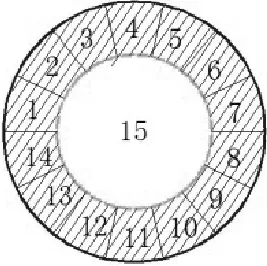
(b)

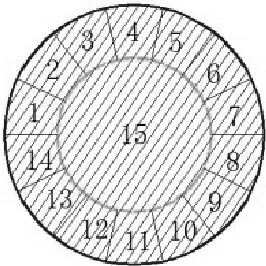
(c)

按照图6开挖方案对每工况的开挖进行数值模拟计算。结果显示：在不对称开挖方案条件下，最不利工况(工况9)下地连墙X方向最大水平位移为6.084 mm，Y方向最大水平位移为3.426 mm，地连墙最大压应力为2.74 MPa。相对于平挖开挖方案，其地连墙X方向最大位移降低0.312 mm；地连墙Y方向最大位移降低0.361 mm；最大压应力降低0.22 MPa。采用不对称开挖使地连墙水平位移及最大压应力有较小幅度的降低，应力水平满足材料设计强度要求，根据计算值在实际中不会引起支护体系的破坏。

3.3地连墙支护结构敏感性分析

为考虑支护结构的施工变形效应，该方案将支护体系平面形式由半径为82 m的圆形转换为椭圆形，椭圆长轴为r(1+5%)，短轴为r(1-5%)，即长轴长84 m，短轴长76 m。

围护结构平面图如图7所示。

图7　围护结构平面示意图

在变形围护方案条件下，基坑开挖数值计算结果为：最不利工况(工况9)下地连墙X方向最大水平位移为5.52 mm，Y方向最大水平位移为7.06 mm，地连墙最大压应力为2.84 MPa。支护结构几何尺寸变形后地连墙水平位移及最大主应力有较小幅度增加或减小，应力水平满足材料设计强度要求，根据计算值在实际中不会引起支护体系的破坏，说明在实际的施工过程中围护结构几何尺寸发生微小变形对支护结构变形的敏感性不显著，影响很小，在施工中可以不考虑几何尺寸微小变形对支护结构的影响。

3.4超挖方案分析

为考虑施工过程中架设衬砌所需要的足够空间，需对基坑超挖进行数值分析，以预防该基坑在超挖工况下围护结构出现较大变形[5]。

结合施工条件，在与设计方和施工方讨论之后，对该工程进行超挖预测，超挖规则按照每工况在岛式开挖基础上开挖深度下沿3 m，且超挖3 m为无内砌支护临空裸露状态。工况8至工况9的开挖顺序见图6，当开挖至工况8时，对称开挖方案下该基坑应挖至24 m处。在超挖方案下，该工况基坑开挖深度为27 m，且0～24 m采用内衬支护，25～27 m部位未设置内衬，即此3 m为无内衬支护的“临空无撑”部位，详细示意图如图8所示。

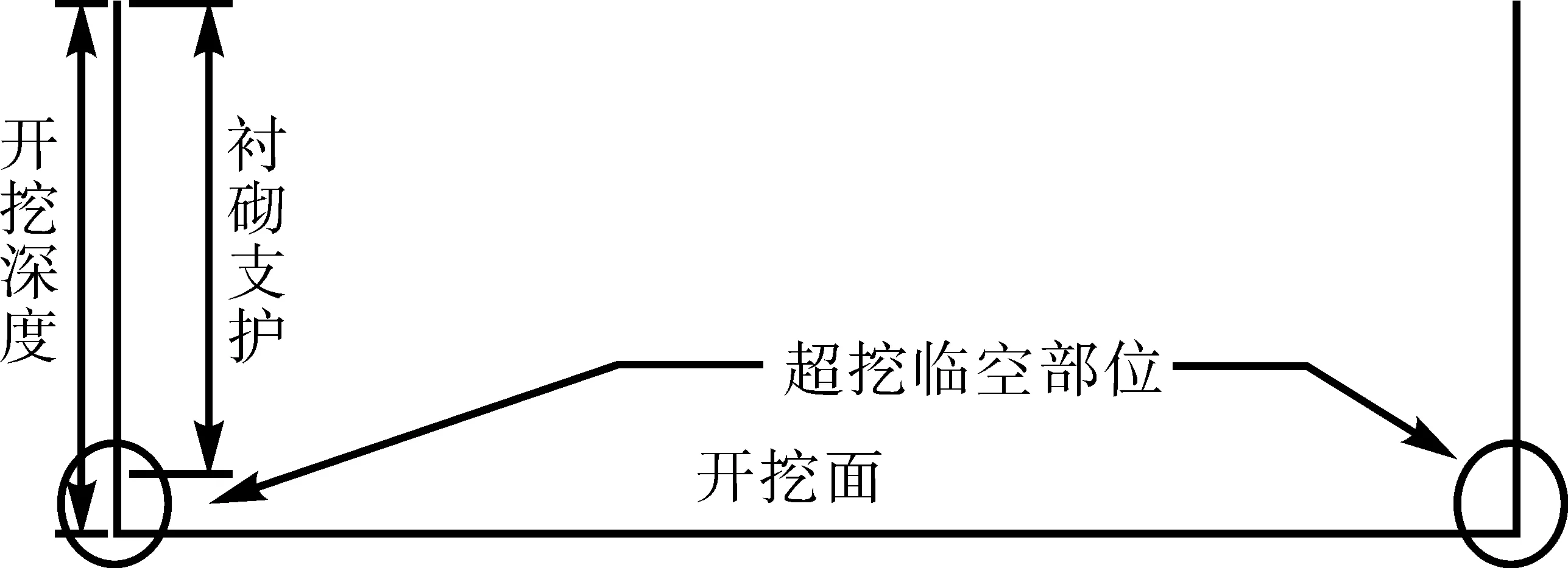
(a)工况8

(b)工况9

按照图8开挖方案对每工况的开挖进行数值模拟计算，结果显示：在超挖方案条件下，最不利工况(工况9)下地连墙X方向最大水平位移为6.72 mm，Y方向最大水平位移为4.29 mm，地连墙最大压应力为2.33 MPa。

采用超挖方式使地连墙水平位移及最大主应力有较小幅度增加，应力水平满足材料设计强度要求，不会引起支护体系的破坏，说明在实际的施工过程中采用超挖方式是可行的。

4　结语

(1)通过数值模拟结果可以得出，采用平挖方案、不对称开挖方案及部分超开挖时，地连墙的最大水平位移及最大应力均能满足材料设计强度要求和监测预警值要求，根据计算值在实际中不会引起支护结构的破坏，不会使得支护结构产生较大变形。可采用该两种方案进行实际施工。

(2)地连墙结构几何尺寸发生微小变化对地连墙的水平变形和应力影响很小，说明地连墙结构应力、应变对几何尺寸发生微小变形的敏感性不显著。在实际施工，地连墙结构因施工原因产生微小施工误差是允许的。

(3)数值模拟对施工起到了预测的作用，随着施工的进行，不断累积现场观测数据，不断反演计算，辨识土体新的等效参数，建立更加完整的空间模型为后续施工提供指导作用。

[1]李云安，葛修润，张鸿昌.深基坑工程变形控制与有限元数值模拟分析[J].地质与勘探，2001，37(5)：73-76.

[2]龚晓南，高有潮.深基坑工程设计施工手册[M].北京：中国建筑工业出版社，2001.

[3]邵敏，等.有限元法基本原理与数值方法[M].北京：清华大学出版社，2002.

[4]柏国利.圆形地下连续墙壳体有限元数值模拟分析[D].上海：同济大学，2006.

[5]田蓓蕾.基于变形控制的深基坑地下连续墙支护数值模拟研究[D].武汉：湖北工业大学，2012.

Numerical Simulation Analysis on Foundation Construction Stage of A Cir-cular Diaphragm Wall

CAO Feng，ZHANG Dong-dong

(CCCC Second Highway Engineering Co.，Ltd.，Xi’an，Shaanxi，710065)

By using Midas/GTS finite element software，this article conducted the numerical simulation for the stress，strain and diaphragm wall stress，and the sensitivity of strain to structure geometry of circular diaphragm wall foundation of an anchorage under different excavation methods，and analyzed the fea-tures of diaphragm wall bridge construction phase.The results showed that，when using the flat excava-tion program and asymmetrical excavation program，both deformation and stress of diaphragm wall can meet the requirements of construction monitoring and warning value，and the supporting structure has no greater deformation.

Anchorage；Circular diaphragm wall；Excavation method；Numerical simulation

U445.55

A

10.13282/j.cnki.wccst.2016.03.018

1673-4874(2016)03-0065-05

2016-03-02

曹峰(1982—)，硕士研究生，工程师，研究方向：公路项目试验检测，施工监控、监测等；

张东东(1983—)，硕士研究生，工程师，研究方向：公路项目桥梁设计、变更等。