城市大规模交通网络低效路段组合定位及分析
孙黎,凌溪蔓,谭倩,王璞
(中南大学 交通运输工程学院,湖南 长沙 410000)

城市大规模交通网络低效路段组合定位及分析
孙黎,凌溪蔓,谭倩,王璞
(中南大学 交通运输工程学院,湖南 长沙 410000)
基于布雷斯悖论现象,根据城市交通网络中路段或路段组合对路网通行效率的影响,可将其划分为低效的或必要的,合理关闭路网中的低效路段及路段组合将减少所有出行者的出行时间成本,必要路段及路段组合的关闭将增加出行者额外的出行延误。采用改进的自适应遗传算法以有效地定位大规模真实交通网络中的低效路段组合,结合美国旧金山市大规模实际交通网络地理信息系统(GIS)数据以及该区居民通勤出行数据进行实证分析。研究结果证实低效路段和必要路段的组合可能是低效的。分析表明,低效路段组合的低效程度|ΔTS|随着所含路段数量增加呈现先增后减的变化趋势,含路段数相对少的低效路段组合对路网效率产生更大的影响也更普遍。
城市交通效率;布雷斯悖论;大规模交通网络;自适应遗传算法
1968年,德国数学家Braess提出交通网络中的布雷斯悖论现象[1],即在拓扑结构确定的网络中,当网络中的流量分配达到均衡时,增加一条连边,改变该网络的拓扑结构,非但不会减少出行者的出行成本,反而增加该网络中所有用户的出行成本。该现象为治理城市交通拥挤提供了新的思路。2008年,Youn[2]认为由于出行者总是期望个人出行费用最低,使得系统需要额外损失将近30%的出行成本。1984年,Dafermos等[3]现了道路交通网络中路段阻抗随着路网中交通需求改变和路段数量增加而变化的规律。在此基础上,Pas等[4]的研究发现路网中的布雷斯悖论现象与路阻函数参数取值和交通需求量有关,并提出悖论现象只会在特定的交通需求总量下发生。Hagstrom等[5]分析了布雷斯悖论现象在简单网络中的发生机制。直到2010年,Nagurney[6]用数学推导证实在非常大的交通需求下,布雷斯悖论现象随即消失,并以“群体智慧”解释了这一现象。Roughgarden[7]的研究表明大规模复杂交通网络中基于布雷斯悖论研究网络结构最优化是一类NP难问题,实际上随着网络规模的增大,寻求该问题的最优解越难实现。由于大规模实际数据难以获取,布雷斯悖论的相关研究大多以理论模型为基础,关于真实数据的仿真分析相对有限。2014年,Bagloee等[8]利用加拿大温尼伯的路网数据提出了一个利用启发式算法搜索路网低效路段的计算模型。Sun等[9]研究了大规模实际道路交通网络低效路段及其属性特征,提出路网中低效路段的数量和分布与交通流的不均匀分布密切相关。本文作者提出改进的低效路段组合启发式定位算法,并对低效路段组合属性进行了深入分析。

1 问题描述
根据布雷斯悖论现象的描述,悖论现象的产生是由于网络中的纳什均衡往往偏离帕累托最优[10],即个体所追求的效益最大化并非系统最优,新增道路看似能为出行者提供便利,却适得其反。1990年,纽约市决定临时关闭该市最繁忙路段之一的第42号大街一天,结果该市的车辆通行反而比平时更为顺畅。一项调查表明,波士顿的6条公路,曼哈顿的12条公路以及伦敦中部的7条公路如果关闭,或可减少车辆的平均出行时间[11]。由此可见,在特定的交通流下,既有的城市道路交通网络总是存在一些低效路段,关闭这些路段反而能提高整个网络的通行效率,减少每个出行者的出行时间。

2 定位低效路段及其组合的算法
2.1用户均衡算法
出行者在路网中总是基于个人出行成本最优选择出行路径,此时网络中所有出行达到纳什均衡[12-13]。假设所有出行者对路网都非常熟悉,并选择从起点到终点之间出行时间最小的径路,只有当不存在出行者能单方面改变其径路来降低其行驶时间,出行分布即达到均衡状态。为计算均衡状态下各个路段上的车流量fi以及各路段的行驶时间ti(fi),这里采用用户均衡的Beckmann模型进行求解[14],即出行分布达到均衡时满足:
(1)
ti由BPR方程求解得出:
(2)
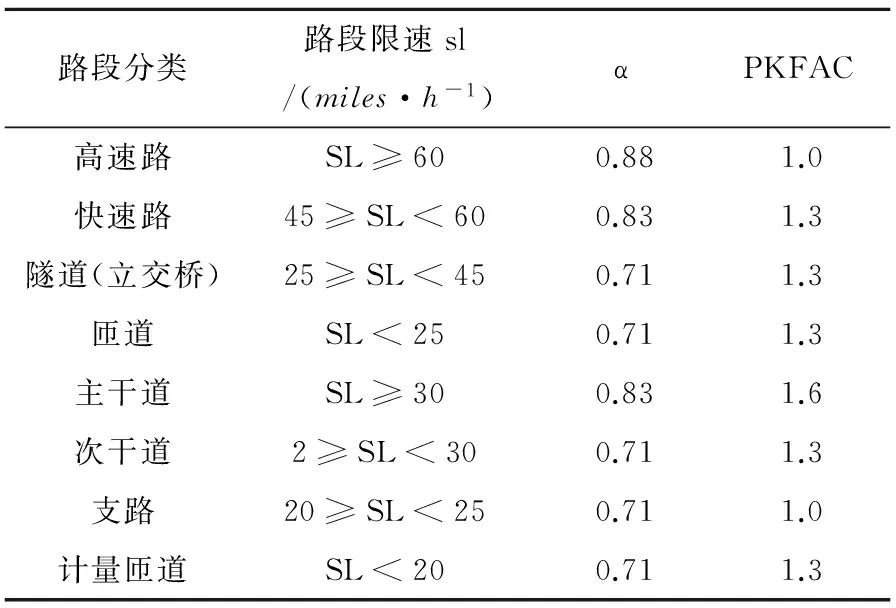
表1 各等级路段PKFAC以及α的取值表[19]
2.2低效路段组合定位算法
近年来,启发式算法被广泛应用到路径优化[20],资源调配[ 21]等组合优化问题中。本文采用改进的自适应遗传算法定位大规模真实道路交通网络中的低效路段组合。首先,需要计算初始网络G0中各路段属性,具体步骤为:
步骤1:初始化,将既有路网定义为初始状态G0,求解在满足用户均衡的条件下G0中所有出行的出行总时间T,i=1,开始迭代;
步骤2:计算路段ei是否为关键路段,如果是,i=i+1继续步骤2,否则转入步骤3;
步骤3:在初始状态中关闭路段ei,得到新路网Gi,求解在满足用户均衡状态下所有出行在路网Gi的出行总时间Ti,并计算ΔTi。若ΔTi<0,则ei为低效路段,否则,ei为必要路段。
步骤4:迭代终止条件:如果满足i=n则停止迭代;否则i=i+1返回步骤2。
通过以上步骤,可以将G0中的路段划分为关键路段集合Ec,必要路段集合En,以及低效路段集合Ei。以必要路段和低效路段集合组成路段集Et,各路段按ΔTi从小到大排序,并对路段重新编号,编号从1到m,其中m表示Et中的路段总数。Ec中各路段的编号从m+1到n。
其中计算网络中路段ei是否为关键路段的具体方法为:
1)在路网G0中去除路段ei,并利用Dijkstra算法计算所有出行的起点和终点之间的最短路径。
2)如果出行中存在至少一对起终点之间的最短路径长度为无穷大,则表明路段ei为关键路段。否则路段ei为非关键路段。


(3)
算法的具体步骤:
步骤1:计算初始解
从G0的低效路段集合Ei中随机选择Q个低效路段构成的初始解集P(0)。其中,每个个体sq只有一个路段处于关闭状态(且均为低效路段)。t=1,i=1开始迭代。
步骤2:选择操作
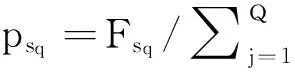
步骤3:交叉操作
对步骤2选择的两个父代个体,按照式(4)中的pc进行交叉操作,生成两个新个体;
(4)
式中:pc1=0.9,Fmax为父代种群中的最大适应度值;Fave为父代种群的平均适应度值;F*为进行交叉的两个父代个体中较大的适应度值;pc2表示父代种群中具有最大适应度值的个体的交叉概率。
步骤4:变异操作
对步骤3生成的两个新个体,依据变异概率pm进行变异操作,得到第t代解集P(t)的两个解st(i)和st(i+1)。
步骤5:收敛性判断
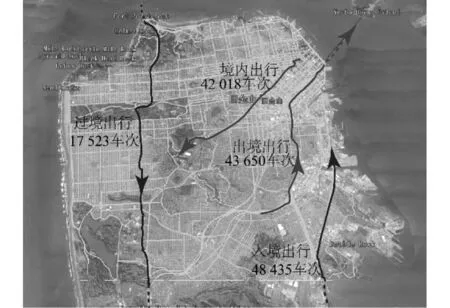
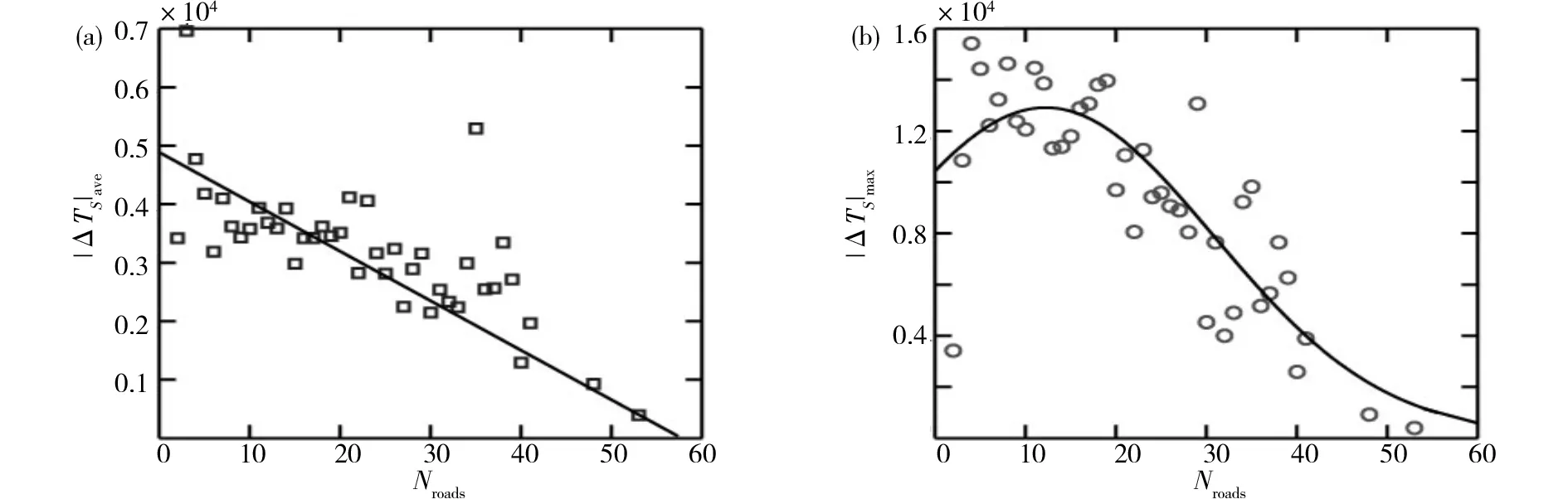
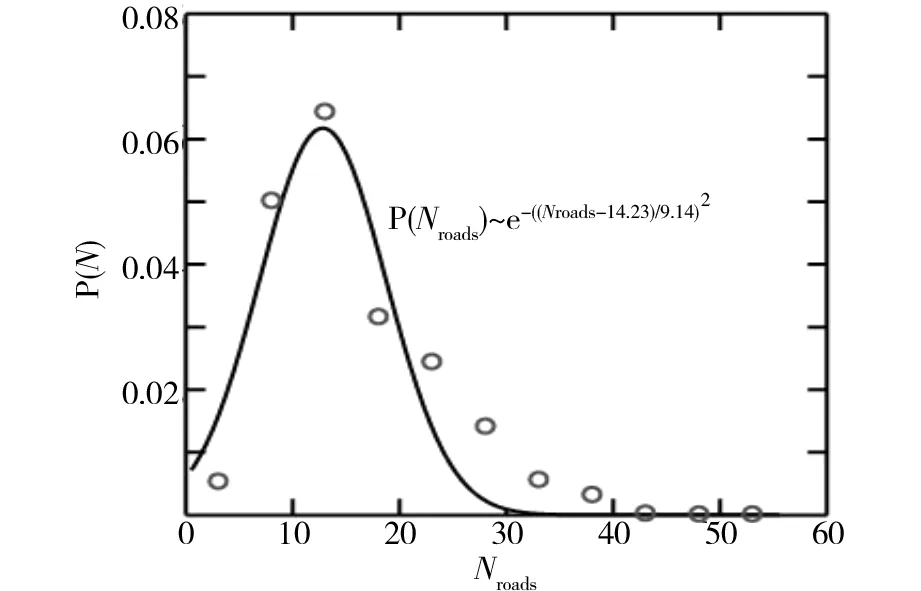
如果i+1=Q且t 3.1旧金山市道路网络基本信息 图1 旧金山市地理网络和出行数据Fig.1 Transport network and traffic in San Francisco 3.2旧金山市道路网络的低效路段 根据3.1中用户均衡算法将4.1中旧金山市早高峰小时通勤出行分布到路网G0,得到各路段的车流量fi如图2所示。 图2 旧金山市早高峰小时通勤出行流量分布图Fig.2 Traffic flow distribution of San Francisco during the morning peak 采用3.2中计算路网各路段属性的步骤,得出旧金山市城市道路交通网络G0各属性路段如表2所示。 表2 G0和G109各属性路段对比 3.3旧金山市道路网络的低效路段组合 图3 不同路段数的低效路段组合的|ΔTS|ave以及|ΔTS|max变化曲线Fig.3 Number of roads in inefficient road cluster versus |ΔTS|ave and |ΔTS|max 同时,满意解集对应的路段组合所含路段数的概率密度分布(图4)显示路段组合中Nroads≤20的占比达到75.86%,而Nroads≥40的占比仅为0.3%。整个满意解集对应的路段组合中Nroads的概率密度呈现高斯分布,拟合函数满足P(Nroads)=0.068×e-((Nroads-14.23)/9.14)2,其中(R2=0.95)。进一步说明,Nroads相对较小的路段组合在交通网络中更为普遍,在提高网络运行效率方面的作用也更大。 图4 Nroads 的概率密度图Fig.4 Probability density of Nroads 1)本文实例结果证明,实际道路交通网络中的一些必要路段和低效路段的组合可能是低效的,低效路段组合的低效程度随着组合中路段数的增加呈现出先增后减的变化趋势。 2)低效路段尤其是低效路段组合的研究,对优化交通网络拓扑结构,提高交通网络资源利用率,缓解城市拥挤等具有重要应用价值。同时本研究的相关结论可进一步推广到具有类似拓扑结构特性的复杂网络系统。 3)需要指出的是:虽然自适应遗传算法能较快的搜索大量的可行解,但鉴于问题解的规模较大,难以快速定位到最优解,算法的收敛相对较慢。 [1]BraessVD. ÜbereinParadoxonausderVerkehrsplanung[J].Unternehmensforschung, 1968, 12 (1): 258-268. [2]YounH,GastnerMT,JcongH.Priceofanarchyintransportationnetworks:efficiencyandoptimalitycontrol[J].PhysicalReviewLetters, 2008, 101(12): 128701-128704. [3]DafermosS,NagurneyA.Onsometrafficequilibriumtheoryparadoxes[J].TransportationResearchPartB:Methodological, 1984, 18(2): 101-110. [4]PASEI,PRINCIPIOSL.Braess'paradox:Somenewinsights[J].TransportationResearch, 1997, 31 (3-31): 265-276. [5]HagstromJN,AbramsRA.CharacterizingBraess'sparadoxfortrafficnetworks[C]//ProceedingsoftheIEEEConferenceonIntelligentTransportationSystems, 2001: 837-842. [6]NagurneyA.ThenegationoftheBraessparadoxasdemandincreases:Thewisdomofcrowdsintransportationnetworks[J].EPL, 2010, 91(4): 48002-48006. [7]RoughgardenT.OntheseverityofBraess’sParadox:Designingnetworksforselfishusersishard[J].JournalofComputerandSystemSciences, 2006, 72 (5): 922-953. [8]BagloeeSA,CederA,TavanaM,etal.Aheuristicmethodologytotacklethebraessparadoxdetectingproblemtailoredforrealroadnetworks[J].TransportmetricaA:TransportScience, 2014, 10 (5): 437-456. [9]SUNLi,LIULike,XUZhongzhi,etal.Locatinginefficientlinksinalarge-scaletransportnetwork[J].PhysicaA:StatisticalMechanicsanditsApplications, 2015(419): 537-545. [10]WilliamES,RapoportA,DarrylAS.Batchqueueswithchoiceofarrivals:Equilibriumanalysisandexperimentalstudy[J].GamesandEconomicBehavior, 2007, 59 (2): 345-363. [11] 张薇薇. 少即是多, 从布雷斯悖论引出的话题 [J]. 世界科学, 2014(6): 53-55. ZHANGWeiwei.Lessismore,topicslearnfromBraessparadox[J].WorldScientific, 2014(6): 53-55. [12]KubeS,SeltenR,ChmuraT,etal.Commutersroutechoicebehavior[J].GamesandEconomicBehavior, 2007, 58 (2): 394-406. [13]RoughgardenT.Selfishroutingandthepriceofanarchy[M].Cambridge:MITPress, 2005. [14]BeckmannMJ,MeguireCR,WinstenCB.Studiesintheeconomicsoftransportation[M].NewHaven:YaleUniversityPress, 1956. [15]FrankM,WolfeP.Analgorithmforquadraticprogramming[J].NavalResearchLogisticsQuarterly, 1956, 3 (1-2): 95-110. [16] 张欢, 卢毅, 朱东铁. 基于用户均衡分析的公路超限车辆补偿费率优化模型 [J]. 铁道科学与工程学报, 2012, 9 (6): 84-89. ZHANGHuan,LUYi,ZHUDongtie.Optimizationmodelonhighwayreimbursementrateofoversizevehicleswithuserequilibriumanalysis[J].JournalofRailwayScienceandEngineering, 2012, 9 (6): 84-89. [17] 史峰, 王英姿, 徐光明, 等. 考虑支路路段双向车流相互影响的单向交通组织优化 [J]. 铁道科学与工程学报, 2012, 9(2): 66-71. SHIFeng,WANGYingzi,XUGuangming,etal.Optimizationapproachforone-waytrafficorganizationwithbidirectionalflow’seffectoflocalroad[J].JournalofRailwayScienceandEngineering, 2012, 9(2): 66-71. [18] 周和平, 胡列格, 晏克非. 基于模糊路段流量的OD反推的不确定规划模型与算法研究[J]. 铁道科学与工程学报, 2005, 43(1):68-74. ZHOUHeping,HULieke,YANGKefei.Uncertainprogrammingmodelandalgorithmforestimatingorigin-destinationmatricesbasedonfuzzylinkflow[J].JournalofRailwayScienceandEngineering, 2005, 43 (1): 68-74. [19]WilliamAM,NancyAM.Travelestimationtechniquesforurbanplanning(NCHRPReport365) [M].Wasington,DC:NationalAcademyPress, 1998. [20] 胡列格, 夏云, 王佳, 等. 城市公共自行车高峰期需求不均衡的调度优化研究 [J]. 铁道科学与工程学报, 2015, 12(2): 441-448. HULiege,XIAYun,WANGJia,etal.Schedulingoptimizationresearchondemandimbalanceofurbanpublicbicyclesduringpeakperiod. [J].JournalofRailwayScienceandEngineering, 2015, 12(2): 441-448. [21] 童晓进, 符卓, 刘勇, 等. 连续消耗应急物资调运问题研究 [J]. 铁道科学与工程学报, 2013, 10 (5): 78-82. TONGXiaojin,FUZhuo,LIUYong,etal.Studyofemergencymaterialdispatchofthecontinuousconsumption[J].JournalofRailwayScienceandEngineering, 2013, 10 (5): 78-82. [22]Navteqoffciolwelsike[DB/OL].http://www.navteq.com/, 2016.7.4. [23]UScensusbareat[DB/OL].http://www.census.gov/geo/www/tiger/tgrshp2010/tgrshp20 10.html, 2016.7.4. Locating and researching of inefficient road clusters in a large-scale transportation network SUN Li, LING Ximan, TAN Qian, WANG Pu (SchoolofTrafficandTransportationEngineering,CentralSouthUniversity,Changsha410000,China) Inthispaper,roadandclusterofroadsintransportationnetworkwereclassifiedasinefficientornecessaryaccordingtotheireffectontheefficiencyoftheroadnetwork,basedonBraess'sparadox.Reasonableclosureofinefficientlinkscanreducetravelcostsconsiderably,whilethefailureofnecessarylinkswouldresultinextratraveldelays.Wemodifiedtheadaptivegeneticalgorithmtopinpointinefficientroadclustersinareallarge-scaletrafficnetwork.Actualtransportationnetworkdatafromgeographicalinformationsystems(GIS)anddailycommutingorigindestinationmatrixintheSanFranciscowereused.Ourempiricalresultsshowthatinefficientroadclustersincludenotonlyinefficientroadbutalsonecessaryroad.Meanwhile,thedegreeofinefficiency|ΔTS|increasesfirstandthendecreasesasthenumberofroadsintheroadclustersincrease.Inefficientroadclusterscontainlessroadwithlarge|ΔTS|,whichismuchmorecommonaswell. efficiencyofurbantraffic;Braess’sparadox;largescaletransportationnetwork;adaptivegeneticalgorithm 2015-11-15 中央高校基本科研业务费专项资金资助项目(2015zzts207) 王璞(1983-),男,河北石家庄人,教授,博士,从事交通运输规划与管理、统计物理学、复杂网络和数据挖掘方面的研究;E-mail:wangpu@csu.edu.cn U491.1+3 A 1672-7029(2016)07-1414-063 旧金山市道路网络实证分析
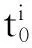

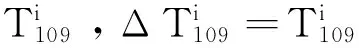


4 结论
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

