荷载横向变位下的单箱双室剪力滞效应研究

张玉元，张慧，张元海，杨娟

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.甘肃省陇南公路管理局，甘肃 陇南 746000)



荷载横向变位下的单箱双室剪力滞效应研究

张玉元1，张慧1，张元海1，杨娟2

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.甘肃省陇南公路管理局，甘肃 陇南 746000)

荷载横向对称变位时，箱梁顶板、底板纵向位移存在差异，因此顶板、底板采用不同的剪力滞广义位移，同时在计算外力势能时应考虑荷载横向位置的影响，选取余弦函数为剪力滞翘曲位移函数，利用能量变分原理推导出荷载横向变位下的箱梁截面控制微分方程，结合边界条件给出均布荷载下箱梁顶板、底板的纵向应力解。选择一典型的单箱双室简支箱梁，分析跨中截面顶板、底板的剪力滞横向分布规律，高跨比对跨中截面关键点剪力滞系数的影响规律，研究表明：荷载由边腹板对称向单室顶板中心移动时，顶板与腹板交汇处剪力滞系数将由正剪力滞变为无剪力滞，再由无剪力滞变为负剪力滞，但是对底板的剪力滞效应的影响几乎很小，底板与腹板交汇处剪力滞系数基本保持正剪力滞；荷载不同的横向变位下，高跨比对剪力滞效应的影响各不相同，因此在多箱室设计中应充分考虑荷载变位的影响。此外本文计算结果与有限元数值解吻合良好，能够正确的反映剪力滞规律。

单箱双室；剪力滞效应；能量变分法；荷载位置；有限元

本文研究箱梁的剪力滞效应不同于以往将荷均匀对称的施加在腹板处，忽略了荷载在顶板上横向对称移动时，顶板、底板截面的剪力滞效应规律。蔺鹏臻等[1]选取一典型的单箱双室简支箱梁，腹板处施加荷载的分配方式上有了改变，但是并没有考虑荷载的横向移动；李新平等[2-4]针对单箱双室简支箱梁的剪力滞效应研究，也未涉及到荷载横向移动的问题；吴亚平等[5]选取二次抛物线为剪力滞翘曲位移函数，考虑了荷载在横向变位，利用能量变分法研究了单室简支箱梁顶板、底板的剪力滞效应；白玉堂等[6]选取三次抛物线为剪力滞翘曲位移函数，分别对悬臂板、顶板、底板选用不同的剪力滞广义位移，采用能量变分研究了单室箱梁各个翼板的横向剪力滞规律。本文选取余弦函数为剪力滞翘曲位移函数，考虑顶板、底板采用不同的剪力滞广义位移U，针对荷载在横向对称移动时，利用能量变分原理推导出横向变位下箱梁截面的控制微分方程，并结合边界条件给出均布荷载下顶板、底板的纵向应力解，分析箱梁截面测点的横向剪力滞规律和高跨比对测点剪力滞系数的影响规律；同时利用ANSYS中的Solid45单元建立箱梁有限元模型分析荷载横向变位下的剪力滞效应并获得测点的数值解，对比本文解析解和数值解，发现吻合程度良好，能够正确的反映剪力滞规律。

1　剪力滞效应截面控制微分方程的推导

考虑荷载横向作用在箱梁顶板对称的任意位置η处时顶板、底板具有不同的翘曲程度，对顶板、底板采用不同的最大剪切转角差U1和U2。箱梁截面及坐标系如图1所示，箱梁在竖向任意荷载q(z)作用下的挠曲变形，则箱梁截面任意一点处的纵向位移u(x,y,z)为：

u(x,y,z)=-y·w′(z)+ωζ(x,y)·U(z)

(1)

式中：w(z)为竖向挠度；ωζ(x,y)为翘曲位移函数；U(z)为剪切变形最大差值；式中第一项为初等梁纵向位移，第二项为剪力滞引起的附加位移。

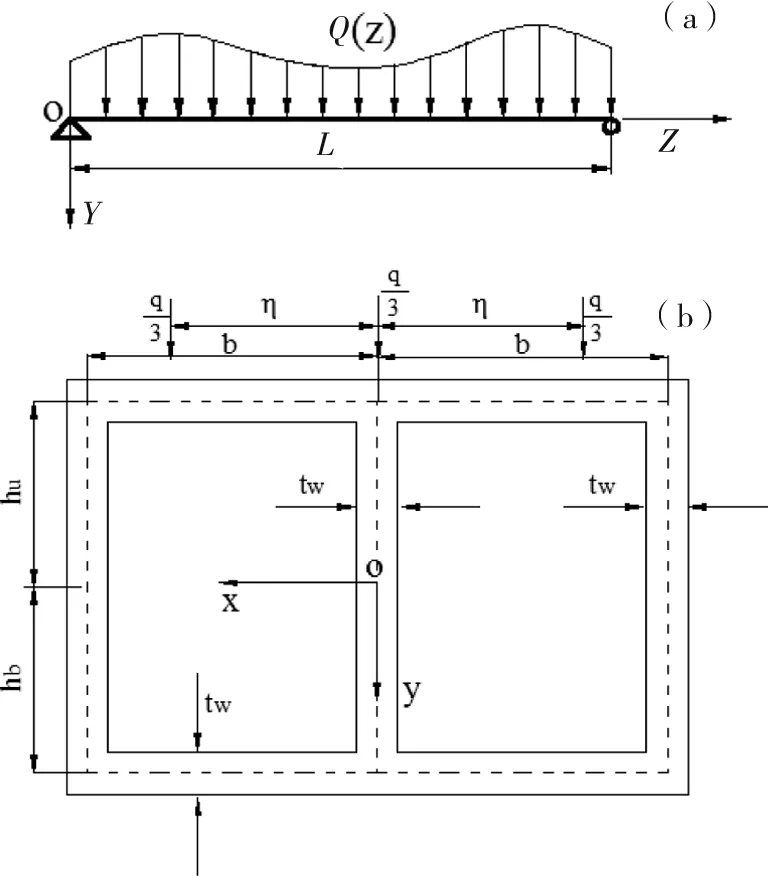
(a)坐标系及荷载;(b)横截面图1　箱型截面简图Fig.1 Box girder with cross section

式(1)中的剪力滞翘曲位移函数取：

(2)

将式(2)代入式(1)可得顶板、底板的纵向位移表达式：

顶板：

(3)

底板：

(4)

假设变形后横截面与中性轴垂直，顶板、底板的竖向位移ω1(x,z,η)、ω2(x,z,η)和纵向位移的关系式如下：

(5)

(6)

将式(5)和(6)积分，得出竖向位移ω(x,z,η)在横向也是余弦函数分布。

(7)

(8)

当荷载作用在η=b时，有ω1(x,z,η)=ω2(x,z,η)=ω(z,η)，则式(7)和(8)中的C1=C2=0，则式(7)和(8)可写为

ω1(x,z,η)=ω(z,η)+

(9)

ω2(x,z,η)=ω(z,η)+

(10)

当荷载q(z)作用于顶板x=η处时，外力势能的表达式为

(11)

顶板、底板应变能表达式：

(12)

(13)

式(12)和(13)中：

腹板应变能：

(14)

箱梁总势能：

π=U1+U2+Uω+V

(15)

式(15)中：I1,I2和Iω分别为顶板、底板、悬臂板惯性矩；E为弹性模量；G为剪切模量；M(z)和Q(z)分别为箱梁某一截面的弯矩和剪力。

将式(15)求一阶变分，并令δπ=0

δU1dz

(16)

根据变分引理，由(16)式可得截面控制微分方程

(17)

(18)

(19)

(20)

(21)

式(18)-(19)整理得

(22)

联立式(17)、(18)和(22)可得

(23)

由弹性力学可知顶板、底板纵向应力解分别为

(24)

(25)

(26)

2　简支梁受均布荷载横向变位时顶板、底板纵向应力的解答

(27)

(28)

(29)

将式(28)代入式(23)可得

(30)

式(30)的解为

(31)

(32)

(33)

将式(32)和(33)分别代入式(24)和(25)，可得到顶板、底板的纵向应力解，进而求得截面各个测点的剪力滞系数。

3　算例分析

本文基于一典型的无悬臂板单箱双室简支箱梁为例，在均布荷载下，分析图2中3种变位下跨中截面顶板、底板各个测点的剪力滞系数横向变化规律，采用ANSYS中的Solid45单元建立有限元模型，对比分析本文理论的正确性和合理性；分析了跨中截面关键测点剪力滞系数随高跨比的变化规律。

(a)变位1(腹板处)；(b)变位2(单室顶板中心)(c)变位3(中腹板)图2　荷载横向变位图Fig.2 load lateral moving

3.1单箱双室简支箱梁算例概况

跨度3m的简支混凝土单箱双室箱梁为例,截面尺寸、测点位置见图3，材料E=3.15×104Mpa，泊松比μ=0.3，满跨均布线荷载q/3=600N/m；箱梁有限元模型如图(4)；对于本算例中广义位移U的一阶导数值如表1。

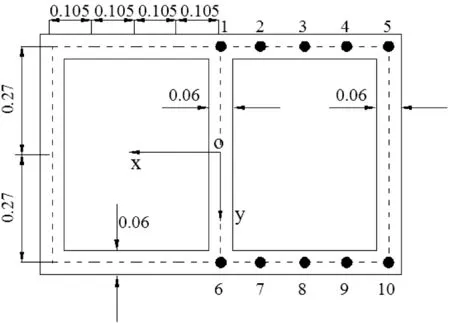
单位：m图3　截面尺寸及测点Fig.3 Cross section size

3.2工况分析

3.2.1跨中截面剪力滞系数横向分布规律

选取跨中截面，分别计算荷载横向变位时3种工况的截面测点剪力滞系数，并绘制剪力滞系数横向分布规律曲线，通过Solid45单元分析截面测点纵向应力解，并计算剪力滞系数绘制横向分布曲线；如图5、6、7。

图4　ANSYS有限元模型Fig.4 ANSYS finite element model

Table1Firstorderderivativeofgeneralizeddisplacementinthisexample

荷载位置翼板变位1、变位3变位2U'11.186×10-7-3.33×10-7U'21.186×10-71.176×10-7

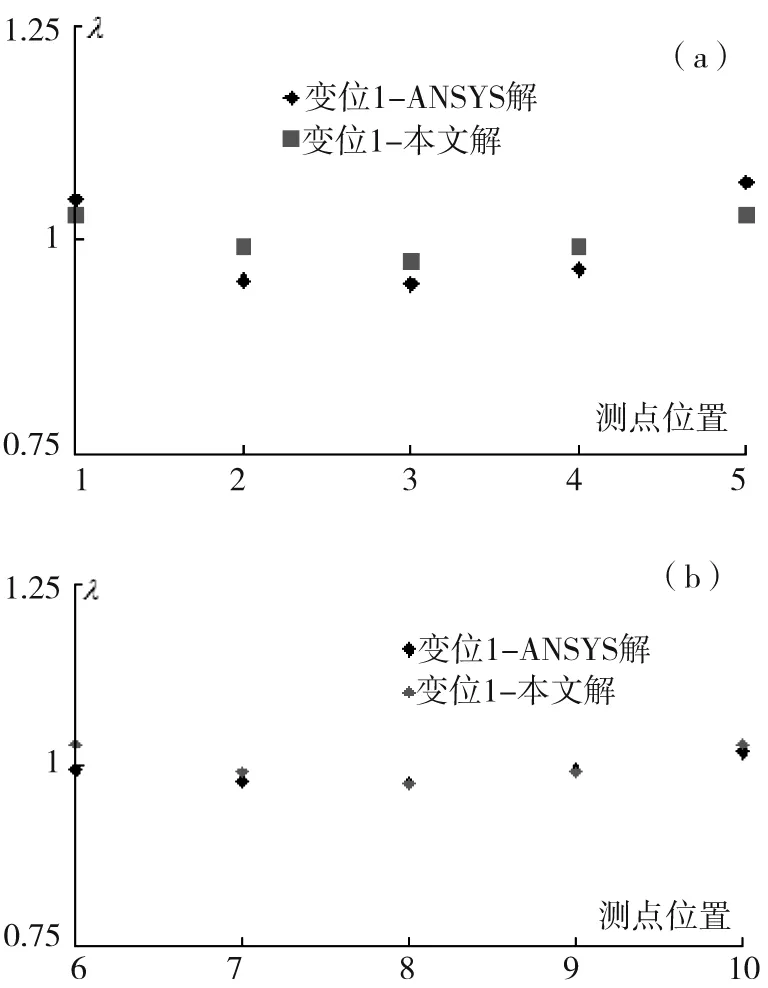
(a)顶板各个测点剪力滞系数横向分布规律(b)底板各个测点剪力滞系数横向分布规律图5　变位1-跨中截面剪力滞系数横向分布规律Fig.5 Load location 1-lateral distributive law of shear lag coefficient in the mid-span cross section

(a)顶板各个测点剪力滞系数横向分布规律(b)底板各个测点剪力滞系数横向分布规律图6　变位2-跨中截面剪力滞系数横向分布规律Fig.6 Load location 2-lateral distributive law of shear lag coefficient in the mid-span cross section

(a)顶板各个测点剪力滞系数横向分布规律 (b)底板各个测点剪力滞系数横向分布规律图7　变位3-跨中截面剪力滞系数横向分布规律Fig.7 Load location 3-lateral distributive law of shear lag coefficient in the mid-span cross section

3.2.2高跨比对跨中截面测点剪力滞效应的影响

高跨比(H/L)是影响剪力滞效应较为敏感的因素之一[7]，通过调整图3箱梁截面的高跨比，利用本文解析解研究跨中截面顶板1号、3号测点和底板6号、8号测点剪力滞系数随高跨比的变化规律，并绘制变化曲线；如图8和9所示。

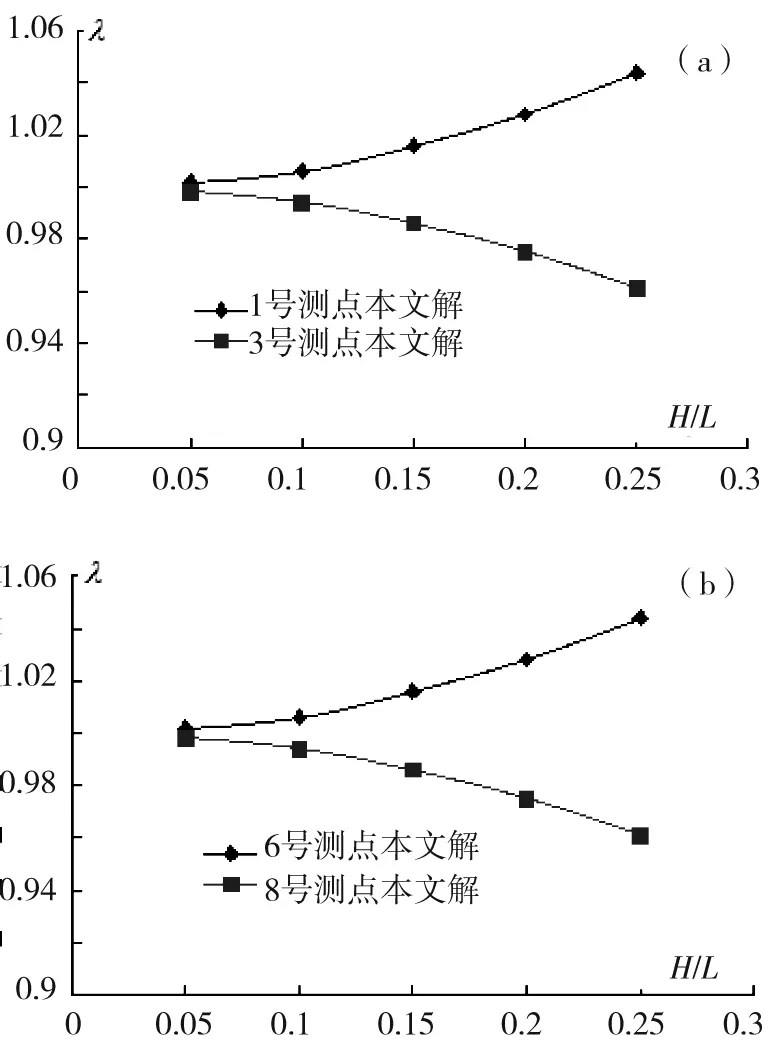
(a)顶板测点剪力滞系数随高跨比的变化规律(b)底板测点剪力滞系数随高跨比的变化规律图8　变位1、变位3-跨中截面测点剪力滞系数随高跨比的变化规律Fig.8 Load location 1 and 3-shear lag coefficient changing with the height-span ratio in the mid-span cross section

3.3结果分析

3.3.1跨中截面剪力滞横向变化规律

顶板：1)变位1、变位3时，跨中截面剪力滞变化规律为：由腹板向单室顶板中间递减；

2)变位2时，跨中截面剪力滞变化规律为：由腹板向单室顶板中间递增；

3)变位1时，跨中截面5号测点的剪力滞系数比1号测点的剪力滞系数大一些；

4)变位2、变位3时，跨中截面1号测点的剪力滞系数比5号测点的剪力滞系数大一些；

5)荷载由边腹板向单室顶板中间移动时，1号、5号测点剪力滞系数由正剪力滞变为无剪力滞，再由无剪力滞变为负剪力滞。

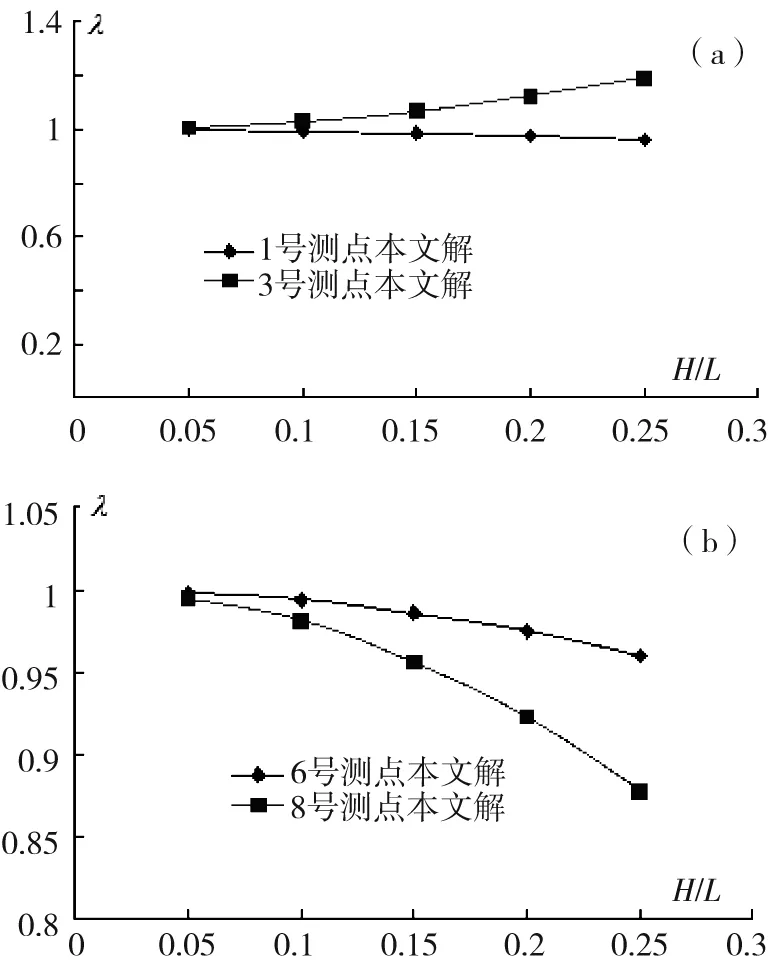
(a)顶板测点剪力滞系数随高跨比的变化规律(b)底板测点剪力滞系数随高跨比的变化规律图9　变位2-跨中截面测点剪力滞系数随高跨比的变化规律Fig.9 Load location 2-Shear lag coefficient changing with the height-span ratio in the mid-span cross section

底板：1)荷载在横向变位下，跨中截面底板的剪力滞影响几乎很小，依然是由腹板向单室底板中间递减；

2)变位2、变位3时，跨中截面6号测点剪力滞系数比10号测点剪力滞系数大一些。

3.3.2关键点跨中截面剪力滞系数随高跨比增大的变化规律

1)变位1、变位3∶1号和6号测点跨中截面剪力滞系数随高跨比的增大而增大；3号和8号测点跨中截面剪力滞系数随高跨比的增大而减小。

2)变位2：1号测点跨中截面剪力滞系数随高跨比的增大而增大；3号、6号和8号测点跨中截面剪力滞系数随高跨比的增大而减小。

4　结论

1)荷载由边腹板对称向单室顶板中心移动时，顶板与腹板交汇处剪力滞系数将由正剪力滞变为无剪力滞，再由无剪力滞变为负剪力滞，但是顶板荷载的横向变位并没有破坏底板剪力滞横向分布规律，此外，底板与腹板交汇处剪力滞系数基本保持正剪力滞。

2)跨中截面剪力滞横向分布规律为：边荷载分别作用在边腹板上和边荷载都移动到中腹板时，顶板剪力滞系数由单室中心向两侧腹板递增，底板规律也是如此；边荷载作用在单室顶板中心时，顶板剪力滞系数由单室中心向两侧腹板递减，底板剪力滞系数由单室中心向两侧腹板递增。

3)高跨比对跨中截面剪力滞系数的影响规律：边荷载分别作用在边腹板上和边荷载都移动到中腹板时，跨中截面中腹板处剪力滞系数随高跨比的增大而增大，跨中截面单室顶板、底板中心处剪力滞系数随高跨比的增大而减小；边荷载作用在单室顶板中心时，跨中截面单室顶板中心处的剪力滞系数随高跨比的增大而增大，中腹板处、单室底板中心处剪力滞系数随高跨比的增大而减小。

4)研究荷载横向变位下的箱梁顶板、底板的剪力滞效应，考虑到箱梁在竖向对称荷载下顶板、底板具有不同的翘曲程度，因此顶板和底板采用不同的剪力滞广义位移，利用能量变分原理推导出箱梁在横向对称荷载变位时截面控制微分方程，结合边界条件给出均布力下的纵向应力解，并通过ANSYS有限元解与本文解析解对比发现，吻合程度良好，能够精确的反映剪力滞规律，验证了本文理论的正确性。

[1] 蔺鹏臻，孙理想，扬子江，等.单箱双室简支箱梁的剪力滞效应研究[J].铁道工程学报，2014，1(1)：59-63.

LINPeangzhen,SUNLixiang,YANGZijiang,etal.Researchonshearlageffectoftwin-cellboxgirders[J].JournalofRailwayEngineering，2014，1(1)：59-63.

[2] 李新平，曾永雄.单箱双室箱梁剪力滞效应的分析[J].低温建筑技术，2015，1(1)：64-65.

LIXinping,ZENGYongxiong.Analysesofshearlageffectoftwin-cellboxgirders[J].LowTemperatureConstructionTechnology，2015，1(1)：64-65.

[3] 刘勇，张丽，张元海，等.单箱双室剪力滞效应的差分解[J].兰州交通大学学报，2012，31(3)：31-34.

LIUYong,ZHANGLi,ZHANGYuanhai,etal.Differencesolutionforshearlageffectoftwin-cellboxgirder[J].JournalofLanZhouJiaoTongUniversity，2012，31(3)：31-34.

[4] 雒敏，蔺鹏臻，孙理想.单箱双室箱梁的剪力滞效应分析[J].力学与实践，2013，35(6):70-74.LUOMin,LINPengzhen,SUNLixiang.Analysisofshearlageffectoftwin-cellboxgirders[J].JournalofMechanicsandPractice,2013,35(6):70-74.

[5] 吴亚平，杨玫，周大为，等.荷载横向变位下箱梁顶板与顶板的剪力滞效应分析[J].土木工程学报，2007，40(10)：8-12.

WUYaping,YANGMei,ZHOUDawei,etal.Analysesoftheshearlageffectonthetopandbottomplatesofboxbeamswithvaringloadinglocations[J].JournalofCivilEngineering，2007，40(10)：8-12.

[6] 白玉堂，任建新.考虑荷载横向变位时箱梁剪力滞效应的解析解[J].铁道科学与工程学报，2015，12(2)：347-353.

BAIYutang,RENXinjian.Ananalyticsolutiontoshearlageffectsoftheboxgirderwithrespecttovaryinglateralloadingpositions[J].JournalofRailwayScienceandEngineering，2015，12(2)：347-353.

[7] 郭金琼，房贞政，郑振.箱型设计理论[M].第二版北京：人民交通出版社，2008.

GUOJinqiong,FANGZhenzheng,ZHENGZhen.Designtheoryofboxgirder[M]. 2ndeditionBeijing:ChinacommunicationsPress,2008.

Research on shear lag effect of twin-cell box girderswith varying loading locations

ZHANG Yuyuan1,ZHANG Hui1，ZHANG Yuanhai1,YANG Juan2

(1.SchoolofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China；2.LongnanHighwayAdministrationBartanofGansuProrince,Longnan746000,China)

Thelongitudinaldisplacementofboxgirder’sthetopandbottomplatesaredifferenceswiththeloadinglateralsymmetrymoving,Therefore,differenttheshearlaggeneralizeddisplacementwererespectivelyusedforthetopandbottomplates,thepotentialenergyofexternalforcewascalculatedbyconsideringtheinfluenceoflateralloadingpositions,selectingcosinefunctionfortheshearlagwarpingdisplacementfunction,byusingtheenergyvariationalmethodtodeducetheboxgirdercrosssectioncontroldifferentialequationswiththeloadinglateralsymmetrymoving,combiningwiththeboundaryconditionsofboxgirderunderuniformlydistributedloadaregivenlongitudinalstresssolutionofthetopandbottomplates.Tochooseatypicaltwin-cellsimplysupportedboxgirder,analysisofthelawsoftheshearlaglateraldistributioninthemid-spansectionofthetopandbottomplatesandtheheight-spanratioinfluencedthechangingofshearlageffectcoefficientofkeypointsinthemid-spansection,researchshows:withthesymmetricalloadingonthetopplatemovingfromsidewebstothecenterofsingleroom,theshearlageffectonthetopplatenearthewebschangefrompositivetonegative,andtheshearlageffectonthebottomplatenearthewebsrarelychangesbasicallyremainpositive;designingofmulti-cellboxgirder,theinfluenceofdifferentloadpatternsofshearlageffectshouldbeconsideredfully.Theresultsareingoodagreementwiththosefromfiniteelementmethodandaccuratelyreflectthelawofshear-lag.

twin-cellboxgirders;shearlageffect;energyvariationalmethod;loadlocation;finiteelement

2015-11-15

国家自然科学基金资助项目(51508255,514680325,51268029)；教育部“长江学者和创新团队发展计划”资助项目(IRT1139)；2015人社部留学人员科技活动资助项目

张元海(1965-)，男，甘肃武山人，教授，博士，从事箱型号梁设计理论研究；E-mail:2yh17012@163.com

U441+.5

A

1672-7029(2016)07-1309-08