改进的粒子滤波算法及其在车牌跟踪中的应用
肖宇麒,潘迪夫,韩锟
(中南大学 交通运输工程学院,湖南 长沙 410075)

改进的粒子滤波算法及其在车牌跟踪中的应用
肖宇麒,潘迪夫,韩锟
(中南大学 交通运输工程学院,湖南 长沙 410075)
针对粒子滤波算法精度、效率不高及样本贫化等问题,提出通过量子粒子群算法和自适应遗传算法改进的粒子滤波算法。在粒子滤波重采样之后,考虑采用量子粒子群算法的位置更新方程对粒子分布进行改善;再按适应度大小对样本排序,滤除适应度值低于平均水平的粒子,选取相应数量较优粒子替换被滤除粒子。为保证样本多样性和有效粒子数量,引入自适应遗传算法对粒子进行交叉、变异操作。选择非线性目标跟踪模型和分时恒定值模型对本文改进算法进行仿真,仿真结果表明本文算法精度、数值稳定性均高于同类算法;最后将本文算法运用于汽车视频跟踪实验中,实验结果表明本文算法对目标跟踪中物体快速运动、光线和背景剧烈变化的情况都有准确的跟踪效果。
粒子滤波;车牌跟踪;量子粒子群算法;自适应遗传算法
快速移动的机动目标跟踪属于典型的信息融合应用领域,它对精度和实时性要求高,具且有非线性、非高斯的特点[1]。在导航、监控、风速预测、图像识别和目标跟踪中都有着广泛应用,也一直是研究的热点和难点。粒子滤波作为一种后验概率的求解方法,通过非参数化的蒙特卡洛模拟方法实现递推贝叶斯滤波[2],精度逼近最优估计,适用于处理用状态空间表示的非线性、非高斯时变系统的状态滤波及参数估计等问题,在目标跟踪领域应用前景广阔[3]。但是传统粒子滤波方法(简称PF算法)仍存在一些不足,比如粒子样本贫化,PF算法通过重采样复制权重较大粒子来替换迭代过程中产生粒子退化的大部分权重较小的粒子,导致粒子样本多样性损失[4]。此外PF算法因为采用粒子集表示概率需要大量粒子集,并且伴随不断的重采样淘汰大量无效粒子的过程,故计算效率较低[5]。
为解决PF算法存在的这些问题,国内外学者提出了很多改进办法,张光等[6]通过正则化粒子滤波方法解决粒子贫化问题,但其对非线性系统参数估计误差偏大。常天庆等[7]按局部重采样算法对粒子分类,对权值过大、过小的粒子进行随机线性组合,一定程度解决了粒子集样本贫化问题,但是降低了PF算法计算效率,且对算法精度没有明显改善。Kao等[8-9]将GA算法运用在PF算法重采样之后,通过交叉变异更新粒子,用于缓解样本退化,一定程度提高了PF算法精度,但是使得PF算法计算效率更低。陈志敏等[10-11]把PSO算法引入PF算法,加速粒子向全局最优位置收敛,一定程度提高了PF算法计算效率,但是计算精度较低,且没有解决粒子集样本贫化的问题。这些算法虽然在一定程度上解决了传统PF算法存在的问题,但是都没有兼顾算法收敛速度、计算精度和粒子样本多样性。
因此,本文将基于波函数的量子粒子群算法(简称QPSO算法)和基于种群收敛分析的自适应遗传算法(简称AGA算法)有序结合,提出了QPSO-AGA-PF算法,该算法综合了QPSO算法的局部搜索能力和计算效率、AGA算法的全局搜索能力以及PF算法的非线性滤波原理,通过非线性目标跟踪模型和分时恒定值模型的仿真及高速公路车辆车牌跟踪实验表明该算法精度大、数值稳定性高,在物体快速运动、光线和背景剧烈变化等情况下都能够完成对目标车辆车牌的精确跟踪。

1 QPSO、AGA和标准PF算法
1.1QPSO算法
相对于PSO算法,QPSO算法无需粒子速度信息,控制参数少,运算过程更简单,故收敛效率高[12]。在QPSO系统中,粒子状态由波函数ψ(X,t)确定;波函数模的平方|ψ|2是粒子位置的概率密度函数,记为Q,QPSO算法表达式为:
(1)
式中:Mj(t)为所有粒子自身最优位置的平均;S为种群规模大小;Pij为第i个粒子自身最优位置的j维分量。粒子的位置更新方程为:
(2)
α是压缩扩张因子,可调节粒子收敛速度,孙俊等人已证明当α<1.78时算法收敛[13]。粒子当前最优位置Pi和种群最优位置Pg的更新方式为:
(3)
1.2AGA算法
在这里计算fmax与f的差值,而非fmax与ft的差值,目的是滤除适应度低于平均适应度的较差个体,更准确反应种群个体过早收敛程度。AGA算法具体表达式为:
(4)
传统GA算法中交叉和变异概率等控制参数与种群进化过程无关,这种固定不变的控制参数机制容易导致过早收敛[14]。而AGA算法的交叉概率Pg、变异概率Pm在种群迭代进化过程中根据种群收敛程度Δ进行自适应调整。
1.3标准PF算法
PF算法基本思想是构造一个基于随机样本及其权重的后验概率密度函数,将积分运算变为有限样本点的求和运算[15]。系统的动态空间模型表示如下:
(5)
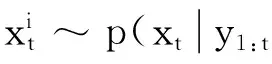
根据贝叶斯准则,推导迭代过程权值更新公式为:
(6)
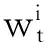
(7)
为时刻t粒子i的权重值。t时刻粒子后验概率密度为:
(8)
其中δ为狄拉克函数。
2 QPSO-AGA-PF跟踪算法
2.1QPSO-AGA-PF算法原理
QPSO算法相比于GA算法操作简单,收敛速度快、计算效率高,且其寻找最优解过程依据的是个体历史信息以及当前最优解同个体距离大小调整个体位置更新幅度与方向,能避免盲目搜索,在对以往搜索经验的学习利用上优于GA算法;但因为QPSO算法在迭代过程若发现一个当前最优解则其它粒子会向其聚拢且聚集至改最优解因此容易造成种群多样性丧失,又因为群体个体缺乏相互作用,无遗传机制,故群体可能早熟于局部最优解。GA算法采用竞争机制,通过交叉、变异操作选来选择进入下一次迭代的最优解,整个种群均匀地向全局最优解移动,相比QPSO算法有更强的全局搜索能力,且其遗传操作保证了种群的多样性;但其交叉、变异操作随机变动,搜索过程具有盲目性,故计算效率低。
考虑到QPSO算法计算效率及全局搜索能力虽优于标准PSO算法,但仍存在趋于早熟、样本多样性损失、精度低的问题;而AGA算法虽然提高了传统GA算法精度,但仍存在局部寻优能力差、计算效率低的不足。因此本文将QPSO算法较好的局部搜索能力、计算效率与AGA算法较强的全局寻优能力结合,提出基于量子粒子群算法与自适应遗传算法的改进粒子滤波算法,简称QPSO-AGA-PF算法。
QPSO-AGA-PF算法是指在PF算法重采样之后通过QPSO算法的位置更新方程改善粒子分布,位置更新之后,按适应度大小对样本排序,舍弃适应度低于平均水平的较差粒子,再从较优粒子中随机选取相应数量粒子按公式(4)进行交叉、变异并替代较差粒子。如此则既可极大地丰富样本多样性,又能提高算法计算效率与精度。
2.2目标模型
目标模型初始状态定义为X=[x,x′,y,y′],其中(x,y)表示模板位置,(x′,y′)表示x、y方向的速度,系统状态模型为:
Xt=AXt-1+Bwt-1
(9)
其中:A为系统状态转移矩阵,wt-1为满足标准正态分布的随机噪声。
设目标模型颜色直方图为p,粒子所在区域颜色直方图为q,则由Bhattacharyya系数来衡量的相似度ρ(p,q)、距离d表示如下:
(10)
(11)
观测概率密度函数(似然函数)表示如下:
(12)
其中:σc为常数,本文定义该似然函数为粒子的适应度函数,即t时刻i粒子的适应度值为:
(13)
(14)
2.3QPSO-AGA-PF跟踪算法流程
以下是QPSO-AGA-PF算法具体描述:
1)初始化采样:
令t=0,在初始帧手动选取参考目标X,以此时

2)重要密度采样:
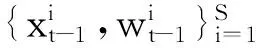

c)更新:按照公式(7)、(8)更新权重值、概率密度;
3)粒子退化程度判断:
(15)
根据公式(15)判断粒子退化程度,若有效粒子
数Neff小于规定阈值Nth,表示退化严重,则进行重采样,否则跳过重采样,进入QPSO更新;
4)重采样:
选择复制较优粒子填补被滤除粒子的空档,保证有效粒子数目,避免粒子退化;
5)QPSO更新粒子:
通过QPSO算法的位置更新公式(2),加快寻优
进程,以提高跟踪效率;根据公式(13)计算QPSO更新后各个粒子的适应度值,保留适应度大于平均适应度的M个个体,再从保留的较优粒子中随机选取(S-M)个粒子组成新样本集作为步骤6的初始样本集;
6)AGA进化过程:
按照式(4)对步骤5得到的样本集进行交叉、变异,以适当丰富样本多样性、避免早熟;
7)权值更新及归一化处理并判断是否满足迭代终止条件,不满足则返回步骤2),否则迭代结束并输出t时刻目标的位置:
(16)
下面给出QPSO-AGA-PF跟踪算法流程图:
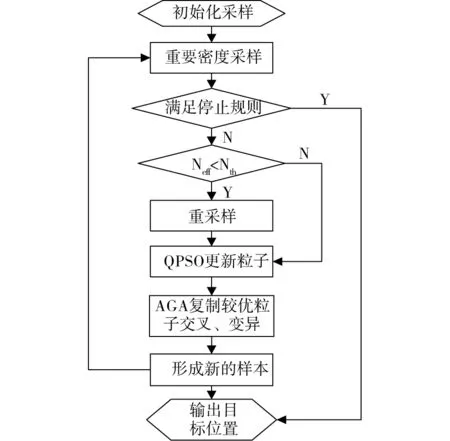
图1 QPSO-AGA-PF跟踪算法流程图Fig.1 Algorithm flowchart of QPSO-AGA-PF
3 目标模型仿真
为测试QPSO-AGA-PF跟踪算法性能,对粒子群算法改进的粒子滤波算法(简称PSO-PF)、遗传算法改进的粒子滤波算法(简称GA-PF)及本文算法进行仿真对比,3种算法分别通过非线性目标跟踪模型与分时恒定值模型两类目标模型进行了仿真测试。
3.1非线性目标跟踪模型
下面对一个强非线性、非高斯的目标跟踪问题进行仿真,系统的状态方程和观测方程为:
(17)
其中,过程噪声ut和观测噪声vt的均值设为0,方差分别设为1.5和0.05,均为高斯噪声,粒子数取100。
输出结果用各粒子滤波算法粒子集的均值表示:
(18)
一次独立实验的均方误差为:
(19)
3种算法的仿真测试结果如图2~图4所示:

图2 PSO-PF算法仿真测试结果Fig.2 Simulation results of PSO-PF
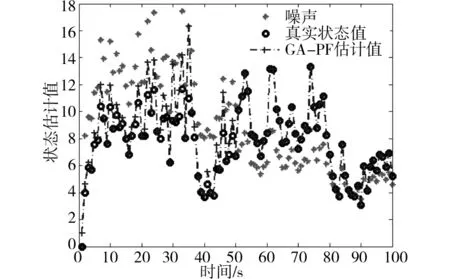
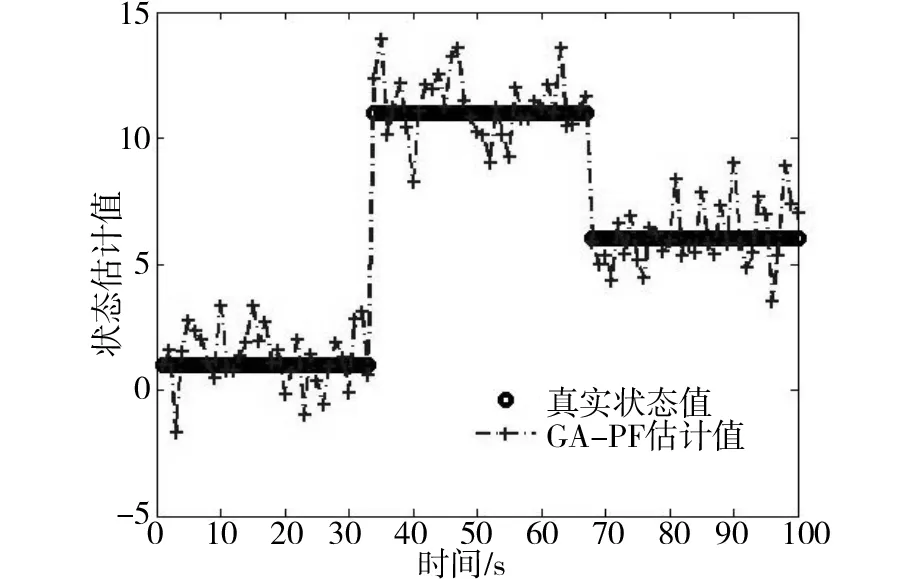
图3 GA-PF算法仿真测试结果Fig.3 Simulation results of GA-PF
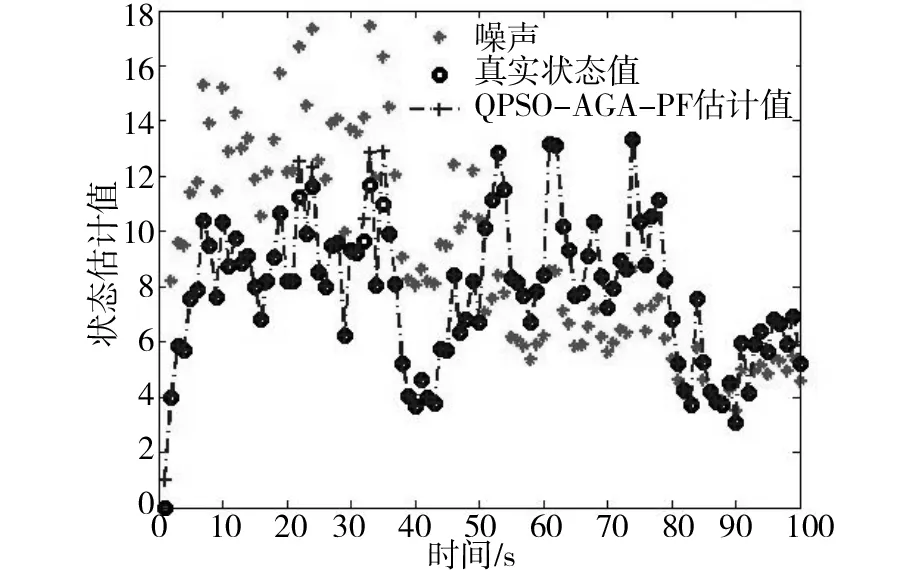
图4 QPSO-AGA-PF算法仿真测试结果Fig.4 Simulation results of QPSO-AGA-PF
50次独立实验均方根误差均值曲线如图5所示:
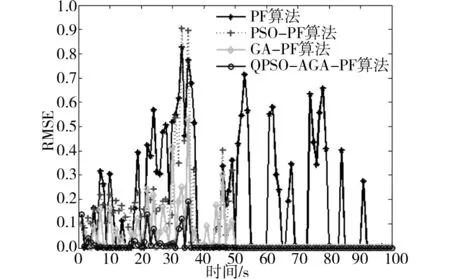
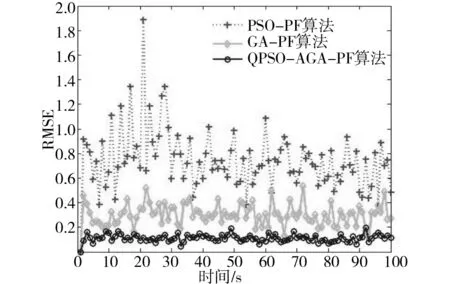
图5 各种算法多次运行RMSE均值曲线Fig.5 Average curve of RMSE after numbers of tests
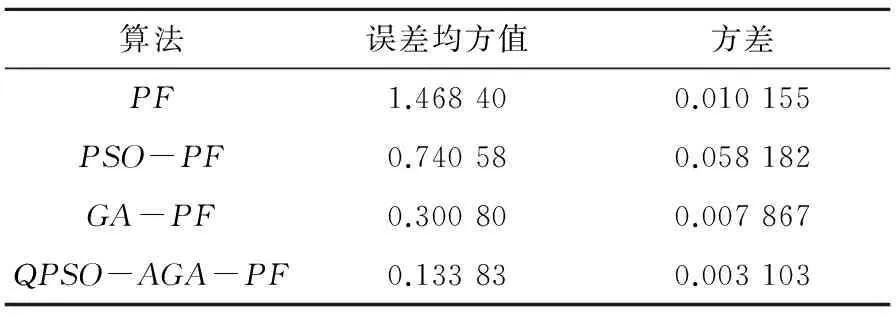
误差均方值及其方差统计如表1所示:
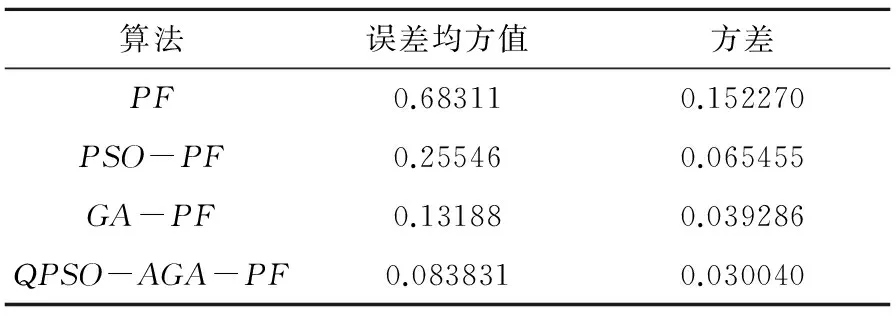
表1 各粒子滤波算法的误差均方值及其方差
由图2-图4可知,在50 由图5和表1可以看出PSO-PF算法和GA-PF算法相比于PF算法有很大改进,但是均方根误差最低都有0.131 88,而本文提出的QPSO-AGA-PF算法均方根误差仅为0.083 831,误差小了一个数量级,且均方根误差方差也是最小,对状态的估计精度最高,且具有更高的滤数值稳定性。 3.2分时恒定值模型 传统PF算法因样本贫化,跟踪估计能力不足,尤其在分时恒定值模型中表现明显,下面在分时恒定值模型中对各改进的粒子滤波算法仿真以测试其跟踪能力。 分时恒定模型的系统状态方程和观测方程如公式(20)所示: (20) 输出结果与单次独立实验的均方误差计算参考式(18)和式(19)。 PSO-PF、GA-PF及QPSO-AGA-PF3种算法的仿真测试结果如图6~8所示: 图6 PSO-PF算法仿真测试结果Fig.6 Simulation results of PSO-PF 图7 GA-PF算法仿真测试结果Fig.7 Simulation results of GA-PF 图8 QPSO-AGA-PF算法仿真测试结果Fig.8 Simulation results of QPSO-AGA-PF 50次独立实验均方根误差均值曲线如图9所示: 图9 各种算法多次运行RMSE均值曲线Fig.9 Average curve of RMSE after numbers of tests 误差均方值及其方差统计如表2所示: 表2 各粒子滤波算法的误差均方值及其方差 由图5-7可以看出,在分时恒定值模型仿真实验中,PSO-PF算法的状态估计曲线较严重偏离了真实状态,GA-PF算法的状态估计曲线也一定程度在真实状态上下也产生了较大震荡,而QPSO-AGA-PF算法贴合真实状态,实现了稳定、准确的跟踪。 由图9、表2可知PSO-PF算法和GA-PF算法均方根误差较大,最低为0.308 0,而QPSO-AGA-PF算法均方根误差仅为0.133 83且其方差也是最小,因此对状态的估计精度更高,且数值稳定性最高。 在视频跟踪过程中,要实时跟踪任意快速移动的目标,极为苛求算法的识别精度与抗干扰性;特别在当目标背景环境及所处光照环境发生急剧变化的情况下,要保证跟踪精度更是难上加难。为检验本文算法在目标跟踪应用中实际效果,对高速公路上汽车车牌进行了跟踪实验。 跟踪过程描述:蓝色跟踪框的跟踪目标为黑色汽车尾部车牌,该汽车在高速公路上途经一座高架桥,在其驶入高架桥底前以及驶出桥底后车牌均处于强光环境下随汽车高速移动且伴随路面不平频繁出现颠簸、侧移,在汽车完全驶入桥底的瞬间车牌经历了由强光照环境快速转至阴暗环境的过程,在汽车完全驶出桥底的瞬间车牌经历了由阴暗环境快速转至强光照环境的过程,在汽车完全驶出桥底后车牌不仅处于强光环境、频繁颠簸、侧移而且周围景物颜色更趋复杂多变。具体跟踪效果如图10所示。 图10 QPSO-AGA-PF算法第68、135、186、189、207、232、236、263帧车牌跟踪实验结果Fig.10 License tracking results of the 68th、135th、186th、189th、207th、232th、236th and 263th frame 跟踪效果分析:由图10可知,小车在视频207所示有跟目标车牌相似目标出现的情况下、在由186帧所示强光环境进入189帧所示弱光环境的情况、在207帧所示弱光环境持续高速行驶的情况、在232帧所示弱光环境进入236帧所示强光环境的情况以及在263帧所示强光环境持续高速行驶且背景复杂多变情况下,蓝色矩形跟踪框都能紧密贴合被跟踪车牌,实验表明QPSO-AGA-PF算法成功地克服了光照、背景剧烈变化对跟踪造成的极大干扰,满足了目标跟踪对精度与抗干扰性的要求。 1)对QPSO-AGA-PF算法通过非线性目标跟踪模型以及分时恒定值模型进行了仿真,实验结果均方根误差分别是0.083 831和0.133 83,均方根误差的方差分别是0.030 040和0.003 103,实验结果表明本文算法精度、数值稳定性均高于同类滤波算法。 2)将QPSO-AGA-PF算法运用于汽车视频跟踪实验中,实验结果表明本文算法对目标跟踪中物体快速运动、光线和背景剧烈变化的情况都有良好跟踪效果。 仿真和实验表明,本文算法精度、数值稳定性均高于同类算法,且具备良好的跟踪效果。 [1]CarpenterJ,CliffordP,FernheadP.Animprovedparticlefilterfornonlinearproblems[R].Oxford:UniversityofOxford, 1997. [2] 萧德云,莫以为.基于混合系统状态估计的故障诊断[J].自动化学报.2004,30(6),980-985. XIAODeyun,MOYiwei.Hybridsystemmonitoringanddiagnosingbasedonparticlefilteralgorithm[J].ACTAAutomaticaSinica. 2004,30(6):980-985. [3]NummiaroK,Koller-MeierE,VanGoolL.Anadaptivecolor-basedparticlefilter[J].ImageandVisionComputer, 2003(21):99-110. [4]KotechaJH,DjuricPM.Gaussianparticlefiltering[J].IEEETrans.SignalProcess, 2003, 51(10): 2592-2601. [5]ThrunS,LangfordJ,VermaV.Risksensitiveparticlefiters[J].AdrancesinNearalInformationProcessingSystems, 2001, 22(3): 961-968. [6] 张光,张英堂,任国全,等. 基于正则化粒子滤波的磁梯度张量跟踪方法[J].探测与控制学报.2014(2):0050-0053. ZHANGGuang,ZHANGYingtang,RENGuoquan,etal.TrackingMethodofMagneticGradientTensorBasedonRPF[J].JournalofDetection&Control. 2014(02):0050-03. [7] 常天庆,李勇,刘忠仁,等.一种改进重采样的粒子滤波算法[J].计算机应用研究,2013,30(3): 748-750. CHANGTianqing,LIYong,LIUZhongren,etal.Particlefilteralgorithmbasedonimprovedresampling[J].ApplicationResearchofCompulters, 2013,30(3): 748-750. [8]KaoY,ZaharaE.A.Hybridgeneticalgorithmandparticleswarmoptimizationformultimodalfunctions[J].AppliedSoftComputing, 2008,8(2):849-857. [9] 席涛,张胜修,原魁,等. 基于遗传进化策略的粒子滤波视频目标跟踪[J].光电工程, 2009,36(3):0158-0162 XITao,ZHANGShengxiu,YUANKui,etal.Videoobjecttrackingbasedonparticlefitlterwithgeneticevolutionstrategy[J].Opto-ElectronicEngineering, 2009,36(3):0158-162. [10] 陈志敏,薄煜明,吴盘龙,等. 基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J]. 控制与决策, 2013(2):193-200. CHENZhimin,BOYuming,WUPanlong,etal.Novelparticlefilteralgorithmbasedonadaptiveparticleswarmoptimizationanditsapplicationtoradartargettracking[J].ControlandDecision, 2013(2):193-200. [11] 李明,逄博,年福忠. 基于混沌的PSO粒子滤波算法[J]. 计算机工程,2012(8): 0134-0137. LIMing,PANGBo,NIANFuzhong.Particleswarmoptimizationparticlefilteringalgorithmbasedonchaotic[J].ComputerEngineering, 2012(8): 0134—0137. [12] 孙俊. 量子行为粒子群优化算法研究[D].无锡:浙江大学,2009. SUNJun.Particleswarmoptimizationwithparticleshavingquantumbehavior.[D]Wuxi:ZhejiangUniversity,2009. [13]ParkS,HwangJ,RouetalK.Anewparticlefilterinspiredbybiologicalevolution:Geneticfilter[J].InternationalJournalofAppliedScienceEngineeringandTechnology, 2007, 4(1):459-463. [14]SrinivasM,PatnaikLM.Adaptiveprobabilitiesofcrossoverandmutationingeneticalgorithm[J].IEEETrans.OnSystems,ManandCybermetics,1994,24(4):656-667. [15]ParkSeongkeun,JaePilHwang,EuntaiKim,etal.Anewevolutionaryparticlefilterforthepreventionofsampleimpoverishment[J].IEEETransactionsonEvolutionaryComputation, 2009, 13(4):801-809. Improved particle filter algorithm and its application in target tracking XIAO Yuqi,PAN Difu,HAN Kun (SchoolofTraffic&Transportation,CentralSouthUniversity,Changsha410075,China) Tosolvetheproblemsoflowaccuracy,inefficiencyandsampleimpoverishmentofparticlefiltermethod,theimprovedmethodcombiningquantumparticleswarmoptimizationandadaptivegeneticalgorithmwasproposed.Afterre-sampling,theparticledistributionwasimprovedbythepositionrenewalequationofthequantumparticleswarmoptimization.Thenthesamplesweresortedaccordingtotheirfitness,andtheparticleswithfitnessvalueslessthanaveragefitnesswerefiltered.Thenoptimalsampleswereselectedtoreplacetheabandonedonesandcrossover,mutatewithadaptivegeneticalgorithm,soastoensurethesamplevalidityanddiversity.Themodifiedalgorithmwassimulatedinnonlineartargettrackingmodelandtime-constantvaluemodelandprovedtobehighinalgorithmaccuracyandnumericalvaluestability.Thismethodwasalsoappliedtothecartrackingexperimentandprovedtobeveryefficientandaccurateespeciallyundertheconditionthatthetargetmovedfastandtheintensityandbackgroundchangeddramatically. particlefilter;licenseplatetracking;quantumparticleswarmoptimization;adaptivegeneticalgorithm 2015-11-13 国家自然科学基金资助项目(U1334205) 潘迪夫(1957-),男,广东兴宁人,教授,从事称重调簧架车机研究;E-mail:difupan@csu.edu.cn TP391.41 A 1672-7029(2016)07-1393-08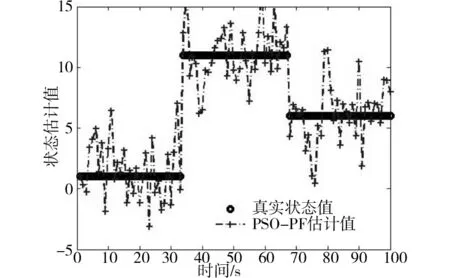

4 车牌跟踪实验

5 结论

