基于自适应多种群遗传算法的圆度误差评定*

刘思遥,黄美发,,冯建国,程彬彬,吴　芬,吴常林



基于自适应多种群遗传算法的圆度误差评定*

刘思遥1,黄美发1,2,冯建国2,程彬彬1,吴芬1,吴常林1

(1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.桂林机床股份有限公司，广西 桂林 541000)

针对传统遗传算法在圆度误差评定方法存在搜索稳定性差、易陷入局部收敛和全局搜索能力不足的问题，改进传统遗传算法(TGA)，提出了采用自适应多种群遗传算法(AMPGA)的评定方法。根据圆度误差评定的特点，建立了多种群协同进化的遗传方式，并引入了交叉概率Pc和变异概率Pm随个体适应度值变化而不断调整的遗传机制，通过编写自适应多种群遗传算法(AMPGA)程序对圆度误差进行评定，得到相应结果与三坐标测量机的实测值对比。对比分析结果表明该方法能有效的克服传统遗传算法(TGA)在圆度误差评定上存在的搜索稳定性差、易陷入局部收敛和全局搜索能力不足的问题，是一种更有效的圆度误差评定方法。

遗传算法;自适应;多种群遗传算法;圆度评定;最小区域圆法

0　引言

圆度误差是指回转体在任意横截面内被测实际圆对其理想圆的变动量。圆度误差是衡量回转体零件形状精度的一个重要指标，直接影响到机器零部件的旋转精度和装配精度。因此，准确的评定圆度误差是保证回转体零件加工精度和装配精度的重要依据[1]。

如何快速精确有效的评定圆度误差的大小一直受到国内外研究者们的广泛关注，圆度误差的评定方法有最小二乘法、最小区域圆法、最小外接圆法和最大内接圆法等方法。根据国标(GB1183—80)的规定，圆度误差须按最小区域圆法进行评定[2]。

与其他优化算法不同的是遗传算法属于全局搜索算法，具有较高的并行计算能力，对初始值的要求是解区间而非单个的点，全局搜索能力和鲁棒性好[3]。但传统遗传算法(TGA)在评定圆度误差时，存在以下不足：固定不变的交叉概率Pc和变异概率Pm并不符合算法各阶段的要求，会直接影响算法的全局搜索能力；TGA在算法快要找到最优解的时候，容易在最优解附近来回变动，局部搜索能力差，算法迟迟不能收敛，严重降低了算法的收敛速度；TGA停止的依据是到达规定的最大遗传代数，如果规定的最大遗传代数过小，进化不充分，也会造成未成熟收敛[1]；种群中个体更新只靠变异操作来维持，存在较大的随机性[4-5]。

本文根据圆度误差评定实际需要，改进遗传算法，提出自适应多种群遗传算法(AMPGA)对圆度误差进行评定，建立了多种群协同进化的遗传方式，并引入了交叉概率Pc和变异概率Pm随个体适应度值变化而不断调整的遗传机制，通过编写自适应多种群遗传算法(AMPGA)程序对圆度误差进行评定，并分别与三坐标实测圆度误差值和TGA评定的结果作对比，结果表明AMPGA能有效克服TGA在圆度误差评定上的搜索稳定性差、易陷入局部收敛和全局搜索能力不足的问题，同时在遗传代数、收敛速度方面，AMPGA要明显优于TGA，能快速准确的评定出圆度误差值，是一种有效的圆度误差评定优化算法。

1　自适应多种群遗传算法原理

多种群协同进化是加快遗传算法收敛速度的一个重要手段，用参数MP表示子种群数量,本文取MP=10。每个子种群独立执行遗传算法，所有子种群协同进化，选定遗传算法的参数GGAP=0.9[6]。

1.1个体适应度大小计算

本文采用采用实数编码遗传算法，适应度值函数采用线性排序函数：

(1)

式(1)中F为个体的适应度值，sp为选择压差1≤sp≤2，选择压差一般取1.5，P为个体在种群中的位置，N是子种群中的个体数量，本文取N=40。个体按ranking函数进行排序。

1.2选择操作

AMPGA的每个子种群在规定的遗传代数内分别独立的执行选择、交叉和变异操作。采用随机遍历抽样的方式，个体被选中概率用式(2)计算：

(2)

1.3自适应交叉和变异概率

为了改善TGA在圆度误差评定上的易陷入局部收敛和全局搜索能力不足的问题。本文提出了交叉概率Pc和变异概率Pm随个体适应度值自适应变化的遗传机制。

相比TGA中交叉概率Pc和变异概率Pm为固定值，AMPGA的交叉概率Pc和变异概率Pm是随着适应度值的变化自适应调整，在遗传算法前期如果交叉概率Pc过小，那么群体极容易陷入局部最优解，同样算法初期需要加强遗传算法的变异概率Pm，从而保证种群的多样性；到算法的后期，个体比较接近最优解，如果交叉概率Pc很大的话，则容易造成算法在最优解附近变化不收敛的情况。另外在种群中，适应度较大的个体应当施加较小的交叉概率Pc和变异概率Pm，使种群中的优良个体得以延续。而适应度小的个体则应当施加较大的交叉概率Pc和变异概率Pm。AMPGA交叉概率Pc与变异概率Pm调整公式为：

(3)

(4)

式(3)、式(4)中Fmax{i}表示第i个子种群中最大适应度个体的适应度值，Fave{i}表示第i个子种群平均适应度值，F{i}表示第i个子种群中个体的适应度值，t1代表适应度值大于或等于平均适应度值个体的序号，t2表示适应度值小于平均适应度值个体的序号；取Pc2=0.85，Pm2=0.05[7-8]。

1.4迁移操作和优良种群选择操作

为了改善TGA只靠变异操作来维持种群更新的随机性大弊端，本文引入了种群间迁移和优良种群选择的概念，种群间个体迁移是指在适应度值排序的基础上，从源种群中选择适应最大的个体迁移到目标种群中并替换掉目标种群中适应度最小的个体；优良种群选择操作是指在达到规定的遗传代数后，从所有子种群中选择最优的个体组成优良种群。AMPGA在达到规定的遗传代数，即最大保持代数gen0时，子种群间发生迁移，调用迁移算子，选择源种群中的适应度最大个体，替代目标种群中的适应度最小个体。AMPGA示意图如图1所示。

图1　AMPGA种群间迁移与优良种群示意图

1.5自适应多种群遗传算法停止的依据

AMPGA停止的依据是：某一代的优良种群中的最优解个体达到要求，即算法搜索到了全局最优解，当算法计算最小值时，某一代优良种群中的最优解不小于上一代优良种群中的最优解，gen0=gen0+1算法停止；否则最大进化代数gen0=0，再重复上述操作。同理，在计算最大值的操作过程中，当某一代优良种群中的最优解不大于上一代优良种群中的最优解，gen0=gen0+1算法停止；否则最大进化代数gen0=0，再重复上述操作。AMPGA流程如图2所示。

图2　AMPGA流程图

2　实验验证

建立AMPGA最小区域圆法圆度评定的目标函数。利用MATLAB平台，编写AMPGA和TGA程序，评定圆度误差。并与三坐标测量机的实测值对比。

本文的数据来源为海克斯康global07-10-07型三坐标测量机的实测值，对一圆柱体零件的一个横截面进行采样取点，一共在圆截面上采样30个点，覆盖整个圆周，测量零件圆度误差为0.0185mm，最小区域圆圆心点坐标为(-0.0018,0.0014)，单位为mm，海克斯康global07-10-07型三坐标测量机精度为次微米级，精度等级高，符合圆度评定要求。采样轮廓的被测点坐标P{(xj,yj)|j=1,2,……m}，采样点分布于整个圆周上，测点的最小值和最大值分别表示为xmin=min{xj}，ymin=min{yj}；xmax=max{xj}，ymax=max{yj}。被测点构成的圆的圆心(xc,yc)范围为xmin≤xc≤xmax，ymin≤yc≤ymax。取0≤a≤1,0≤b≤1，轮廓的圆心点坐标xc与yc可以表示为式(5)、式(6):

xc=xmin+a×(xmax-xmin)

(5)

yc=ymin+b×(ymax-ymin)

(6)

最小区域圆建立圆度误差评定方程，以此作为遗传算法的优化目标函数。目标函数优化参数分别为被测圆的最小区域圆的圆心的横坐标xc与纵坐标yc。同样考虑到遗传算法搜索时圆心点的横坐标和纵坐标取值是在坐标原点附近来回变化的，因此在本文中AMPGA和TGA取-1≤xc≤1,-1≤yc≤1。最小区域圆法圆度误差计算公式为：

e=min(rmax-rmin)

(7)

式(7)中rmax是最小区域法的两个同心圆外圆的半径，rmin是最小区域圆的两个同心圆内圆的半径[9-10]。测点到最小区域法圆心的距离用式(8)表示。

(8)

图3　圆度误差最小区域圆法示意图

算法的实质是搜索最小区域法同心圆的圆心点坐标，这样的同心圆有无穷多个，但只有一对同心圆的半径差是最小的，这个最小差值就是圆度误差值。

3　数据的对比分析

3.1三坐标测量机测取点

本文利用海克斯康global07-10-07 三坐标测量机在圆柱体零件外表面上测取30个点，这些点覆盖整个圆周，符合圆度评定的要求。在pc-dmis软件选择评定方式为最小区域圆法，评定的圆度误差值为0.0185mm，最小区域圆圆心点坐标为(-0.0018,0.0014)，单位mm，海克斯康global07-10-07 型三坐标测量机精度是次微米级。实际测量的测点横坐标xi和纵坐标yi记录如表1所示。

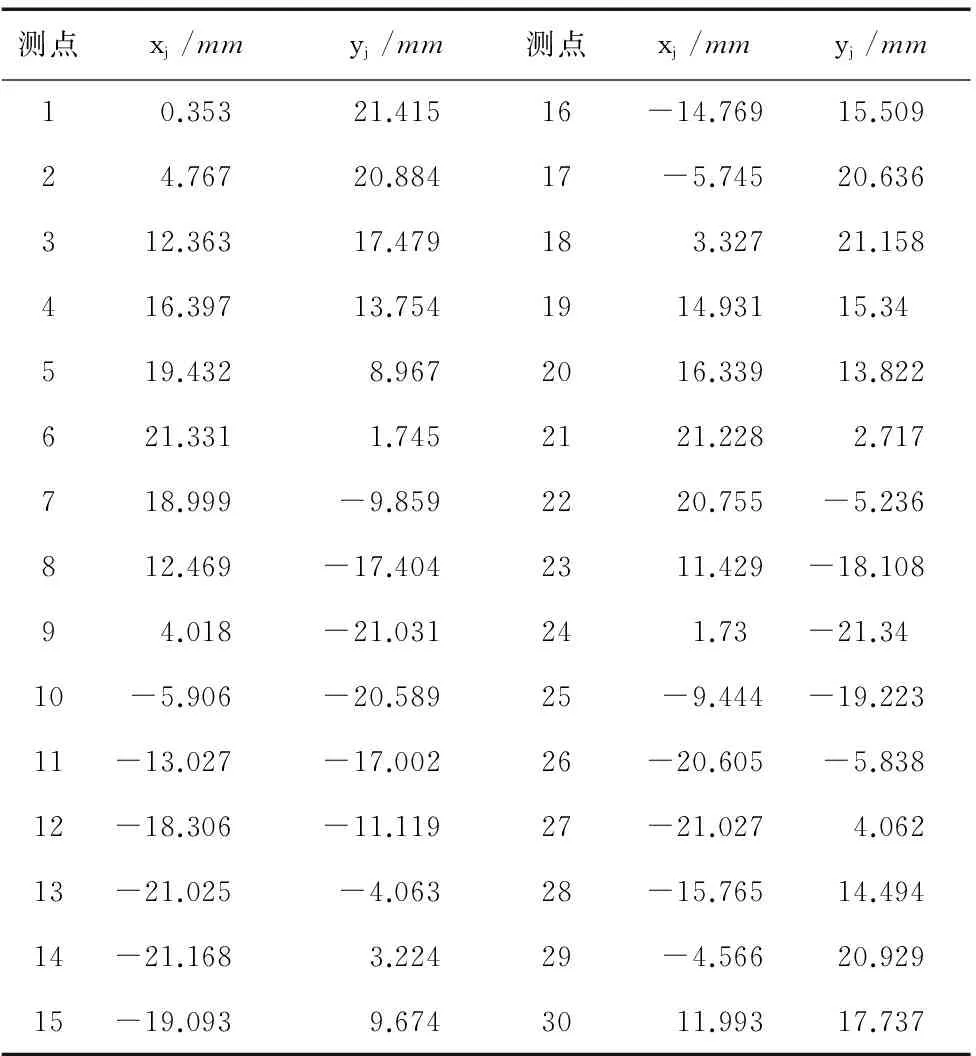
表1　测点的坐标

3.2利用程序评定圆度误差

将测点数据分别导入到AMPGA与TGA程序中，利用算法程序分别评定圆度误差值，各自计算10次，记录下圆心点坐标值xc、yc和圆度误差值e，取小数点后三位有效数字。传统遗传算法中取最大遗传代数MAXGEN=1000，自适应多种群遗传算法中取最大保持代数MAXGEN=500[9-10]，计算结果如表2所示。

表2　TGA与AMPGA评定结果对比

从表2中可以看出AMPGA的稳定性明显优于TGA，AMPGA的相对误差δ稳定0.07%左右，而TGA的相对误差δ均值为2.4%，表现的很不稳定。同样在最小区域圆圆心点坐标的评定上，AMPGA也表现出了良好的稳定性，圆心点的横坐标和纵坐标值都相对稳定，且明显优于TGA。

3.3最优解随遗传代数变化过程

利用算法程序记录下优良种群中最优解的变化过程，算法计算到某一代是最优解不再发生变化，此时算法收敛，即算法搜索到了全局最优解。图4是AMPGA最优解随遗传代数的变化曲线图，图5是TGA最优解随遗传代数的变化曲线图。

图4　AMPGA进化过程图

图5　TGA进化过程图

由图4可以看出AMPGA在计算到100左右时，最优解的值基本趋于稳定，即算法到达成熟收敛，找到了全局最优解，此时的最优解即为评定的圆度误差值；由图5可以看出TGA在算法计算到400代左右时，仍然没有收敛，算法并没有趋于稳定。由此看出AMPGA在遗传代数上要明显小于TGA收敛速度更快。

4　结论

通过改进传统遗传算法，利用MATLAB平台，建立了AMPGA与TGA最小区域圆法圆度评定的目标函数，通过编写算法程序，分别对AMPGA和TGA做了最小区域圆法圆度评定。通过与三坐标测量机的实测值对比分析，得出以下结论：

(1)AMPGA对遗传算法中的两个重要参数交叉概率Pc和变异概率Pm运用自适应取值，根据个体在不同的进化阶段适应度的线性排序自适应取值，保证了种群的多样性，能有效克服传统遗传算法的未成熟收敛。

(2)AMPGA属于多种群并行遗传算法，收敛速度明显高于TGA。引入种群间迁移算子和优良种群选择算子改变了TGA仅靠变异更新个体随机性大的弊端。AMPGA在100代左右就能搜索到全局最优解，而TGA在400代左右仍表现的很不稳定性，并未达到全局收敛。多次计算的结果表明AMPGA在收敛速度和稳定性方面优于TGA。

[1] 缪立栋,郭慧,张帆.基于多种群实数编码遗传算法的圆度误差评定[J].工程图学学报,2010(2):43-48.

[2] 刘飞，梁霖，徐光华，等.一种圆度误差最小区域评定方法[J].组合机床与自动化加工技术,2011(7):48-51.

[3] 陈飒，李郝林.基于改进遗传算法的圆度误差评定[J].机械设计与制造,2006(1):20-21.

[4] 谢耿勋.基于遗传算法的性状误差算法的研究[D].沈阳:东北大学,2012.

[5] 史峰.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.

[6] 雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2004.

[7] 廖平.用遗传算法精确计算圆度误差[J].南京航空航天大学学报,1999,31(4):393-397.

[8]PottsJC,GiddensTD,YadavSB.Thedevelopmentandevaluationofanimprovedgeneticalgorithmsbasedonmigrationandartificialselection[J].IEEETransonSMC,1994,24(1):73-86.

[9] 周剑平.基于MATLAB的圆度评定方法[J].计量与测试技术,2005,32(2):5-7.

[10] 张国强.自适应遗传算法的改进与应用[J].舰船电子工程,2010,30(1):83-85.

(编辑李秀敏)

RoundnessErrorEvaluationBasedonAdaptiveMultiplePopulationGeneticAlgorithm

LIUSi-yao1,HUANGMei-fa1,2,FENGJian-guo2,CHENGBin-bin1,WUFen1,WUChang-lin1

(1.SchoolofMechanicalandElectricalEngineering,GuilinUniversityofElectronicTechnology,GuilinGuangxi541004,China; 2.GuilinMachineToolCo.,Ltd,GuilinGuangxi541000,China)

Thetraditionalgeneticalgorithm(TGA)roundnesserrorevaluationarepoorstability,prematureconvergenceandinsufficientofglobalsearchability.Thispaperimprovethetraditionalgeneticalgorithm(TGA),putforwardtheadaptivemultiplepopulationgeneticalgorithm(AMPGA)roundnesserrorevaluationmethod.Basedonthecharacteristicsofroundnesserrorevaluation,weestablishmultiplepopulationsco-evolutionarygeneticalgorithm,andintroducetheadjustmentofcrossoverprobabilityandmutationprobabilitywiththeindividualfitnessvaluechanging.Wewriteadaptivemultiplepopulationgeneticalgorithm(AMPGA)programandworkouttheroundnesserror.Andcomparethecorrespondingresultswiththemeasuredvaluesofthreecoordinatemeasuringmachine.ThroughthecontrastanalysisresultsprovethattheAMPGAcaneffectivelyovercomepoorsearchstability,prematureconvergenceandinsufficientofglobalsearchabilityontheroundnesserrorevaluation,TheAMPGAisamoreeffectivemethodofroundnesserrorevaluationcomparewithTGA.

geneticalgorithm(GA);adaptive;multiplepopulationgeneticalgorithm(AMPGA);roundnesserrorevaluation;minimumzonecircleroundnesserrorevaluation

1001-2265(2016)08-0096-04DOI:10.13462/j.cnki.mmtamt.2016.08.027

2015-09-06；

2015-10-09

国家自然科学基金资助项目(51365009)；广西制造系统与先进制造技术重点实验室主任课题资助项目(13-051-09-009Z)；桂林电子科技大学研究生教育创新计划资助项目(YJCXS201501)

刘思遥(1988—)，男，湖南永州人，桂林电子科技大学硕士研究生，研究方向为现代设计与制造技术，(E-mail)309141622@qq.com。

TH164;TG506

A