集成传感功能的介电弹性体驱动器研究*

朱银龙，葛路伟，周宏平，王化明

(1.南京林业大学 机械电子工程学院，南京 210037；2.南京航空航天大学 机电学院，南京 210016)



集成传感功能的介电弹性体驱动器研究*

朱银龙1，葛路伟1，周宏平1，王化明2

(1.南京林业大学 机械电子工程学院，南京 210037；2.南京航空航天大学 机电学院，南京 210016)

以介电弹性体材料为研究对象，设计一种集成传感功能的往复式直线驱动器。分析直线驱动器的工作原理，利用一个驱动单元的力行程曲线叠加构成直线式驱动器的工作特性曲线。建立介电弹性体驱动器的数学模型，利用数值解法计算出电压激励下介电弹性体驱动器的工作行程与输出力之间的关系，给出驱动器长度与工作行程的关系。同时给出驱动器工作过程中，介电弹性体薄膜内部的应力和应变分布情况，并给出驱动器不同工作位置的传感器电容值。试验结果与分析结果较好吻合，研究结果可以为介电弹性体驱动器的设计提供有力的支持。

介电弹性体；驱动器；传感器；建模

0　引言

近年来，一种新型智能材料—介电弹性体以其具有的大变形(380%)、驱动效率高、重量轻等优点，在应变量、驱动力能量密度等方面最为接近自然肌肉[1-2]，引起世界各国研究人员的广泛关注。自上世纪九十年代末，美国斯坦福研究院(SRI)一直致力于相关方面的应用研究，并成立了专门的公司(AMI)从事相关产品的设计开发[3-4]。在理论研究方面，哈佛大学的Suo Zhigang教授[5-6]提出了介电高弹聚合物理论，为介电弹性体的大变形、力电耦合失效、能量转换效率研究奠定了理论基础。在新型器件的制备方面，伦敦大学的Carpi[7-8]研制了一种用于力反馈研究的静态液压耦合的介电弹性体驱动器，驱动器由主动单元和被动单元两部分构成，通过液体实现两者之间的力传递。Lochmatter等研究了DEAP驱动的单自由度摆动关节[9-10]，采用两个平面形驱动器推拉关节结构实现摆动，将多个关节串联得到大范围的摆动，但关节结构尺寸较大。近年来，国内的哈尔滨工业大学[11]、南京航空航天大学[12-14]也开展了理论与应用研究。现有的研究表明，介电弹性体在新型驱动器、传感器、能量收集和软体机器人等领域存在潜在的应用前景。

在驱动器方面，介电弹性体驱动器主要结构可分为[15]：圆柱型、锥型、菱形、推拉式等。其中，圆柱形驱动器制作较为复杂，但结构紧凑；菱形驱动器和推拉式驱动器输出力可观，但体积较大，锥形驱动其性能与体积相对折中。

分析了介电弹性体驱动器的工作原理、提出将两个锥型驱动器反向放置，利用一个驱动器的弹性薄膜作为另一驱动器的预载，设计了一种具有传感功能的直线型驱动器，并建立驱动器的分析模型。通过模型求解分析了驱动器在不同电压激励下的静态输出特性。该直线型驱动器有望应用于医学上的精确给药、MEMS微型换能器等领域。

1　介电弹性体驱动器工作原理

介电弹性体是一种超弹性绝缘材料，其工作过程本质上是一可变电容器。在介电弹性体表面两侧覆盖柔性电极后并施加高压激励，产生的静电压力使得介电弹性体薄膜面积方向扩展、厚度方向收缩。此过程中，电能转变为机械能。由于介电弹性体薄膜是一种软材料，需要其他结构将其张紧。如图1a所示[16]，将介电弹性体薄膜预拉伸后利用内外框架将其固定构成驱动单元，然后两个驱动单元反向对置内框连接固定构成图1b所示的直线型驱动器。直线型介电弹性体驱动器可以视为一变刚度弹簧，通电前后的刚度不同，通电前两个拉伸弹簧处于平衡状态，将左侧通电后其刚度变小，在右侧弹簧的作用下向右运动；反之，则向左运动。此过程中，可测量未通电一侧的电容值变化来确定驱动器的输出力和工作位置，在功能上实现驱动传感于一体。

图1　直线型驱动器结构

从驱动器的工作原理可见，如果能确定不同激励电压时驱动器的平衡位置，则可确定驱动器的静态工作特性。为此，讨论单一驱动单元在激励电压作用下的力—位移曲线。如图2所示，曲线fr(z)为通电时的推程力—位移曲线，fs(z)表示断电时的回程力—位移曲线。曲线fs(z)与fr(z)间围成的面积(记为Wm-c)等于驱动单元工作时可输出的总机械能。将两个驱动单元的力—位移曲线按照图2所示的工作原理进行叠加，可以得到如图3所示的直线型驱动器力—位移曲线。

图2　通电前后驱动器力—位移曲线

图3　直线型驱动器工作过程示意图

图3中，A点为直线型驱动器内框初始位置，左侧驱动单元通电时，左侧薄膜刚度降低，在右侧驱动单元的拉伸作用下，驱动器内框向右侧运动，曲线fsr(z)表示驱动器向右运动时的力-位移曲线，从A点运动到C点后，驱动器达到平衡位置。此时，左侧驱动单元断电，驱动器左侧薄膜刚度升高，拉动右侧薄膜向左侧沿力-位移曲线DA运动到初始位置A点，至此驱动器完成一个工作循环ABCDA。同理，将右侧驱动单元通电，驱动器向左侧运动，断电后回到初始位置A点，完成另一循环ADFGA。图中两个平衡位置FC之间距离表示直线型驱动器往复运动的总行程，OH表示直线驱动器两个外框之间的距离，即驱动器长度尺寸。若能得到图4所示的曲线准确数值及平衡点位置，则可确定驱动器的基本输出特性。

图4　介电弹性体驱动单元变形后截面形状

2　介电弹性体驱动单元的数学模型

介电弹性体薄膜预拉伸之前为一圆环面，取薄膜上一点P进行分析，在初始坐标系(R,Θ,Z)中表示为P(R,Θ,Z)，薄膜拉伸后内、外径处用框架固定，形成一锥形轴对称回转体，其截面形状用图4表示。变形后P点在当前坐标系(r,θ,z)中记为p(r,θ,z)。P点附近微元长度dR在当前坐标系下为弧长ds，那么根据变形前后的几何关系，可将经向、纬向和法向延伸率表示如下：

(1)

(2)

式中λ1，λ2，λ3是经向、纬向和法向延伸率，r1,r2表示经线和纬线方向的曲率半径。θ是曲线s上p点处的法线方向和z轴夹角。

利用薄膜无矩理论对介电弹性体薄膜进行分析，驱动单元的平衡方程为:

(3)

式中σ1、σ2为经线和纬线方向的薄膜真实应力，h0为预拉伸前的薄膜初始厚度，F为z轴方向驱动器内框所受的预紧力。

由于薄膜厚度足够小，薄膜两边的静电压力是大小相等、方向相反的，因为厚度方向的尺寸与平面方向的尺寸相比非常小，可以假设薄膜法向应力为零，那么平面方向的两个主应力可以表示为：

(4)

式中W表示应变能方程，ε0,εr为真空介电常数和相对介电常数。采用Yeoh形应变能方程，将式(1)、(2)、(4)代入式(3)整理后表示如下:

(5)

驱动器的电容值可以表示为:

(6)

对于两个驱动单元对称放置，式(5)中U取零值表示通电的一侧，U取非零值表示未通电一侧。两侧单元互相给对方施加预紧力F，如能确定在某个位置z对应两个驱动单元的不同构型，满足式(5)这一微分代数方程组，则完成式(5)的求解。

3　数值计算结果与分析

编写程序求解微分代数方程组式(5)，可以得到驱动单元的力—位移曲线、介电弹性体薄膜内部的应力、延伸率分布。选取换能单元内外直径尺寸分别为30 mm、80 mm，薄膜初始厚度为2 mm，薄膜预拉伸率为375%进行理论分析。图5为驱动单元在8.5kV激励电压时的力—位移曲线，随着激励电压的增加，驱动单元的力曲线往下移动，与断电回程曲线之间的距离逐渐增加。导致这一现象的原因是随着电压的增加，产生的静电力也越大，从而不断降低薄膜内张力的缘故。图6表示驱动单元位移与电容值之间的关系，从图6可以看出，电容曲线与位移表现出非线性关系，当位移大于15mm后，近似表现为线性关系。

图5　驱动单元理论力—位移曲线　图6　驱动器理论电容值

选取驱动器长度尺寸为20mm，即两个驱动单元分别预拉伸10mm。通电8.5kV时，经过计算可以得到图7所示的驱动器力-行程曲线。通电瞬间，驱动器输出力约为1.32N，达到平衡位置后断电瞬间驱动器输出力约为2.15N，驱动器左右两侧皆可输出6.1mm位移，往复行程为12.2mm。在右侧平衡位置时，左右驱动单元的介电弹性体薄膜外形截面如图8所示，可见左侧驱动单元变形较大，截面形状近似梯形，而右侧单元回缩后形状近似锥形。

图7驱动器理论力—位移曲线　图8通电后驱动器截面示意图

左侧驱动单元通电时，驱动器内框向右运动，达到最大行程时，左侧驱动单元被拉伸，右侧驱动单元被压缩，此刻两个驱动单元内部的经向和纬向延伸率分布如图9和图10所示。可见，由于通电侧变形较大，所以对应的延伸率也比较大。而为通电侧变形较小，两个方向的延伸率比预拉伸率375%略大。图11和图12所示为驱动器薄膜两个方向的真实应力分布。

图9驱动器薄膜经向延伸率　图10驱动器薄膜纬向延伸率

图11驱动器薄膜经向真实应力图12驱动器薄膜纬向真实应力

图13为驱动器的工作行程与驱动器长度的关系，可见驱动器的初始长度(两个驱动单元外框间距)对驱动器的工作行程具有较大影响，两者之间并非单调关系，对于此次分析所取内外径30 mm、80 mm的驱动单元而言，初始长度从20变化至40mm时，驱动器单侧工作行程在6～6.5mm范围内变化，那么两侧依次通电时驱动器工作行程可达12～13mm。

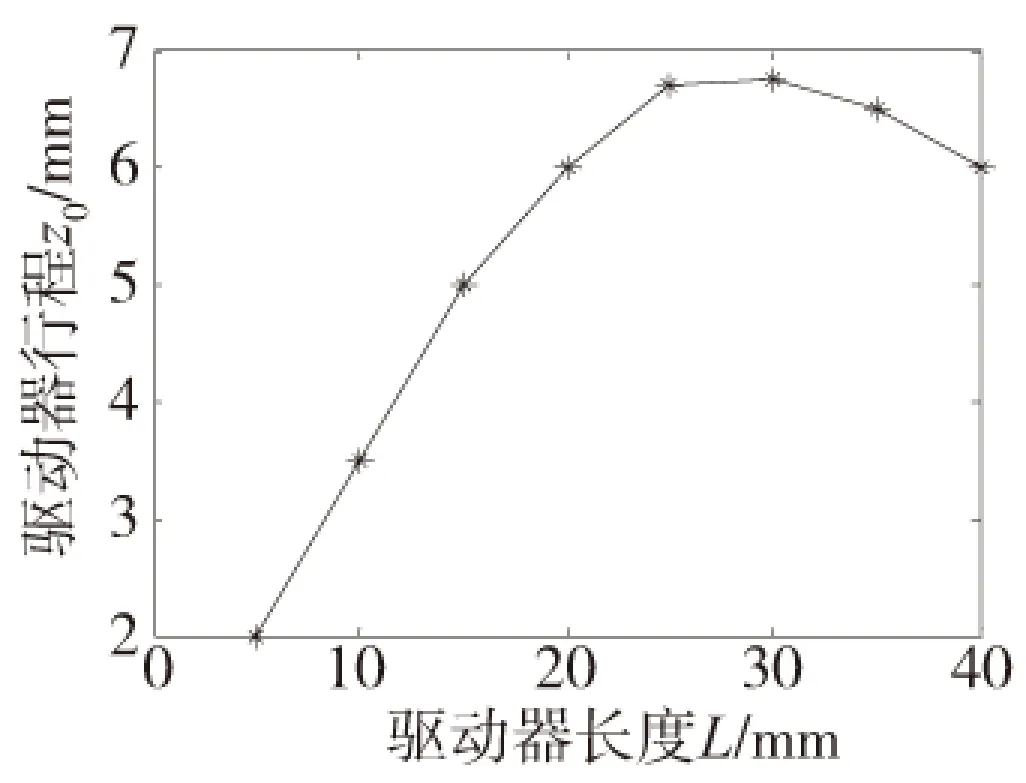
图13　驱动器长度与行程关系

4　试验结果

将两层VHB4910叠加后等轴拉伸375%，用内外框固定。薄膜两侧涂上柔性电极放置半小时后，组装成反向放置的驱动器。利用图14所示的激光传感器拉伸平台配合激光传感器和力传感器依次测试驱动器通断电时的输出位移和相应的驱动器输出力曲线，同时利用LCR测试驱动器未通电一侧单元的电容值。

图14　试验平台照片

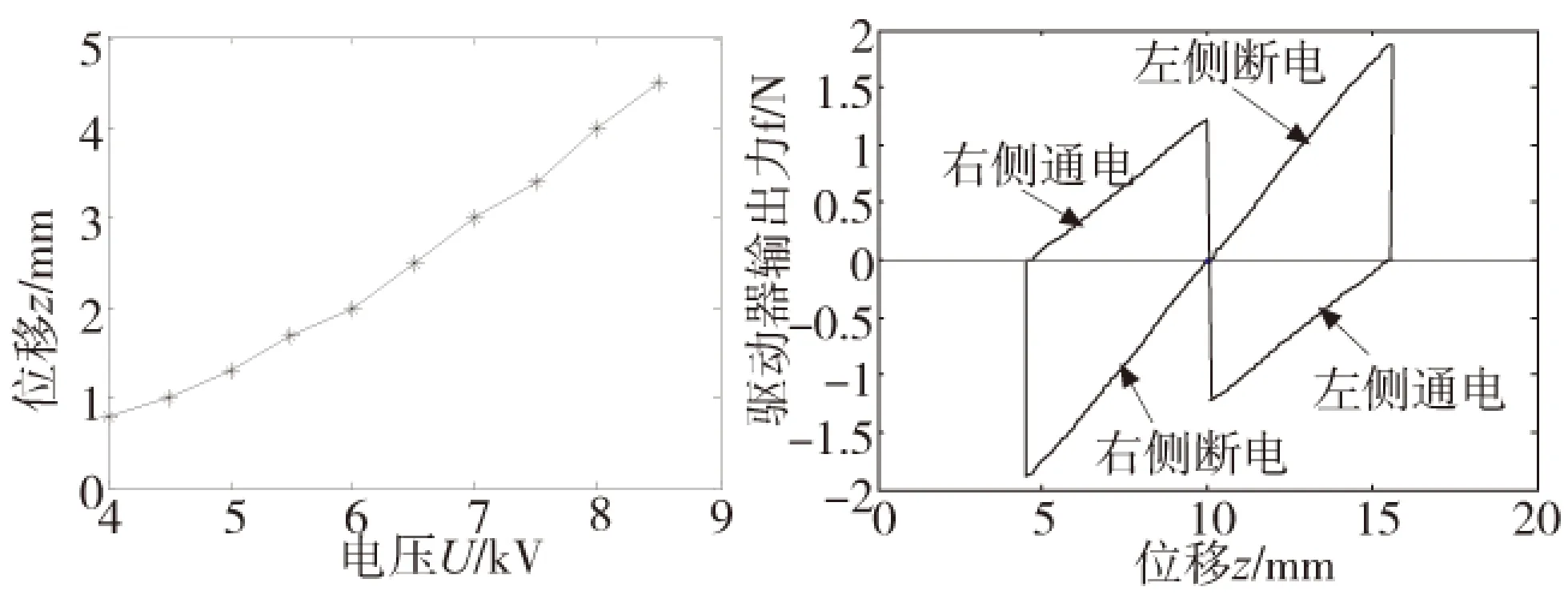
图15　直线驱动器输出位移曲线　图16　直线驱动器理论力输出曲线

试验结果如图15所示，为施加不同激励电压时驱动器的输出位移。施加4kV～8.5kV电压时，驱动器输出位移依次增加。图16为相应的驱动器输出力曲线，可见通电8.5kV时，驱动器推程最大输出力为1.23N，断电时回程最大输出力为1.88N，整个曲线和图7分析的理论曲线数据基本一致。图17所示为驱动器的电容值，LCR测得的电容与图6所示的理论电容值比较吻合。图15直线驱动器输出位移曲线图16直线驱动器理论力输出曲线

图17　驱动器试验电容值

5　结论

(1)利用锥形驱动单元构建了一种集驱动传感功能于一体的直线型驱动器。

(2)建立驱动器的数学分析模型，给出驱动器的输出力位移曲线、两侧薄膜的应力应变分布情况及启动单元的电容值。分析结果表明，驱动器初始长度、激励电压影响驱动器的输出位移。

(3)试验结果与理论分析基本吻合，从而验证了理论建模的正确性。本文研究结果可以为介电弹性体驱动器的设计提供理论指导。

[1] Deepak T, Christopher D R, William M K, et al. Soft robotics: Biological inspiration, state of the art, and future research[J]. Applied Bionics and Biomechanics, 2008, 5(3): 99-117.

[2] Brochu P, Pei Q B. Advances in Dielectric Elastomers for Actuators and Artificial Muscles [J]. Macromolecular Rapid Communications, 2010, 31:10-36.

[3] Prahlad H, Kornbluh R, Pelrine R，et al. Polymer Power Dielectric Elastomers and Their Applications in Distributed Actuation and Power Generation [C]. Proceedings of ISSS 2005 International Conference on Smart Materials Structures and Systems, Bangalore, India, 2005, SA-13.

[4] Chiba S, Waki M, Kornbluh R, et al. Innovative power generators for energy harvesting using electroactive polymer artificial muscles [C]. Electroactive Polymer Actuators and Devices (EAPAD), edited by Yoseph Bar-Cohen, Proceedings of SPIE, San Diego, California, USA: 2008, 6927: 15-1-15-9.

[5] Suo Z G, Zhao X H, Greene W H. A nonlinear field theory of deformable dielectrics [J]. Journal of the Mechanics and Physics of Solids, 2008, 56: 467-486.

[6] Suo Z G, Zhao X H, Wei H, et al. A theory of large deformation in soft active materials[C], Electroactive Polymer Actuators and Devices (EAPAD) 2008, edited by Yoseph Bar-Cohen ,Proc. of SPIE ,2008,6927: 277-786.

[7] Carpi F, Frediani G, Rossi D D .Electroactive elastomeric haptic displays of organ motility and tissue compliance for medical training and surgical force feedback[J]. IEEE Transactions on Biomedical Engineering, 2009, 56(9):2327-2330.

[8] Carpi F, Frediani G, Rossi D D. Opportunities of hydrostatically coupled dielectric elastomer actuators for haptic interfaces. Electroactive Polymer Actuators and Devices (EAPAD) 2011, edited by Yoseph Bar-Cohen, Federico Carpi, Proc. of SPIE 2011,7976:797618-1-797618-9.

[9] Kovacs G, Lochmatter P, Wissler M. An arm wrestling robot driven by dielectric elastomer actuators [J]. Smart Materials and Structures, 2007, 16: S306-S317.

[10] Lochmatter P, Kovacs G. Design and characterization of an actively deformable shell structure composed of interlinked active hinge segments driven by soft dielectric EAPs [J]. Sensors and Actuators A, 2008, 141: 588-597.

[11] Liu Y J, Liu L W, Sun S H, et al. Electromechanical stability of a Mooney-Rivlin-type dielectric elastomer with nonlinear variable permittivity [J]. Polymer international. 2010, 59(3):371-377.

[12] 罗华安，王化明，游有鹏.介电弹性体圆柱形驱动器静态特性分析[J].农业机械学报，2012，43(9)：202-208.

[13] 吴孟, 王化明, 朱银龙,等. 圆柱形介电弹性体驱动器的试验与分析[J]. 机器人, 2010, 32(6): 754-758.

[14] Wang Huaming, Zhu Yinlong, Zhao Dongbiao, et al. Performance Investigation of Cone Dielectric Elastomer Actuator Using Taguchi Method[J], Chinese Journal of Mechanical Engineering, 2011, 24(4): 685-692.

[15] Brouchu P, Pei Q B. Advances in Dielectric Eleastomers for Actuators and Artificial Muscles [J]. Macromolecular Rapid Communications, 2010, 31:10-36.

[16] Marcus Rosenthal, Chris Weaber, Ilya Polyakov,et al. Designing Components Using smartMOVETMElectroactive polymer technology[J]. Electroactive Polymer Actuators and Devices (EAPAD) 2008, edited by Yoseph Bar-Cohen Proc.2008,6927:692704-1-692704-12.

(编辑李秀敏)

Research on Dielectric Elastomer Actuator Integrated with Sensor

ZHU Yin-long1，GE Lu-wei1，ZHOU Hong-ping1，WANG Hua-ming2

(1.College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China; 2. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

An actuator of straight reciprocating with sensor integrated based on dielectric elastomer actuator was proposed. Working principle of linear actuator was analyzed and force-stoke curve of actuator was determined by combing force-stroke curves of two actuation unit. Moreover, mathematical model of actuator was presented, with which force output and working strokes of dielectric elastomer actuator, relationship between length of actuator and strokes of actuator and were explored. In addition, true stress, stretch ratio of dielectric elastomer membrane and capacitance of sensor at different position were all given. Experimental results agree well with the theoretical one, which demonstrate that this job can guide the design of dielectric elastomer actuator.

dielectric elastomer；actuator；sensor；modeling

1001-2265(2016)08-0005-04

10.13462/j.cnki.mmtamt.2016.08.002

2015-07-12

国家自然科学基金资助项目(51305209)；江苏省自然科学基金资助项目(BK20130979, BK2011735)；中国博士后科学基金资助项目(2013M541678)

朱银龙(1981 —)，男，江苏东海人，南京林业大学讲师，博士后，研究方向为介电型电活性聚合物换能器的研究，(E-mail)zhuyinlong@nuaa.edu.cn。

TH132;TG506

A