顾及几何特征的规则激光点云分割方法
方 军,李朝奎,张新长,张 强,廖孟光,卜 璞
(1. 湖南科技大学地理空间信息技术国家地方联合工程实验室,湖南 湘潭 411201;2. 湖南科技大学地理空间信息湖南省工程实验室,湖南 湘潭 411201)
顾及几何特征的规则激光点云分割方法
方军1,2,李朝奎1,2,张新长1,2,张强1,2,廖孟光1,2,卜璞1,2
(1. 湖南科技大学地理空间信息技术国家地方联合工程实验室,湖南 湘潭 411201;2. 湖南科技大学地理空间信息湖南省工程实验室,湖南 湘潭 411201)
三维激光扫描仪能快速地获取三维场景的高精度点云数据,已成为快速三维建模的重要工具。点云分割是三维点云模型数据预处理中的首要环节,也是影响重建效率与模型质量的重要因素。以激光点云的分割为研究切入点,以八叉树空间划分方式对数据进行组织,并用八进制编码进行命名,结合K邻近搜索法获取目标点的局部邻近点,采用加权平均目标点相邻的三角面片法向量来估算单点法向量。基于投影欧氏距离拟合曲面求取曲率。量化了规则点云集的分割约束条件,采用法向量信息来进行平面点的提取,根据曲率在两个主方向上的差异性来识别和分割柱面和球面信息。试验结果表明:①基于法矢量的平面点分割效果理想;②基于曲率差异性的规则曲面点分割效果较差;③基于几何特性的规则激光点分割方法合理可行。
激光点云;空间划分;邻近点;点云分割;法矢量;曲率
三维激光扫描技术以其精度高、采集数据速度快、数据格式简单,可操作性强等特点在三维数字城市建模过程中占有一席之地[1-2]。近年来,激光技术和通信技术的研究取得了重要突破,使得三维激光扫描仪得到广泛应用。三维激光扫描仪是根据红外线的高速发射与返回接收来获得建筑物的特征信息,尤其是其表面的空间信息。观测对象的表面空间信息是以点的方式表现出来的,点与点之间是分散布局的,彼此之间没有明显的空间拓扑关系的离散点[3]。因此在其使用过程中,用户普遍反映出一些问题,如获取的数据规模太大,后续的数据处理工作量大、繁杂琐碎等,使得模型建立效率过低。当前三维点云建模中出现的问题,可以归结为3种主要矛盾:①数据量大、手工建模劳动强度大的难题与现状模型重建的效率和精度要求高之间的矛盾;②分块建模后几何模型缺乏拓扑关系、几何特征参数不能获取与当前要求空间数据快速检索与处理之间的矛盾;③不能对象化及规则化描述精细三维模型,纹理信息不全且计算复杂与当前建立高逼真性、高精细化模型之间的矛盾。
针对点云数据离散、无直接拓扑关系的特点,目前的三维激光后数据处理软件主要包含以下的处理功能[4]:初始数据的滤波除噪,多测站数据的融合与配准,三维数据的特征分割与提取,三维点云面片的重建与显示。由于复杂、不规则物体的扫描数据往往更加难以用统一的数学公式和计算机语言对其进行描述和表达,造成现在的数据分割主要通过人工或半人工方式得以完成,工作量庞大、耗时且效率低下[5]。针对三维数据处理与三维重建中存在的问题,选择三维数据分割作为研究切入点,通过建立有效的点云分割方法,根据邻近点拟合成目标表面所体现出的目标点的几何特征,将大量的点云数据分割成不同类型的点的集合,采用聚类的方法完成点云聚类,再根据不同类型数据的特征,运用相应的数学模型对点集进行三维重建。该方法有助于解决海量点云数据的存储管理及点云数据的高效分割难题,进而为点云数据的三维重建奠定基础。
一、空间数据划分方法
1. 八叉树空间划分
空间八叉树(Octree)划分方法是平面四叉树方法在维度上的一个升级,目的是为了达到将复杂三维物体简化的目的。如图1所示,取一个立方体空间,将其在6个面的垂直中分面处进行空间8等分,得到了8个空间结构一致的子立方体,称为8个体元[6-7]。依此类推,直至子节点符合划分条件后不再对其进行划分。在递归式的八叉树空间划分过程中,要判断每个级别中的子立方体中所包含的三维空间点的数量,如果数量为零,则该子立方体的空间划分到此结束,如果其数量不为零,则继续执行空间划分,直至满足应用需求。
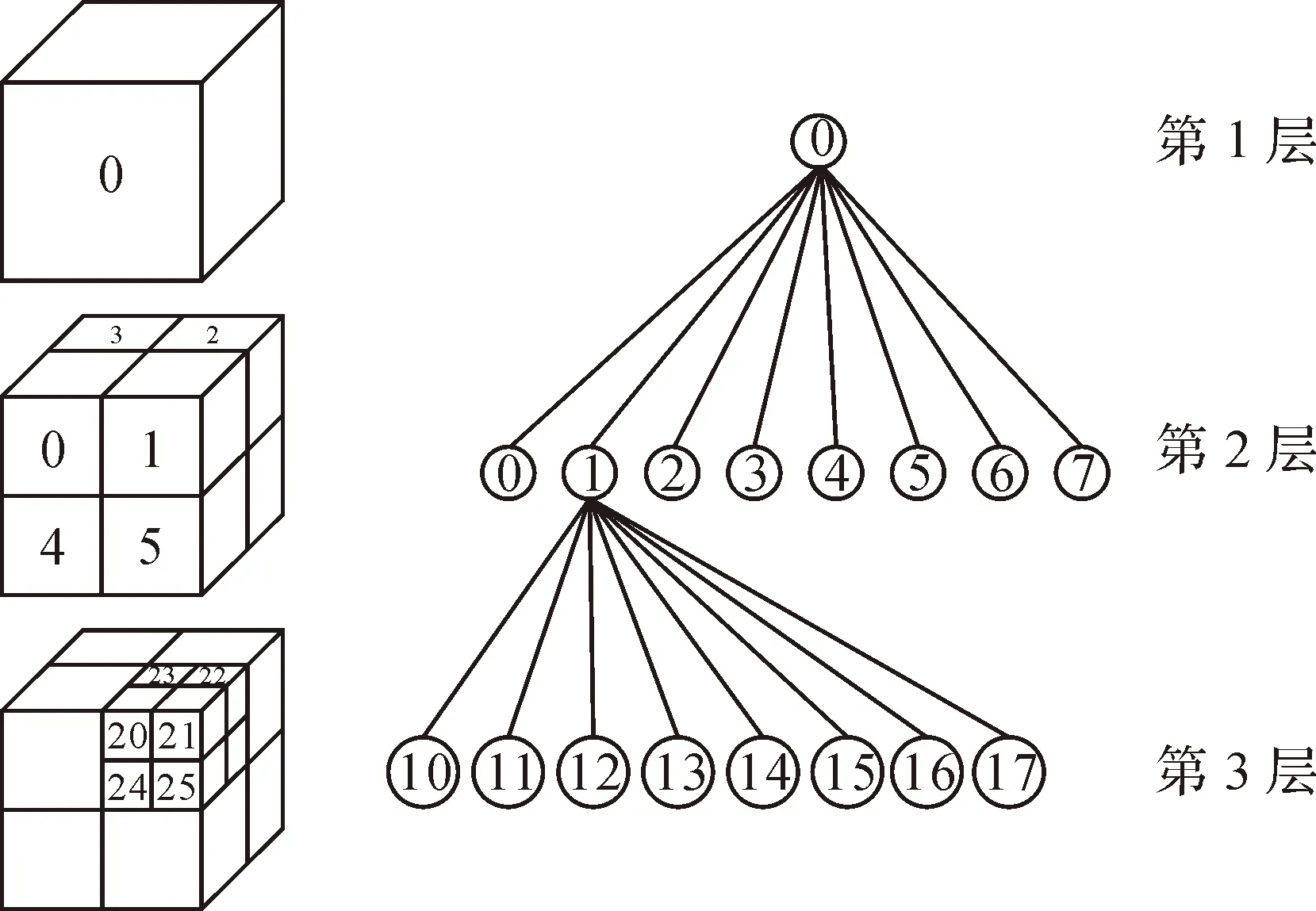
图1 八叉树空间结构
八叉树空间划分方法思路清晰,结构简单,在点云数据处理中有两个主要优势:
1) 八叉树空间划分的存储方式使得数据按空间分开存储,提高了数据在调用时的效率,降低了内存的使用率。
2) 八叉树空间划分完成后,叶节点的访问及修改成本低。
2. 八叉树分割流程
结合八叉树空间划分的思想和空间划分的终止条件(如图2所示),将八叉树的划分算法归结如下:
1) 遍历整个点云集,查出点的坐标值在3个正交轴向上均为最大和最小的点,记作(xmax,ymax,zmax)和(xmin,ymin,zmin)。根据该点云集的空间跨度,选择合适的微分量ρ,以上一步中的两点的坐标值为参照,对八叉树空间的边界进行微调,得出八叉树空间最终边界值(xm,ym,zm)和(xn,yn,zn),根据边界坐标构建点云的最小空间体。
2) 对八叉树的根节点立方体进行首次八叉树结构划分,并依据上文所提及的空间编码方法和编码顺序对得出的8个空间子立方体进行八进制编码。并将各子立方体空间所包含的点云数据存储到其八进制编码所对应的集合中,建立空间点与子立方体的对应关系。
3) 选取合适的子立方体包含点数阈值γ,对上一步中的8个子立方体进行判断,如果子立方体中点的数量大于阈值γ,则将该子立方体当作根节点返回至步骤2)进行第2级的划分,否则进行下一步。
4) 判断子立方体中点的数量,如果数量不为零,则确定子立方体编码与其内部点集的对应关系;如果数量为零,则该空间子立方体为冗余空间,空间不保存。
5) 反复迭代执行步骤3)和4),直至所有子立方体满足划分要求,那么点云的八叉树索引基本建立。
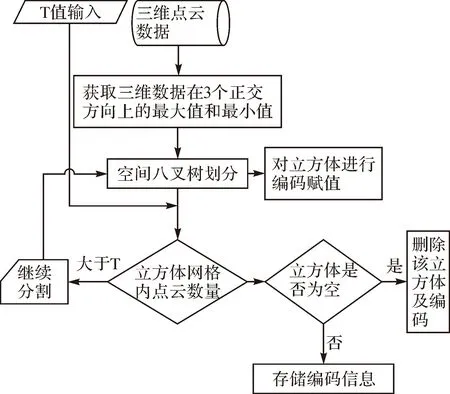
图2 八叉树网格划分流程
3. 八叉树分割终止条件
现阶段主要形成两类分割终止的依据[8]:一种是根据分割后子立方体的空间大小进行判断,即判断子节点立方体的体积或各边的长度,如果分割后子立方体的体积小于预先设定的阈值,或边长小于一定的阈值,则停止划分,否则继续进行迭代分割,直至该判断条件成立,八叉树空间划分得以完成;另一种方法是针对点云数据的空间划分而言,即基于子立方体中包含的点云数量的方法,以子节点中点的数量为判断依据,决定该子节点是否进行下一级别的划分。图3是划分终止条件示意图。
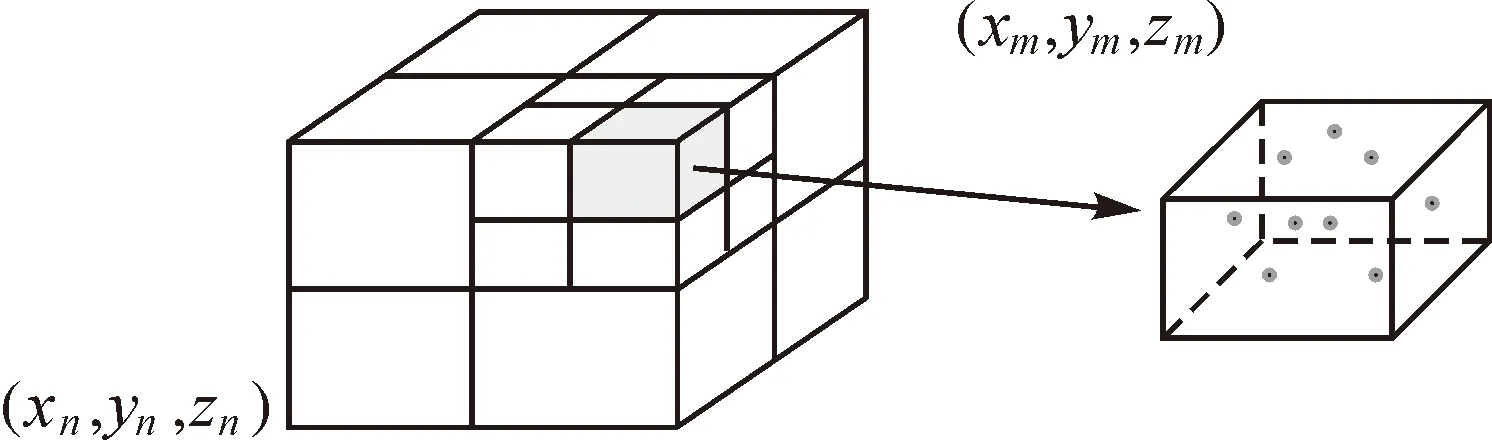
图3 空间划分终止条件
判断条件γ阈值的取值显得尤为重要,根据以往试验结果得知,如果γ阈值的取值太大,则分割没有到最优化,没有完美的体现八叉树划分的高效存储管理优势;如果γ阈值的取值过小,则必然使得空间八叉树产生的级别过深,同样影响索引速度,导致点云数据支离破碎,破坏其连贯性。γ阈值的取值受点云密度的影响,同时也跟八叉树划分的深度有一定的关系。
二、点云几何特征量解算
1. 加权平均法求取法矢量
离散点云的法矢量是点在空间分布的重要特征,因此估算点的法向量成为点云分割过程中的一个重要环节。一些学者采用各种拟合算法,将P点邻域中的K个邻近点拟合成一个平面或曲面,并将曲面该点处的法向量或曲率作为该点法矢量信息的估算值;也有些学者利用最小二乘法将相邻点局部进行平面拟合,得到P点的一个微分切平面,由此切平面得到该点的法向量估算值。如图4—图7所示,以上方法所得出的点的法线方向具有任意性,有些指向曲面内侧,有些指向外侧,对后续的法矢量的计算应用产生影响[9]。本文改进一种方法,通过三角网格顶点排序的方法将法线方向归一化,然后通过加权平均方法来估算单点的法向量。
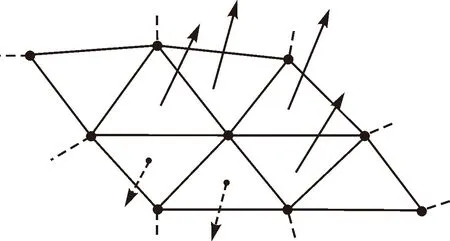
图4 三角面片法向量
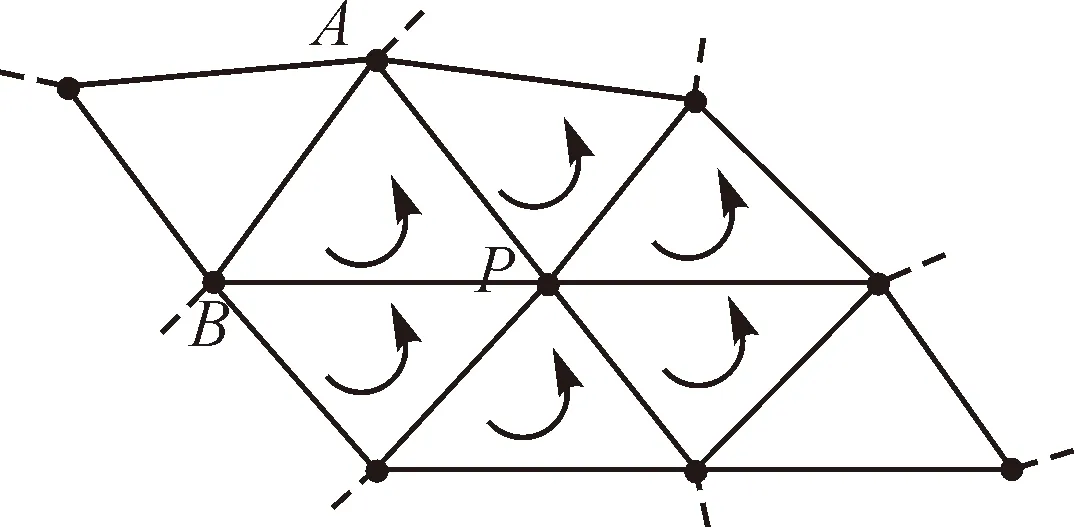
图5 三角面片顶点排序
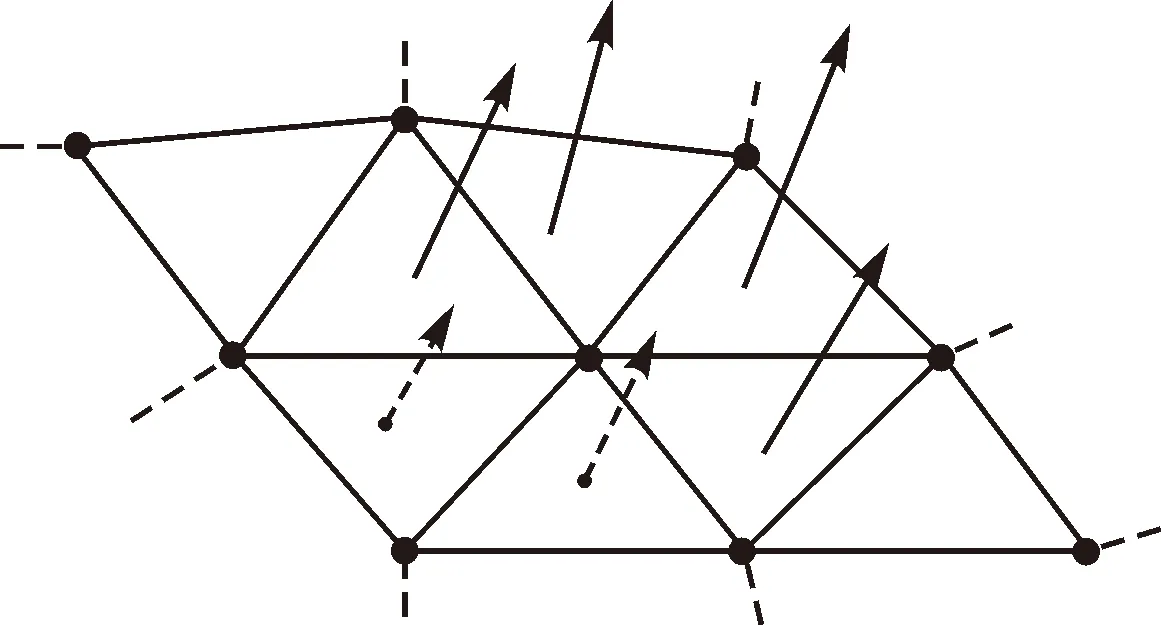
图6 调整后的三角面片法向量
2. 基于欧氏距离的局部二次曲面
局部地区点云的二次参数曲面表达形式如下
(1)
为了便于数学算法的表达与运算,将其转为矩阵表达式
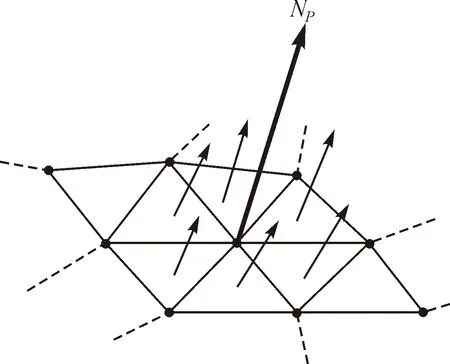
图7 单点法向量估算
(2)
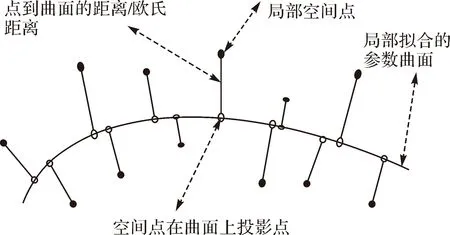
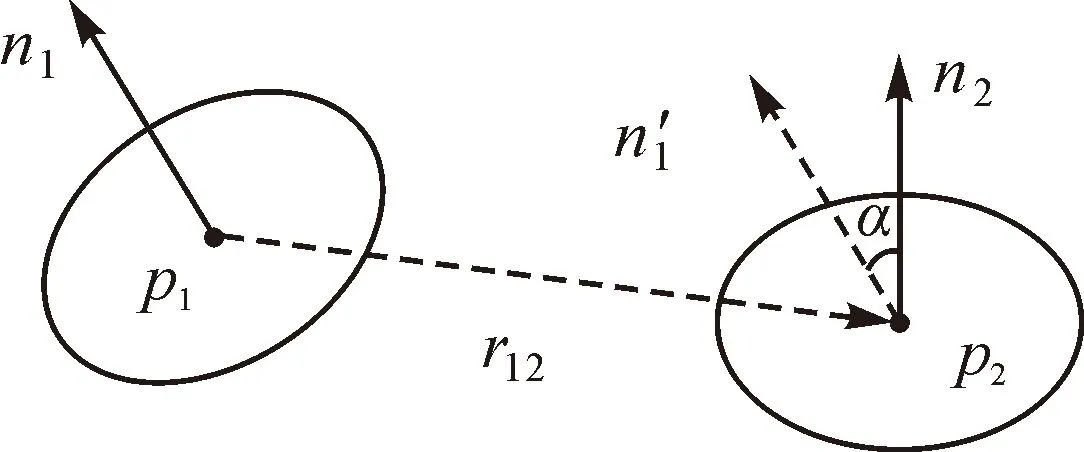
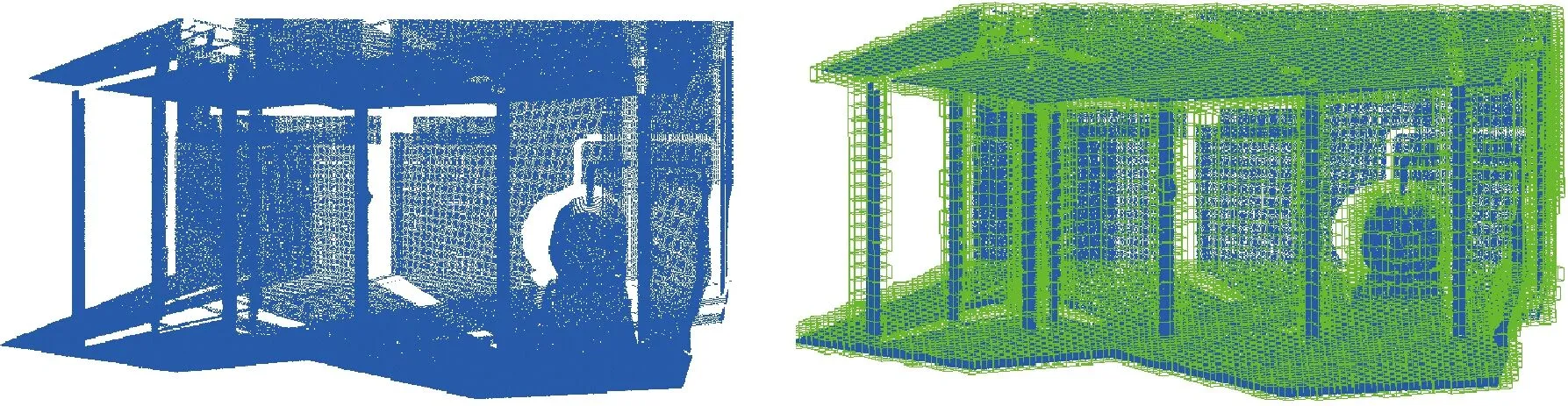
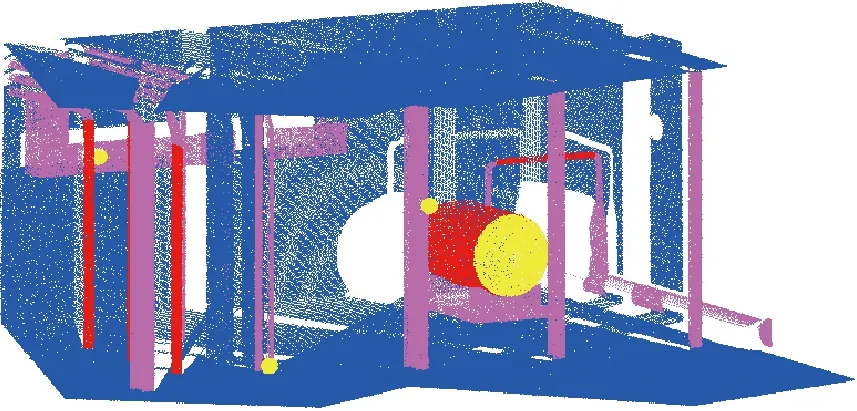
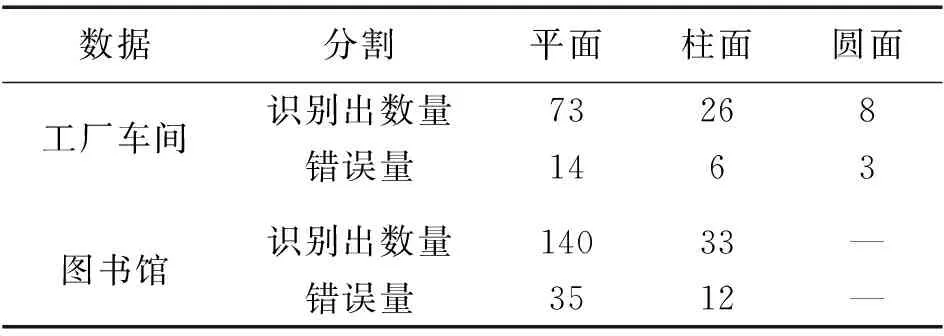
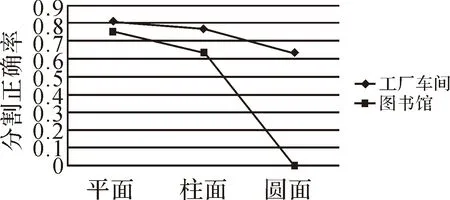
已知目标点P及其局部逼近的K个邻近点坐标(xi,yi,zi),0 (3) 根据以上公式,方程r(u,v)的分量即可表示为 x=WTa,y=WTb,z=WTc (4) 为了拟合出微分曲面S,对目标点P及其邻近点进行插值,使得已知坐标的K+1个点到该拟合曲面的欧氏距离的绝对值E取得最小值,数学表达方式如下 E=Z-MQ (5) (6) 根据最小二乘原理的思想,可将式(6)表达的空间距离取平方值,使得这K+1个点到拟合曲面S的欧氏距离的平方和最小,此时,得到基于欧氏距离最优的曲面表达式(如图8所示)。 图8 欧氏距离示意图 该方法是将目标点P及其邻近的总共K+1个点分别投影到曲面S上,也就是计算这些点到曲面S的欧氏距离,然后将投影线段长度求平方和,根据最小二乘法求平方和的最小值,取得最佳的曲面系数,即为基于欧氏距离的局部最优二次曲面。 1. 建立规则点云的约束条件 (1) 平面点云分割约束条件 平面点云分割约束条件为 (7) 1) 平面点云数据集中的点的法矢量应该具有一致的指向,考虑到系统误差及外界因素的影响,任何点与点之间法矢量的指向之间的夹角应该不超过一定的阈值。 2) 平面点云数据集中的所有点应该处在同一个平面模型中,并且一个点云集中点与其相邻点之间的距离不能超过一定的阈值。 3) 平面点的曲率理论值(Gauss曲率和平均曲率)等于零,在实际点云数据中应该趋近于零。 (2) 圆柱面点云分割约束条件 圆柱面点云分割的约束条件式如下 (8) 由圆柱体的空间数学模型表达式(8),反推圆柱面点云的特征,得出如下结论: 1) 圆柱体侧表面点云的法矢量指向在空间上垂直于圆柱体的中心线,将一个圆柱体侧面的法矢量平移到同一个起点时,它的法向量会形成一个以平移到的点为圆心,以法向量的单位长度为半径的单位圆。 2) 圆柱体侧表面点云的曲率值为常数。其Gauss曲率值等于零,最大主曲率值为圆柱体的半径的倒数,是一个常数,最小主曲率值为零。 (3) 球面点云分割约束条件 球面点云的分割约束条件如下 (9) 由式(9)反推球面点云数据的特征,得出如下结论: 1) 球体表面的点云的法矢量在空间指向上都经过同一个点,将球体表面所有点的法矢量都平移到球体球心处,它的法矢量会形成一个以法矢起点为球心,以法矢量长度为半径的单位球体。 2) 球面点云数据的曲率值为一个常数。其最大主曲率值等于最小主曲率值,且该常数等于该球体模型的半径的倒数。 2. 基于法矢量信息的平面点的识别与分割 经过基于邻近三角面片法矢量方向调整后的加权平均,得到了三维点的法向量,根据法向量特性,可以设置一定的限制条件来对平面点云进行分割。如图9所示,由平面的基本特征可知,平面点云必须满足以下两个条件: 1) 散乱点的法向量指向必须一致或在角度差一定的阈值区间内,即同向性。 2) 散乱点的局部拟合平面之间距离必须小于一定的阈值,即共面性。 图9 平面点云约束条件 3. 球面与柱面点的识别与分割 离散点的单个特征往往不足以用来区分一类曲面点云,需要将多方面的信息相结合来归纳曲面的特征。三维点云的曲率信息主要包含某点的最大主曲率、最小主曲率及高斯曲率。曲率的计算,采用基于欧氏距离拟合曲面方法进行。 结合球面与圆柱面点云的曲率特征,采用合理的识别与分割条件,将两类曲面分割步骤总结如下: 1) 由空间八叉树划分构建索引,并获取种子点的K个邻近点坐标。 2) 采用局部二次曲面的参数方程式来表示该K+1个点所表达的空间曲面,根据基于欧氏距离拟合的判断条件,将方程转变成K+1个点到曲面欧氏距离的平方和最小的误差方程,利用最小二乘原理,K+1个坐标点为已知条件,来进行平差计算,得到最优的拟合曲面方程式,并解算各种曲率值。 3) 统计分析点云数据的最大主曲率、最小主曲率及高斯曲率值,采用K均值聚类的方式,选定一个合适的种子点,对K个邻近点进行均值聚类分析,将曲率特征一致的点汇集到属性一致的集合中,反复执行聚类操作,直至划分结束(见表1)。 表1 两种规则曲面的曲率特征 1. 点云空间划分试验 采用徕卡地基激光扫描仪,获取某工厂车间的点云数据,对其进行空间八叉树结构划分,形成的空间网格结构如图10所示。根据空间八叉树网格结构划分算法流程,设定空间划分的终止阈值为50,然后将立方体内点云数量为空的网格删除掉,得到最精简的八叉树空间结构(如图11所示)。 图10 工厂车间点云的八叉树空间划分 采集校图书馆部分点云数据,进行空间划分试验,试验结果如图11所示。 图11 图书馆点云的八叉树空间划分 2. 规则点云分割试验 根据上述理论方法,采用相关数据进行试验,检验规则点云分割方法的可行性和试验效果。采用徕卡 Scanstation 2型激光扫描设备分别获取某个工厂车间的点云和某图书馆建筑的部分数据来进行试验。采用PointCloud软件对其进行数据处理,分别进行法矢量提取、规则点集分割与提取等处理,处理效果如图12—图16所示。 图12 点云法矢量 图13 工厂车间规则点集的分割和提取 图14 工厂车间规则点云提取后效果 图15 图书馆规则点集的点云的分割和提取 图16 图书馆规则点集提取后效果 对两组数据分割后的不同类型面片进行统计,找出各类型数据中识别出的点云集数量,并逐一进行人工对比判断,统计分割出现错误的点集,结果见表2,相应对象的点云分割正确率曲线如图17所示。 表2 两个点云分割结果对比 图17 不同类型点云分割正确率检验 对不同类型数据的分割结果进行分析可知,平面点云的分割效果较好,圆柱面和球面两种曲面点云的分割效果较差。纵向对比可以发现,图书馆数据的分割结果普遍比较差,这与数据的质量有关。图书馆数据采集中,由于其建筑结构复杂,激光扫描设备架站,以及外界人流与地物干扰等使得数据质量不高,而工厂车间数据较为规则、理想,结构简单。 以三维点云数据的分割为切入点,研究基于典型几何特征的激光点云分割方法,并进行了相应的试验。得到如下研究结论: 1) 研究了三维激光离散型点云数据的空间索引方法,针对激光点云数据的离散性、空间无拓扑、呈表面分布等特征,借鉴八叉树空间网格划分的形式,根据点云的密度选取合适的分割终止条件,将离散型数据有序组织可以有效提高数据的查找与调用,并用八进制数的编码对立方网格命名。利用八叉树的索引,对点云进行邻近值搜索,便于局部点云特征计算。 2) 采用加权平均的方法求解法矢量,该方法所估算的顶点法矢量精度可以满足要求,可以作为平面点云分割的法矢量依据,以局部点到拟合曲面的欧氏距离平方和最小为拟合条件,平差得出的曲面最能反映局部的曲面形状,所得出的曲率值效果最好。 3) 针对常见的几种面片形式,提出了基于几何特征的不同类型点云识别与分割的约束条件。以徕卡Scanstation 2型扫描仪获取的点云数据为试验对象,证明了法矢量和曲率信息在数据分割中的重要性。 [1]詹庆明,周新刚,肖映辉, 等.从激光点云中提取古建筑线性和圆形特征的比较[J].武汉大学学报(信息科学版),2011,31(6):674-677,682. [2]魏征,杨必胜,李清泉.车载激光扫描点云中建筑物边界的快速提取[J].遥感学报,2012,16(2):286-296. [3]李必军,方志祥,任娟.从激光扫描数据中进行建筑物特征提取研究[J].武汉大学学报(信息科学版),2003,28(1):65-70. [4]邓非,张祖勋,张剑清.利用激光扫描和数码相机进行古建筑三维重建研究[J].测绘科学,2007,32(2):29-30. [5]莫堃,尹周平.基于3D活动轮廓模型的缺陷点云分割方法[J].华中科技大学学报(自然科学版),2011,39(1):82-85. [6]李清泉,李德仁.八叉树的三维行程编码[J].武汉测绘科技大学学报,1997,22(2):12-16. [7]权毓舒,何明一.基于三维点云数据的线性八叉树编码压缩算法[J].计算机应用研究,2005(8):70-71,129. [8]杨客,张志毅,董艳.基于自适应八叉树分割点云的表面模型重建[J].计算机应用与软件,2013,30(6):83-87. [9]姜寿山,Eberhard P.多边形和多面体顶点法矢的数值估计[J].计算机辅助设计与图形学学报,2002,14(8):763-767. [10]张量,王敏.基于k邻域离散扩张的点云数据分割[J].软件导刊,2009,8(12):7-9. The Segmentation of Regular Laser Point Cloud Based on Geometry Feature FANG Jun,LI Chaokui,ZHANG Xinchang,ZHANG Qiang,LIAO Mengguang,BU Pu 2015-10-29; 2016-06-24 国家自然科学基金(41271390;41571374);国土资源部公益性行业科研专项(201511079-04);空间信息智能感知与服务深圳市重点实验室开放基金资助(2015C11508);特殊环境道路工程湖南省重点实验室开放基金(kfj150502) 方军(1985—),男,博士,研究方向为遥感信息提取与三维GIS应用。 李朝奎。E-mail:616059644@qq.com P208 B 0494-0911(2016)08-0047-06 引文格式:方军,李朝奎,张新长,等.顾及几何特征的规则激光点云分割方法[J].测绘通报,2016(8):47-52.DOI:10.13474/j.cnki.11-2246.2016.0254.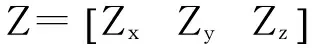
三、特征点云的分割


四、试 验





五、结 论

