参考框架的精化对GPS时间序列的影响与分析
梁洪宝,申 星,刘雪龙
(中国地震局第一监测中心,天津 300180)
参考框架的精化对GPS时间序列的影响与分析
梁洪宝,申星,刘雪龙
(中国地震局第一监测中心,天津 300180)
GPS时间序列的精化解算受参考框架影响显著,本文基于ITRF2008参考框架分别设计了4种参考框架方案,通过对(112°E—124°E,30°N—39°N)范围内20个GPS测站2010年6月—2015年6月数据进行处理与统计分析,取得了如下认识:①在研究区域内增加少量连续GPS台站与全球IGS站一起组成的全球精化参考框架,可以保证解算结果的离散度稳定,并且可以抑制测站周年变化的振幅,体现出了动态参考框架的优势;②区域参考框架能够有效吸收共模误差,减弱全球刚性运动和周期性运动的影响,解算结果的精度高于全球框架,NEU单日解坐标重复性分别平均提高了13.7%、24.1%和38.0%,另外,区域参考框架N分量可能受温度变化的影响较为明显;③测站单日解坐标重复性和坐标精度均表现出季节性变化特征,每年7、8月较低。
动态参考框架;GPS时间序列;坐标重复性;季节性变化
连续GPS站的快速发展,已为开展地震预报、国防建设、大地测量和地学研究等工作发挥了显著作用[1-3],随着连续GPS站的实时观测,为了保证前后测绘成果的连续性和延续性,必须将GPS结果归算至统一框架下,因此,参考框架的可靠性已成为GPS精化计算中关键问题。目前,GPS计算中一般采用IGS组织于2010年发布的ITRF2008框架(2012年10月进行了更新),该框架是由框架点在参考历元2005.0时的坐标和速度来定义的,一旦框架点的坐标和速度确定下来,通常按照线性模型来推估待转换历元的坐标[4],但实际上,由于框架点会受到板块运动等因素的影响,并非表现为严格的线性运动特征,按照线性模型推算至待转换历元的坐标将会带有误差,并且误差会随时间的增大而增大,这种参考框架的现势性不足必将扭曲连续GPS结果[5]。在框架点的选取方面,通常按照连续性、高精度、多种解、平衡性、稳定性和精度一致性等原则选择均匀选取[6],并且兼顾计算区域内部及周边区域[7],而我国大陆及周边IGS站的观测不连续和停用,导致中国大陆及周边核心框架点减少,致使平差过程中全球控制网对我国区域GPS站的约束力大大降低。我国于“十一五”期间启动了国家重大科技基础设施项目 “中国大陆构造环境监测网络”(以下简称“陆态网络”),其中改造和新建了约260个连续GPS站,并于2010年下半年陆续开始观测,至今已连续观测近5年,为增强ITRF框架的动态性和满足框架点的选取原则等方面提供了可能。因此,本文基于陆态网络连续GPS站,通过4种参考框架方案下GPS时间序列精密解算与结果统计,分析参考框架的精化对于GPS时间序列的重要性。
一、数据处理方案
鉴于中国东部相对形变量较小,约为2 mm/a[8],为了凸显其相对形变信息,本文选择(112°E—124°E,30°N—39°N)范围内较为稳定的20个连续GPS站为研究对象,测站分布如图1所示,观测数据时间从2010年6月—2015年6月,数据处理平台采用GAMIT/GLOBK 10.50软件,具体数据处理方案如下:
方案1:IGS解算方案。利用GAMIT10.50软件对研究区域连续GPS站和周边10个IGS站(BJFS、SHAO、WUHN、CHAN、LHAZ、TNML、SUWN、TSKB、ULAB、URUM)进行单日解解算,IGS站坐标约束为0.050、0.050和0.100 m,连续GPS站坐标约束为30、30和80 m;然后与SOPAC全球7个H文件绑定,选取IGS中心平差解算中采用的所有核心站作为框架点;最后利用GLOBK软件进行网平差。
方案2:与方案1不同的是从所有的核心站中按照连续性、高精度、多种解、平衡性、稳定性和精度一致性等原则选择91个均匀分布的测站作为框架点,站点分布如图2所示。
方案3:在方案2的基础上,对连续GPS站进行时间序列分析,利用式(1)[9]获取其精密坐标和速率,同样按照连续性、高精度、多种解、平衡性、稳定性和精度一致性等原则选择均匀分布的7个陆态网络连续GPS站(HELY、SDRC、TAIN、ZHNZ、AHBB、AHAQ、JSNT)作为框架点。

图1 区域GPS站分布

图2 全球框架GPS站分布

(1)
式中,a为初始位置;b为速率;c、d、e和f分别为年、半年周期项系数;g为偏移;h为震后速率变化(可能存在)。
方案4:在方案3获取的陆态网络连续GPS站的精密坐标和速率基础上,利用GAMIT 10.50软件对研究区域内2个IGS站(WUHN和SHAO)站和18个陆态网络连续GPS站进行单日解解算,坐标约束均为0.050、0.050和0.100 m,以1个IGS站(WUHN)和7个陆态网络连续GPS站(HELY、SDRC、TAIN、ZHNZ、AHBB、AHAQ、JSNT)作为框架点。
二、结果分析与讨论
为了分析不同参考框架对GPS时间序列的影响,本文只对研究区域内12个非框架点(图1中黑色站点)进行分析。
1. GPS时间序列坐标重复性分析
衡量GPS坐标时间序列解算精度的指标通常采用单日解坐标重复性,其计算如式(2)和式(3)所示,其值越大,表示GPS时间序列坐标重复性越小,坐标离散度越大,解算结果较差,其值越小,表示GPS时间序列坐标重复性越大,坐标离散度越小,解算结果较好。
(2)
(3)
式中,n为观测历元总数;ci为观测值;σi为观测值的误差。
为了定量分析不同数据处理方案下GPS时间序列的差异,本文将不同方案下的单日解解坐标重复性差异定义为式(4),表示为方案j下单日解坐标重复性相对方案i的变化度,若dif_wrmsij为正值,表明方案j解算结果优于方案i,若dif_wrmsij为负值,表明方案i解算结果优于方案j。
(4)
本文获取了4种计算方案下研究区域内12个GPS站的单日坐标重复性,结果如图3所示,相对方案1,方案2的三分量坐标重复性略微有所提高,平均提高了10.7%、4.2%和1.1%,说明了全球框架点的合理选取及其测站分布的均匀性均对GPS序列产生一定的影响;相对方案2,方案3的水平分量坐标重复性有了明显提高,平均提高了20.2%和26.6%,垂向提高幅度不大,平均提高了5.0%,说明了全球参考框架的动态性对在GPS解算中具有重要作用;相对方案3,方案4的三分量坐标重复性均有明显提高,平均提高了13.7%、24.1%和38.0%,说明了区域参考框架要优于全球参考框架。
另外,为了分析4种计算方案对GPS时间序列的动态影响,本文对4种计算方案下每个测站的每月的单日坐标重复性进行统计。本文以测站单日解坐标重复性结果与平均结果相近的HECX站为例进行说明,结果如图4所示,为了凸显其动态变化特征,利用高斯加权函数平滑方法对其进行滤波,图中曲线即为滤波结果。从结果中可以看出,4种方案坐标重复性均表现出季节性变化的特征,每年7、8月离散度最大;方案1和方案2水平方向离散度有逐渐增大的趋势,主要原因是IERS组织利用后续GPS数据对ITRF2008框架进行维护,推出的IGb08数据截止时间仅仅是2012年10月,因此,对于后续的GPS计算,ITRF2008框架已经不能满足现势性的需求;方案3增加了同步连续GPS站点为框架点,使这种离散度偏大的趋势得到了一定程度的控制;方案4的框架点全部为区域同步连续GPS站点,基本消除了这种现象。由此可见,动态参考框架对于高精度的GPS网平差具有关键作用。
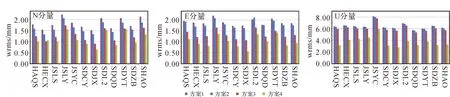
图3 单日解坐标重复性

图4 HECX站每月单日解坐标重复性(自上而下依次是方案1、方案2、方案3和方案4)
2. GPS坐标值及其精度的比较
4种计算方案下GPS整体解算精度的比较已通过上节单日解坐标重复性得出动态框架优于非动态框架、区域框架优于全球框架,而在实际应用中,需要同时考虑解算结果的两个方面——坐标值及其误差,本文分别就不同方案间的坐标值及其误差的差异进行了比较。
在坐标值方面,由于方案4的坐标重复性最大且动态变化稳定,因此,以方案4为基准,方案1、方案2和方案3分别与其坐标值求差处理,HECX站三分量之差如图5所示,图中曲线为高斯加权平滑滤波结果。从结果可以看出,相对方案4而言,3种方案在水平方向均剔除了部分系统性运动和周期运动,在垂向仅剔除了周期运动;方案1和方案2的坐标差异离散度大于方案3,且存在逐渐偏大的趋势。

图5 HECX站坐标值比较(自上而下依次是方案1、方案2、方案3与方案4之差)
在坐标误差方面,本文对4种方案坐标误差进行了统计,除去方案4垂向精度低于前3种方案外,从整体上看,方案1和方案2相近,方案3和方案4相近,但方案3和方案4的精度要高于方案1和方案2。为了分析其误差的动态特征,本文列出了HECX站4种方案的三分量坐标误差,结果如图6所示,图中曲线为高斯加权平滑滤波结果。从图中可以看出,从每一种方案来看,坐标分量误差呈现季节变化的特征,在每年7、8月精度最低;方案1和方案2水平分量误差有逐渐增大的趋势,方案3和方案4误差变化较为平稳。

图6 HECX站坐标误差比较(自上而下依次是方案1、方案2、方案3和方案4)
3. GPS坐标时间序列频谱特征的比较
研究表明,连续GPS站存在周期性变化的特征,通过前面的统计分析,方案1将所有的稳固测站作为框架点,而未进行精细选取,使得单日解坐标重复性和坐标精度均小于方案2,为了研究参考框架对连续GPS站的周期运动特征的影响,本文采用CATS软件[10]仅对经过框架点精细选取的方案2、方案3和方案4的坐标时间序列进行功率谱密度分析,12个站的结果如图7所示。功率谱密度值越大,说明其周期振幅越大,功率谱密度值越小,周期振幅越小,为了凸显GPS测站较短周期变化,本文仅取其最大周期为3a。

图7 SDJX站频谱特征
框架的不同会造成连续GPS周期性信号发生变化,本文对结果进行了统计。结果表明,相对方案2,方案3N分量周年振幅变化较小,E、U分量周年振幅均小于方案2,且E分量的相对减小幅度较大;相对方案2或方案3,方案4的U分量测站周年振幅均小于方案2或方案3,N分量和E分量分别有42%(5个)和75%(9个)的测站周年振幅小于方案2或方案3,但在周年振幅大于方案2或方案3的测站中,方案2或方案3下测站的半周年特征较为明显,且振幅幅度与周年振幅相近。
三、结束语
本文分别设计了IGS解算方案、全球参考框架、全球动态参考框架和区域动态参考框架4种数据处理方案,通过形变量较小的区域(112°E—124°E,30°N—39°N)内20个连续GPS站的精密解算,然后分别通过单日解坐标重复性、坐标值差异及误差比较和测站频谱分析3方面对12个非框架点的时间序列进行统计分析,得出以下结论:
1) 框架点选取原则。框架点的选取在遵循连续性、高精度、多种解、平衡性、稳定性和精度一致性等原则的基础上还应遵循均匀分布和兼顾计算区域内部及周边的原则,方案2单日解坐标重复性大于方案1就说明了这一点。
2) 动态框架优于非动态框架。方案2单日解坐标重复性存在逐渐增大的趋势,方案3中这种逐渐增大的趋势得到了一定程度的控制且单日解坐标重复性大于方案2;在坐标精度方面,方案3N、E、U平均坐标精度也分别高于方案2 0.49、0.60和0.18mm;相对方案2,方案3能够有效抑制部分测站周年振幅的变化幅度。可见,动态框架在GPS网平差中具有较强的稳定约束力。
3) 区域框架优于全球框架。方案4坐标重复性较为稳定且明显高于方案3;方案4能够在一定程度上减弱地壳刚性运动和周期运动的影响,从全球板块运动角度讲,系统性运动主要是全球板块的刚性运动引起的,周期性运动主要是由全球地表物质负荷引起地心的周期性运动通过转换参数传递到地球表面引起的[11],对于区域地壳形变监测而言,区域内站间存在时空相关的共性误差,在平差和坐标转换中可以完成站点的滤波处理;区域框架的不足可能是受温度变化的影响较为明显[12],如方案4中多数测站N分量周年振幅较方案2或方案3变大,而E、U分量较方案2或方案3减小,这与温度随纬度的空间变化特征相吻合,研究也表明温度因素对GPS定位存在影响[13],但该因素对GPS定位及其参考框架的影响规律还需进一步研究。
4) 单日解坐标重复性和坐标误差变化存在季节性变化的特征,在每年7、8月,坐标离散度和坐标误差均较大,这可能受存在季节性变化的多种因素的影响,为保证测绘成果的质量,对于流动GPS观测,可避免在该时间段内实施。
致谢:感谢美国MIT提供的GAMIT/GLOBK软件和英国国家海洋中心SimonD.P.Williams教授提供的CATS软件,以及武汉大学邓连生博士对本软件使用中的耐心指导。
[1]李强,游新兆,杨少敏,等.中国大陆构造变形高精度大密度GPS监测—现今速度场[J].中国科学D辑:地球科学,2012,42(5):629-632.
[2]WU Y Q,JIANG Z S,WANG M, et al. Preliminary Results of the Co-seismic Displacement and Pre-seismic Strain Accumulation of the Lushan MS7.0 Earthquake Reflected by the GPS Surveying[J]. Chinese Science Bulltin 2013, 58(28-29). DOI:10.1007/s11434-013-5998-5
[3]梁洪宝,刘志广,黄立人,等.非构造形变对中国大陆GNSS基准站垂向周期运动的影响[J].大地测量与地球动力学,2015,35(4):589-593.
[4]成英燕.ITRF2008框架简介[J].大地测量与地球动力学,2012,32(1):47-50
[5]宁津生,王华,程鹏飞,等.2000国家大地坐标系统框架体系建设及其发展[J].武汉大学学报(信息科学版),2015,40(5):569-573.
[6]秘金钟,蒋志浩,张鹏,等.IGS 跟踪站与国内跟踪站联合处理的框架点选择研究[J]. 武汉大学学报(信息科学版),2007,32(8):704-706.
[7]丁晓光,占伟,王紫燕,等.不同参考框架对区域连续GPS数据解算的影响[J].大地测量与地球动力学,2014,34(2):161-166.
[8]杨国华,杨博,陈欣,等.华北现今三维形变场空间变化的基本特征[J].武汉大学学(信息科学版),2013,38(1):31-35.
[9]NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D].San Diego:University of California,2002.
[10]WILLIAMS S D P. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS Solution, 2008(12): 147-153.
[11]DONG D N, QU W J, FANG P, et al. Non-linearity of Geocentre Motion and Its Impact on the Origin of the Tterrestrial Reference Frame[J].Geophysical Journal International,2014,198(2):1071-1080.
[12]BLEWITT G, KREEMER C, HAMMOND W C, et al. Terrestrial Reference Frame NA12 for Crustal Deformation Studies in North America[J].Journal of Geodynamics,2013(72):11-24.
[13]王洪栋.气象模型偏差对GPS定位结果的影响[D].北京:中国地震局地质研究所,2015.
Influence and Analysis of the Refinement of Reference Frame for GPS Time Series
LIANG Hongbao,SHEN Xing,LIU Xuelong
10.13474/j.cnki.11-2246.2016.0247.
2016-01-29;
2016-03-29
地震科技星火计划(XH15060Y);科技部基础性工作专项(2015FY210400);中国地震局青年震情跟踪课题(2015010211)
梁洪宝(1984—),男,硕士,工程师,主要从事高精度GNSS数据处理与形变分析。E-mail:lhb131421@126.com
P228
B
0494-0911(2016)08-0015-05
引文格式:梁洪宝,申星,刘雪龙.参考框架的精化对GPS时间序列的影响与分析[J].测绘通报,2016(8):15-19.

