高中数学教学中导数与积分的应用
王淑云(吉林省白城市第十四中学)
高中数学教学中导数与积分的应用
王淑云
(吉林省白城市第十四中学)
随着我国教育的不断改革,高中数学的内容也更加注重实用性与操作性。高中数学不仅是初中数学的深入,也是大学数学的重要衔接。导数与积分作为高中数学教学的重要内容,是学生熟练掌握高中数学知识要点、提升解题能力的重要方式。主要讨论高中数学导数与积分在解题中的应用,以此阐述导数与积分在高中数学中的地位和意义。
高中数学;导数;积分
高中导数是函数的重要内容和要点,导数需要运用大量的公式进行运算,以此帮助学生更好地掌握较为抽象的函数。积分也是函数中的一个重要内容。利用积分,学生可以更好地解决三角函数难题。导数和积分都能将函数化繁为简,帮助学生更好地掌握相关函数的解题思路与技巧。
一、导数在高中数学教学中的应用
导数在函数最值、极值和取值范围中的应用。
已知函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1,求:
(1)若函数f(x)在x=-2处有极值,求f(x)的表达式。
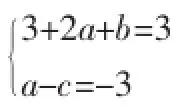
因为y=f(x)在x=-2上有极值,所以f(-2)=0,所以-4a+b=-12③
从①②③可得,a=2,b=-4,c=5,所以f(x)的表达式为f(x)= x3+2x2-4x+5。
(2)在(1)的条件下,求函数y=f(x)在[-3,1]的最大值。
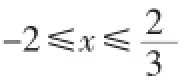
(3)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围。
解:因为函数y=f(x)在区间[-2,1]上单调递增,又因为f′(x)= 3x2+2ax+b,并由①得出2a+b=0。根据题意所得f′(x)在[-2,1]上恒有f′(x)≥0,即3x2-bx+b≥0。由此可以得出:
二、积分在高中数学中的应用
配方法是积分中最为常用的一种方式,配方法的重点主要在于“配”与“凑”这两点上。其使用的原理是根据二项完全平方公式(a+b)2=a2+2ab+b2。由该项公式可以推导出各种所需要的平方公式,如:a2+b2=(a+b)2-2ab,或者是a2+ab+b2=(a+b)2-ab等等。
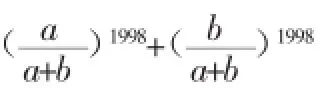
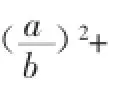

这道题的关键主要是通过配方,简化了所求的表达式,并巧用了1的立方虚根,活用ω的性质,通过一系列的换算变形后。由此,了解各方程式并进行换算则是积分解决函数问题的重要技巧之一。
三、导数与微积分在高中数学中的应用
四、结论
导数和积分有着丰富的背景,并得到了广泛的应用,掌握它们之间的内在关系,教师可以互用导数和积分,让学生掌握不同函数问题中不同的解决方式。如教师可以利用切线的斜率和瞬时速度让学生明白导数的改变和几何性质。在学习积分时,也可以利用导数中的极限思维,在某个局部的小范围内进行“以不变代变”或者是“以直代曲”,让学生掌握积分的概念与解题方式。只有充分掌握导数与积分的概念和函数性质,学生才能更好地运用其解决相关的函数问题,才能更好地解决高中函数问题。
[1]陈剑.高中导数与积分教学策略分析[J].数学学习与研究,2011(15):18.
[2]王湘平.微积分在高中数学解题中的应用[J].才智,2013(5):37-38.
·编辑张珍珍

