构建几何模型求三角形面积的最大值
康峰
(山东省新泰市实验中学)
构建几何模型求三角形面积的最大值
康峰
(山东省新泰市实验中学)
一、问题展示,导入课题
师:同学们,近几年各地的中考题中经常涉及一类求面积最大值的问题。
(课件展示几个涉及求面积最大值的中考题)
师:同学们在解决这类题目时,往往遇到的困难是解题思路不清晰或者是解题方法复杂。通过这节课的学习,希望同学们能够明确这类题目的解题思路,探究出解决问题的简单方法。
(板书课题:构建几何模型求三角形面积的最大值)
师:首先请同学们完成下面的一个基础题目。
二、问题探究,构建模型
(课件展示一个基础题目,让学生自主完成)
已知:点A(0,2),B(4,0),C(3,3),求△ABC的面积。

(教师巡视,发现学生通常采用两种方法求解:一是过点C作CD⊥y轴于D,利用S△ABC=S梯形OBCD-S△ADC-S△ABO,一是过点C作CE⊥x轴于E,利用S△ABC=S梯形AOEC+S△CEB-S△ABO)
(让学生相互交流作法)
师:找一位同学回答一下你的做法。
生1:过点C作CD⊥y轴于D,S△ABC=S梯形OBCD-S△ADC-S△ABO=5。
师:回答得非常好!还有没有其他做法?哪位同学说一下?
生2:过点C作CE⊥x轴于E,S△ABC=S梯形AOEC+S△CEB-S△ABO=5。
师:很好,刚才两位同学都是利用了“和差法”来求三角形ABC的面积。我们还能不能找到其他做法呢?
(展示课件)
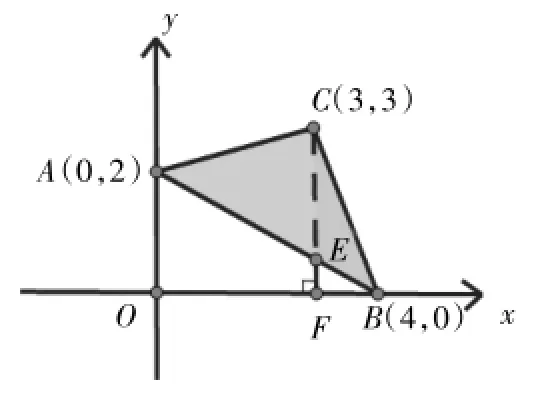
师:如果过点C作CF⊥x轴于F,交AB于点E,那么S△ABC= S△AEC+S△CEB.同学们想一想,△AEC与△CEB有什么关系?
生3:可以把CE看做它们共同的底。
师:很好,那么△ACE中CE边上的高可以用谁来表示?△BCE中CE边上的高可以用谁来表示?
生4:△ACE中CE边上的高可以用OF表示,△BCE中CE边上的高可以用BF来表示.
师:我们知道,解决数学问题时,用整体思想有时可以简化一些解题步骤。在这里,我们可以把OF和FB相加作为一个整体来计算,这样我们就可以得到求三角形ABC面积的一种新方法了。
师:同学们,你能用这种方法算出三角形ABC的面积吗?试一试,交流一下你们的做法。
(教师巡视引导)
师:我找一名同学说一下是怎样算出三角形ABC面积的?
师:非常好!下面我们利用这种求三角形面积的方法来解决一类求面积最大值的问题。
三、应用模型,解决问题
(展示课件)
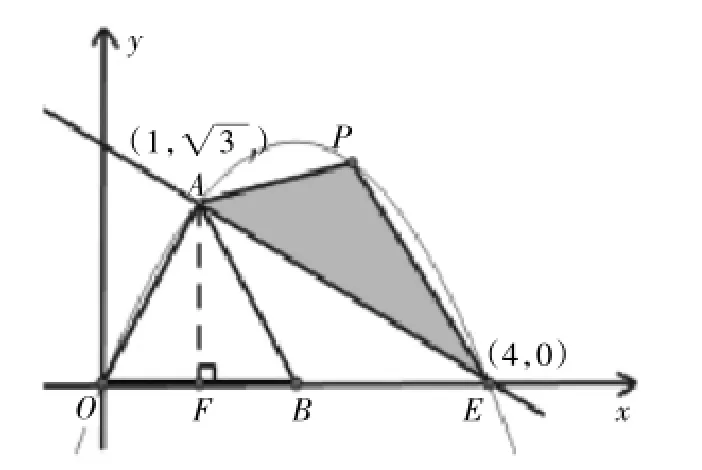
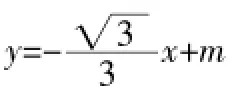
(1)求点E的坐标;
(2)求过A、O、E三点的抛物线的解析式;
(3)若点P是(2)中求出的抛物线AE段上一动点,设△APE的面积是S,求S的最大值.
师:请同学们先完成本题的前两问。
(2分钟后投影展示生6的答案)制约因素得到满足时,该因素往往成为主导因素。从两者的概念来说,主导因素和限制性因素都是相对于农业生产所在的地区来说,而不是对于某种农作物来说,例如,宁夏平原发展水稻种植的主导因素是水源,而不能说水稻种植业的主导因素是水源,宁夏平原地形平坦,冲积平原土壤肥沃,夏季光热充足,但降水量少,所以其能发展水稻的主导因素是水源。如果要问宁夏大面积发展水稻种植的限制性因素是什么?这时应该回答是降水。
在确定主导因素和限制性因素时,除了考虑所在地区的特点外,也要综合考虑所发展事物本身的特点。例如,珠江三角洲的基塘农业,是在特有的地形气候条件下形成的,当地地势低洼,排水不畅,特别是一下雨容易积水,当地人因地制宜,挖泥成塘,堆泥为基,以改造当地地形为突破口,形成了基塘农业,低洼的地势成为基塘农业发展的突破口,因此地形是它的主导因素。但从另一方面来说,地形却是发展其他农业生产的限制性因素,如,珠江三角洲多水患的特点,排水不良,这就成为水稻生产的限制性因素。
因此,我们在做主导因素与限制性因素分析时,一定要分清所属的地区特点和所面对的生产活动特点。分析那些因素是优势条件还是劣势条件,一般优势条件就从主导因素方面去分析,劣势条件从限制性因素方面去分析。所以说,让学生掌握“主导因素”与“限制性因素”是学会区位评价的关键,建议我们的课本编写者在教材中应该增加这两个基本概念。
[1]赵志强.因素分析法在高中地理教学中的应用研究[D].东北师范大学,2008.
[2]商幸丰.浅议地理教学方法设计中的几个问题[J].中学地理教学参考,1993.
·编辑张珍珍

