活学巧用导数的几何意义
汪灶华(江西省婺源县紫阳中学)
活学巧用导数的几何意义
汪灶华
(江西省婺源县紫阳中学)
作为一名刚带完2015届高考的一线老师,我总想为来年高考备战的老师和同学们留下一点自己的感触.把今年试题与往年试题(导数的几何意义客观部分)进行仔细对比,然后又翻看了一下这几年的考试大纲,最终发现一个规律:在全国上下把素质教育放在第一位的今天,命题老师把实际生活中一些常见图形放到试卷中来,纵观前几年江西高考数学题(尤其是理科),表面上是考查学生对导数的实际意义掌握情况,而实际上还综合考查了学生对数学的探究能力和知识应用能力.现在对导数的实际意义的考查题目分为两个层次:第一层次,给出原函数f(x)及其导函数f′(x)中的一个函数图象,让你推测没有给出的那个函数图象,或者求曲线的切线方程,应该说这一层次题目考查力度停留在表面,难度较小;第二层次,提供给你一定的生活背景图(看上去常见,也挺规则的),要求你观察并且推出某些量(面积、体积等)的变化多少及快慢问题,这一类问题没有给我们任何图象,而且大部分图象不规则,一般都会放在选择题的倒数三题里,难度自然就有所提高,倘若能把这两层次题都弄懂,我相信考试应该会很少在导数的几何意义上碰壁了.
第一层次:活学导数的几何意义研究函数图象的切线方程
导数反映了函数的变化率,从图形上来看,表现为切线的斜率,如:导数f′(x0)表示曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.如果导数为负,则切线的斜率为负,切线呈现为下降趋势,曲线在该点附近也是下降趋势,函数单调减.如果导数为正,函数单调增.而求切线方程可以分两步:第一步求出函数在点x0处的变化率,得到曲线在点P(x0,f(x0))处的切线的斜率;第二步根据直线方程的点斜式写出切线方程即y-f(x0)=f′(x0)(x-x0).
【例1】原题(选修2-2第二十九页练习第一题)改编如图是导函数y=f′(x)的图象,那么函数f(x)在下面哪个区间是减函数()
A.(x1,x3)B.(x2,x4)C.(x4,x6)D.(x5,x6)

【解析】函数的单调递减区间就是其导函数小于零的区间,故选B.
第二层次:巧用导数的几何意义研究函数图象的变化趋势
利用导数的几何意义研究函数图象的变化趋势,是对导数几何意义运用的进一步加深,这一层次题出现在高考中不是要求考生花大量笔墨去算,而是要理解函数值的增加或减小快慢情况对切线斜率的影响,倘若计算运算量将会很大.这一层面题目一般选项都会出现图象,你可以计算出精确值,也可以通过考虑图象的性质,对选项进行筛选估计等即可得出答案,具体见例题:
【例2】(2013年江西高考理科)如图,半径为1的半圆O与等边三角形ABC夹在两平行线,l1,l2之间l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点,设弧FG的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2,则函数y=f(x)的图象大致是()
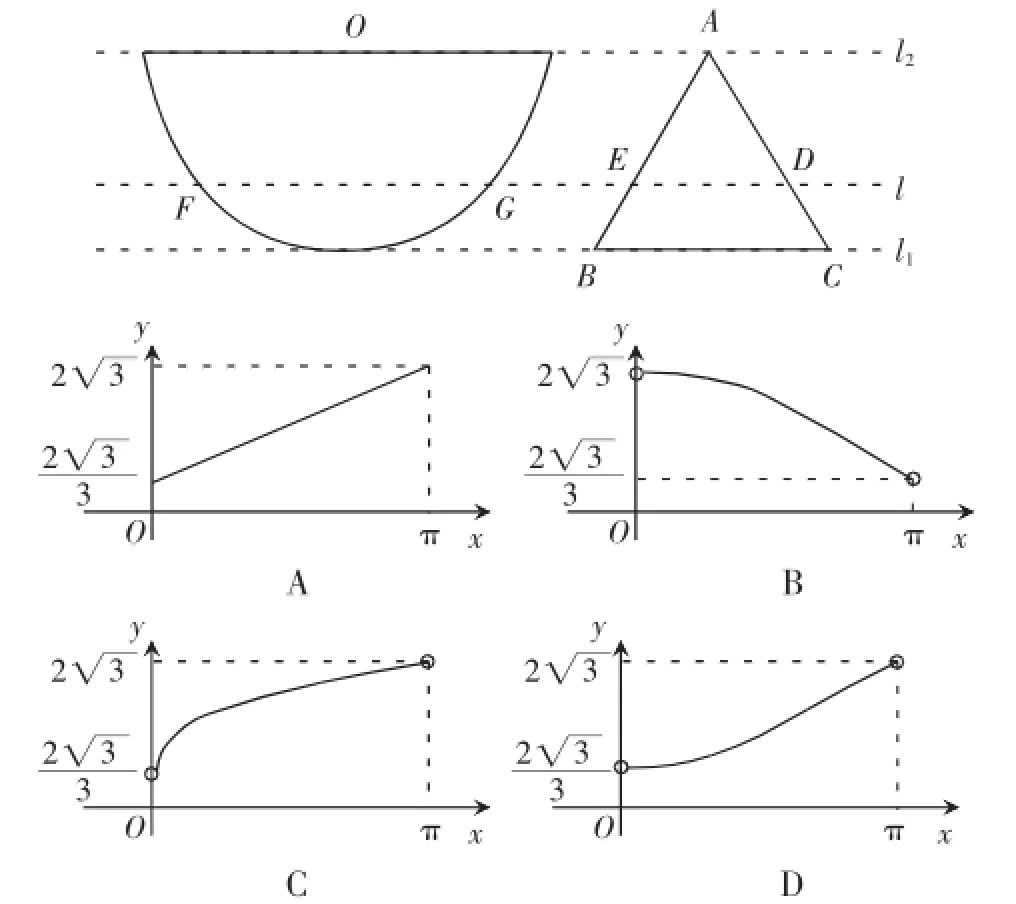
【解析】本题考查函数的图象,扇形弧长,三角函数,以及数形结合的数学思想.当x逐渐增大时,y也逐渐增大,故y随x的增大而增大.故先排除B项.
【解法2】直接观察发现x量逐渐减少,而y增量没有改变,其实也就相当于告诉我们当x增量一直保持不变时,y增量会逐渐增大,因此图象看上去会越来越陡,故选择D.
·编辑鲁翠红

