含裂纹弯头的极限载荷试验研究

马凤兰，郭茶秀（.郑州市安全生产教育中心，河南郑州　450006；2.郑州大学化工与能源学院热能系统节能技术与装备教育部工程研究中心，河南郑州　45000）

含裂纹弯头的极限载荷试验研究

马凤兰1，郭茶秀2*
（1.郑州市安全生产教育中心，河南郑州450006；2.郑州大学化工与能源学院热能系统节能技术与装备教育部工程研究中心，河南郑州450001）

摘要：为了试验研究含面型缺陷弯头的极限承载能力，设计并进行了8个无缝弯头试样在内压和张开模式的平面内弯矩试验，对其中的无缺陷和有缺陷弯头记录了相应的压力—体积变化曲线、压力—裂纹嘴张开位移曲线、力—加载点位移曲线或力—裂纹嘴张开位移曲线，并对弯头截面的椭圆度和弯矩载荷之间的关系进行了分析。根据测试得到的曲线确定了这8个弯头试件的试验塑性极限载荷，并将试验结果与有关理论进行了分析比较。

关键词：弯头；极限载荷；裂纹

0　引言

弯头是石油化工行业大量采用的管道元件，由于几何形状复杂，且受到的载荷除了内压外还有弯矩和扭矩等载荷，所以管线中弯头上承受的应力往往比直管大，也就容易在弯头上形成裂纹、拉伤、局部凹坑等缺陷，且以纵向裂纹居多。弯头一般采用韧性较好的材料制造，其失效模式通常是由极限载荷控制的塑性破坏，所以为了对含缺陷弯头进行安全评定，其中的塑性极限载荷是一个必不可少的重要参量。国内外研究人员对无缺陷弯管极限载荷的研究开展了大量工作。例如，Calladine等［1-2］基于小变形理论对内压或弯矩载荷作用下弯头的塑性承载能力进行了相关探索和研究。而段志祥等［3-4］采用有限元方法研究内压或弯矩载荷作用（闭合模式）下弯头的极限载荷。弯头含表面裂纹或穿透裂纹，都会明显地降低其承载能力。王辰等［5］对含纵向或环向穿透裂纹弯头的极限载荷进行了有限元分析。试验研究含裂纹弯头塑性极限载荷的并不多，Kastner等［6］分别对弯头外拱线和几何中性线处含穿透裂纹时的塑性极限压力进行了试验研究，Griffith［7］试验研究了四个几何中性线外含纵向穿透裂纹弯头和二个周向穿透裂纹弯头在平面内弯矩作用下的塑性极限载荷。而纵向表面裂纹对弯头塑性极限弯矩的影响目前还很少有报导。本文通过试验测试了8个无缺陷或有纵向表面裂纹的弯头在内压或平面内弯矩（张开模式）的作用下的载荷—位移曲线，确定了含有纵向表面裂纹弯头的试验塑性极限载荷。

1　弯头试件设计及加工

试验中采用无缝弯头的材料是20#钢，名义外径D0=89 mm，名义壁厚t=5 mm，弯曲半径R0= 120 mm。从弯头上沿纵向切下弧段后压平，按GB6397-86《金属拉伸试验试样》加工成矩形比例试样，然后按GB228-87《金属拉伸试验方法》将试样放在Instron 8032液压伺服材料试验机上进行拉伸，由记录仪自动记录载荷—应变曲线，由于该材料没有明显的屈服平台，所以采用条件屈服强度σ0.2作为材料的屈服强度，并取材料屈服强度σ0.2和抗拉强度σu的平均值作为材料流变应力σf。测得的弯头流变应力为426.39 MPa，延伸率为21.85%。表1中给出的是弯头的实测尺寸。试件包括含有表面裂纹弯头和无缺陷弯头。等效后的裂纹长度及载荷类型如表1所示。其中表面裂纹是用薄铣刀在卧式铣床上加工成的，如图1所示。

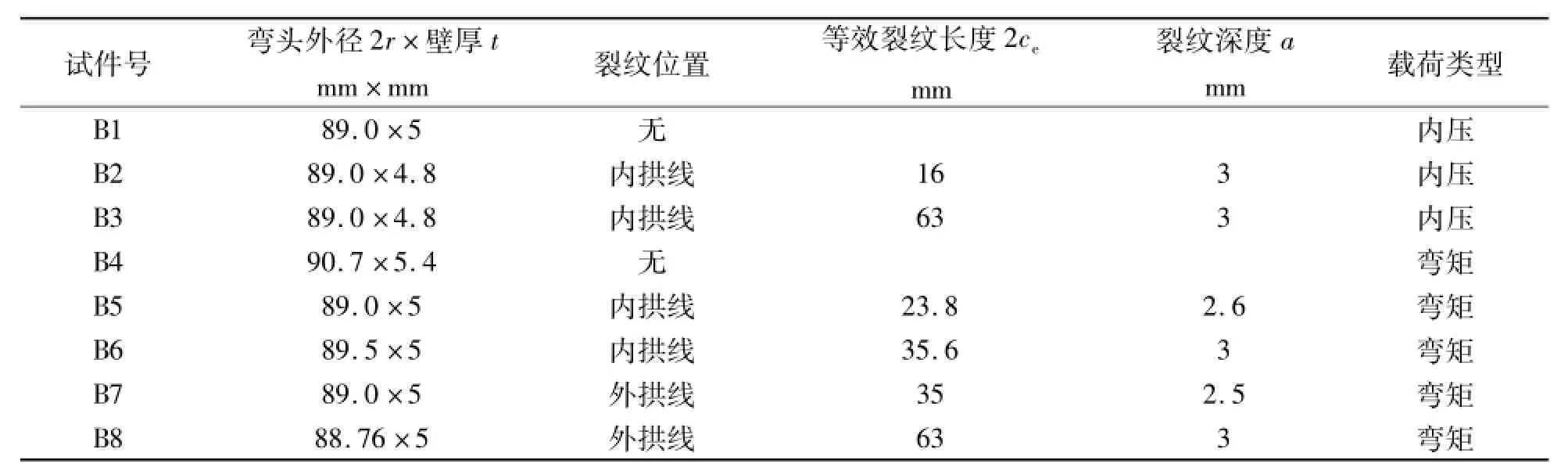
表1　弯头试件缺陷尺寸及载荷类型

图1　含纵向裂纹的弯头

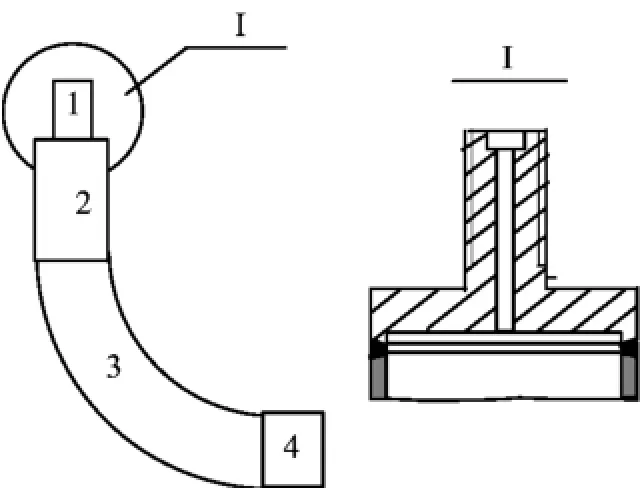
图2　内压作用下弯头测试组件

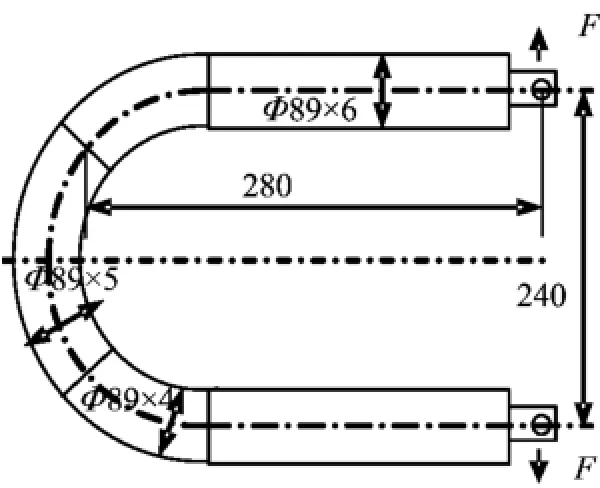
图3　平面内弯矩（张开模式）

为了测内压作用下弯头的塑性极限载荷，同时考虑可多次使用又可避免边缘效应对弯头试件的影响，设计了承受内压载荷的弯头测试组件，如图2所示。图3为用于弯头试件B4-B8的加载组件图，由于与弯头相连的直管长度大于3倍的管径，所以可近似认为弯头受到张开模式的平面内纯弯矩作用，测出的是含裂纹弯头的塑性极限弯矩。

2　试验方法

2.1内压试验

在测定塑性极限压力时，油泵产生的压力由安装在油路中的压力传感器测量，变化V由液位传感器测得，得到压力—体积变化（p-ΔV）曲线。当弯头试件上含表面裂纹时，在裂纹两边安装夹式引伸计，由函数记录仪自动记录，得到压力—裂纹嘴张开位移。然后按JB4732-2005［8］的二倍弹性斜率法，根据压力—体积变化曲线和压力—裂纹嘴张开位移曲线确定无缺陷和有缺陷弯头的极限压力。

2.2平面内弯矩试验

张开模式平面内弯矩作用下弯头的测试在Instron液压伺服试验机上完成，由试验机的记录装置自动记录载荷—加载点位移（F-Δ）曲线或载荷-裂纹嘴张开位移（F-CMOD）曲线，同时在试验过程中用游标卡尺测量一定载荷下弯头中截面（45°处）的直径变化，得到其载荷—椭圆度（F-α）曲线。椭圆度α由式（1）表示：

式中，Dn为弯头的名义直径，D1、D2分别为最小直径和最大直径，分别为弯头中截面几何中性线之间的直径和内外拱线之间的直径。

由二倍弹性斜率法从载荷—加载点位移（FΔ）曲线或载荷—裂纹嘴张开位移（F-CMOD）曲线中即可确定试验塑性极限载荷，试验塑性极限弯矩等于塑性极限载荷与加载点到弯头的水平距离的乘积。

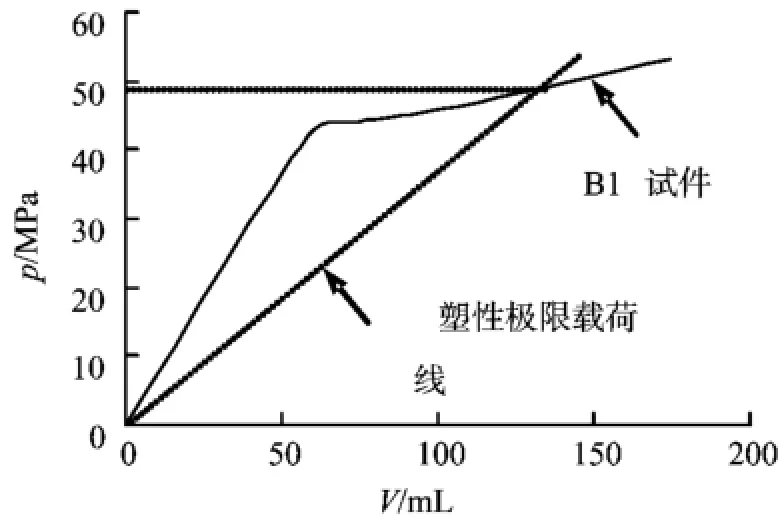
图4　B1试件压力一体积变化曲线

图5　弯头内压爆破图

3　试验结果与分析

3.1内压作用下的弯头极限载荷

图4为无缺陷弯头试件B1在内压载荷作用下的压力—体积变化（p-ΔV）曲线，当压力比较低时，压力与体积变化呈线弹性关系，随着压力的升高，弯头进入塑性强化阶段，没有明显的屈服阶段，与弯头拉伸试样所表现出的性能基本相同。当压力达到爆破压力，在弯头内拱线处发生纵向方向的破裂，如图5所示。这是由于弯头内拱线处的周向应力最大，所以在常温内压爆破试验时，在弯头内拱线处发生纵向破裂而失效，这与文献［9］的试验结果是一致的。根据测得的p-ΔV曲线，实验确定的试验塑性极限压力与按Mises理论得到的分析值比较见表2，显然实测值接近于与理论分析值，两者的相对误差为6.7%［10］。

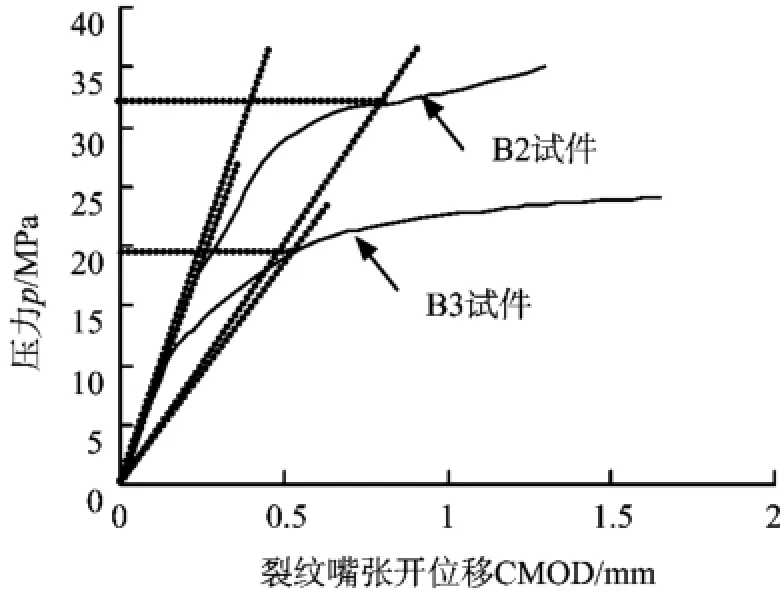
图6　试件B2、B2的p-CMOD曲线

弯头试件B2、B3在内拱线处含不同长度的表面裂纹（裂纹深度相同），在内压载荷作用下，变形主要集中在裂纹韧带处。从图6所示的压力—裂纹嘴张开位移（p-CMOD）曲线可以看出，当压力比较小时，裂纹张开嘴张开位移随着压力增加而线性增加，随着压力的进一步增大，裂纹张开嘴位移与压力不再呈线性关系，而是进入非线性塑性变形阶段，裂纹前沿韧带发生塑性变形。随着压力的继续增大，发生裂纹前沿韧带的撕裂穿透，显然弯头的破裂压力要稍高于塑性极限压力。这也说明在工程中使用限制外载荷不高于塑性极限载荷的方法是保守的，但这样可以保证含缺陷管道安全仍能安全使用。B2和 B3试件对应的试验塑性极限压力与文献［10］分析值比较见表2中。从比较结果看，试验塑性极限压力与理论分析值接近。

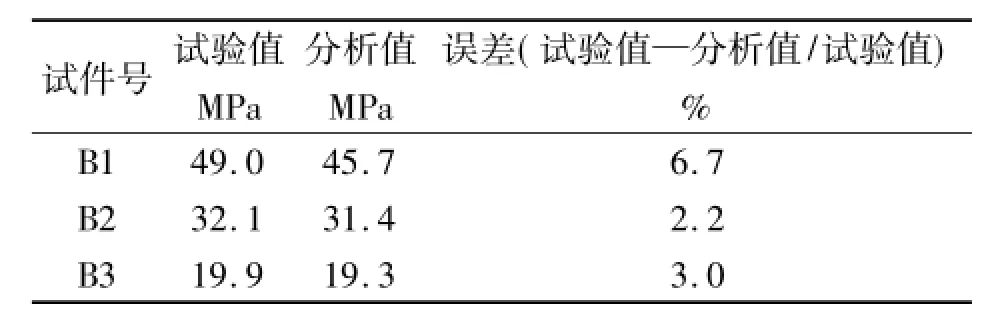
表2　弯头试验极限压力与理论分析比较

3.2平面内弯矩作用下弯头塑性极限弯矩

3.2.1无缺陷弯头

在受到张开模式的平面内弯矩作用时，图7为无缺陷弯头B4试件的载荷—加载点位移（F-Δ）曲线。加载过程中弯头的横截面由圆形变为椭圆形，90°弯头的中截面变形最大，其变形示意图和载荷F-椭圆度α曲线由图8给出，从图8中可以看出：弯头的F-Δ曲线和F-α曲线呈现出相同的规律，即当载荷不大时，加载点位移Δ和椭圆度α与外载荷F保持线性关系，随着外载的继续增大而变成非线性关系。由于外载荷产生一个背离中性轴的力分量，使横截面变形后的抗弯惯性矩增大，从而弯曲阻力增大，所以在弯头塑性阶段加载点位移和椭圆度一直随着外载的增大而增大。但当外载达到塑性极限载荷26.16 kN（弯矩7.33 kN·m）时，弯头的椭圆度并不大，试验测定值为7.8%。

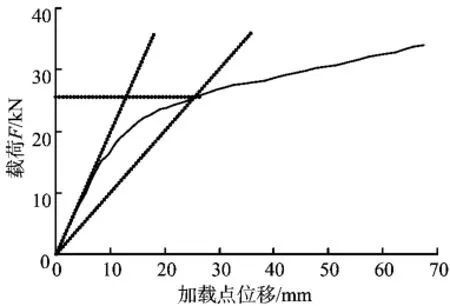
图7　B4试件的F-Δ曲线

图8　B4试件的F-α曲线

无缺陷弯管的理论极限弯矩可用Kitching［12］提出的方法计算，从图9中可以看出B4实测结果要稍大于理论值，这是因为Kitching方法是基于小变形，未考虑弯头椭圆度的影响。但由于在达到塑性极限载荷时弯头的椭圆度不大，所以考虑或忽略椭圆度影响所带来的误差也不大。

图9　塑性极限弯矩实验值与分析值比较

3.2.2含纵向表面裂纹弯头

为了真实地反映含表面裂纹弯头的塑性极限载荷，在试验过程中记录了弯头试件B5至B8，在受到张开模式平面内弯矩作用时的载荷—裂纹嘴张开位移（F-CMOD）曲线，试验塑性极限弯矩见图9。为了便于对比分析，图10、11给出了试件B5和B7的裂纹中心附近弯头的横截面载荷F-椭圆度曲线及F-CMOD曲线。

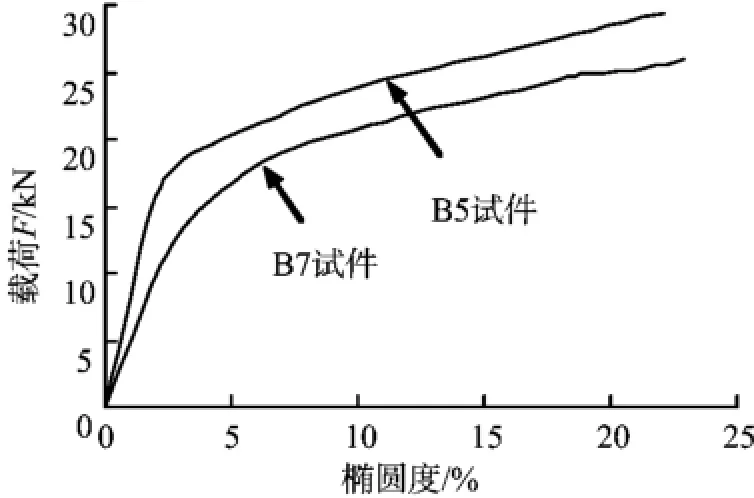
图10　B4试件的F-Δ曲线

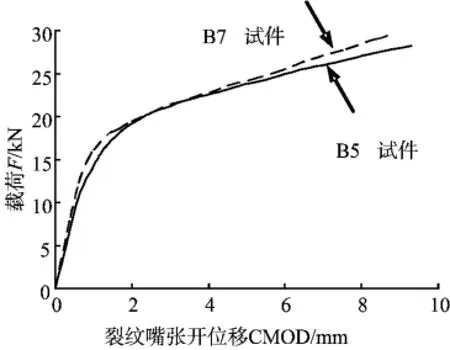
图11　B4试件的F-α曲线

从图中可以看出在张开模式的平面内弯矩作用下，内拱线和外拱线处含表面裂纹的弯头横截面变形规律与相同受载条件下无缺陷弯头相同，即几何中性线之间的直径变小，内外拱线之间的直径变大。从测试结果看，含表面裂纹的弯头试件达到塑性极限载荷时椭圆度不大，为6%～7%。从图中可见试验塑性极限弯矩与理论值接近，但由于理论值没有考虑弯头变形时的弯曲阻力增大，所以实测值比理论值稍偏大也是合理的［10］。

4　结论

通过对8个无缺陷或有缺陷Φ89 mm×5 mm的弯头试样的内压或平面内弯矩试验，根据测试曲线和相关规范确定了每个弯头试件的塑性极限载荷，主要结论有：①含缺陷弯头的试验塑性极限载荷比无缺陷弯头的小，说明裂纹的存在会降低弯头的承载能力，承载能力的降低程度与裂纹的长度、深度及位置有关；②内压作用下无缺陷弯头的失效位置是在内拱线处纵向方向，并且试验塑性极限压力和理论值很接近，理论略偏保守。③张开模式的平面内弯矩作用下的无缺陷弯头和含缺陷弯头的试验塑性极限弯矩比基于小变形分析得到的理论值偏大（误差≤15%），通过试验说明了在工程上应用小变形分析进行塑性极限弯矩预测也是可行的。

参考文献：

［1］Calladine C R.Limit analysis of curved tubes［J］.Journal of Mechanical Engineering Science，1974，16（2）：85-87.

［2］Kitching，Zarrabi&Moore.Limit moment for smooth pipe bend under in-plane bending［J］.Int J Mech Sci，1979，21：731-738.

［3］段志祥.平面闭合弯矩作用下弯管塑性极限载荷分析与试验［J］.石油化工设备，2005，34（2）：8-10.

［4］Chattopadhyay J，Nathani D K，Dutta B K，et al.Closedform collapse moment equations of elbows under combined internal pressure and in-plane bending moment［J］. Journal of Pressure Vessel Technology，Transactions of the ASME，2002，122：431-436.

［5］王辰，李培宁.内压载荷作用下含缺陷弯头的塑性极限载荷有限元分析［J］.压力容器，2005，22（8）：6-9.

［6］Kastner W.Critical crack sizes in ductile piping［J］.International Journal of Pressure Vessels and Piping，1981 （9）：197-219.

［7］Griffiths J E.The effect of cracks on the limit load of pipe bends under in-plane bending：experimental study［J］. Int J Mech Sci，1979，21：119-130.

［8］JB4732-2005，钢制压力容器——分析设计标准［S］.北京：中国标准出版社，2005.

［9］王行山.弯管断裂原因的研究现状和存在问题评述［J］.电力建设，1984（3）：21-25.

［10］ 郭茶秀.内压及扭矩载荷下无缺陷弯管的塑性极限载荷［J］.机械强度，2003，25（3）：315-318

中图分类号：TQ050.3

文献标识码：A

文章编号：1003-3467（2016）04-0026-05

收稿日期：2016-02-17

基金项目：国家自然科学基金（51176173）和河南省科技攻关计划项目（162102210001）

作者简介：马凤兰（1964-），女，工程师，从事安全方面的研究与教学工作；联系人：郭茶秀（1968-），女，教授，研究方向为新能源利用与设备安全，E-mail：guochaxiu@163.com。

Experimental Research on Limit Load of Elbow Containing Crack

MA Fenglan1，GUO Chaxiu2*
（1.Zhengzhou Safety Production Education Center，Zhengzhou450006，China；2.School of Chemical Engineering and Energy，Engineering Research Center of energy saving technology and equipment of thermal energy system，Zhengzhou university，Zhengzhou450001，China）

Abstract：In order to study the ultimate bearing capacity of the elbow containing defects，the in-plane bending moment test of the internal pressure and the open mode of eight seamless elbow specimens is designed and carried out，the corresponding pressure volume change curve，pressure crack mouth opening displacement curve，force loading point displacement curve or force crack mouth opening displacement curve are recorded for the defect free and defective elbows，and the relationship between the ellipse degree and the bending moment load of the elbow section is analysised.According to the curve obtained from the test，the plastic limit load of the eight bend specimens is determined，and the experimental results are compared with the relevant theories.

Key words：elbows；limit load；crack