三维J积分理论在固体火箭发动机裂纹研究中的应用

徐学文，任建存，倪保航

（海军航空工程学院a.接改装训练大队；b.控制工程系，山东烟台264001）

三维J积分理论在固体火箭发动机裂纹研究中的应用

徐学文a，任建存b，倪保航a

（海军航空工程学院a.接改装训练大队；b.控制工程系，山东烟台264001）

针对固体火箭发动机药柱上裂纹的三维性和受力复杂性，文章提出采用三维J积分理论和数值仿真来计算药柱上裂纹缝线上的J积分值，并给出了三维J积分的体积分表达式和有限元数值分析方法；通过对固体火箭发动机药柱上在燃烧室星角处的一条典型裂纹——横向贯穿楔形裂纹仿真计算，得出裂纹缝线上J积分值呈现中间高两端低的非均匀分布特点，证明了三维J积分理论在固体火箭发动机装药裂纹危险性研究上的适用性。

固体火箭发动机；裂纹；三维J积分；数值仿真

自上个世纪以来，人们开始将固体材料断裂学理论[1]引入到固体火箭发动机药柱裂纹扩展机理的研究中来[2-4]。随着研究的深入，逐步发现，K判据和G判据仅适用于裂纹尖端屈服区很小的或脆性断裂的材料，不适合固体火箭发动机推进剂等屈服强度比较大的粘弹性材料[5-6]；COD断裂准则虽然采用裂纹尖端张开位移能够描述弹塑性材料裂纹的危险程度，但它只是采用经验公式来表征材料断裂韧性[7-8]。而Rice提出的J积分概念[9]，巧妙地避开了求解裂纹尖端前缘屈服区的应力场和应变场所遇到的数学困难，并且经过数学上的严格证明，平面型裂纹J积分计算与路径无关。因此，J积分更适合固体装药为粘弹性材料[10]的固体火箭发动机药柱裂纹危险性研究。由于固体火箭发动机药柱上裂纹的三维性和受力复杂性，裂纹缝线上J积分值分布呈现非均匀性[11]，因而本文提出采用三维J积分理论和数值方法来计算固体火箭发动机药柱裂纹的J积分值，从而为研究裂纹扩展机理和危险性分析提供可靠的理论依据。

1 三维J积分理论

假设药柱裂纹缝线是一条切向连续的线，在其上任意一点s处建立局部坐标系，如图1所示，坐标轴x1在裂纹缝线平面内垂直于裂纹缝线，坐标轴x3与裂纹缝线相切，坐标轴x2垂直裂纹缝线平面。裂纹局部扩展方向用q表示，它垂直于裂纹缝线而位于裂纹平面（x1-x3）内，这样在总体坐标任意点s处垂直于裂纹缝线的平面（x1-x2）内，可写出不依赖于路径的任意积分回路Γ上的J积分：

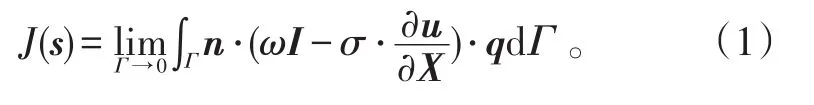
式（1）中：n是积分路径Γ的法向；ω是应变能，对粘弹性材料，它包括弹性应变能和塑性耗散能；u是积分回路的位移矢量。

将平面上定义的二维J积分沿着裂纹缝线逐点积分可得裂纹缝线的三维J积分为：

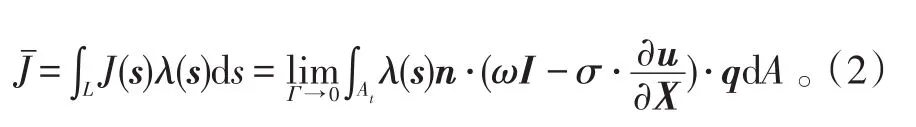
式（2）中：L表示裂纹缝线长度；d A是包绕裂纹缝线的圆柱曲面上的面积微元，d A=d s dΓ；n表示微元d A的外法线方向；λ(s)是裂纹缝线s点处的长度。

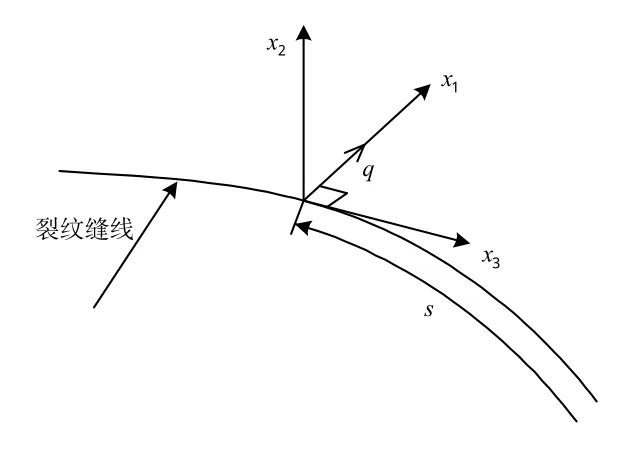
图1 局部坐标Fig.1 Localorthogonal cartesian coordinates

为了计算Jˉ，需要将式子中的面积分转换为体积分，围绕着裂纹缝线建立一个封闭轮廓的积分曲面，如图2所示。Ao是沿着裂纹缝线方向的外层圆柱曲面，At是内层圆柱曲面，Aends是裂纹缝线两端的端面，Acracks是裂纹腔上下两裂纹面。 Ao、At、Aends和 Acracks组成的曲面A形成了一个体积为V的体积分区域。在体积分区域内定义一个权函数qˉ，在At上qˉ的模为0，在Ao上qˉ=λ(s)q，在曲面A内qˉ在这2个值之间平滑变化，在Aends面上，沿裂纹扩展方向的单位矢量q不一定与 Aends相切，但必须确切地给出 Aends面的法向。因此式（2）可以写成曲面A上的面积分为：

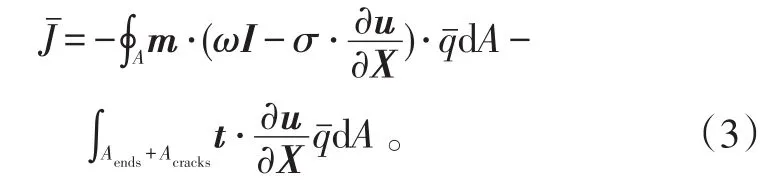
式（3）中：m是封闭曲面A上的法向矢量，在Ao上m=-n；t=m⋅σ是端面Aends和裂纹面Acracks上的表面张力。

根据高斯定理把封闭曲面上的面积分转化为体积分得三维J积分为：

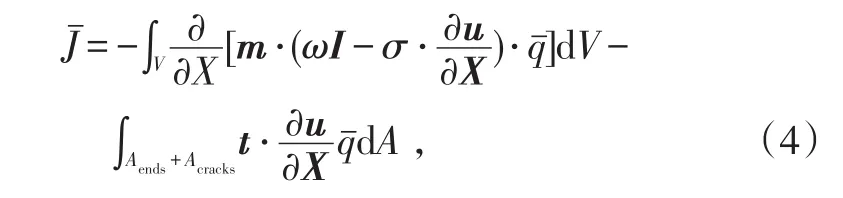
式中，V是封闭曲面所围成的体积。

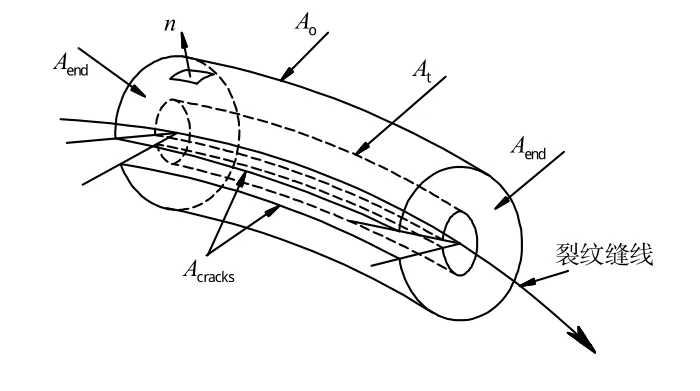
图2 积分曲面Fig.2 Integralsurface

2 J积分数值计算方法

本文以五角星型内孔燃烧固体火箭发动机药柱上，在燃烧室星角处存在的一条典型裂纹——横向贯穿楔形裂纹为计算对象，见图3，说明J积分数值计算方法[12-13]，计算模型内的裂纹缝线是裂纹腔2个侧平面的交线，是一条直线段。采用非线性有限元法[14]计算发动机药柱的应力应变和裂纹缝线上各节点处的J积分值。

在有限元模型中，沿着裂纹缝线某节点p处的λ(s)可以写成有限元单元的形函数形式，即

式（5）中：Np(s)为形函数，在节点p处，λp=1；在其他节点上λp=0。本文所采用的离散单元为8节点六面体单元和4节点四面体单元[15]。

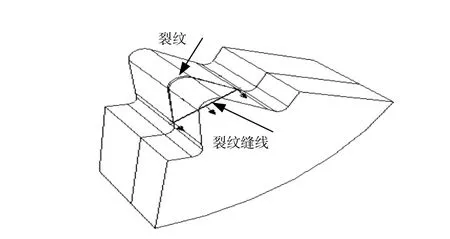
图3 药柱上的裂纹、裂纹缝线和虚拟裂纹扩展方向Fig.3 Crack in grain，crack front line and the virtual crack extension direction

这样，在裂纹缝线上每一节点p的J积分值可以表示为

在计算过程中[16-17]，首先指定裂纹的缝线。然后，指定积分的轮廓数N。积分轮廓是包绕在裂纹尖端或裂纹缝线上的从一个裂纹面上开始到对面裂纹面结束的一串单元，这N个轮廓单元围绕着裂纹缝线从里到外层层包绕，这些积分轮廓上的积分将被转换为包绕区域的面积分（二维）和体积分（三维）。本文设定的积分轮廓数为5，以便鉴别各轮廓上算出的J积分值的有效性。

最后，还要指定裂纹缝线上各点的虚拟裂纹扩展方向，一般通过指定裂纹缝线所在平面的法向或者直接指定扩展方向来完成。由于本文要计算的裂纹缝线为直线，所以这里直接指定裂纹虚拟扩展方向，整个裂纹缝线的扩展方向在裂纹体沿轴向的中心对称平面内垂直裂纹缝线向内，如图3中箭头所示。

3 仿真结果

深度为43mm的裂纹在燃气压力（裂纹腔进口平均压力[18]为0.385MPa）作用下，药柱横截面上M ises应力分布如图4所示，在裂纹缝线附近产生应力集中，在裂纹缝线上，中间部位应力最高，然后沿着裂纹缝线由中间向两端应力逐渐递减，呈现出均匀性。

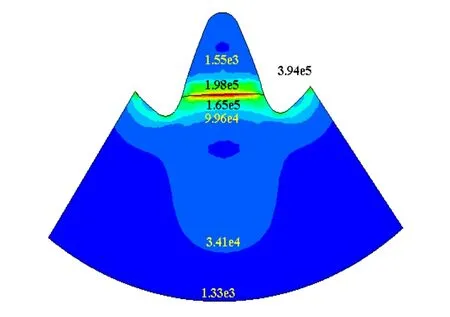
图4 在包含裂纹缝线的药柱横截面上Mises应力分布Fig.4 M isesstressdistribution on thehorizontalsection ofgrainw ith the crack front

裂纹缝线上J积分值分布见图5，J积分值呈现出中间高两端低的分布趋势，缝线中间部位的J积分值最大，此处裂纹点最易先扩展。这是因为药柱星角体横截面是顶部窄底部宽的形状，裂纹缝线上各点的裂纹深度不一样，在固体火箭发动机工作过程中，裂纹腔壁面上中央靠近裂纹缝线部位作用的燃气压力比较高，此处的推进剂变形比较大，造成该型裂纹缝线上J积分值呈现中间高两端低的非均匀分布趋势。

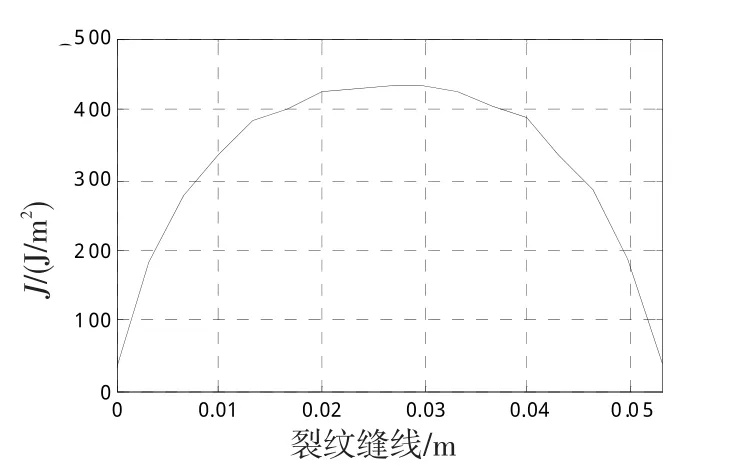
图5 沿裂纹缝线上的J积分分布Fig.5　J-integraldistribution along the crack front line

改变裂纹腔进口压力，计算出不同压力下裂纹缝线上的J积分值，如表1所示。从表1看出，不同压力下的裂纹缝线上J积分值沿着缝线的分布类似于图5所示的分布曲线——中间高两端低。在压力低的情况下，这种分布曲线趋向平缓；压力越高，曲线中间部位越凸起，裂纹缝线中间部位的点更容易扩展。

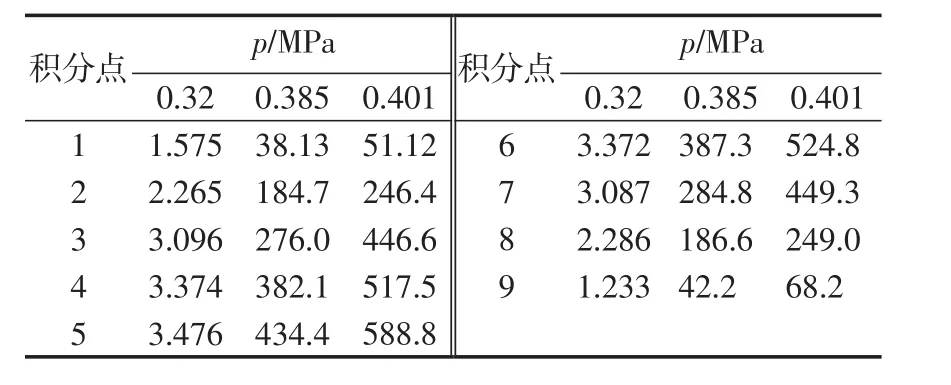
表1 43 mm深的裂纹在不同压力下缝线上的J积分值Tab.1 J-integralvalueson the crack front line of crack cavity w ith 43mm depth under differentpressures

4 结论

固体火箭发动机药柱为粘弹性材料，药柱上裂纹扩展机理研究宜采用适合大范围屈服的，并经过数学严格证明与积分路径无关的J积分理论；通过高斯定理变换，将二维J积分计算公式扩展到三维J积分计算公式，再采用有限元计算方法，得到了发动机药柱上燃烧室星角处横向贯穿裂纹缝线上J积分值呈现中间高两端低的分布特点，证明了三维J积分理论在固体火箭发动机装药裂纹等缺陷扩展机理研究上的适用性。

[1]王自强，陈少华.高等断裂力学[M].北京:科学出版社，2009：3-9.

WANG ZIQIANG，CHEN SHAOHUA.Advanced fracturemechanics[M].Beijing：Science Press，2009：3-9.（in Chinese）

[2]PROSENJITD，SINGH IV，JAYAGANTHAN R.An experimental evaluation ofmaterial properties and fracture simulation of cry rolled 7075Alalloy[J].Journalof Materials Engineering and Performance，2012，21（7）：1167-1181.

[3]BOUVARD JL，CHABOCHE JL，FEYEL F.A cohesive zonemodel for fatigue and creep：fatigue crack grow th in single crystal super alloys[J].International Journal of Fatigue，2009，31（5）：868-879．

[4]MARIANIS，PEREGO U.Extended finite elementmethod for quasi-brittle fracture[J].International Journal for Numerical Methods in Engineering，2003，58（2）：103-126．

[5]MOES N，BELYTSCHKO T.Extended finite element method for cohesive crack grow th[J].Engineering FractureMechanics，2002，69（7）：813-833.

[6]杨志锋，周昌玉，代巧.基于扩展有限元法的弹塑性裂纹扩展研究[J].南京工业大学学报，2014，36（4）：50-57.

YANG ZHIFENG，ZHOU CHANGYU，DAIQIAO.Elastic-plastic crack propagation based on extended finite elementmethod[J].Journalof Nanjing Technology University，2014，36（4）：50-57.（in Chinese）

[7]ROE K L，SIEGMUND T.An irreversible cohesive zone model for interface fatigue crack grow th simulation[J]. Engineering FractureMechanics，2003，70（2）：209-232．

[8]LIU PF，ZHANG B J，ZHENG JY.Finite elementanalysisof plastic collapse and crack behavior of steel pressure vessels and piping using XFEM[J].Journal of Failure Analysisand Prevention，2012，（12）：707-718．

[9]YANG DAPENG，CHEN XI，ZHAOYAO，etal.The J-integral of a slightly curved elasticity-plasticity crack when enduring quasi static loads[J].International Journal of PlantEngineering and Management，2014，19（1）：6-11.

[10]徐学文，彭军，单鑫.固体火箭发动机HTPB推进剂力学性能老化研究[J].海军航空工程学院学报，2014，29 （1）：53-56.

XU XUEWEN，PENG JUN，SHAN XIN.Ageing investi-gation onmechanics propertiesof HTPB propellant in the solid rocketmotor[J].Journal of naval Aeronautical and Astronautical University，2014，29（1）：53-56.（in Chinese）

[11]徐学文，辛庆伟，牟俊林.固体火箭发动机药柱裂纹扩展判据的统计分析[J].固体火箭技术，2015，38（5）：657-659.

XU XUEWEN，XIN QINGWEI，MU JUNLIN.Statistic analysis of the propagation criterion about grain crack in solid rocketmotor[J].Journal of Solid Rocket Technology，2015，38（5）：657-659.（in Chinese）

[12]GOLEWSKIG L，GOLEWSKIP，SADOWSKIT.Numericalmodeling crack propagation under ModeⅡfracture in plain concretes containing siliceous fly-ash additive using XFEM method[J].Computational Materials Science，2012，62（1）：75-78．

[13]邢文金.基于有限元的弹塑性裂纹数值分析[J].科技创新导报，2013（15）：91-93.

XINGWENjIN.Numerical analysis of elastoplastic crack based on the finite element[J].Science and Technology Innovation Herald，2013（15）：91-93.（in Chinese）

[14]张玉峰，朱以文，丁宇明.有限元分析系统ABAQUS中的特征技术[J].工程图学报，2006，27（5）：142-148.

ZHANG YUFENG，ZHU YIWEN，DING YUM ING.The ABAQUS technology of finite element analysis system [J].Journal of Engineering Graphics，2006，27（5）：142-148.（in Chinese）

[15]LABORDEP，POMM IER J，R ENARD Y，etal.High-order extended finite elementmethod for cracked domains [J].International Journal for Numerical Methods in Engineering，2005，64：354-381.

[16]CHAHINE E，LABORDE P，R ENARD Y.A quasi-optimal convergence result for fracture mechanics w ith XFEM[J].Computes Rendus Mathematigue，2006，342：527-532.

[17]庄卓，张帆，岑松.ABAQUS非线性有限元实例[M].北京：科学出版社，2006：120-127.

ZHUANG ZHUO，ZHANG FAN，CEN SONG.ABAQUS nonlinear finite element analysis and examples[M]. Beijing：Science Press，2006：120-127.（in Chinese）

[18]徐学文，邓会光，牟俊林.HTPB复合推进剂燃速对固体火箭发动机内弹道性能影响[J].海军航空工程学院学报，2014，29（6）：506-510.

XU XUEWEN，DENG HUIGUANG，MOU JUNLIN.Effects of HTPB composite propellant burning rate on the solid-rocket-motor internal ballistic characteristics[J]. Journalof NavalAeronauticaland AstronauticalUniversity，2014，29（6）：506-510.（in Chinese）

Application of 3-D J-integral Theory in the Solid RocketMotor Crack Reasearch

XUXuewena,REN Jiancunb,NIBaohanga

（Naval Aeronauticaland AstronauticalUniversity a.Training brigade ofEquipmentAcceptance and Modification; b.DepartmentofControlEngineering,YantaiShandong 264001,China）

Aiming to the 3-D characteristics of the crack and its force application complexity in solid rocketmotor grain, the application of3-D J-integral theory and numericalsimulation to calulate the J-integralvalues at the Gauss integration pointsof the crack linewasproposed in the dissertation,and the 3-D volumic J-integralexpression and the finite-element numerical analysismethod were given out.Thewedge crack which traversed through the projection of star grain was simu⁃lated as a typical crack in solid rocketmotor.As shown in the calculation results,the J-integral distribution along the crack front line behaved as the varying characteristicsofhigh valueat the centerand low value in both sides,which proved that3-D J-integralcalculationmethod was suitable to reasearch the risk ofsolid rocketmotorgrain crack.

solid rocketmotor;crack;3-D J-integral;numericalsimulation

V435

A

1673-1522（2016）02-0117-04

10.7682/j.issn.1673-1522.2016.02.004

2015-11-18；

2016-01-19

徐学文（1971-），男，副教授，博士。