一类非局部薛定谔方程的解的存在性*1

厉少军， 杨敏波

（浙江师范大学数理与信息工程学院，浙江金华　321004）

一类非局部薛定谔方程的解的存在性*1

厉少军， 杨敏波

（浙江师范大学数理与信息工程学院，浙江金华321004）

研究了一类扰动的Choquard型方程非平凡解的存在性，通过采用Lyapunov-Schmidt约化方法及Ambrosetti-Badiale理论，证明了该方程的非平凡弱解的存在性定理.

非局部薛定谔方程；变分方法；临界点；古典解

0　引言

近年来，许多学者研究了Gross-Pitaevskii方程

稳态解的存在性.式（1）中：参数m是玻色子的质量；ħ是普朗克常量；i为虚数单位；W（x）是位势函数.文献［1］利用临界点定理研究了Choquard-Pekar方程

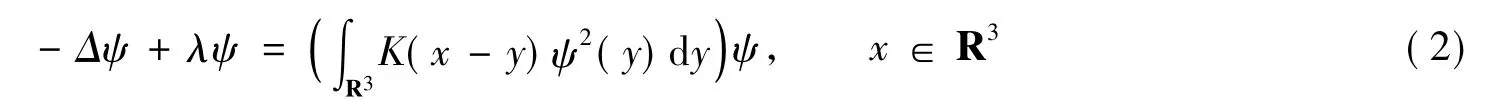
在空间H1（R3）中非平凡解的存在性.式（2）中，K（x）是给定的引力位势.文献［2］在径向对称函数空间中利用变分方法证明了非线性Choquard型方程

非平凡解的存在性，且当R（x）和K（x）满足一定条件时，该解为古典解.文献［3］证明了当3≤p＜5时Schrödinger-Maxwell系统（也就是Schrödinger-Poisson方程）

的径向对称孤立波的存在性和山路型解的存在性.文献［4-6］也研究了Schrödinger-Poisson方程解的存在性；文献［7-8］对于有限维空间通过Lyapunov-Schmidt约化方法建立了研究这一类方程的一些理论.这种方法也被用于其他的一些变分问题［9-11］.

本文采用扰动方法考虑一类Choquard型方程解的存在性，即考虑扰动方程

解的存在性.式（5）中，0＜τ＜min｛4，N｝.

1　一　些命题及引理

命题1［12］（Hardy-Littlewood-Sobolev不等式）若p＞1，r＞1，0＜μ＜N，，f（x）∈Lp（RN）且h（y）∈Lr（RN），则存在独立于f（x），h（y）的常数C（p，μ，N，r），使得

命题2［13］若对于，则

存在唯一的正的径向解U，且满足以下衰减性质：

其中：C是一正常数；I0：H1（RN）→R为

U是C2泛函I0的临界点.记I0的临界点集组成的一个N维流形为

设

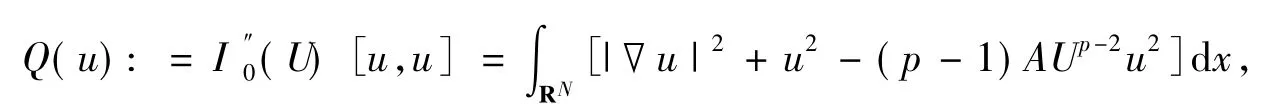
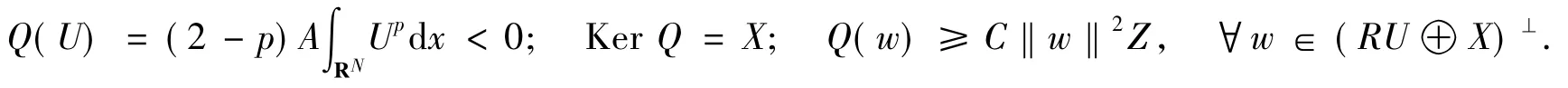
下面运用命题1和命题2研究扰动泛函临界点的存在性问题.设E是一个实的Hilbert空间，其上的一个扰动泛函表示为

式（7）中：I0：E→R；G：R×E→R.I0（u）和G（ε，u）需满足以下关系：

1）I0∈C2，G∈C2；

2）G是连续函数，且对于任意的u，有G（0，u）=0；

3）G'（ε，u）和G″（ε，u）分别是R×E→E和L（E，E）上的连续映射，其中：L（E，E）是E→E的线性连续算子；

4）Z是一个d维的C2流形且由I0的临界点组成，这样的Z也称为I0的临界流形；

5）设TθZ是Z定义在zθ处的正切空间，流形Z是非退化的，Ker（I″0（z））=TθZ，其中：对于任意的zθ∈Z，（zθ）是一个指标为0的Fredholm算子；

对于扰动问题临界点的存在性研究，就是考虑I'ε（u）=0解的存在性.现需要寻找形如u=z+w的解，其中，z∈Z，w∈W=（TθZ）⊥.运用Lyapunov-Schmidt约化，可以将原来的问题降低到有限维上，即等同于解决下面的问题：

其中：P是空间E到W的正交投影.对u=z+w（ε，z），运用Taylor展开，可得

引理1［7-8］若I0（u）和G（ε，u）满足条件1）～6），且对∀ε＞0，存在δ＞0和z*∈Z，使得

则Iε存在一个临界点uε.

2　定理1　及其证明

定理1若且

则方程（5）至少存在一个非平凡弱解.式（9）中，U是命题2中的径向解.

下面应用命题1、命题2及引理1来证明定理1.

首先考虑方程（5），其相应的能量泛函Iε：H1（RN）→R可以定义为

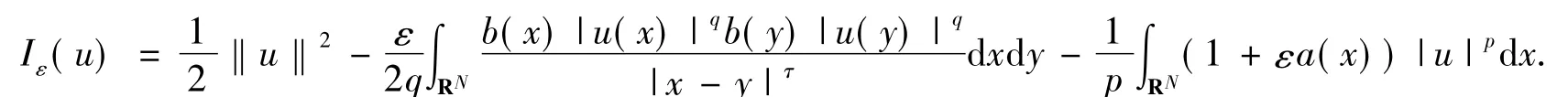
定理1证明若

则能量泛函Iε（u）可以被表示为

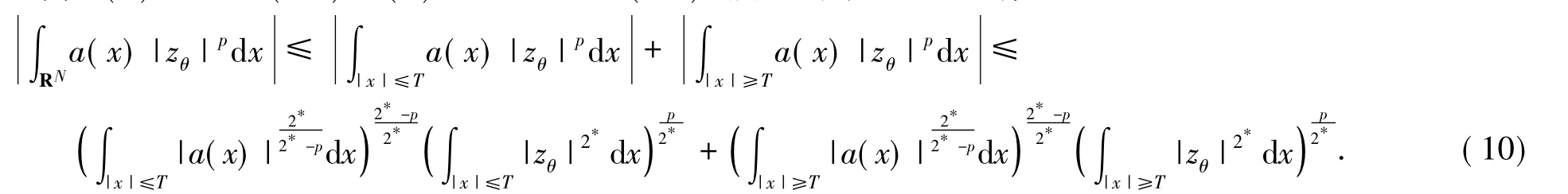
另一方面，由于U在无穷远处按指数衰减，从而存在Mε，使得对于θ＞Mε，有

由式（11）和式（12）可得，

同样地，由命题1可知，

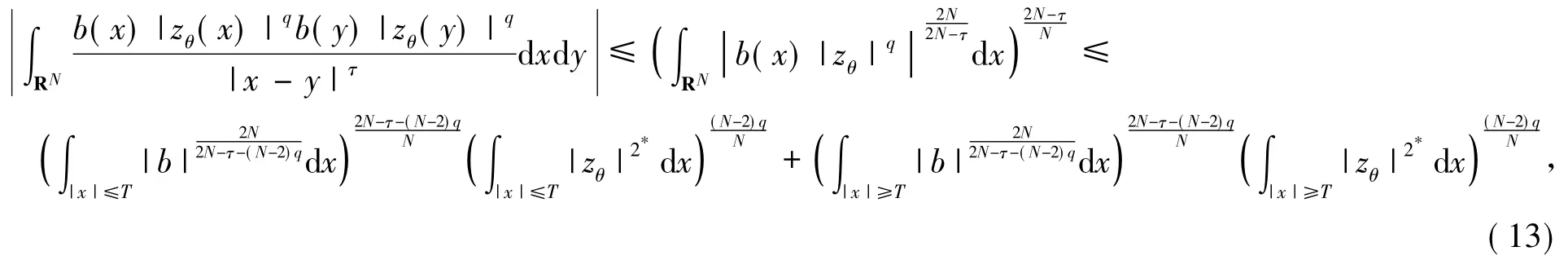
从而

即

又由

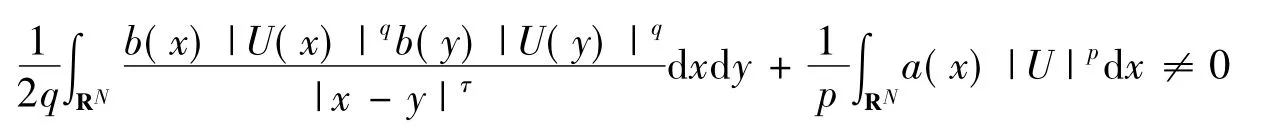
可知Γ（0）≠0，从而由引理1可知定理1成立.定理1证毕.

［1］Lions P L.The Choquard equation and related questions［J］.Nonlinear Anal，1980，4（6）：1063-1072.

［2］Menzala G.On regular solutions of a nonlinear equation of Choquard＇s type［J］.Proc Roy Soc Edinb，1980，86（3）：291-301.

［3］d＇Aprile T，Mugnai D.Solitary waves for nonlinear Klein-Gordon-Maxwell and Schrödinger-Maxwell equations［J］.Proc Roy Soc Edinb，2004，134（5）：1-14.

［4］Ambrosetti A.On Schrödinger-Poisson systems［J］.Milan JMath，2008，76（1）：257-274.

［5］d＇Avenia P，Mederski J.Positive ground states for a system of Schrödinger equations with critically growing nonlinearities［J］.Calc Var Partial Differential Equations，2015，53（3）：879-900.

［6］Azzollini A，d＇Avenia P，Luisi V.Generalized Schrödinger-Poisson type systems［J］.Commun Pure Appl Anal，2013，12（2）：867-879.

［7］Ambrosetti A，Badiale M.Homoclinics：Poincaré-Melnikov type results via a variational approach［J］.Ann Inst H Poincare Anal Non Lineaire，1998，15（2）：233-252.

［8］Ambrosetti A，Badiale M.Variational perturbative methods and bifurcation of bound states from the essential spectrum［J］.Proc Royal Soc Edinb，1998，128（6）：1131-1161.

［9］Ambrosetti A.Semiclassical states of nonlinear Schrödinger equations［J］.Arch Rat Mech Anal，1997，140（3）：285-300.

［10］Badiale M，Pomponio A.Bifurcation results for semilinear elliptic problems in RN［J］.Proc Roy Soc Edinb，2004，134（1）：11-32.

［11］Ianni I，Vaira G.Non-radial sign-changing solutions for the Schrödinger-Poisson problem in the semiclassical limit［J］.NoDEA Nonlinear Differential Equations Appl，2015，22（4）：741-776.

［12］Lieb E，Loss M.Analysis［M］.2nd.Providence：American Mathematical Society，2001：1-346.

［13］Ambrosetti A，Malchiodi A.Perturbation methods and semilinear elliptic problems on RN［M］.Basel：Birkhäuser Verlag，2006：1-183.

（责任编辑陶立方）

Existence of nontrivial solutions for a class of nonlocal Schrödinger equations

LIShaojun， YANG Minbo
（College of Mathematics，Physicsand Information Engineering，Zhejiang Normal University，Jinhua 321004，China）

Itwas discussed the existence of nontrivial solutions for some disturbance Choquard type equations. Some existence results for this equation were established by Lyapunov-Schmidt reduction procedure and Ambrosetti-Badiale＇s theories.

nonlocal Schrödinger equation；variationalmethods；critical points；classical solutions

O175.25

A

1001-5051（2016）02-0146-04

10.16218/j.issn.1001-5051.2016.02.004

*收文日期：2015-06-08；2015-11-23

国家自然科学基金资助项目（11271331）

厉少军（1990-），男，安徽滁州人，硕士研究生.研究方向：非线性泛函分析.

杨敏波.E-mail：mbyang@zjnu.cn