有限体积法与正交试验法相结合的动静压轴承结构优化设计

孟曙光　熊万里　王少力　吕　浪　郑良钢

1.湖南大学国家高效磨削工程技术研究中心，长沙，410082 2.湖南海捷主轴科技有限公司，长沙，410082



有限体积法与正交试验法相结合的动静压轴承结构优化设计

孟曙光1熊万里1王少力1吕浪1郑良钢2

1.湖南大学国家高效磨削工程技术研究中心，长沙，410082 2.湖南海捷主轴科技有限公司，长沙，410082

针对小孔节流深浅腔动静压轴承的性能优化问题，基于平行平板扩散流动计算模型及流量守恒原理，推导了微元控制体边界压力的插值函数，提出了分析小孔节流深浅腔动静压轴承的油腔压力、承载力、静刚度、进油流量及温升等承载特性的有限体积计算方法。使用该方法研究了供油压力、主轴转速、进油孔径、浅腔深度、初始油膜厚度等参数对小孔节流深浅腔动静压轴承承载特性的影响规律，从而得到了以上相关参数的优化区间。在此基础上，采用四因素三水平的正交试验法，在满足多目标性能最优的前提下，得到了小孔节流深浅腔动静压轴承结构参数与工作参数的最优组合。以该组参数试制了小孔节流深浅腔动静压轴承并建立了试验平台，测量了不同转速及供油压力下油腔的压力值。试验结果表明，轴承油腔压力试验数据及理论计算值随主轴转速的变化趋势一致；误差在11%以内。验证了有限体积法与正交试验法相结合的动静压轴承结构优化设计方法的正确性。

有限体积法； 正交试验法；小孔节流；深浅腔动静压轴承；承载特性；结构优化

0　引言

深浅腔动静压混合轴承[1-2]具有抗过载能力强、稳定性好、对负载变化敏感性低等优点，因而被广泛地应用于高速精密磨床的静压主轴上。在设计工作中，选取深浅腔动静压轴承结构参数及工作参数的主要依据，是以油腔压力、承载能力、油膜刚度、进油流量及温升为代表的承载特性[3-4]。如果参数选取不当，会造成油膜刚度不足及温升过高，进而导致磨削质量下降，严重时可导致主轴刮擦、抱轴等事故。因此，选取合适的轴承结构参数及工作参数是获得最优承载特性的关键。

已有学者对优化深浅腔动静压轴承的承载特性进行了研究。孙恭寿等[5]采用解析法及有限差分法对环面缝隙节流深浅腔动静压轴承进行了研究，但未能进一步研究动静压轴承的优化设计问题。郭胜安等[6]采用FLUENT软件研究了深浅腔动静压轴承的工作参数和结构参数对轴承刚度、流量及温升的影响规律，并给出了参数的优选区间。Wang等[7]通过求解动态雷诺方程及能量方程得到了轴承平均温升、承载能力、油流率及涡动频率等参数，但仅研究了两个备选方案。上述研究结果表明，寻找动静压轴承优化设计的最优的参数组合，是一个多目标优化问题[8]，它存在计算工作量大、用时长的困难。

本文改变了将正交试验法仅用于试验领域的传统习惯，把它移植到理论计算领域。根据平行平板扩散流动计算模型，依据控制体及其边界上流量守恒的物理本质，得到了微元控制体边界上压力的插值函数，提出了分析小孔节流深浅腔动静压轴承的油腔压力、承载能力、静刚度、进油流量及温升等承载特性的计算方法。进而用该方法研究了动静压轴承的供油压力、主轴转速、进油孔径、浅腔深度、初始油膜厚度等参数对轴承承载特性的影响规律，并确定了参数的优化区间。在此基础上，采用四因素三水平的正交试验法，在满足多目标性能最优的前提下，从理论上研究了该轴承结构参数与工作参数的最优组合。以该组参数试制了试验平台，并测量了不同转速及供油压力下油腔的压力值。

1　有限体积法

1.1轴承结构及工作原理

图1为小孔节流深浅腔动静压轴承的结构图。在轴承的对称中心处建立直角坐标系，水平向右为X轴，竖直向上为Y轴，垂直纸面向外为Z轴。圆周均布的4个油腔从右下起按逆时针依次编号为1、2、3、4。以第1油腔为例，轴承的结构参数如下：周向封油边包角为φb，深腔包角为φc。深腔油腔深度为hs，浅腔油腔深度为hp。

图1　小孔节流深浅腔动静压轴承结构图

在供油压力ps作用下，润滑油经过小孔节流器进入深腔，在逆时针旋转的轴颈的迁移作用及深浅腔之间二次节流作用下流向浅腔，并在浅腔末端形成压力远大于深腔压力的动压。最后润滑油流过周向封油边进入回油槽或从轴向端面回油。静止时，在静压效应作用下，主轴通过作用在有效承载面积的上下油腔压差承载；转动时，主轴主要靠远大于深腔油压的动压力工作。

1.2基本假设

做如下假设：①润滑油流动状态为层流；②在载荷作用下轴心竖直向下偏移(偏位角始终为0)；③基于等温假设；④全部发热量均由润滑油吸收并由端泄带走，发热量与端泄散热平衡，即“绝热流动”。

1.3物理方程

1.3.1平行平板扩散流动方程

一维雷诺方程积分后可得平行平板间流量计算公式[9]:

(1)

式中，Q为压差Δp作用下流过长度为Δl的平行平板间的流量；h为平行平板间润滑油的油膜厚度；μ为润滑油的黏度；b为平行平板的宽度；v为运动固体壁面对润滑油的剪切速度。

1.3.2流量连续性方程

流量连续性方程为

Qin=Qout

(2)

式(2)表明，流入某个区域或截面的流量Qin应与流出该区域或截面的流量Qout相等。

1.4网格划分及边界条件

按油腔形状将油膜区域进行网格划分，如图2所示。划分好的网格如图3所示。其中，第(i,j)个节点的油膜厚度hi,j为

(3)

式中，θi为Y轴负方向沿逆时针到第(i,j)个节点的圆周角度；h0为初始油膜厚度；ε为偏心率。

图2　网格划分示意图

图3　真实网格图

下面分析边界条件。

(4)

式中，α为小孔流量系数，常取0.6～0.7；dc为节流小孔直径；ρ为润滑油密度。

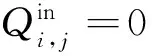
(2)压力边界条件。计算区域边界上的压力为0。

1.5离散格式推导

以图2中的第(i,j)个节点为中心的微元控制体[10-13]作为研究对象(图4)。

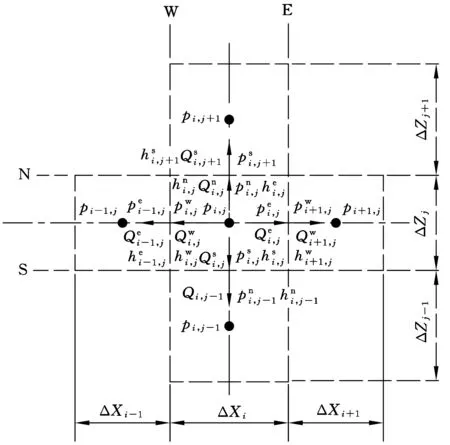
图4　控制体流量平衡图

由平行平板扩散流动方程(式(1))及流量连续性方程(式(2))可知：

(5)

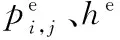
同理可知，在第(i,j)个控制体西侧，有

(6)

在第(i,j)个控制体北侧，有

(7)

在第(i,j)个控制体南侧，有

(8)

(9)

(3)考虑到压力连续性条件，有

(10)

令

求解式(4)～式(10)可得：

(11)

(12)

令

则式(12)可转换为

(13)

采用TDMA迭代法[14-15]求解由式(13)构成的方程组，便可得到整个油腔的压力分布。

1.6轴承承载能力

轴承X、Y方向承载能力FX、FY分别为

(14)

其中，φ为轴承偏位角。为了仿真及计算的方便，仅研究主轴沿竖直向下运动后的承载能力，本文取φ=0。

1.7轴承油膜刚度

Y方向油膜刚度k0为

(15)

式中，eY为Y方向轴心偏移量。

1.8轴承温升

动静压轴承消耗的功率主要包括两部分：泵功耗及剪切摩擦功耗。

根据牛顿摩擦力公式，轴承的剪切摩擦力Ff为

(16)

轴承的剪切摩擦损耗Nf、泵损耗Np分别为

Nf=Ffv

(17)

Np=psQi

(18)

式中，Qi为轴承的总进油量，即4个油腔进油量之和。

轴承温升Δt为

(19)

式中，cV为润滑油的质量热容，取2120 J/(kg·K)。

2　基于有限体积法的承载特性分析

2.1初选轴承结构参数及供油参数

在理论分析时，初选的轴承结构参数及供油参数见表1。研究承载特性时，除所研究参数外，其余参数按表1选取。

表1　初选轴承结构参数及供油参数

2.2求解结果

在图5中，深腔区域的油腔压力为均匀分布。静止时在圆周方向，油膜压力从深腔到浅腔逐渐减小，在浅腔末端压力达到最小(图5a)；工作时在圆周方向，油膜压力从深腔到浅腔逐渐增大，在浅腔末端压力达到最大(图5b)；在轴向，从中间向两端压力逐渐减小。

2.3承载特性分析

2.3.1供油压力的影响

动静压轴承是依据供油产生的静压效应及一定转速下楔形油膜的动压效应工作的。在使用过程中，轴承的结构参数是确定的，则供油压力成为制约轴承性能的关键工作参数。当供油压力为1.5～4.0 MPa时，承载能力、油膜刚度、进油流量和温升随偏心率ε的变化规律如图6所示。

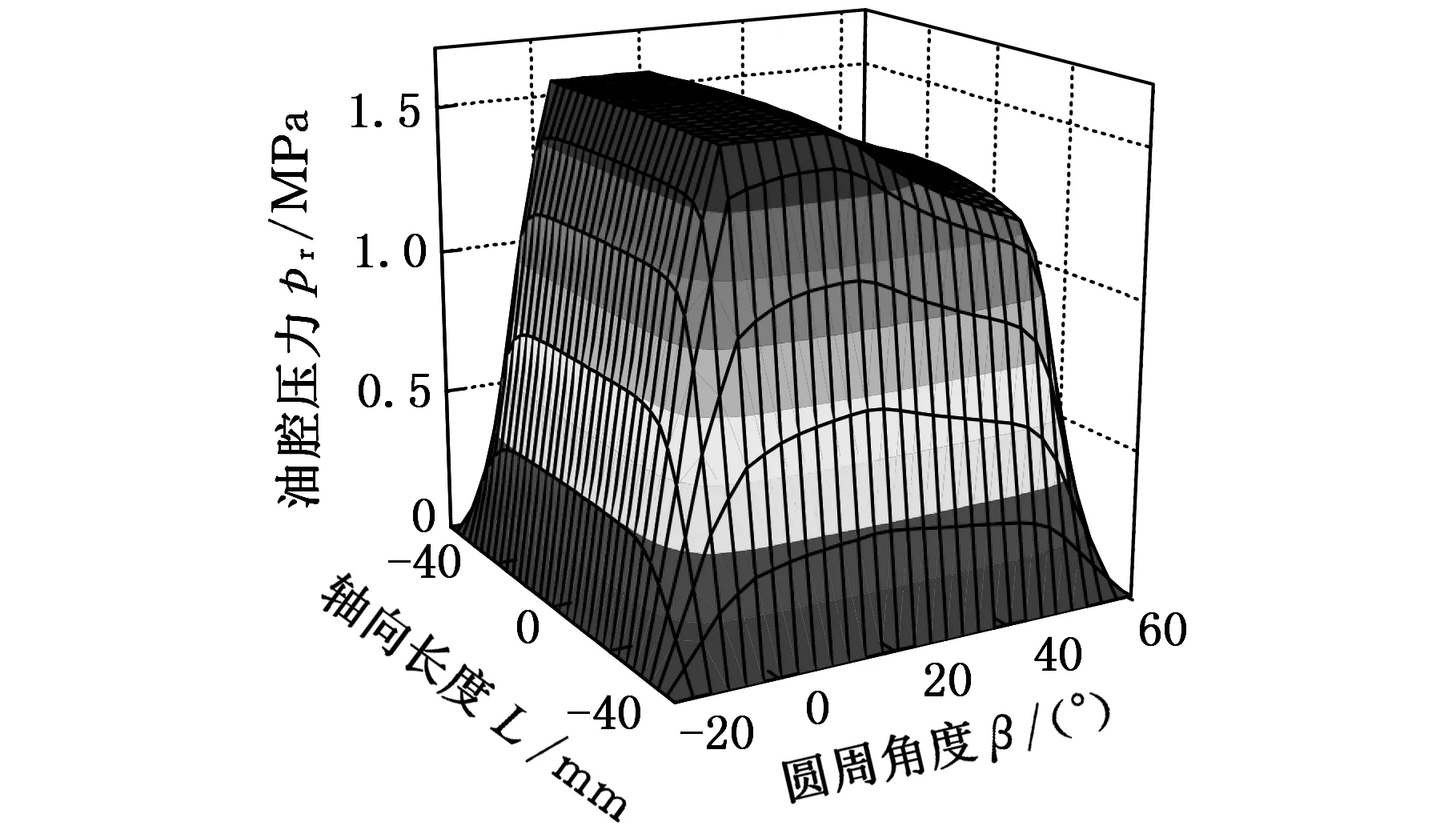
(a)转速为0

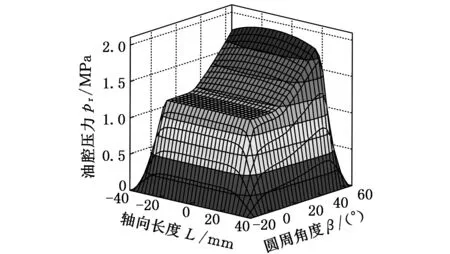
(b)转速为3000 r/min图5　第一油腔压力分布图

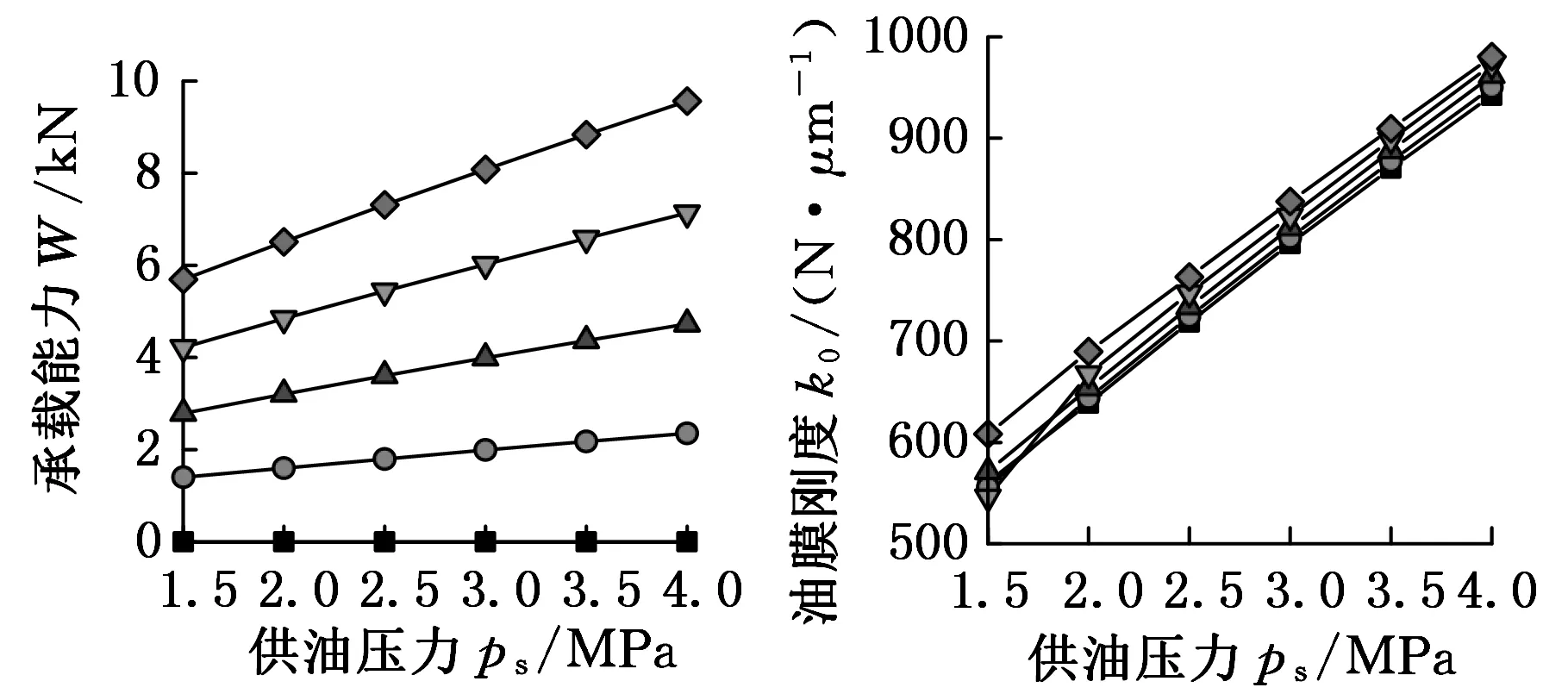
(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图6　供油压力对承载特性的影响

由图6可知，当偏心率一定时，承载能力、油膜刚度及进油流量均随供油压力的增大而增大，而温升却随供油压力的增大而减小。这表明增大供油压力对提高轴承的承载特性是有利的，但是供油压力越大，越易导致进油管道的泄漏。因此，在保证足够的刚度、承载能力及温升条件时，供油压力取2.5～3.5 MPa较为合适。

2.3.2主轴转速的影响

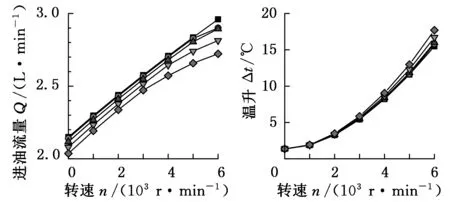
主轴转速是动静压轴承另一个重要的工作参数。高速旋转时产生的动压效应可以提高轴承的刚度。当偏心率为0.1～0.4时，不同主轴转速下，轴承承载能力、油膜刚度、进油流量和温升的变化规律如图7所示。

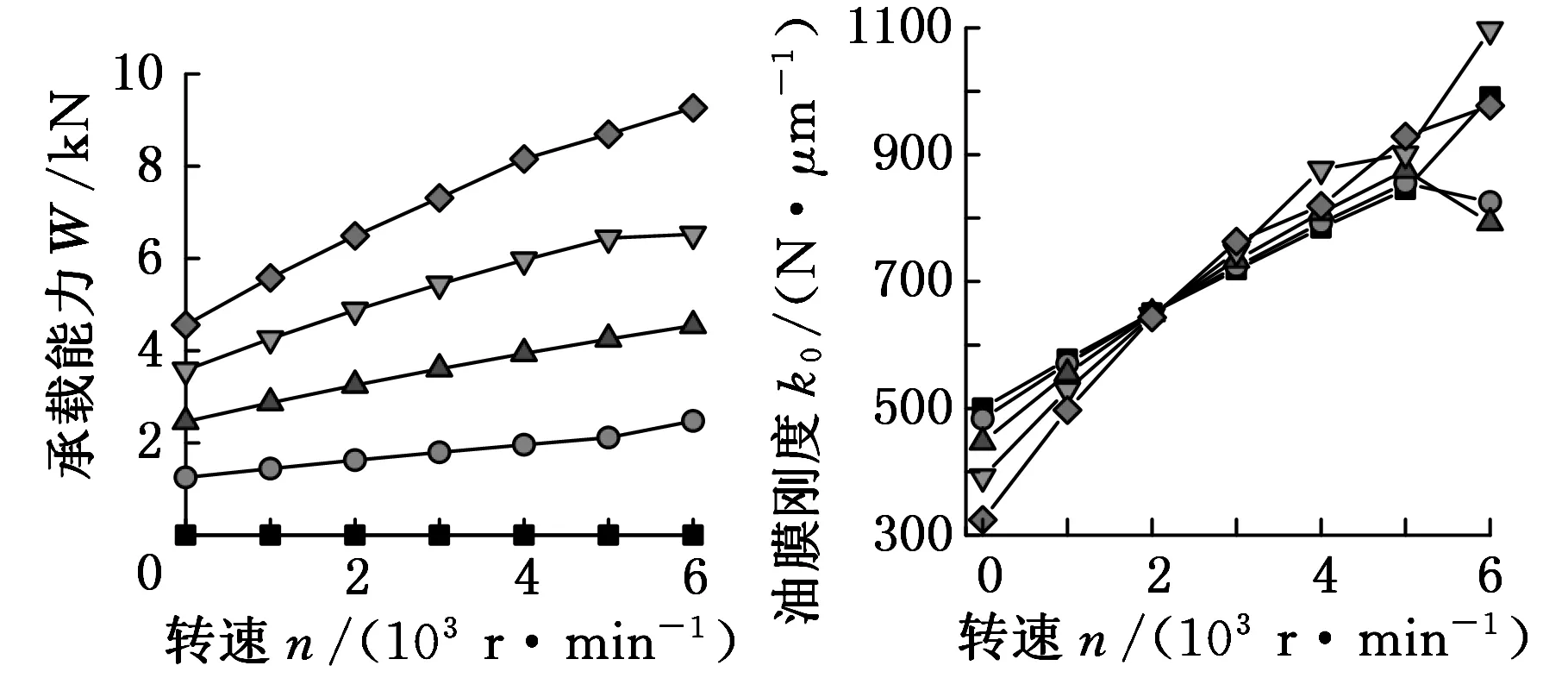
(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图7　主轴转速对承载特性的影响

由图7可知，当偏心率一定时，轴承承载能力、油膜刚度、进油流量及温升均随主轴转速的增加而增大。这是因为，随着主轴转速升高，动压效应增强；深腔压力减小，进油流量增加；剪切摩擦损耗增加导致温升增加。

2.3.3进油孔径的影响

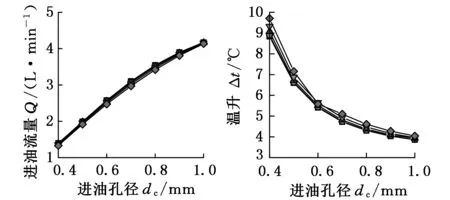
不同偏心率下，进油孔径对轴承承载能力、油膜刚度、进油流量和温升的影响规律如图8所示。

(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图8　进油孔径对承载特性的影响

由图8可知，在某一偏心率下，随着进油孔径增大，承载能力、油膜刚度先增大后减小，进油流量不断增大，温升逐渐降低。这表明随着进油孔径增加，进油流量增大，温升降低。但进油流量越大，回油越困难，越容易造成漏油问题，所以进油孔径不宜过大，取0.6～0.7 mm较为合适。

2.3.4浅腔深度比的影响

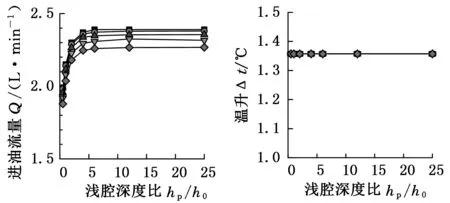
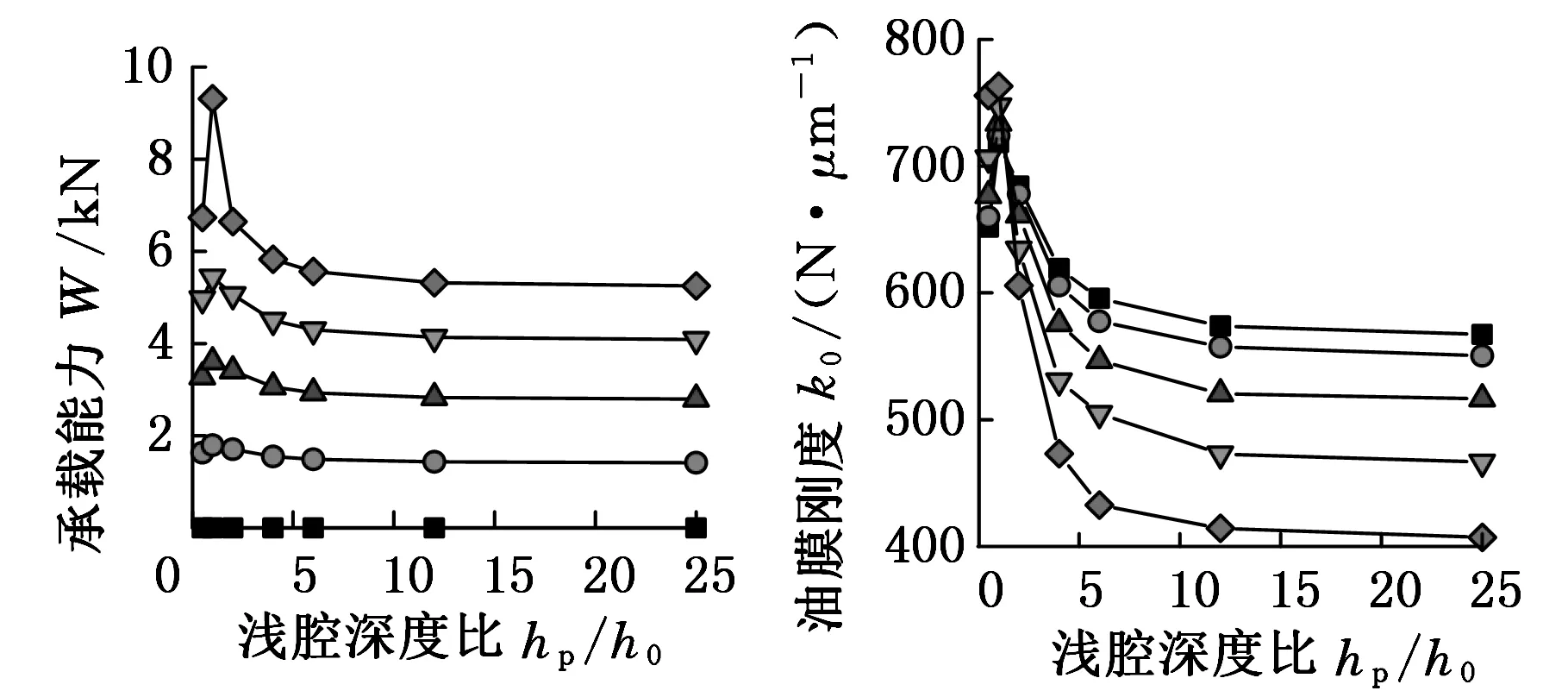
为了增强动压效应，提高动静压轴承的承载能力和刚度，工程上常采用深浅腔的油腔结构。浅腔深度与初始油膜厚度的比值成为衡量浅腔深度大小的重要参数。浅腔深度与初始油膜厚度之比hp/h0分别为0.5、1、2、4、6、12、25时，轴承的承载能力、刚度、进油流量和温升随浅腔深度的变化规律如图9～图11所示。其中，图9～图11的工作转速分别为0、3000、6000 r/min。

在图9中，当转速为0，偏心率ε=0.2，hp/h0从0.5增大至4时，承载能力急剧增至2.78 kN，刚度从365 N/μm急剧增至521 N/μm，流量从1.96 L/min增至2.34 L/min；hp/h0>5后，承载能力、刚度及进油流量趋于平稳。温升不随hp/h0的改变而改变，始终为1.36 ℃。这是因为，在转速为零时轴承不存在动压效应，浅腔深度越大则静压效应越明显；由于不存在速度剪切摩擦损耗，只有泵损耗转化为热量，故温升保持不变。

(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图9　浅腔深度比对承载特性的影响(n=0)

图10　浅腔深度比对承载特性的影响(n=3000 r/min)

图10中，当转速为3000 r/min，偏心率ε=0.2，hp/h0从0.5增大至1时，承载能力从3.28 kN增大至3.61 kN，刚度从676 N/μm增大至734 N/μm，进油流量从2.33 L/min增大至2.55 L/min，温升从6.47 ℃降低至5.52 ℃；当hp/h0继续增大至6时，承载能力减小至2.93 kN，刚度减小至576 N/μm，进油流量减小至2.43 L/min，温升降至4.56 ℃。当hp/h0从10增大至20时，承载特性缓慢减弱。这表明浅腔深度比为2～3时，承载能力、刚度及进油流量最大而温升最小；浅腔深度比大于20时，动压效应几乎消失。为了发挥深浅腔轴承在动压效应作用下增强油膜刚度及降低温升的优势，hp/h0取1～3较为合适。

(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图11　浅腔深度比对承载特性的影响(n=6000 r/min)

2.3.5初始油膜厚度的影响

初始油膜厚度从0.018 mm增大至0.030 mm时(浅腔深度比hp/h0取2)，承载能力、刚度、进油流量和温升随油膜厚度的变化规律如图12所示。

(a)承载能力变化情况(b)油膜刚度变化情况

(c)进油流量变化情况(d)温升变化情况

图12　初始油膜厚度对承载特性的影响

由图12可知，当偏心率一定时，随着初始油膜厚度的增大，承载能力、油膜刚度及温升不断减小，而进油流量逐渐增大。这是因为，随着初始油膜厚度的增加，液阻减小，进油流量增加。流量的增加增强了端泄散热能力，从而引起温升降低。但初始油膜厚度过大，轴承承载能力及刚度过小。因此，初始油膜厚度取0.02～0.03 mm较为合适。

3　结合正交试验法的结构优化设计

通过以上分析，得到了轴承工作参数及结构参数的优选范围，但并未找到使承载特性最优的一组参数。若以承载能力最大、刚度最大、流量最小及温升最低这4个指标为优化目标进行优化计算，则计算量会特别大。众所周知，正交试验法在寻找最优工艺参数时具有减少试验次数的优势[16]。所以，下文借助正交试验法进行理论分析。ε=0.2时，研究初始油膜厚度、浅腔深度比、进油孔径及供油压力4个因素的影响(表2)。

表2　四因素三水平正交试验表(n=6000 r/min)

根据工程经验，动静压轴承的承载特性按照其重要程度依次为温升、刚度、承载能力及供油流量。下面从这4个指标来研究其最优参数组合。

(1)从温升看，最敏感的影响因素为初始油膜厚度h0，最弱的因素为浅腔深度比hp/h0。为使温升最小，较优的因素组合为：ps=3MPa，dc=0.7mm，h0=0.03mm，hp/h0=2。

(2)从刚度及承载能力看，最敏感的影响因素为初始油膜厚度h0，最弱的因素为进油孔直径dc。为使刚度最大，较优的因素组合为：ps=3MPa，dc=0.7mm，h0=0.02mm，hp/h0=1。

(3)从供油流量看，最敏感的影响因素为初始油膜厚度h0，最弱的因素为进油孔直径dc。为使供油流量最小，较优的因素组合为：ps=2MPa，dc=0.6mm，h0=0.02mm，hp/h0=2。

由以上分析可知，4个承载特性指标的优化结果是相互矛盾的，需要根据其重要程度对相关参数做出取舍。因此，最终确定的参数为：ps=3MPa，dc=0.65mm，h0=0.025mm，hp/h0=2。

4　试验分析

4.1试验对象

试验在湖南大学与湖南海捷主轴科技有限公司联合研制的液体悬浮电主轴试验台上进行。该试验台由液体悬浮电主轴(图13)、液压站及JC-3000型冷却器(图14)、电气控制系统(图15)组成。根据所确定的最优参数值，试制了该款电主轴的前后轴承。经配磨加工及塞尺检测，轴承油膜的单边间隙为0.02～0.03 mm。液压站用来提供稳定的供油压力；冷却器用于控制电主轴的进油温度。电气控制系统用于控制该款电主轴在额定频率200 Hz以下实行恒转矩调速，而在额定频率200 Hz以上实行恒功率调速。

图13　液体悬浮电主轴

(a)液压站(b)冷却器图14　液压站与冷却器

图15　电气控制柜与VFD-B型变频器

4.2试验原理

试验原理及压力测试原理如图16及图17所示。按照图16，将电气控制系统、液压冷却系统、液体悬浮电主轴连接在一起。试验时，首先检查电主轴各个元器件及连接系统是否正常工作；然后启动液压系统，检查主轴是否浮起；最后调节电气控制系统，在主轴自重下记录不同转速时前轴承的压力值。如图17所示，在前轴承第2个油腔的浅腔与封油边交汇处钻出一个测压孔，再通过管道把测压孔与压力表相连，试验时直接读取压力表的数值即可。

图16　试验原理图

图17　压力测量原理图

4.3试验及结果讨论

在主轴自重(主轴质量为70 kg)下，当供油压力分别为2.0 MPa、2.5 MPa、3.0 MPa，转速分别为0、2000 r/min、4000 r/min时，油腔压力值见表3。通过理论压力和实测压力的对比，发现轴承浅腔末端处的压力值随供油压力及转速的变化趋势一致，而局部数据点存在一定误差，其中最大相对误差为10.7%。该误差产生的可能原因如下：

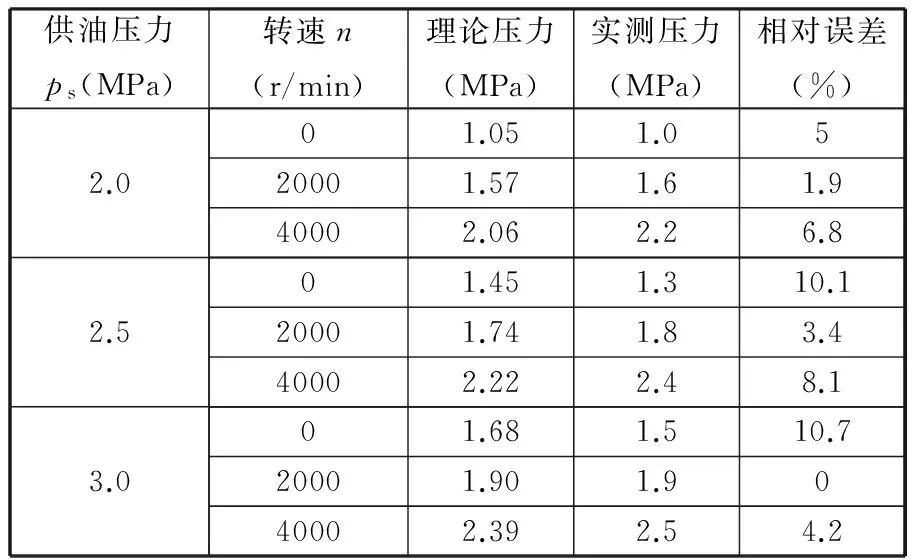
表3　液体悬浮电主轴压力数据表

①由初始油膜厚度的实际值与计算时参数的设定值存在一定差距；②按经验选择的小孔流量系数与实际情况存在一定差距。但就总体趋势而言，理论计算结果与试验测试结果基本吻合。因而该试验在一定程度上验证了优化结果的正确性。

5　结论

(1)基于平行平板扩散流动计算模型及流量守恒原理，推导了微元控制体边界压力的插值函数，建立了分析小孔节流深浅腔动静压轴承的油腔压力、承载力、静刚度、进油流量及温升等承载特性的有限体积计算方法。

(2)定量研究了动静压轴承供油压力、主轴转速、进油孔径、浅腔深度、初始油膜厚度等参数对轴承承载特性的影响规律，进而提出了可增大轴承刚度和降低油膜温升的结构参数及工作参数的优选区域。

(3)采用四因素三水平的正交试验设计方法，在满足多目标性能最优的前提下，理论研究了该轴承结构参数与工作参数的最优组合。最优的一组参数为：ps=3MPa，dc=0.65mm，h0=0.025mm，hp/h0=2。

(4)以最优的组合参数试制了轴承并搭建了试验平台，测量了不同转速及供油压力下油腔的压力值。结果表明，轴承油腔压力的试验数据与计算值能较好地吻合。

[1]武弘毅．动静压轴承讲座：第三讲 动静压混合轴承的结构[J]．机械工人：冷加工，1990(3)：57-62.

Wu Hongyi.Dynamic and Static Pressure Bearing Lecture Ⅲ：Structure of Hydrodynamic and Hydrostatic Journal Bearings[J]．Journal of Mechanical Workers：Cold Work，1990(3)：57-62．

[2]武弘毅，冯明．WMB型动静压混合轴承的基本性能[J]．设备管理与维修，1991(6)：14-16．

Wu Hongyi，Feng Min.WMB Type Hydrostatic and Hydrodynamic Hybrid Bearing[J]．Plant Maintenance Engineering，1991(6)：14-16．[3]Rowe W B．Hydrostatic,Aerostatic and Hybrid Bearing Design[M]．Oxford：Elsevier/ Butterworth-Heinemann，2012.[4]熊万里，阳雪冰，吕浪，等．液体动静压电主轴关键技术综述[J]．机械工程学报，2009，45(9)：1-18．

Xiong Wanli，Yang Xuebing，Lü Lang，et al．Review on Key Technology of Hydrodynamic and Hydrostatic High-frequency Motor Spindles[J].Journal of Mechanical Engineering，2009，45(9)：1-18．

[5]孙恭寿，冯明．液体动静压混合轴承设计[M].北京：世界图书出版公司，1989.

[6]郭胜安，侯志泉，熊万里，等．基于CFD的深浅腔液体动静压轴承承载特性研究[J]．制造技术与机床，2012(9)：57-61.

Guo Sheng’an，Hou Zhiquan，Xiong Wangli, et al．Bearing Characteristics Study on Liquid Hybrid Bearing Based on CFD[J]．Journal of Technology and Machine Tool，2012(9)：57-61.

[7]Wang Lin, Pei Shiyuan，Xiong Xianzhi．Study on Static Performance and Stability of a Water-lubricated Hybrid Bearing with Circumferential Grooves and Stepped Recesses Considering the Influence of Recess Sizes[J]．Tribology Transactions，2014，57(1)：36-45.

[8]许尚贤.液体静压和动静压滑动轴承设计[M].南京：东南大学出版社，1989.

[9]陈燕生.液体静压支承原理和设计[M]．北京：国防工业出版社，1989.

[10]帕坦卡S V．传热与流体流动的数值计算[M]．朱彤，译．北京：科学出版社，1984．

[11]张直明．滑动轴承的流体动力润滑理论[M]．北京：高等教育出版社，1986.

[12]Arghir M，Alsayed A，Nicolas D.The Finite Volume Solution of the Reynolds Equation of Lubrication with Film Discontinuities[J].International Journal of Mechanical Sciences，2002，44(10)：2119-2132．

[13]张俊红，李周裕，何振鹏，等．空穴效应对倾斜轴颈轴承润滑性能影响的研究[J].中国机械工程，2013，24(21)：2913-2920.

Zhang Junhong，Li Zhouyu，He Zhenpeng，et al.Reserch on Cavitation Effect on Lubrication Performance for Misaligned Journal Bearings[J]. China Mechanical Engineering, 2013，24(21)：2913-2920.

[14]陶文铨.数值传热学[M].2版.西安:西安交通大学出版社，2001.

[15]李人宪.有限体积法基础[M].北京：国防工业出版社，2008.[16]刘振学，黄仁和，田爱民.实验设计与数据处理[M]. 北京：化学工业出版社，2005.

(编辑陈勇)

Structure Optimization Design of Hydrostatic-dynamic Journal Combined Finite Volume Method with Orthogonal Experimental Design Method

Meng Shuguang1Xiong Wanli1Wang Shaoli1Lü Lang1Zheng Lianggang2

1.National Engineering Research Center for High Efficiency Grinding,Hunan University,Changsha,410082 2.Hunan Haijie Spindle Technology Co., Ltd.,Changsha,410082

Due to the problem of operating performance optimization of hydrodynamic-static hybrid journal with orifice restrictor, based on the calculation model of parallel plate diffusion flow and the principles of flow conservation,a interpolation function of the boundary pressure for the micro control volume was derived.A method belonged to the finite volume method was proposed to calculate the characteristics for a kind of deep-shallow recess bearing,including load capacity,bearing stiffness,flow rate and temperature ascending relationship.The method was used to study bearing characteristics with different structure parameters and working parameters,such as supply pressure，spindle speed,oil inlet aperture,shallow depth and initial oil film thickness.Then,the optimization ranges of the above parameters were obtained. Under the preconditions of satisfying multi-objective optimization,the optimal combination of the structural parameters and operating parameters of the bearing was deduced, using a orthogonal experimental design method which named four factors three levels.The deep-shallow bearings with orifice restrictors were trial by the optimal parameters, and an experimental platform was established. The pressure values of oil cavity were measured with different rotational speed and supplying pressure. The results show that the trend of experimental data and numerical simulation results for spindle speed are consistent, and the error is within 11%. The reliability of the structure optimization design method for the deep-shallow bearings with orifice restrictors is verified, which combines the finite volume method with orthogonal experimental method.

finite volume method;orthogonal experimental design method;orifice restrictor;deep-shallow hydrodynamic-static hybrid journal bearing;load characteristics;structure optimization design

2015-04-08

国家自然科学基金资助项目(51275163)；湖南省自然科学杰出青年基金资助项目(12JJ1006)

TH133.31

10.3969/j.issn.1004-132X.2016.09.016

孟曙光，男，1983年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为液体静压轴承技术及转子系统动力学。熊万里(通信作者)，男，1971年生。湖南大学机械与运载工程学院教授、博士研究生导师。王少力，男，1981年生。湖南大学机械与运载工程学院博士研究生。吕浪，男，1979年生。湖南大学机械与运载工程学院讲师。郑良钢，男，1987年生。湖南海捷主轴科技有限公司工程师。